The search for bio markers of disease have moved from metabolites to proteins and to genes and back again as technology which was developed. Bio-analytical scientists have been trained for decades to methodically isolate, identify and measure specific molecules. Rapid separations coupled to mind blowing rapid mass spectral characterization and generating analytical profiles within minutes which contain incomprehensible amounts of data. As the old saying goes we “can’t see the wood for the trees”. The realization is that in this data rich age we no longer have to methodically isolate characterize and measure specific molecules. What is important is to identify which of the 100’s or 1000’s of resolved and measured “unknown” molecules is associated with the pathology for which we are interested. The goal is markers of clinical relevance and statistical examination of patterns of association is the new mantra of the biomedical analyst - so called shotgun analysis. However, as any clinical biomedical scientist will tell you; a biomarker has to be robust, easily, rapidly and cheaply measured if it is to be adopted in a hospital laboratory. Any shotgun analysis has to recognize these constraints and not just identify statistical outliers that are seen only sometimes in a few samples and not consistently in the majority of the pathology in question. We have applied the SIMCA P+ plus software in shotgun metabolomic analysis of pregnancy urine.

Any metabolomics analysis generates vast amount of data which can rarely be manually handled completely or without the need of statistical analysis. The spectra recorded using technologies MS are highly multivariate, influenced by a large number of variables. It is essential to use multivariate analytical methods to analyse such data. A typical MS spectrum consists of mass to charge ratios of analysed compounds or their fragments over the time. The use of traditional statistical methods is not as popular as multivariate analysis because of the large range of underlying variables. The data becomes further complex when these technologies are coupled to separation technologies like chromatography. For instance combinations like MS-MS, Gas chromatography -MS, Liquid Chromatography -MS, Gas Chromatography-NMR and Liquid Chromatography -NMR are bound to generate data with one or more dimensions per observation, from vectors up to multi-way arrays.

Thus, when coupled to separation instruments one or more retention time dimensions are added to the series of mass spectra. By integration of MS dimensions, it is possible to obtain a total ion chromatogram (TIC) but the information in the individual MS dimensions is of core importance for profiling studies. The UV chromatogram and mass spectrometer’s total ion count are obtained in form of a graph. The UV chromatogram generated shows the peaks at particular retention time. Each of these could represent more than one underlying analytes. The ions at any particular retention time can be studied in both positive and negative mode. However, for complex samples where unknown numbers of analytes are present, an unknown number of ions are generated at particular retention time. This makes it difficult to definitely predict what particular ion causes the elevation in total ion count. Hence, external profiling software can be used which extracts all the graphical chromatogram into a numerical matrix.

In order to carry out statistical analysis, mass spectrometry data has to be exported to third party software. For Shimadzu instruments this is achieved by transforming the total ion chromatograms into numerical version by using Profiling Solutions® software (Shimadzu, UK). The time-aligned high mass accuracy MS data can be exported as aligned matrix to Umetrics SIMCA P+ (Umeå, Sweden). All the data is scaled and mean-centred in order to standardize the coefficients when exported to SIMCA P+. Thus, the means are subtracted from all values for standardisation of the data after it is extracted. All positive as well as negative ions are included for this transformation.

In order to control the bin width when identifying centroid ions, an ion m/z tolerance needs to be set and we have used to +/- 25 mDa. It was found that the ion mass accuracy is not affected if wider tolerance is used. The retention time alignment of ions across the data set is limited to 0.2 min in order separate isomer peaks (if any) with at least 0.2 min retention difference. The ion intensity threshold of 20,000 is often set in order to reduce background noise, so that centroid intensities below 20,000 were not included in the data. To reduce interference from background noise a retention time window is set for extraction. As described in our accompanying paper in this issues on the development of a ZIC HILIC MS separation method for urinary metabolomics (Editor: REF from Journal), during method and software validation experiments QC samples are injected before and after the sample analysis in order to check reproducibility. The QC samples contained representative pool of all the samples in that particular experiment. Thus, during data pre-treatment only 70%+ of the total pooled QC ions are included in the extracted data matrix. Percentage of relative standard deviation in ion response and retention time shift is set to 15% and 5% respectively. A two-column file matrix is hence generated for each sample which contains all the ions detected at various retention times throughout the whole data file. The matrix contains values of highest intensities found at a particular retention time for a specific m/z and these values are represented in form of heat map with colours (Figure 1).

Figure 1: Ion matrix generated using profiling solutions software after data treatment for noise reduction shows extracted significant m/z values at particular retention time. The columns shows intensity of all the significant ions extracted for any particular sample whereas the rows represent intensities of a particular m/z at definite RT for each sample.

In order to study complex metabolomics data, pre-processing and pre-treatment of the data is required. Ebbels Cavill R suggested that data pre-processing for NMR includes phasing of Fourier transforms and de-convolution of overlapping metabolites in LC-MS/GC-MS when extracting the data for analysis [1]. The data pre-treatment is referred to as normalisation, scaling, or baseline correction (and any other methods that are required to make the samples comparable to each other); however in chemometrics and applied statistics, pre-processing implies over all data processing that makes the data suitable for statistical analysis [2]. A typical MS or NMR spectrum generates thousands of variables per sample and when considering a large study, thousands of variables within thousands of samples, becomes extremely difficult to analyse without multivariate analysis. For metabolomics study, the bilinear factor models that are most commonly cited are principle component analysis (PCA) and partial least square discriminant analysis (PLS-DA). Bilinear factor models are specially designed to overcome dimensionality problems and take advantage of co-linearity of the data by compressing single components and pseudo variables in the form of weighted linear combination of the original data [2]. The ion matrix can be exported in ASCII format such that X variables are the ion responses in order to carry out multivariate analysis using third party statistical analysis software like SIMCA P+. SIMCA P+ is multivariate analysis software that uses soft independent modelling of class analogies (SIMCA). SIMCA is a classification method constructing separate PCA and PLS-DA models for each group enabling categorization of samples into groups. In SIMCA P+ ion m/z and RT are selected as primary and secondary variable IDs respectively in order to carry out multivariate analysis e.g. PCA or PLS.

PCA is unsupervised multivariate analysis where the modeling does not involve any user intervention and is based only on the explanatory variables leaving any responses optional for later stages of data analysis. PLS-DA on the other hand is a supervised analysis where the user can predefine the groups within the samples in order to see how the underlying variables affect the separation between two groups i.e. if there is any change in the mean ion intensities, if there is any change in the absence or presence of variables etc. PCA identifies groups of variables which are inter-related but not directly noticeable (Figure 2). PCA assumes that any observed variables somehow correlate with small number of underlying variables or latent variables. The observed correlation matrix then can manifest variables aiming to highlight the underlying latent principle components. The first principle component (PC1) shows factor that explains maximum variation in the dataset by creating a line that passes through all the variables with minimum possible distance using the least-sum-of-squares technique. The second principle component (PC2) shows maximum variation that is not explained by PC1 alone and is generated by drawing a perpendicular line across first line at the point where maximum data is concentrated. This process is repeated until the number of principle components is equal to the number of variables in the dataset in the n-dimensional space. The multiple correlations in PCA are explained by eigenvalues.

Figure 2: An example of a typical PCA plot based on real data where paracetamol has been spiked into a normal human urine samples. The spiked and non-spiked samples were analysed blind on the Shimadzu Trap-ToF MS, data processed using Shimadzu Profiling Solutions and exported to SIMCA P+ for multivariate analysis. Two clusters were identified where among the 12,000+ ions (pre-extraction of noise and variable ions) which matched the partition of the samples precisely to spiked and un-spiked urine: the differentiation being the presence of m/z ions and retention characteristics corresponding to paracetamol.

Mathematically it can be expressed that,

Av00=λ v

Where A is square matrix,

v is non-zero vector and is eigenvector of A

λ is a scalar vector and eigenvalue of A that corresponds to v.

In PCA, it’s assumed that the manifest variables cluster around a particular line and their eigenvalues increase owing to the eigenvalues of other principle components. Thus, variation due to a given principle component can be explained as its eigenvalue divided by the number of manifest variables in the analysis. For example, if in a PCA analysis there are two variables only – A and B and each have an eigenvalue of 1, the sum of their eigenvalues will be 2. The data points will cluster around a perpendicular line representing PC1. The total length of PC1 vector from centre of data cluster to its edge along PC1 represents the eigenvalue of PC1. If the variables in the data cluster are associated with each individual (i.e. eigenvalues=1) then the length of PC1 will be greater than 1. The line perpendicular to PC1 will represent PC2 and is expected to have eigenvalue of less than 1. In this case since there are just two variables, PC1 (eigenvalue>1) represents the maximum variability associated with the data set.

Using SIMCA P+ once the data set is imported, a default work set is created. The default work set consists of all the observations (in the current work described in the accompanying paper, m/z values and their RT) in the primary data set with all the variables (in the current work intensities) scaled to unit variance and defined as X’s (for PCA-X) and Y’s (for PLS-DA). The model built using SIMCA P+ generates a summary of fit of the model which includes: A (number of components), N (number of observations in the model), R²X (cumulative X-variation modelled after A components), R²Y (cumulative Y-variation modelled after A components (PLS)), Q² (cum) (cumulative overall crossvalidated R²X for as PC model R²Y for a PLS model). R²X represents fraction of the variation of the data explained by each component, R²X (cum) represents cumulative of R²X. The variables are correlated and summarised by two new variables t1 and t2 scores whose values explain the variation represented by each principle component. The scores t1 and t2 are orthogonal, i.e., completely independent of each other. There are as many scores as components in the model. The score t1 (first component) explains the largest variation of the X space, followed by t2, etc. Hence, the scatter plot of t1 vs. t2 is a window in the X space, displaying how the X observations are situated with respect to each other. This plot shows the possible presence of outliers, groups, similarities and other patterns in the data. The score plot is a map of the observations. With a two-dimensional score plot, SIMCA-P+ draws the tolerance ellipse based on Hotelling’s Tand summarised by two new variables t1 and t2 scores whose values explain the variation represented by each principle component. The scores t1 and t2 are orthogonal, i.e., completely independent of each other. There are as many scores as components in the model. The score t1 (first component) explains the largest variation of the X space, followed by t2, etc. Hence, the scatter plot of t1 vs. t2 is a window in the X space, displaying how the X observations are situated with respect to each other. This plot shows the possible presence of outliers, groups, similarities and other patterns in the data. The score plot is a map of the observations. With a two-dimensional score plot, SIMCA-P+ draws the tolerance ellipse based on Hotelling’s Tand summarised by two new variables t1 and t2 scores whose values explain the variation represented by each principle component. The scores t1 and t2 are orthogonal, i.e., completely independent of each other. There are as many scores as components in the model. The score t1 (first component) explains the largest variation of the X space, followed by t2, etc. Hence, the scatter plot of t1 vs. t2 is a window in the X space, displaying how the X observations are situated with respect to each other. This plot shows the possible presence of outliers, groups, similarities and other patterns in the data. The score plot is a map of the observations. With a two-dimensional score plot, SIMCA-P+ draws the tolerance ellipse based on Hotelling’s T² (95% tolerance was set for all the data analysis during this research). Observations situated outside the ellipse are outliers. If the score plot shows groups it is advisable to understand the differences between the groups by doing a SIMCA classification or a PLS-DA. When one is interested in relationship with the responses Y (PLS), it is advisable to fit a different PLS model for each group. (95% tolerance was set for all the data analysis during this research). Observations situated outside the ellipse are outliers. If the score plot shows groups it is advisable to understand the differences between the groups by doing a SIMCA classification or a PLS-DA. When one is interested in relationship with the responses Y (PLS), it is advisable to fit a different PLS model for each group. (95% tolerance was set for all the data analysis during this research). Observations situated outside the ellipse are outliers. If the score plot shows groups it is advisable to understand the differences between the groups by doing a SIMCA classification or a PLS-DA. When one is interested in relationship with the responses Y (PLS), it is advisable to fit a different PLS model for each group.

A good visual check on what might be driving the PCA and or PLS plots is to generate a loading plot. This where all variables i.e. RT and ions, measured are plotted on the same axis diagram as the PCA/PLS plot. Thus a particular variable (i.e. RT and ion m/z) can be seen to be overlaid in a corresponding quadrant to which the group of observation (i.e. representative urine sample) has been isolated (Figure 3).

Figure 3: An example of a typical loading plot. This plot shows m/z values for urine samples spiked and un-spiked with crushed paracetamol tablets (1mM to 1fM concentrations). The m/z values plotted here can be overlaid with the corresponding quadrants of PCA plot shown in figure 2. The m/z value of paracetamol detected negative ion mode is indicated with red circle which corresponds to the quadrant in which majority of paracetomol spike urine samples were observed on the PCA plot (see figure 2).

Orthogonal partial least squares discriminant analysis (OPLS-DA) is a multivariate regression method used for extracting systematic variations e.g. batch order, drift in the system etc. from the variables related to specific responses e.g. from diseases, from drug intake etc. In OPLS-DA analysis a response is generated based on dummy variables holding information about the classes in which samples are distinguished. Wuolikainen et al. (2012) have demonstrated successful use of OPLS-DA analysis model, followed by cross validation of the model for metabolomics profiling of cerebrospinal fluid in amyotrophic lateral sclerosis [3].

The statistical models thus, created however, do not always stand true as predictive models unless validation of the model has been carried out. Without validation, there is always an associated risk of over-fitting the data. Such over-fitted data stands out to be unreliable if considered for any clinical situations. Two main approaches to model validation in multivariate statistics are test-set validation and cross validation. Test-set validation uses a separate data set from the one used for the study in order to validate the multivariate model. By keeping the test data separate from the calibration process the validation reveals reproducibility and the accuracy of the models. However, for metabolomics chemometrics cross-validation splits the actual experimental data into equally-sized blocks and can use different combinations (permutations) for create a permuted response which is then compared with the real/original response.

Randomization-based validation techniques like bootstrapping and permutation tests are useful means of validating multivariate statistical models. Bootstrapping involves sampling with replacements from a non-parametric dataset or adding random noise to known data set in order to estimate the underlying distribution. However, permutation testing where no additional data or noise is added to the raw data is more useful way of approaching model validation as the observations are disconnected from their responses to analyze if the observed statistics is significantly better than it would be using random relations. The permutation tests can also be generalized using rotational tests where the data is randomly rotated on the covariance matrix. The covariance structure of the data is maintained by doing this rotation and is beneficial for a small set of data.

The VIP score algorithms in the SIMCA P+ software is copyright protected. Although the working of VIP score is known, the algorithm is not revealed. VIP plot is type of a coefficients plot which summarizes the relationship between the Y variables and the X variables. These coefficients are directly analogous to the coefficients obtained from multiple regression but they are not identical. The VIP plot describes which X variables characterize the X block well and which variables also correlate with Y. Thus, VIP value will summarize the overall contribution of each X-variable, summed over all other components and weighted according to the Y variation accounted for by each component.

This VIP score is a critically important check on the selection of significant ions in a complex data set from metabolomics. The PLS and PCA plots are used to visually select candidate ions that are significantly distant from the mean (represented by the central intercept of the axes) and from each other. The higher the VIP score (greater than 1) the more significant is the ion in complex analysis in comparing the difference between two or more groups (Figure 4). Thus PLS and PCA selected analyte groups or single analyte ions can be confirmed by the VIP scores as truly significant.

Figure 4: An example of a typical SIMCA P+ variable plot (VIP). This example has ranked all the variable m/z ions that differentiated between the urine samples spiked or un-spiked with paracetamol. An analysis revealed that paracetamol, its conjugates and formulation components of paracetamol tablets were ranked at VIP score of more than 1 (highlighted in red circle). These ions represent (the biomarker) analytes distinguishing between two groups using shotgun analysis.

However, the VIP score is slightly “black box” analysis. In order to demystify VIP we discovered that this approximates to z-scores. When the data is not normally distributed, an approximation for its standard normal distribution can be made using z-scores. It is calculated based on the following formula:

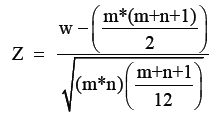
Where, m, n=number of samples in two groups.

W=Mann-Whitney score for the non-normally distributed data

A z-score can be positive or negative and generally +/- 2 represent a significant variation. The VIP score appears to be an algorithm that incorporates z-scores and other factors such the number of times an ion is detected, the median ion intensity and deviation from the median.

Whatever the true relationship, VIP represents a valuable component in complex shotgun analysis of the metabolome in selecting unknowns from multiple potential analytes that should be measured as biomarkers.

In conclusion, overwhelmingly complex and information rich mass spectral information can be extracted and transformed into numerical matrices that can be explored further using multivariate analysis software such as SIMCA P+. The multivariate analysis using third party software gives an overview of the mass spectral data; regression analysis and non parametric statistical methodology can avoid bias cherry picking of data and help selection of the significant biomarker analyte(s).