Journal of Clinical Trials
Open Access

Investigating Synthetic Controls with Randomized Clinical Trial Data in Rheumatoid Arthritis Studies

Author info »

Introduction

There has been a growing interest in using external control data to estimate the effects of treatments on outcomes, collectively known as synthetic control methods [1]. Synthetic control provides a way to save time and cost in clinical trials for drug development [2]. When a synthetic placebo arm is considered to replace the actual placebo arm from a clinical trial, it would not only greatly encourage patients to attend the study because of an increased chance to receive an active study drug instead of placebo, but also make the trial more ethical [3]. While Randomized Clinical Trials (RCTs) are very powerful and stand as an almost sacred principle, synthetic control could serve as a supplement to RCTs for the cases where patient-level historical control data or real-word data are available and bias could be reasonably controlled is a viral illness that remains a lethal pandemic. Instead of recruiting “real” patients to the control group, a synthetic control group can be created from patientlevel historical clinical trial data or real-world data with similar settings by looking for subject characteristics that approximately match patients recruited in the investigational drug group. Such data can be used to reduce or completely replace a concurrent control arm. However, caveats have been raised for the interpretability of trial results when there is a difference between concurrent control and historical control. With this concern, using such external-trial data or historical clinical trial data has been limited to exploratory trials, rare diseases, or pediatric trials, despite its routine use in development of medical devices.

Beyond the patient-level synthetic control arm, there are many discussions in literatures regarding using historical data based on a Bayesian approach where group-level data are used as prior information in clinical trial design and analysis. Pocock [4] proposed a method accounting for the difference between current and historical data. The difference is treated as a random variable. Neuenschwander et al. [5] described a Meta-Analytic- Predictive (MAP) method to account for the heterogeneity between historical data and current data and determine the effective sample size from historical data to interpret borrowed information, which is very helpful in communicating the borrowing results to non-statisticians. Schmidli et al. [6] extended MAP by introducing a mixed prior with a robust component to summarize historical data information. Ibrahim and Chen [7], Duan et al. [8] and Neuenschwander et al. [9] presented the power prior and the modified power prior methods to downweigh the information in the historical data. Hobbs et al. [10] established the commensurate prior for generalized linear mixed model and Murray et al. [11] extended it to piecewise exponential survival distribution. One common challenge for Bayesian approaches is the interpretation of prior information summarized from group-level external data, which would not incorporate patient-level information and baseline characteristics into the analysis.

Comparing to the Bayesian approach, the purpose of propensity score methods is to improve the accuracy of treatment effect estimates by matching relevant covariates with patient-level data [12]. In a simple two-arm RCT with 1:1 ratio to compare an investigational drug and placebo, the probability of a subject being exposed to the investigational drug is 50%. Although any pair of subjects could have different characteristics, the overall characteristics should be expected to be balanced from randomization. Therefore, the estimated treatment effect (the difference of the outcomes between two groups) is an unbiased estimate. The propensity score is defined as the conditional probability of a subject being assigned to the treatment group given the observed covariates. Rosenbaum and Rubin [13] demonstrated that the observed covariates are balanced at each value of the propensity score. Hence one could essentially view those with similar propensity score as a random sample of all subjects.

Propensity score methods have been used with increasing frequency to estimate treatment effects in observational studies. Austin [14] described how propensity score methods could be used to reduce or eliminate the effects of confounding when using the observational data to estimate treatment effects. In recent advanced clinical research, propensity score methods, particularly the propensity score matching methods, are applied to select additional control group subjects from external data to maintain a balanced randomization between treatment group and control group [2]. Moreover, for a single-arm clinical study without a control group, propensity-score-based methods could be used to create a synthetic control arm from either historical trial data or external real-world data. This process mimics randomization to create two treatment groups with comparable characteristics, hence the treatment effect could be estimated between the investigational drug group in the study and the synthetic control group from external data.

There are many discussions of using a propensity score method to create a synthetic control arm. Recently in a “Friends of Cancer Research” white paper, Davi et al. [15] compared the concurrent control arm in a randomized non-small cell lung cancer study with the synthetic control arm created from control arms in other randomized trials. In particular the synthetic control arm was chosen to match the concurrent control arm based on propensity score matching approach which successfully balanced the distribution of baseline characteristics between the two control arms. Most recently, Schwartz and Ries [16] proposed a comparison between a propensity score matched observational study and a randomized control trial. To our knowledge, there is no published literature illustrating constructing a synthetic control arm from other randomized trials to match the active treatment arm in the real randomized trial and then performing corresponding analysis of the treatment effect vs. the synthetic control arm using the propensity-score-based methods.

In this paper, we choose a real randomized rheumatoid arthritis trial with both treatment and placebo arms as a target trial, and the treatment effects estimated from this trial is considered as the benchmark. Synthetic control arms are then constructed from the placebo arms of other randomized RA trials to match the treatment arm in the target trial using four different propensity-score-based methods. The treatment effects estimated between the treatment arm and the synthetic control arms are compared with the benchmark to check the accuracy for different propensity score analysis methods. Our purpose is to demonstrate the feasibility of utilizing real randomized trial data to establish a synthetic control arm using propensity-score-based methods in new drug development. Our analyses show that such a synthetic control arm constructed from real randomized trial data could improve the trial efficiency while saving time and cost in new drug development.

The manuscript is organized as follows. In randomized rheumatoid arthritis clinical trials, we describe the randomized rheumatoid arthritis clinical trials considered as the target trial and as the external clinical trials for creating synthetic control arms. Propensity score methods presents propensity-score-based synthetic control analysis methods. Results illustrate analysis results for each method followed by the discussions.

Materials and Methods

Randomized rheumatoid arthritis clinical trials

AbbVie Study BALANCE-1 (NCT01960855) [17] is a Phase II, randomized, double-blind, parallel-group, placebo-controlled multicenter study comparing the safety and efficacy of multiple doses of upadacitinib versus placebo administered for 12 weeks in subjects with moderately to severely active rheumatoid arthritis who have shown an inadequate response or intolerance to anti-TNF biologic therapy. Subjects who met eligibility criteria were randomized in a 1:1:1:1:1 ratio to 1 of the 5 treatment arms: upadacitinib 3 mg BID (N=55), 6 mg BID (N=55), 12 mg BID (N=55), 18 mg BID (N=55) and Placebo (N=56).

AbbVie Study SELECT-BEYOND (NCT02706847) [18] is a Phase III multicenter study that includes a placebo controlled period (Period 1) and long-term extension period (Period 2). Only period 1 will be discussed here, which is a 12-week, randomized, double-blind, parallel-group, placebo-controlled period designed to compare the safety and efficacy of upadacitinib 30 mg QD and 15 mg QD versus placebo for the treatment of signs and symptoms of subjects with moderately to severely active rheumatoid arthritis who are on a stable dose of csDMARDs and had an inadequate response to or intolerance to at least 1 bDMARD.

Subjects who met eligibility criteria were randomized in a 2:2:1:1 ratio to one of four treatment groups: upadacitinib 30 mg QD (N=165); upadacitinib 15 mg QD (N=165); and Placebo1 (N=84) (Day 1 to Week 12) → upadacitinib 30 mg QD (Week 12 and thereafter); and Placebo (N=85) (Day 1 to Week 12) → upadacitinib 15 mg QD (Week 12 and thereafter). For Week 12 analysis in this paper, total placebo (N=169) will be combined as the placebo group from study SELECT-BEYOND.

The primary endpoint for both studies is American College Rheumatology 20 (ACR20) response (improvement of 20% in ACR criteria) at Week 12.

The main inclusion and exclusion criteria for both studies are similar as shown below and hence these two studies are comparable.

Main inclusion

• Adult male or female, at least 18 years old.

• Diagnosed with RA for ≥ 3 months.

• Subjects must have been receiving oral or parenteral MTX therapy (for BALANCE-1 study) or csDMARD therapy (for SELECT-BEYOND study) ≥ 3 months.

• Subjects have been treated with at least 1 bDMARD for ≥ 3 months but continue to exhibit active RA, or had to discontinue due to intolerability or toxicity.

• Have active RA as defined by the following minimum disease activity criteria.

a) ≥ 6 swollen joints (based on 66 joint counts) at Screening and Baseline Visits.

b) ≥ 6 tender joints (based on 68 joint counts) at Screening and Baseline Visits.

c) hsCRP ≥ 3 mg/L at Screening Visit.

Main exclusion

A subject was excluded from both studies if he/she meets any of the following criteria.

1. Prior exposure to JAK inhibitor (e.g., tofacitinib, baricitinib).

2. Screening laboratory values meeting the criteria for the corresponding studies as in Table 1 below.

Table 1: Exclusion criteria for screening laboratory values.

To illustrate the propensity-score-based synthetic controls and evaluate results from different methods, we consider SELECT-BEYOND placebo group as external control data and one of BALANCE-1 active treatment groups-upadacitinib 6 mg BID treatment group (54 subjects) as the in-trial treatment group. Propensity score analysis methods are applied in these data to assess the treatment effect of upadacitinib in comparison with placebo for ACR response at Week 12. The placebo group in study BALANCE-1 (55 subjects) is used to evaluate results. Subjects with missing covariate assessment values are excluded from our analysis so the numbers of subjects in this paragraph are less than the numbers in individual study data described above.

The observed response rates of ACR20 at Week 12 are 59.3% in the upadacitinib 6 mg BID group, 34.5% in BALANCE-1 placebo group and 29.6% in SELECT-BEYOND placebo group. The relevant baseline covariates utilized for propensity score analyses for both clinical studies are presented in Table 2.

Table 2: Baseline demographics and disease characteristics from treatment group (Upadacitinib 6 mg BID from BALANCE-1 Study) and synthetic control group (Placebo Group from SELECT-BEYOND Study).

Propensity score methods

Propensity score is the conditional probability that a subject with given covariates will be assigned to a treatment group. Propensity score analysis methodology has been described in many previous literatures including but not limited to Williamson et al. [12], Rosenbaum and Rubin [13,19], Lunceford and Davidian [20], Austin and Mamdani [21], Xu and Ross et al. [22], Franklin and Eddings et al. [23] and references therein. In this paper, we determine propensity score using logistic regression with a set of baseline covariates and investigate those propensity score analysis methods using RCT data from rheumatoid arthritis studies described above. Specifically, four methods are investigated as summarized below.

Stratification: Stratification method is to stratify patients into groups (e.g., quintiles) by propensity score. Given that there are 54 subjects in the active treatment arm, we stratify the data into 5 strata, whereas each stratum has approximately 10 treated subjects. Overall treatment effect is evaluated by Cochran- Mantel-Haenszel (CMH) test stratified by the 5 propensity score strata.

Matching: Matching method is to match the upadacitinib 6 mg BID treated subjects from BALANCE-1 with the placebo subjects from SELECT-BEYOND and compare treatment effect in resulting matched pairs. The intention is to obtain matched 54 placebo subjects with one synthetic placebo subject matched with one upadacitinib treated subject. Based on optimal matching which minimizes a global measure of balance, 54 placebo subjects are identified to match the treatment group. As a comparison, we also perform greedy matching ("nearest neighbor matching") proposed by Rubin [24] with a caliper of 0.2 SD of logit of propensity score as recommended by Austin [14].

If multiple placebo subjects have propensity scores that are equally close to that of an upadacitinib treated subject exceeding the matching ratio, one of these placebo subjects will be selected at random. Subjects who are not selected in the matching process will be excluded from further analysis. Following matching, baseline covariates are summarized for upadacitinib treated subjects and matched historical placebo subjects to ensure balance being generally achieved.

Inverse Probability of Treatment Weighting (IPTW): As introduced in Rosenbaum’s original manuscript [25] and investigated in detail by Austin and Stuart [26], we have used an adjusted propensity score by weighting factors. Let Z_i be an indicator variable denoting whether the i-^th subject is treated. Let e_i denote the propensity score for the i-^th subject. The inverse probability of treatment weight can be defined as w_i=Z_i/e_i+(1-Z_i)/(1-e_i). This weight permits the estimation of average treatment effect, which takes a form of θ ̂=1/nΣ〖Y_i Z〗_i/e_i+1/nΣ(〖(1-Y_i)(1-Z〗_i))/(1-e_i), where Y_i is the outcome of i-th subject. We calculate a 95% Confidence Interval (CI) for treatment effect based on bootstrapping. 2000 bootstrap samples are generated from the data with replacement.

For each of the bootstrap sample, the weighted average estimate is calculated as θ ̂^*by replacing 〖(Y〗_i,Z_i) in θ ̂ with bootstrapped sample. 95% CIs are constructed by (〖θ ̂^*〗 _0.025,〖θ ̂^*〗_0.975), where 〖θ ̂^*〗_α denotes the 100 α % percentile of the bootstrapped estimate θ ̂^*. P-values are computed as the proportion of bootstrapped estimates with |θ ̂^*-θ ̂ |>|θ ̂|. Similarly, we also obtain a 95% CI for odds ratio based on bootstrap. For each of the bootstrap sample, the logodds of treatment effect is estimated by a logistic regression model regressing output Y on treatment Z with the prespecified weight. 95% CI for odds ratio is calculated by transforming the 2.5% and 97.5% percentiles of the bootstrap estimates of log-odds.

Covariate adjustment: We estimate the treatment effect of upadacitinib 6 mg BID vs. historical placebo data for ACR20 at Week 12 in a logistic regression model adjusting for propensity score. The odds ratio for upadacitinib 6 mg BID vs. synthetic control placebo group is estimated.

Austin [27] compared performance of stratification, matching and covariate adjustment for estimating marginal odds ratio and concluded that matching would result in estimators with the lowest Mean-Squared Error (MSE). Gayat et al. [28] compared stratification, matching and covariate adjustment in survival data analysis and demonstrated that stratified models showed poor performance while matching led to unbiased estimate of the treatment effect. Austin and Mamdani [21] illustrated the classic tradeoff between matching and stratification. Stratification may result in greater bias due to residual confounding within stratum. Matching may diminish the precision of the estimated treatment effect due to discarding several treated and untreated subjects. Gu and Rosenbaum [29] compared two matching procedures, optimal matching and greedy matching, and found that “optimal matching is sometimes noticeably better than greedy matching in the sense of producing closely matched pairs, sometimes only marginally better, but it is no better than greedy matching in the sense of producing balanced matched samples.” Franklin et al. [23]. compared the performance of propensity score methods with rare outcomes and testified that covariate adjustment and matching provide lower bias and MSE for rare binary outcomes. In this manuscript, we report results from all propensity score methods with the RCT data described in Randomized rheumatoid arthritis clinical trials. Specifically, we take one upadacitinib treated group from BALANCE-1 study, create a corresponding placebo group from SELECT-BEYOND study as the synthetic control arm, and perform the analysis using propensity-score-based methods as summarized above. The estimated treatment effects from propensity-score-based synthetic control arm are compared with those from the target randomized phase II study (i.e., the treatment effect between upadacitinib 6 mg BID and placebo groups from BALANCE-1 study). Notice that upadacitinib 6 mg BID in BALANCE-1 is the equivalent to upadacitinib 15 mg QD in study SELECTBEYOND which is the approved upadacitinib dose for rheumatoid arthritis indication.

Results

Propensity score is the probability of a subject being treated with upadacitinib 6 mg BID conditional on the subject’s baseline covariates. It is estimated using a logistic regression model including all the covariates in Table 2. Differences between the two groups are compared using chi-square test for categorical variables and two-sample t-test for continuous variables, respectively. Without any adjustment, we found that Rheumatoid Factor (RF), anti-Cyclic Citrullinated Peptide (anti- CCP) and duration of rheumatoid arthritis are significantly different among the two groups (p-value<0.05). Standardized Mean Difference (SMD) is also provided in Table 1 which compares the difference in means in units of the pooled standard deviation. The results are consistent with p-values (i.e., the smaller the p-values, the larger the SMD).

Table 2 indicates there exist unbalanced covariates such as that lower anti-CCP and prior bDMARDs received <3 are associated with a higher probability of being treated with upadacitinib 6 mg BID (p-value<0.1). The propensity score varies from 0.0194 to 0.7724. The distributions of propensity scores for two treatment groups are presented in Figure 1. The bars in Figure 1A shows the median and interquartile range. Figure 1B presents histogram of the propensity scores. As shown in Figures 1A and 1B, propensity scores are slightly higher in upadacitinib 6 mg BID treatment group in general. There is a good degree of overlap, i.e., 196 out of total 213 subjects with propensity scores between 0.060 and 0.651. Comparing with overall discrepancy, these plots show that propensity score discrepancy within most quintiles is smaller.

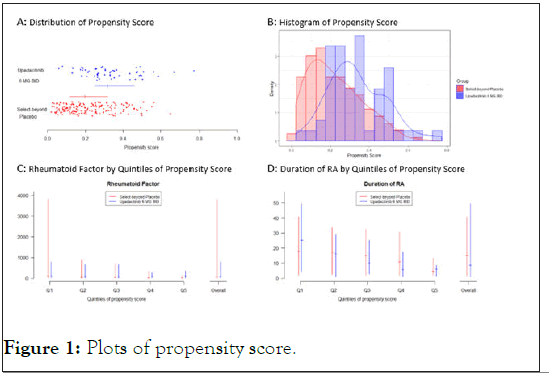
Figure 1: Plots of propensity score.

Table 3 shows the results from the propensity-score-based synthetic control arm as well as real BALANCE-1 results (benchmark) and non-propensity-score-based-results for upadacitinib 6 mg BID vs. SELECT-BEYOND placebo.

Table 3: Analysis results from treatment group (Upadacitinib 6 mg BID from BALANCE-1 Study) and synthetic control group (Placebo from SELECT-BEYOND Study).

Stratification: There are 85, 21, 21, 23 and 9 placebo subjects in the five strata (from lowest to highest quantiles) respectively with balanced strata for treatment group (Table 4). The estimated risk difference and odds ratio based on CMH method stratified by stratum are decreased from non-propensity-score-based analysis of 0.297 and 3.466 to 0.238 and 2.806 respectively, which is much closer to BALANCE-1 results of 0.247 and 2.756. 95% CIs and p-values are also much closer to BALANCE-1 results. Figures 1C and 1D show that discrepancy within most quintiles is smaller than overall discrepancy for RF and duration of rheumatoid arthritis. Similar results could also be seen in other covariates (not shown).

Table 4: Number of stratified subjects in each quintile.

Matching: The estimated risk difference and odds ratio based on the optimal matching (i.e., 1:1 matching or 54 matched pairs) are decreased from non-propensity-score-based analysis of 0.297 and 3.466 to 0.278 and 3.166 respectively. The greedy matching with a caliper of 0.2 SD of logit of propensity score further decreases them to 0.208 and 2.325 respectively. Both optimal and greedy matching results are improved from non-propensityscore- based analysis.

IPTW: The estimated risk difference and odds ratio based on IPTW by propensity score are decreased from non-propensity-score- based analysis of 0.297 and 3.466 to 0.187 and 2.389 respectively. The p-value for risk difference is 0.070 compared to BALANCE-1 p-value 0.008 and non-propensity-score-based analysis p-value<0.001. This indicates that the risk difference decreased too much in our example. For odds ratio, IPTW outcomes are closer to those from greedy matching.

Covariate adjustment: Logistic regression adjusting for propensity score shows the odds ratio decreases from non-propensity- score-based analysis of 3.466 to 2.879 which is close to BALANCE-1 result 2.756. Risk difference results are not available from logistic regression.

Comparing the p-values in Table 3, non-propensity-score-based analysis has the smallest p-value due to the largest treatment effects (i.e., the largest treatment difference and odds ratio) and large sample size. With the same sample size, stratification method has a small p-value following a little smaller treatment effect while IPTW has a much smaller treatment effect resulting in a non-significant p-value. Logistic regression adjusting for covariates or for propensity score led to similar results as the stratification method did. This indicates that, when sufficient covariates are included, logistic regression results for odds ratio from non-propensity-score-based analysis is very similar to those from propensity-score-based methods. With a smaller sample size excluding unmatched subjects, optimal matching maintained a similar p-value as stratification method due to the large treatment effect within the matched subjects. However, results of greedy matching showed a smaller treatment effect resulting in a bigger p-value. Comparing with BALANCE-1 p-value, optimal matching gives better results (closer to BALANCE-1 results) than greedy matching procedure. Overall, the results from stratification are the closest results to the real randomized BALANCE-1 results. This indicates that five strata are appropriate for our data. As explained by Williamson et al. [12], a small number of strata will cause bias due to residual confounding within strata. This bias could be greatly reduced by creating more strata. Ideally, each stratum should contain a single propensity score. In practice, one could divide the sample at percentiles of propensity score to create equal-sized groups. Results from optimal matching for risk difference and covariate adjustment for odds ratio are also comparable to the real BALANCE-1 results. A similar p-value in stratification and optimal matching demonstrates that the stratification method with enough strata is closer to the optimal matching procedure.

The same procedures are repeatedly performed for randomized studies BALANCE-1 upadacitinib 6 mg BID (N=54) vs. concurrent placebo (N=55) and SELECT-BEYOND upadacitinib 15 mg QD (N=155) vs. placebo (N=159) respectively. The results are presented in Table 5 and Table 6. Comparing with non-propensity score analysis results (i.e., real RCT results in the first row), the findings are as follows. For BALANCE-1 study data analysis, Table 5 shows that stratification and optimal matching work well; greedy matching is bad due to reduced sample size; IPTW is not good despite large treatment difference; and logistic regression adjusted for propensity score is in between. For SELECT-BEYOND study data analysis presented in Table 6, all results are very close due to the randomized data and the large sample size.

Table 5: Analysis results from BALANCE-1 study (Upadacitinib 6 mg BID vs. Placebo).

Table 6: Analysis results from SELECT-BEYOND study (Upadacitinib 15 QD mg vs. Placebo).

Discussion

A clinical trial without a placebo control group would greatly encourage patients to join in the study. In this scenario, constructing a synthetic control group is an ideal approach to analyze treatment effect for the trial. We have described how we created a synthetic control arm for the target RA study using propensity-score-based methods, and compared the estimated treatment effects between the in-trial active arm and the synthetic control arm with the benchmark. Our results demonstrate that the synthetic control arm created with the propensity-score-based stratification and matching methods could provide an estimate of treatment effect that is as accurate as that of a real randomized clinical trial. This suggests a good opportunity to expedite drug development with reduced cost.

While randomized clinical trials are very powerful and stand as an almost sacred principle, synthetic control could serve as a supplement to randomized clinical trials. For clinical studies without a control group, propensity-score-based synthetic control arm can be used to provide treatment effect estimates with improved accuracy by taking relevant baseline covariates into consideration. We demonstrate that, among all the propensity-score-based methods, stratification method (with CMH method stratified by stratum for binary endpoints) and optimal matching provided better results as the real randomized trial when sample size is moderate as in BALANCE-1 study (i.e., around 50). For large sample sizes as in study SELECT-BEYOND, all methods perform well.

Our general findings are consistent with Austin and Mamdani [21]. Within the matching method, optimal matching procedure shows better results than greedy procedure which is consistent with Gu and Rosenbaum [29]. Matching and stratification should perform very similarly if enough number of strata is considered for stratification.

One issue we have not mentioned is whether the matching should be performed “with replacement”. Since we have enough external control subjects, we thought it is not necessary to perform matching with replacement. In the case where there are a few patient-level control data compared with the data in the treatment group one wants to match, matching with replacement can be a useful choice as recommended by Dehejia and Wahba [30]. An obvious drawback from matching with replacement is that less unique control individuals would be selected as matches comparing with matching without replacement. Therefore, we do not recommend matching with replacement. Instead, Bayesian historical data borrowing methods are recommended for the case with fewer individual control data.

Consideration must also be made for choosing appropriate baseline covariates for propensity score calculation. In this manuscript, we consider using those baseline variables that are potentially influential on the clinical outcomes from rheumatoid arthritis clinical experts. Since only those covariates commonly available in both current and historical studies are able to be included in the logistic regression model, historical study data should be carefully selected with sufficient baseline information to determine the propensity score in addition to comparability between historical and current data.

While Bayesian approach has been widely discussed and applied in clinical trials incorporating historical control data, this article is intended to introduce the propensity-score-based synthetic control analysis methods as an alternative approach in reducing bias between treatment and synthetic control groups. Propensity-score- based stratification and matching methods could provide an accurate estimate of treatment effect as a real randomized clinical trial. We encourage extended use of these methods in clinical research for the new drug development. When historical control data is limited or there are no patient-level data, Bayesian historical data borrowing could be considered with group-level data as the prior information, which will be updated as posterior belief when current control data (with reduced sample size in design) become available. If there are sufficient patient-level historical control data, the propensity-score-based synthetic control arm described in the manuscript is advocated.

References

1. Thorlund K, Dron L, Park JH, Mills EJ. Synthetic and external controls in clinical trials
2. Lin JJ, Gamalo-Siebers M, Tiwari R. Propensity score matched augmented controls in randomized clinical trials: A case study. Pharm Stat. 2018;17:629-647.
3. Chiodo GT, Tolle SW, Bevan L. Placebo-controlled trials: Good science or medical neglect? West J Med. 2000;172(4):271
4. Pocock SJ. The combination of randomized and historical controls in clinical trials. J Chron Dis. 1976;29:175-188.
5. Neuenschwander B, Capkun-Niggli. Summarizing historical information on controls in clinical trials. Clin Trials. 2010;7:5-18.
6. Schmidli H, Gsteiger S. Robust meta-analytic-predictive priors in clinical trials with historical control information. Biometrics. 2014;70:1023-1032.
7. Ibrahim JG, Chen MH. Power prior distributions for regression models. Stat Sci. 2000;15:46-60.
8. Duan Y, Ye K, Smith EP. Evaluating water quality using power priors to incorporate historical information. Environmetrics. 2006;17:95-106.
9. Neuenschwander B, Branson M, Spiegelhalter DJ. A note on the power prior. Stat Med. 2009;28:3562-3566.
10. Hobbs BP, Sargent DJ, Carlin BP. Commensurate priors for incorporating historical information in clinical trials using general and generalized linear models. Bayesian Analy. 2011;7:639-674.
11. Murray TA, Hobbs BP. Semiparametric bayesian commensurate survival model for post-market medical device surveillance with non-exchangeable historical data. Biometrics. 2014;70:185-191.
12. Williamson E, Morley R, Lucas A Carpenter J. Propensity scores: From naive enthusiasm to intuitive understanding. Stat Methods Med Res. 2012;21(3):273-293.
13. Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70:41
14. Austin PC. An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivariate Behav Res. 2011;46:399-424.
15. Davi R, Ferris A. Exploring Whether a Synthetic Control Arm can be derived from Historical Clinical Trials that Match Baseline Characteristics and Overall Survival Outcome of a Randomized Control Arm: Case Study in Non-Small Cell Lung Cancer. Friends of Cancer Research. 2020.
16. Schwartz M, Ries A. Rectus femoris transfer in children with cerebral palsy: Comparing a propensity score-matched observational study to a randomized control trial. Dev Med Child Neurol. 2021;63(2):196-203.
17. Kremer JM, Emery P. A phase IIb study of ABT-494, a selective JAK-1 inhibitor, in patients with rheumatoid arthritis and an inadequate response to anti-tumor necrosis factor therapy. Arthritis Rheumatol. 2016;68(12):2867-2877.
18. Genovese MC, Fleischmann R. Safety and efficacy of upadacitinib in patients with active rheumatoid arthritis refractory to biologic disease-modifying anti-rheumatic drugs (SELECT-BEYOND): A double-blind, randomised controlled phase 3 trial. Lancet. 2018;391(10139):2513-2524.
19. Rosenbaum PR, Rubin DB. Constructing a control group using multivariate matched sampling methods that incorporate the propensity score. J Ame Stat Ass. 1985;39:33
20. Lunceford JK, Davidian M. Stratification and weighting via. the propensity score in estimation of causal treatment effects: A comparative study. Stat Med. 2004;23:2937
21. Austin PC, Mamdani MM. A comparison of propensity score methods: A case-study estimating the effectiveness of post-AMI statin use. Stat Med. 2006;25:2084
22. Xu S, Ross C. Use of stabilized inverse propensity scores as weights to directly estimate relative risk and its confidence intervals. Value Health. 2010;13:273-277.
23. Franklin JM, Eddings W. Comparing the performance of propensity score methods in healthcare database studies with rare outcomes. Stat Med. 2017;36:1946-1963.
24. Rubin DB. Matching to remove bias in observational studies. Biometrics. 1973;29:159-184.
25. Rosenbaum PR. Model-based direct adjustment. J Ame Stat Ass. 1987;82(398):387-394.
26. Austin PC, Stuart EA. Moving towards best practice when using Inverse Probability of Treatment Weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies. Stat Med. 2015;34:3661-1679.
27. Austin PC. The performance of different propensity score methods for estimating marginal odds ratios. Stat Med. 2007;26:3078-3094.
28. Gayat E, Resche-Rigon M, Mary JY, Porcher R. Propensity score applied to survival data analysis through proportional hazards models: A monte carlo study. Pharm Stat. 2012;11:222-229.
29. Gu X, Rosenbaum PR. Comparison of multivariate matching methods: Structures, distances, and algorithms. J Comput and Graph Stat. 1993;2:405
30. Dehejia RH, Wahba S. Propensity score matching methods for non-experimental causal studies. Review of Econ Stat. 2020;84:151