Significant effects of intraparticle mass transfer on separation result in single chromatographic column have been realized by many researchers [1-10]. But the effects of intraparticle mass transfer on simulated moving bed (SMB) process have seldom been reported. In practice, the flow rate varies in different zones of SMB and sometimes is high when the SMB is run, and then the influence of intraparticle mass transfer is important and becomes significant.

It is the goal pursued by every user of SMB that choose the appropriate operating conditions for SMB and then obtain the optimal separation result. And practically, the complete separation region in m₂-m₃ plane is generally the key for the determination of the operating conditions of SMB, where m₂ and m₃ are the ratios of net fluid flow rate to net solid flow rate in second and third zone of SMB, respectively. Under ideal conditions, the complete separation region of SMB can be easily obtained according to the results in literatures [11-13]. While for the situations that the mass transfer resistances exist, such separation region has to be calculated based on the numerical solution of the model of SMB.

The General Rate (GR) model which involves the effect of intraparticle mass transfer processes is used as the model for single column of SMB in this work. And a modified equilibrium dispersive (MED) model of which the numerical solution is equivalent to that of GR model is used in this work to simplify the calculations. The influence of different levels of intraparticle mass transfer parameters, i.e., effective diffusivity and external mass transfer coefficient on separation region (purities above 99%) for binary mixture in four-zone SMB is investigated and then explained by the results in the C₁-C₂ space of binary mixture separation under same conditions in single column.

For single column of SMB units, the General Rate (GR) model [1], which involves the effects of intraparticle mass transfer processes but neglects the process of adsorption/desorption, is adopted in this work, because in most cases the kinetic process of adsorption/desorption is fast enough and its contribution to the overall mass transfer processes can be neglected [1]. The model parameters are considered to be same for two components for the sake of simplification. And then the model equations can be written as follows,

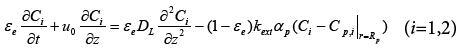(1)

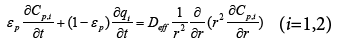(2)

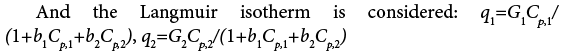
The initial conditions are: C_i (0, z)=0, q_i (0, z)=0, C_p,i (0, z, r)=0 (0p)

The boundary conditions are

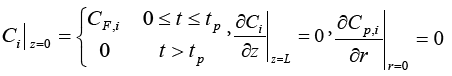
And the joint condition of the two mass balance equations above at

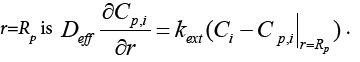
In equations above, C_i and q_i are concentrations of component i in mobile and stationary phase, respectively. C_p,i is the concentration of component i in intraparticle stagnant mobile phase, D_L the axial dispersion coefficient, 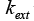the external mass transfer coefficient, 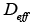the effective diffusivity, 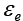the external porosity, 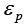the internal porosity, u₀ the superficial velocity of mobile phase, the average radius of the packing particles, 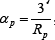,L the length of the column, t_p the injection time, C_F,i the feed concentration, t the time, G_i and b_i are Langmuir isotherm parameters, r and x are the space coordinates along column axis and pore radius, respectively.

The calculation of separation region of SMB using GR model directly as the single column model for SMB units is not easy. In fact, it is computation intensive and extremely time-consuming. And then a simplified but equivalent method for solving the problem is expected.

A modified equilibrium dispersive (MED) model has been developed [14] and can replace the GR model to simplify the numerical calculations. Therefore, the total band broadening originated from axial dispersion and intraparticle mass transfer processes can be considered equal to the band broadening resulted from an equivalent axial dispersion, which represented by axial dispersion coefficient D_eq,i in the modified equilibrium dispersive (MED) model. The modified equilibrium dispersive (MED) model is as follows,

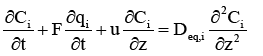(12)

Where 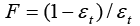is the phase ratio (total column porosity 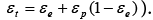And the initial and boundary conditions for C_i and q_i are same with that of GR model above.

The HETP equation for the GR model is deduced from the moment equations of the model [15], and it is written as below,

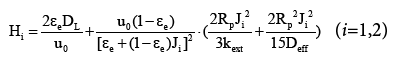(4)

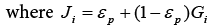
And then the equivalent axial dispersion coefficient 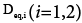can be obtained.

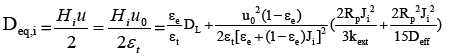(5)

A four-zone SMB which involves two columns per zone is considered in this work. And the values of some parameters needed for calculations are listed as follows. Column length L=12 cm, column diameter R=1 cm, external porosity 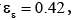internal porosity , R_p=15 micron, feed concentration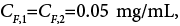 Langmuir isotherm parameters 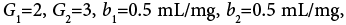axial dispersion coefficient DL=0.01 cm²/min. The operating parameters for the first and fourth zone of SMB are considered as far away from their critical values, and the switch time of SMB is 2 min, the flow rates in the first and fourth zones are 33.9 mL/min and 18.8 mL/min, respectively.

To obtain the edge of separation region of SMB, the lattice with 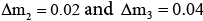is drawn in m₂-m₃ plane. The average cyclic steady-state purities of the products from extract and raffinate ports of SMB are calculated under the operating conditions corresponding to the lattice points in m₂-m₃ plane. And the separation region of SMB in m₂-m₃ plane is formed by the lattice points where both purities of less retained component from raffinate port and more retained component from extract port are higher than 99%. The calculations above are carried out for different levels of intraparticle mass transfer parameters to show the effect of these parameters.

The modified equilibrium dispersive (MED) model above is employed to obtain the numerical solutions equivalent to that of the GR model. Firstly, Equation (3) is discretized with the method of orthogonal collocation on finite elements. And then, the discretized ordinary differential equations were solved by Runge-Kutta method of order four.

The separation region of SMB is calculated at different levels of intraparticle mass transfer parameters, i.e., effective diffusivity D_eff and external mass transfer coefficient k_ext. The ranges of values of these parameters were determined according to the literatures [2,4-6].

The separation regions of SMB calculated at four levels of D_eff are shown in Figure 1. The triangles in the figure are corresponding to the separation regions under different conditions, and are named as Triangle 1, Triangle 2, Triangle 3 and Triangle 4, respectively and in the order of decrease of D_eff. It is clear that the triangle shrinks remarkably when D_eff decreases from 1 × 10^-4 cm²/min to 5 × 10^-6 cm²/min. And more specifically, with decrease of D_eff , the upper side of the triangle moves downwards remarkably and almost vertically. The upper sides of the triangles obtained under higher D_eff turn gradually upward slightly with increase of m3, but for the triangles obtained under lower D_eff , this gradual raise can not be observed. While for the left side of triangle, it moves rightward when D_eff decreases. But the points in left side of triangle move rightward in different distances. The points near the diagonal move farther than those far from it. In summary, the decrease of D_eff affects the two sides of the separation region in different ways; the upper side moves downwards farther with its slope decreases slightly; while for the left side, its slope decreases remarkably and at the same time it moves rightward but not so far as the upper side does.

Figure 1: Separation regions (purities above 99%) of four-zone SMB calculated under different levels of effective diffusivity and with external mass transfer coefficient equal to 1 cm/min.

The external mass transfer coefficient has similar effect on the separation region of SMB. The result is shown as Figure 2. With the value of k_ext decreases from 10 cm/min to 0.1 cm/min, the corresponding calculated separation region of SMB shrinks slightly. The upper side of the triangle moves downwards and the left side of the triangle moves rightward. And it seems that the reduction of the area of the separation region is mainly due to downward movement of the upper side of the separation region rather than the rightward movement of the left one. And compared with the triangles in Figure 1, the difference between the triangles in Figure 2 is much less.

Figure 2: Separation regions (purities above 99%) of four-zone SMB calculated under different levels of external mass transfer coefficient and with effective diffusivity equal to 5 × 10^-5 cm²/min.

The results shown in Figures 1 and 2 indicate that slowing the intraparticle mass transfer processes would reduce the separation region of SMB. And the change of the separation region is more sensitive to the decrease of effective diffusivity than that of external mass transfer coefficient in their ranges which generally reported in literatures.

In fact, the results of the effect of intraparticle mass transfer parameters on the separation region of SMB mentioned above is easy to understand when the result of the binary mixture separation in single column in C₁-C₂ space is considered. The sample feeding style is a wide rectangle injection of binary mixture solution which is similar with that of SMB. The effects of effective diffusivity on the separation results in C₁-C₂ space of a wide rectangular pulse of binary mixture solution eluted in single column are presented here for the explanation of the point.

Figure 3 shows the results of different levels of intraparticle effective diffusivity when the binary mixture solutions of lower and higher concentrations are fed, respectively. The following points can be concluded according to Figure 3. At first, different from two straight lines in C₁-C₂ space under ideal condition [16], the lines in C₁-C₂ space curve and are tangent with the coordinate axes when they approach the axes. And with the decrease of effective diffusivity, the tangent points get closer to the coordinate origin. The shorter distances between the tangent points and the coordinate origin mean the lower concentrations of two pure components taken from the binary mixture. That is to say, with the decrease of effective diffusivity, the complete separation of binary mixture in single column gets more difficult. Secondly, the influences of the nonlinearity which caused by the increase of feed concentration on the fronts and the rears of eluted band profiles are different. When lower concentration of binary mixture being fed, with the decrease of effective diffusivity, the straight part of the line in C₁- C₂ space corresponding to the fronts of eluted band profile shortens and disappears eventually. While with the higher sample concentration being fed, all these lines are curved. The difference between the lines under different levels of D_eff is always obvious whether for the situation of lower or higher concentration of binary mixture being fed. In other words, the increase of the feed concentration can only slightly reduce the difference between the fronts of the eluted band profiles calculated under different levels of effective diffusivity. That is to say, the influence of effective diffusivity is stronger than that of concentration nonlinearity on the lines in C₁-C₂ space corresponding to the fronts of eluted band profiles. But the situation for the lines in C₁-C₂ space which corresponding to the rears of eluted band profiles is much different. When the feed concentration increases, the difference between these lines almost disappears completely. And this indicates that the increased concentration nonlinearity strongly diminishes the difference between the rears of eluted band profiles calculated at different levels of effective diffusivity.

Figure 3: Numerical results in C₁-C₂ space of a wide rectangular injection of binary mixture solution eluted in single column which calculated under different levels of effective diffusivity and with external mass transfer coefficient equal to 1 cm/min (a) feed concentrations are 0.05 mg/mL; (b) feed concentrations are 8 mg/mL.

Now, the effects of effective diffusivity on the separation region of SMB can be interpreted based on the understanding of the results in C₁-C₂ space for binary mixture separation in single column.

Firstly, Figure 3a and 3b shows that with decrease of effective diffusivity, the complete separation of binary mixture in single column gets more difficult. And this can be the explanation for the result shown in Figure 1 that the separation region reduces when effective diffusivity decrease.

Secondly, as we know, the left side of the triangle (separation region) for SMB indicates the left border of the region in m₂-m₃ plane beyond which the pure more retained component (C₂) can not be obtained from extract port of SMB. So, the behavior of the lines in C₁- C₂ space corresponding to the rears of eluted band profiles in single column under different levels of effective diffusivity can be employed here to understand the effect of effective diffusivity on the left boundary of separation region of SMB. On the other hand, the upper side of the triangle in m₂-m₃ plane is the border of the separation region for SMB beyond which the pure less retained component (C₁) can not be collected from raffinate port of SMB. And the results discussed above about the lines in C₁-C₂ space corresponding to the fronts of eluted band profiles under different levels of effective diffusivity should be used to explain the effect of effective diffusivity on the upper side of separation region.

To facilitate the explanation, two solid straight lines are drawn in Figures 1 and 2, which named as L₁ and L₂, respectively. They are arbitrary lines parallel with the diagonal of m₂-m₃ plane, but L₂ is near the diagonal and L₁ far from it. When the SMB is operated along each one of the two lines, m₂ and m₃ increase synchronously and the feeding flow rate keeps constant. Line L₁ is corresponding to the higher feeding flow rate compared with line L₂. The higher feeding flow rate means more quantity of binary mixture being fed into the columns in the third zone of SMB per minute. Although the same concentration is fed, compared with the lower feeding flow rate along line L2, the operating condition of higher feeding flow rate along line L1 means the stronger nonlinear effect in the columns of SMB which similar with that aroused by high concentration in single column. Therefore, it is easy to understand that in Figure 1, the distances between the left sides of the triangles along line L₁ is much less than that along line L₂. For it has been stated in the discussion about Figure 3 that the increased nonlinearity strongly diminishes the difference between the rears of band profiles eluted from single column under different levels of effect diffusivity. As for the upper sides of the triangles in Figure 1, the remarkable difference between them along line L₁ is nearly same with that along line L₂ except for the slightly upward deviation of the points which obtained under the condition of Defi=1 × 10^-4 cm²/min. The reason for the phenomenon is as follows. Just as what mentioned above according to Figure 3, the influence of effective diffusivity is much stronger than that of concentration nonlinearity on the lines in C₁-C₂ space corresponding to the fronts of eluted band profiles. Therefore, the increase of feed concentration only slightly reduces the difference between the fronts of the eluted band profiles calculated under different levels of effective diffusivity.

A similar interpretation as above can be applied for the effect of external mass transfer coefficient (kext) on the separation region of SMB shown in Figure 2.

The stronger influence of concentration nonlinearity on the left sides of separation regions of SMB under different levels of effective diffusivity is an important result for practice. Because in most cases, we hope the objective component of separation is collected in the extract port of SMB. The result above indicates that the purification process of more retained component (C₂) is sensitive to either nonideal or nonlinear factors. Therefore, careful determination of the operation condition of SMB is necessary and this is especially important for the separation involves slow intraparticle mass transfer process.

In summary, the main conclusions as follows are obtained. Firstly, the influence of effective diffusivity is more than that of external mass transfer coefficient on the SMB process in practical range of these parameters. Secondly, the separation region of SMB shrinks in the following style with the decrease of intraparticle mass transfer parameters (D_eff and k_ext). The upper side of separation region moves downwards evidently and with its slope decreasing slightly; the left side of separation region moves rightward but with its slope decreasing obviously. The behaviors of the separation region of SMB above can be explained by the result in C₁-C₂ space of binary mixture separation in single column.