Journal of Chromatography & Separation Techniques
Open Access
ISSN: 2157-7064
ISSN: 2157-7064
Research Article - (2017) Volume 8, Issue 5
In order to obtain the most valuable information the Gibbs free energies of adsorption or solution, ΔG, should have been estimated in three ways on the basis of the retention times of the centre of gravity of the elution peak of the substances with defined physico-chemical properties. The temperature dependent van der Waals component of the surface free energy, dW s ν γ , has been estimated by employing the Dorris-Gray method and the Schultz method. The suggested approach has also been employed for carbon adsorbents on the basis of various literature data.
Keywords: Liquid crystalline stationary phases; Surface free energy of adsorption; Inverse gas chromatography
Inverse gas chromatography (IGC) is usually employed as a dynamic technique of measure how the retention time (both of the maximum peak and the centre of gravity) changes as a function of:
i. Probe molecule of known acceptor-donor properties which peculiarly interacts with the outermost layer of the liquid crystal (LC) atoms and more weakly with the molecules (atoms) in bulk,
ii. Probe molecule size which must be regarded therefore molecular sieving by stationary phase is caused by the size and/or shape differences between the LCSP aperture dimensions and the probe molecule,
iii. Probe molecule concentration is important therefore at infinite dilution probe-probe interactions can be assumed negligible and any retention is only due to probe- stationary phase interactions,
iv. Correct and stable value of carrier gas flow rate.
The data set obtained enables to elucidate a wide range of physicochemical properties of solid and liquids (as stationary phases) under investigation. Different LCs, being usually elongated molecules with different numbers of polar and nonpolar functional groups are deposited on neutral solid support and placed in chromatographic columns to determine a plausible quantitative description of the acceptor-donor interactions of these probes with the randomly ordered LCs molecules. As is commonly known an acceptor is an atom, functional group or ion, to which electrons are donated in the formation of a coordinate bond, while a donor is a group, atom or ion that provides a pair of electrons in forming similar kind of bond [1]. It is necessary to emphasise that according to Jensen the Lewis acid-base interactions encompass [2]:
1. The electron pair acceptor-donor interactions.
2. The electrophile-nucleophile interactions.
The aforesaid interactions determine the nature and energy of the LCs interactions with probes and therefore they can be profitably controlled by the adsorption and absorption (dissolution) of the testing substance. Interaction with a surface of LC solid state and the state of adsorbed molecules of probes on such a surface allow more readily of theoretical treatment than do the apparently independent interactions (dispersion, electrostatic, repulsive, and chemical) with a solution in a liquid film of the LCs. Thus, all the molecules in a solution are mobile and so interact with fluctuating parts, whereas the molecules adsorbed on a reasonably smooth solid surface of the LCs interact mainly with the nearest force centres, which are fixed.
It is known that various interactions between liquid crystal molecule and testing molecule range from essentially molecular (nonspecific and specific), with the chemical individuality of the partners retained, to chemical, with the individuality lost and a new surface compound formed.
The liquid crystalline stationary phases were introduced into chromatographic practice at the beginning of sixties last century [3]. Since that time, they have been still employing in the most correct analysis of diverse analytes mixtures in both gas and liquid chromatography. On the ground of the increasing requirements on analytes of isomeric compounds and the problems encountered in their separation demand a study of more diverse analytical systems which are characterized by a higher selectivity is still on time. Therefore, apart the selectivity and polarities of various liquid crystals (i.e., rodlike, banana-shape, biforked, oxygen, sulphur, nitrogen and metal containing molecules, Schiff-base, and polymeric dendrimers) their surface free energy properties have to be very precisely elucidated.
A significant amount of the physicochemical measurements can be successfully performed by inverse gas chromatography (IGC). It is a dynamic technique in which the defined chromatographic support with deposited the tested liquid crystal (or liquid crystals mixture) is under investigation while a probe (testing substance) in the mobile phase is employed as probes of known properties.
The total free energy of transferring a mole of substance vapour from the gas phase to a standard state on the liquid crystalline phase surface can be estimated in a threefold way as dependencies based on the specific retention volume referred to the centre of gravity of the elution peak and to 1 g of liquid crystal (LC) in a column,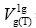 [4]:
[4]:
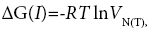 (1)
(1)
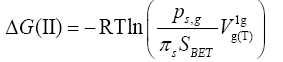 (2)
(2)
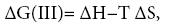 (3)
(3)
where: Ps– is a reference pressure having a value of 1 atm (101325 N/m2);
πs – is the two-dimensional pressure of the adsorbed state, 0.338.10-3 N/m [5];
VN(T) – is the net retention volume of the tested liquid crystal in chromatographic column;
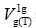 -is the specific retention volume referred to one gram of the tested liquid crystal in chromatographic column,
-is the specific retention volume referred to one gram of the tested liquid crystal in chromatographic column,
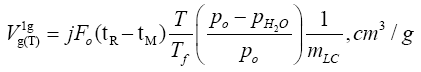
ΔH and ΔS – are the differential enthalpy and entropy of solution and adsorption [6], respectively, calculated from the following dependency:
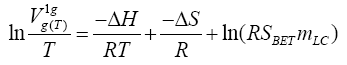
j - is the James-Martin compressibility factor;
Fo -is volumetric flow rate of the carrier gas through the column, measured by soap flow-meter at the constant column temperature, T;
Tf - is the temperature of the flow-meter;
tR - is the retention time of the probe;
tM - is the hold-up time;
po - is pressure at the column outlet;
pH2O - is the pressure of water vapour at environment temperature;
mLC - is the mass of liquid crystal in the column. It is conspicuously seen that for a given chromatographic system, i.e., the Ps,g , πs and SBET values are constant, the equation (2) changes to
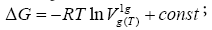
mLC - is the mass of liquid crystal in column, and SBET its specific surface area [4,7].
The 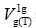 values illustrate an affinity of the LCSPs tested for the testing substances used. From the thermodynamic point of view the aforesaid affinity indicates a standard variation in the free energy of adsorption, ΔGads, and dissolution,
values illustrate an affinity of the LCSPs tested for the testing substances used. From the thermodynamic point of view the aforesaid affinity indicates a standard variation in the free energy of adsorption, ΔGads, and dissolution, 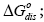 for a given standard state it is just the measure of the specific interactions.
for a given standard state it is just the measure of the specific interactions.
In this context, it is necessary to emphasise that the molar differential energy, ΔG, must be regarded as:
i. Molar differential Gibbs free energy of adsorption of the testing substances molecules on the surface of the crystalline form of the LCSP tested,
ii. and molar differential Gibbs free energy of solution of the testing substances molecules being discrete and mixed with the molecules of LCs in their nematic and smectic phases.
Making numerous attempts of the application of new liquid crystalline stationary phases (LCSPs) having a diversity of functional groups, which possess different surface energetical properties, a growth of interest in tests of the systems properties: LCSP-the chromatographed probe, seems to be intelligible [3]. The interactions of testing substance molecules, mainly between the outermost atoms of the tested LCs species, and a number of atoms in bulk can be divided into two principally different kinds, namely [2,8]:
1. The van der Waals interactions have an electro-dynamic origin as they arise from the attracting or repelling forces between LCs molecules (or between parts, having different atoms, of the same molecule) other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral molecules.
The term is also sometimes used loosely as a synonym for the totality of intermolecular forces, and it includes:
a. the London (or dispersion) force which is the dispersion interaction between two induced dipoles (or fluctuating dipoleinduced dipole);
b. the Debye force which is the induction interaction between one induced dipole and one permanent dipole (induced dipolepermanent dipole);
c. the Keesom force which is the orientation interaction between two permanent dipoles (permanent dipole-permanent dipole);
In this context, it is necessary to realise that the Debye and Keesom interactions are found only among molecules which have permanent dipole moments.
2. The Pearson acceptor-donor interactions, including hydrogen bonds being a significant subset of them. However, it is necessary to realise that in chemistry there are six, quite distinct types of Lewis acid and four quite distinct types of Lewis base taken into account, where the distinction is described by frontier molecular orbital topology. It follows that the six types of Lewis acid and the four types of Lewis base inevitably interact to give 24 distinct types of Lewis acid-base complexes [8].
The surface free energy, γs , describes the physical interaction potentials of the probes and liquid crystalline layers. Whence, it has the nature of the forces across interfaces, viz., interfacial energy, intermolecular forces or intermolecular potential [9]. According to the fundamental Fowkes’ formalism the surface free energy of any substance can be written as a sum of dispersive (non-specific) and nondispersive (specific) contributions [10]:
• a dispersive component (introduced by Fowkes) is denoted as  and pertaining to London attraction,
and pertaining to London attraction, ;
;
• a specific component, denoted as 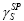 or
or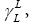 which describes all other types of interactions (Debye, Keesom, hydrogen bonding, and other polar effects).
which describes all other types of interactions (Debye, Keesom, hydrogen bonding, and other polar effects).
Thus the total surface free energy is given by:
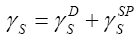
The term γDS , introduced by Fowkes [11] has been interpreted in a number of papers as the dispersive component of the surface free energy. However, van Oss et al. [12] and Goss [13] have shown that this magnitude includes all three types of van der Waals interactions.
Dorris and Gray have assumed that the free energy of adsorption of a methylene group, −ΔGCH2 , can be correlated to its work of adhesion, WCH2 ,with the LC surface, in the following way [14]:
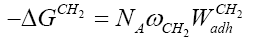 (4)
(4)
Inverse gas chromatography at infinite dilution conditions has been employed just to determine the nature of both, liquid crystalline form and liquid crystalline phases. In a well defined adsorptive chromatographic process, the incremental adsorption free energy of a methylene group in an n-alkane molecule, −ΔGCH2 , can be calculated from the slope of the natural logarithm of the net retention volume of the reference substances, i.e., consecutive n-alkanes, and it can be expressed as:
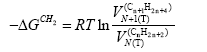 (5)
(5)
where: 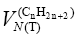 and
and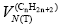 are the net retention volumes of consecutive n-alkanes having n+1 and n methylene groups in their molecules, respectively.
are the net retention volumes of consecutive n-alkanes having n+1 and n methylene groups in their molecules, respectively.
In the well characterised adsorption and solution system, where methylene groups interact with the outermost layer of species of an organic molecule [15]:
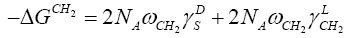 (6)
(6)
where 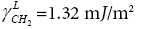
Regarding the fact, that Zettlemoyer has employed an arithmetical mean, into the Equation (6) as did [16], is not meaningful for the application of the geometric or harmonic means, because both have given the important differences in the two considered parameters, 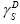 and
and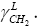
While Park and Brendle have simplified the equation (6) in the case if the contribution of the dependency 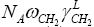 has been less than 2 % of the tested material, then the equation (6) can be expressed in the following form [15]:
has been less than 2 % of the tested material, then the equation (6) can be expressed in the following form [15]:
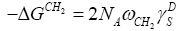 (7)
(7)
In the simplified equation (7) all the terms are either known [ NA , ωCH2 ] or measurable −ΔGCH2 excluding the quantity of interest γDS .
As was described earlier, the ΔG ads values are useful, because they allow us to obtain the dispersive component,
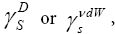 employing the procedure presented earlier. Dorris and Grey employed the semi-empirical relationship to determine the
employing the procedure presented earlier. Dorris and Grey employed the semi-empirical relationship to determine the 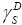 component of the surface free energy [14]. This relationship is based on the incremental change in ΔG ads per methylene group for a series of n-alkanes. The value of the dispersive component of the surface free energy can be calculated by employing the following dependencies:
component of the surface free energy [14]. This relationship is based on the incremental change in ΔG ads per methylene group for a series of n-alkanes. The value of the dispersive component of the surface free energy can be calculated by employing the following dependencies:
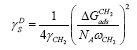 [19] or
[19] or 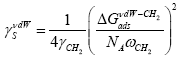 (8b)
(8b)
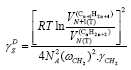 [20,21] (vide Eqs 4 and 5), (8c)
[20,21] (vide Eqs 4 and 5), (8c)
where π0 is the spreading pressure at the saturated vapour pressure of liquid testing substances;
γL is the surface free energy of the pure liquid phase [17];
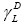 is the dispersive component of the surface free energy of the liquid or testing substance injected;
is the dispersive component of the surface free energy of the liquid or testing substance injected;
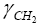 is the surface energy of polyethylene-type polymers with a finite molecular weight, given after Aveyard by [22]:
is the surface energy of polyethylene-type polymers with a finite molecular weight, given after Aveyard by [22]:
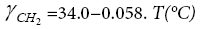 (9a)
(9a)
and by Mukhopadhyay and Schreiber [23], and by Voelkel [24]:
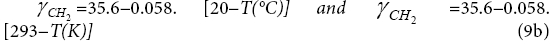
and by Milonji? [25]:
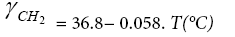 (9c)
(9c)
where: 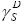 is expressed in mJ/m2.
is expressed in mJ/m2.
The 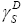 and
and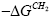 values depend on the differential quantities −ΔGCH2 and ΔGν dW−CH2 , respectively. They are independent of the surface area of the tested material and for that reason they are fundamental parameters which give information concerning the surface free energy of the solid state. It is necessary to realise, that the equations (9b) and (9c) have not been employed in the comparison tests of the van der Waals component of the surface free energy,
values depend on the differential quantities −ΔGCH2 and ΔGν dW−CH2 , respectively. They are independent of the surface area of the tested material and for that reason they are fundamental parameters which give information concerning the surface free energy of the solid state. It is necessary to realise, that the equations (9b) and (9c) have not been employed in the comparison tests of the van der Waals component of the surface free energy, 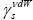 , of LCSPs up until now. This is our novel approach for the aforesaid liquid crystalline materials.
, of LCSPs up until now. This is our novel approach for the aforesaid liquid crystalline materials.
The other method of the determination of the 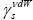 values has been evaluated by Schultz et al. [21]. Its background has been connected with the relation between the molar free energy of adsorption, ΔG, and the net retention volume, V N( T ) :
values has been evaluated by Schultz et al. [21]. Its background has been connected with the relation between the molar free energy of adsorption, ΔG, and the net retention volume, V N( T ) :
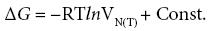 (10)
(10)
Taking the earlier Hüttinger et al. [26] approache into account and more contemporary suggestions made by van Oss [12,27] and Goss [13], we can state:
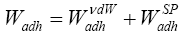 (11a)
(11a)
and with regard to the Girifalco and Good [28], and Fowkes suggestions we obtain:
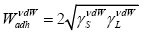 (11b)
(11b)
For non-polar compounds, it could be safe to assume that interactions at the outermost layer of stationary phase atoms have been purely of a van der Waals nature, so 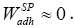
According to Mukhopadhyay and Schreiber [23] the work of adhesion has been coupled to ΔG via the following dependency:
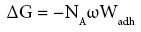 (12)
(12)
Whence, letting Eq. (11) in Eq. (12) and regarding Eq. (10) lead to the Schultz dependency [21]:
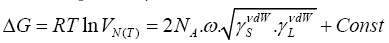 (13)
(13)
It would be necessary to add that Goss approached the problem of derivation of the Eq. (13) taking the interactions between the surfaces of two bulk phases into account [13].
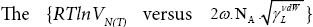 dependency encompases properties both the probe and the tested material, and simultaneously for a homologous series of n-alkanes gives a non-linear fit for LCSPs. Its gradient yields the value of the van der Waals component of the surface free energy
dependency encompases properties both the probe and the tested material, and simultaneously for a homologous series of n-alkanes gives a non-linear fit for LCSPs. Its gradient yields the value of the van der Waals component of the surface free energy 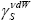 [20,21].
[20,21].
The IGC tests of the LC phases pertaining to nonspecific, 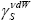 , contributions of the surface free energy of adsorption and solution are relatively few in the available literature.
, contributions of the surface free energy of adsorption and solution are relatively few in the available literature.
Thus, it can be argued that the acid-base interactions require the presence of both acidic or electrophilic (electron-accepting) and basic or nucleophilic (electron–donating) species. From the ‘IGC point of view’, viz., in the case of a dilute probe interacting with a LC molecule, if the probe has electron-accepting properties so the donor properties of the LC tested could be probed, while if the probe has electrondonating properties it could be probed as the acceptor properties of the LC tested.
To characterize the tested chromatographic system from the acceptor-donor point of view, the free energy of adsorption is usually determined. Brookman and Sawyer are the first, who suggested a conceptually convenient approach to consider the total free energy of adsorption, ΔGads, as a sum of several sources of different interaction [29], which can be widened for mesophase, i.e. ΔGdis:
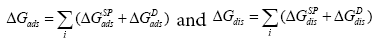 (14)
(14)
The specific interaction summation, 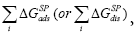 includes all possible sources of interaction other than the nonspecific (dispersive) one,
includes all possible sources of interaction other than the nonspecific (dispersive) one,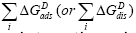 Such effects as acid-base interaction, dipoledipole interaction, induced dipole-dipole interaction, hydrogenbonding forces, π-character and steric effects are included in the specific interaction section [30]. In this context it is necessary to emphasise the Fowkes’ statement that hydrogen bonds are a sub-set of the Lewis acid-base interactions, in which the ‘active’ hydrogens are the acid sites, i.e., electron-accepting sites [31]. Mulliken was the first to characterise the acid-base interactions as charge-transfer complexes, in which there are two contributions to the energy of interaction, i.e., electrostatic and covalent [32]. Ratajczak and Orville-Thomas have concluded that fundamentally there is no difference between ‘hydrogen bond’ and ‘charge transfer’ interactions [33]. According to them, the hydrogen bond may be considered as a specific type of electron donor-acceptor interaction which is within the medium of the range of strong interactions. Care has to be taken not to ignore any of these interactions.
Such effects as acid-base interaction, dipoledipole interaction, induced dipole-dipole interaction, hydrogenbonding forces, π-character and steric effects are included in the specific interaction section [30]. In this context it is necessary to emphasise the Fowkes’ statement that hydrogen bonds are a sub-set of the Lewis acid-base interactions, in which the ‘active’ hydrogens are the acid sites, i.e., electron-accepting sites [31]. Mulliken was the first to characterise the acid-base interactions as charge-transfer complexes, in which there are two contributions to the energy of interaction, i.e., electrostatic and covalent [32]. Ratajczak and Orville-Thomas have concluded that fundamentally there is no difference between ‘hydrogen bond’ and ‘charge transfer’ interactions [33]. According to them, the hydrogen bond may be considered as a specific type of electron donor-acceptor interaction which is within the medium of the range of strong interactions. Care has to be taken not to ignore any of these interactions.
Fowkes presented the concept of hydrogen-bonds and acid-base interactions at liquid solid interfaces [30,31]. According to him, if chloroform as an acid and a polycarbonate surface as a basic, a strong interaction occurred, but there was no acceptor-donor interaction within chloroform or within polycarbonate. Liquids can also be characterised by donor, DN, and acceptor, AN, numbers following the Gutmann acid-base approach [34]:
1) The donor number characterising the basicity or electrondonor ability,which is the molar enthalpy value of the reaction between the base, viz., the electrondonor D and a reference acceptor, antimony pentachloride -SbCl5 , in a dilute solution of 1,2-dichloroethane;
2) Whereas the acceptor number characterising the acidity or electron-acceptor ability, which is defined on the NMR chemical shift of 31P in triethylphosphine – (C2H5)3PO, when it is dissolved in the acceptor solvent A.
In chromatographic studies of acceptor-donor properties, it is necessary to choose either a strong donor (base) character or a strong acceptor (acid) character.
The donor number (DN) was defined by Gutmann [34] as the negative enthalpy of the formation of the adduct being the Lewis base reacted with the reference Lewis acid, SbCl5 :
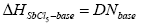 (15)
(15)
It is necessary to mention that Gutmann has also introduced the concept of an acceptor number (AN) to measure the strength of the Lewis acidity or electrophilicity of a liquid [34]. The ANvalues have been determined from the magnitude of induced chemical shifts in 31P NMR spectra of triethylphosphine oxide (C2H5)3PO) as a basic probe [34]. In this way, both AN and DN values were scaled semi-empirically, and a given acceptor-donor interaction could be expressed as the following dependency:
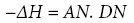 (16a)
(16a)
being an analog to the E and C equation [35]:
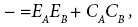 (16b)
(16b)
where: ΔH - the enthalpy of adduct formation for the acceptordonor pair,
EA and CA the empirically determined parameters and assigned to each acceptor,
EB and CB the empirically determined parameters and assigned to each donor.
Generally, the C parameters represent the covalent contributions and the E ones those arising from the electrostatic interactions between the acceptor and the donor components of the adduct.
Gutmann also characterised liquids by donor, DN, and acceptor, AN, numbers. Therefore, an attempt to characterise the acceptor acidic and donor basic properties within the mesophases, i.e., smectic B and nematic, on the basis of the 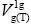 values seems to be pertinent to the most characteristics of LCs within their mesophases.
values seems to be pertinent to the most characteristics of LCs within their mesophases.
The main advantage of Gutmann’s donor and acceptor concept is that it recognises the bi-functionality of substances, however, it is not convenient to distinguish between hard and soft contributions to acceptor-donor behaviour.
The simplicity of the AN and DN concept has made it particularly attractive for use in the characterisation of acceptor-donor interactions for the diversity of liquid crystals relevant to chromatographic stationary phases. Riddle and Fowkes [36] have conducted surface tension measurements and succeeded in correcting Gutmann’s original AN values for many liquids by the incorporation of van der Waals contributions. They have provided for AN the same thermodynamic units as DN. According to Ma et al. [37] introduced a factor to normalize both scales by:
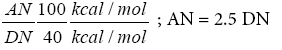 (17a)
(17a)
in order to turn the DN values into a dimensionless number.
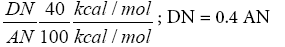 (17b)
(17b)
Kitaura and Morokuma [38], and Lee [39] explored the scope and limitations of the acceptor-donor interaction in the formation of an interfacial bond, i.e., the concept of the acceptor-donor interaction to solid adhesion. According to them the overall nature of the acceptordonor interaction consists of electrostatic, ΔEes, charge or electron transfer, ΔEct, exchange, ΔEex, polarization, ΔEpo, and coupling terms of a higher order, in some cases including the dispersion component of Lifshitz-van der Waals (LW) forces, ΔEmix, and can be expressed via the so-called perturbation equation [38,39]:
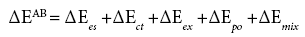 (18)
(18)
Isaacs suggested that the electrostatic interaction energy is the Coulombic interaction, which involves permanent charges, dipoles and higher multi-poles present in interacting respective molecules [40]. Therefore, the overall result could be attracting or repelling. Whereas, Lee wrote that the electrostatic energy is the energy of interaction between undistorted charge distributions of two closed-shell molecules [39].
Van Oss et al. suggested in their method, that interfacial acceptordonor interaction requires that acceptor sites of one phase interact with donor sites of the other, so that if either phase is neutral or if both phases have only basic or only acceptor sites, there can be no acceptordonor interaction [27].
Among the applications of the IGC to test liquid crystals one of keen interest to users is the elucidation of the acceptor-donor properties. In order to assess the acceptor-donor characteristics of solid surfaces by the IGC method, it is necessary to study the specific interactions between the surface tested and two references polar ‘molecular probes’, i.e., an electron donor (Lewis base probe), DN, and an electron acceptor one (Lewis acid probe), AN. The Gutmann theory specifies the magnitudes of AN and DN [34], however, they do not lead to direct designations in the IGC tests. Lara and Schreiber have adopted the following arbitrary criteria for both, namely the free energy of adsorption,  and the free energy of dissolution,
and the free energy of dissolution,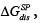 which for the solid surface are expressed in the following ways [41]:
which for the solid surface are expressed in the following ways [41]:
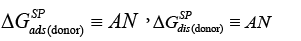 (19a)
(19a)
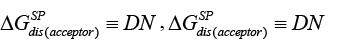 (19b)
(19b)
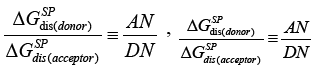 (19c)
(19c)
They have also proposed the arbitrary acceptor-donor scale [41]:
 (20a)
(20a)
 (20b)
(20b)
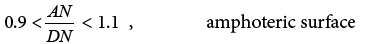 (20c)
(20c)
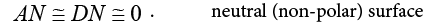 (20d)
(20d)
The total free energy of a specifically interacting mole of probe vapour with the functionalised surface of the liquid-crystalline stationary phase (both solid and liquid) can be expressed in a threefold way as the equations 1-3 based on the underpinning chromatographic values, i.e., specific retention volume, 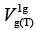 [3,4].
[3,4].
The serious drawback of this methodology is that the specific contribution of the free energy of adsorption and dissolution cannot be separated unambiguously from other contributions. However, many physicochemists show a keen interest in the deep characteristics of ‘liquid-crystalline materials’ properties. The IGC is just one of the methods which facilitate it. Whence, the relationships between different chromatographic data on one side and the phenomenological parameters of the donor and acceptor properties of the LCSPs on the other will be determined throughout this paper.
The specific interactions correspond to the sum of acid, base and hydrogen bond interactions. The aforesaid interactions can be quantitatively characterized by the KA and KD parameters. The KA and KD values have usually been determined by employing the following dependency:
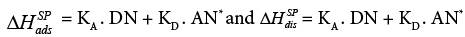 (21a)
(21a)
The energy values pertaining to the specific enthalpy of adsorption of the probe on the tested surface, 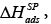 can be determined by employing the following dependency:
can be determined by employing the following dependency:
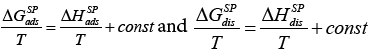 (21b)
(21b)
The values of the KA and KD parameters calculated in this way are theoretically independent of the column temperature, however, Cava et al. [42] have suggested that in practice the temperature can change the acidity and basicity of the tested solid and liquid as well.
Apart from that, Voelkel described in his paper another method of determining the KA and KD and D K parameters by the direct use of the 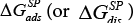 value, which introduces the contribution of the entropic term [43] and can be expressed as:
value, which introduces the contribution of the entropic term [43] and can be expressed as:
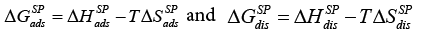 (23a)
(23a)
Thus the equation (23a) has taken the following form:
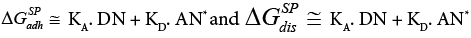 (23b)
(23b)
where 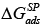 and
and 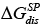 are the specific components of the free energy; actually it is the vertical distance between the total free energy of the polar probe and the total free energy of a hypothetical n-alkane on the reference line having the same value on the abscissa, denotes the donor number in the Gutmann scale [34], and AN* the acceptor number in the Riddle-Fowkes scale [36].
are the specific components of the free energy; actually it is the vertical distance between the total free energy of the polar probe and the total free energy of a hypothetical n-alkane on the reference line having the same value on the abscissa, denotes the donor number in the Gutmann scale [34], and AN* the acceptor number in the Riddle-Fowkes scale [36].
In this paper the research effort has been focused on the characterisation of the donor-acceptor properties of different LCSPs by the comparison of different methods for obtaining and refining the results [44].
Çakar and his coworkers tested chromatographically the acceptordonor properties of
1. 4-[4-(2-ethylhexyloxy)benzoyloxy]benzoic acid (EBBA) [45,46]:
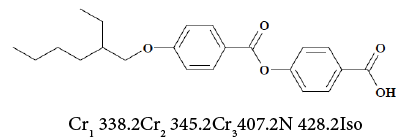
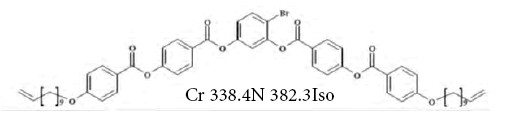
2. 4-bromo-1,3-phenylene-bis[4-[4’-(10-undecyloxy)- benzyloxy]]benzoate (BPUBB) [44]:
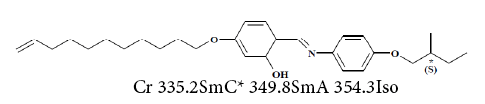
3. (S)-4(undec-10-enyloxy)-2-hydroxybenzylidene-4-(2- methylbutoxy)aniline(UMBPIMP) [44,47]:
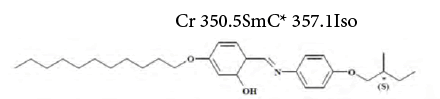
4. (S)-4-(dodecyloxy)-2-hydroxybenzylidene-4-(2-methylbutoxy) aniline (SALC) – schiffbase [44,48]:
5. (S)-4-(5,5,6,6,7,7,8,8,9,9,10,10,10-tridecafluorodecyloxy-2- hydroxybenzylidene-4-(2-Methylbutoxy) aniline (SFSALC) [44,48]:

The thermodynamic properties of UMBPIMP were investigated in order to understand in depth the interactions between the liquid crystal and different probes for its further exploitation. Therefore, then the Flory-Huggins polymer-solvent interaction, 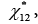 hard-core polymersolvent interaction,
hard-core polymersolvent interaction, 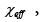 and exchange parameters such as effective energy,
and exchange parameters such as effective energy, 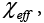 enthalpy χ12 and entropy, χ S, for the probes employed were determined and discussed [47].
enthalpy χ12 and entropy, χ S, for the probes employed were determined and discussed [47].
The values of the dispersive component of the surface free energy, 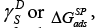 the specific free energy of adsorption,
the specific free energy of adsorption,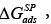 the enthalpy of adsorption,
the enthalpy of adsorption, 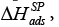 the entropy of adsorption,
the entropy of adsorption,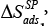 of neutral, acidic, basic and amphoteric testing substances were employed for the testing of both LCs. Then
of neutral, acidic, basic and amphoteric testing substances were employed for the testing of both LCs. Then 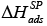 magnitudes were correlated with the Gutmann’s modified acceptor, AN*, and donor, DN, numbers for the testing substances with the aim to quantify the values of the acid, KA, and basic, KD, parameters of the LCs surfaces.
magnitudes were correlated with the Gutmann’s modified acceptor, AN*, and donor, DN, numbers for the testing substances with the aim to quantify the values of the acid, KA, and basic, KD, parameters of the LCs surfaces.
The specific case of LCs constitute ‘bent-core’ molecules. One of them is 4-bromo-1,3-phenylene-bis[4-[4’-(10-undecyloxy)- benzyloxy]]benzoate with the nematic mesophase ranged from 65.2 to 109.1°C [46]. The tests of the acceptor-donor properties of the BPUBB compound were performed within the column temperature range 35- 60 °C, by employing nonpolar, polar and amphoteric testing substances. The IGC tests were performed at the infinite dilution conditions of probes. The dispersive component of the surface free energy, 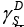 or
or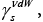 for the LC tested was determined for nonpolar organics. The values of the specific enthalpy of adsorption,
for the LC tested was determined for nonpolar organics. The values of the specific enthalpy of adsorption, 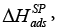 were determined and correlated with both the donor and the acceptor numbers of the probes used to quantify the acid KA and basic KD parameters of the LCSP surface [46]. The values of the KA and KD parameters were found to be 0.033 and 0.316, respectively, and the ratio of the
were determined and correlated with both the donor and the acceptor numbers of the probes used to quantify the acid KA and basic KD parameters of the LCSP surface [46]. The values of the KA and KD parameters were found to be 0.033 and 0.316, respectively, and the ratio of the 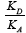 quotient between 35 and 60 °C was equal to 9.63; it meant that the BPUBB surface exhibited a basic character.
quotient between 35 and 60 °C was equal to 9.63; it meant that the BPUBB surface exhibited a basic character.
The acceptor-donor and surface characteristic of SALC and SFSALC liquid crystals were performed on the IGC results. Seeing that the values of the KA and KD parameters for the SALC compound were found to be equal to 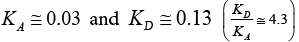 [48]. Whereas, the values of the KA and KD parameters for the SFSALC compound were found to the Fowkes approach
[48]. Whereas, the values of the KA and KD parameters for the SFSALC compound were found to the Fowkes approach 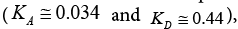 to the Dong approach
to the Dong approach 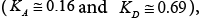 regarding decadic log of vapour pressure
regarding decadic log of vapour pressure 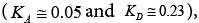 the boiling temperature (
the boiling temperature ( 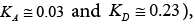
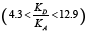 [47]. Regarding these values, the surface of the SFSALC exhibited a more basic character than that of SALC between 303 and 323 K [48]. According to the afore-mentioned authors this can be explained by the high 12 electronegativity of the of the fluorine atoms forming the hard C-F dipoles which are strong polar, hydrophobic in nature, and weakly polarisable [48].
[47]. Regarding these values, the surface of the SFSALC exhibited a more basic character than that of SALC between 303 and 323 K [48]. According to the afore-mentioned authors this can be explained by the high 12 electronegativity of the of the fluorine atoms forming the hard C-F dipoles which are strong polar, hydrophobic in nature, and weakly polarisable [48].
In the Ocak’s et al. article was described that the retention times were determined at 373.2 - 398.2K [49]. However, the dispersive surface free energy,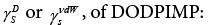
5-((S)-3,7-dimethyloctyloxy)-2-[[[4-(dodecyloxy)phenyl]imino] methyl]phenol , was determined by the methods of Schultz and Dorris- Gray for the temperatures 303.2, 308.2, 313.2 and 318.2K, 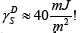 The phase transition Cr-SmC* of the DODPIMP compound is equal to 326.4K. Thus, these tests were performed only for crystalline. Whereas the value of the
The phase transition Cr-SmC* of the DODPIMP compound is equal to 326.4K. Thus, these tests were performed only for crystalline. Whereas the value of the 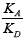 quotient was equal to ca. 10.6, i.e. basic character of surface [49].
quotient was equal to ca. 10.6, i.e. basic character of surface [49].
Taking into account the physicochemical background and review of the literature concerning chromatographic studies of non-specific and specific properties of liquid crystals, it can be stated that they were tested only as crystallines, viz., the values the 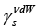 parameter and the
parameter and the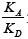 ratio were not determined for liquid crystals’ mesophases. That is why our aim is to present the need for the characteristics of the energetic properties of the LCs in mesophases.
ratio were not determined for liquid crystals’ mesophases. That is why our aim is to present the need for the characteristics of the energetic properties of the LCs in mesophases.