In phase II clinical trials, multiple competing treatments are under the study. Vast literature exists on how to allocate the incoming patients to one of the treatments rationally, leading to various optimal trial designs with different optimality criteria under different design scenarios. In some situations, the covariates of incoming patients are known, this information can be incorporated into the design to improve the efficiency of the trial. A main consideration in such design is to balance the covariates in allocating patients to treatments while maintaining randomization. However the two objectives often conflict. Also, as in typical phase II clinical trial the sample size is not large, when there are multiple covariates to account for, the balance is difficult or impossible to achieve.

This article is motivated by the design of a novel stroke rehabilitation trial: the Critical Period After Stroke CPASS--Critical Period After Stroke Study. Study conducted at Georgetown University and MedStar National Rehabilitation Hospital. Currently factors contribute to stroke recovery is understood by at least two mechanisms. One is the improvement in motor, sensory and cognitive functions, and the other is through rehabilitation. Investigations by Biernaskie et al. (2004) [1] and others in animals suggest that the critical periods in stroke recovery do exist in adult mammals. However, whether and how the important results apply to human stroke patients is unknown. This trial is designed to find the critical period where motor recovery is the greatest based on several preliminary studies [2,3]. The primary endpoint is the Action Research Arm Test (ARAT) score. The known important covariates include age, gender, NIH stroke scale, time from stroke onset to baseline evaluation, concordance, etc. Patients will be assigned into three treatment arms representing three points after stroke: early (initiated within one month), outpatient (2-3 months) and chromic (6-9 months) and a control group. This sample size of 64 subjects is determined based on demonstrating a moderate effect size in the primary endpoint (ARAT score) with 80% power at a significance level of 5%, and a nominal significance level of 0.01 for one interim analysis using adaptive group sequential approaches [4-6]. The 64 subjects are to be assigned into 4 arms equally and there are five covariates to balance across the 4 arms. If a complete randomized procedure is used, sometimes it is possible for one group to receive all young patients, while another group may get all older patients. On the other hand, if an optimal design is used, it will balance the covariates among all the groups, but such procedure is often deterministic for trials with relatively small size, and more than two covariates. Thus it would be desirable to seek a semi-random, sub-optimal procedure which partially balances the covariates among groups while retaining partial randomness among the patients. Indeed, there is extensive literature of phase II clinical trial design in presence of covariates [7]. However, very little theoretical work has been done on statistical properties of various designs. Generally, full balance among covariates is not possible. Some methods are optimal but non-random, some are random but not fully optimal. To our knowledge none of the methods are uniformly superior, and in fact, there is no established statistical method to best reconcile the needs for balanced covariates and proper degree of randomization. McEntegart [8] concluded that there is little difference in power between minimization/maximization method and stratification. Hammerstrom [9] found by simulations that covariateadaptive random- ization does not significantly improve error rates, and is useful only for cosmetic purposes. Pocock and Simon [10], Klotz [11] and Titterington [12] considered a maximum entropy method, in which the entropy is defined for the probability vector of assigning the treatments to patients, and the maximization is subject to a set of imbalance constraints over strata, typically classified based on covariate. The method requires subjective inputs: the classification of the covariates into stratum, the number of stratum, and the definition of the imbalance measure. When the number of covariates is relatively large, or with continuous covariates the number of stratum can be large, and these methods are not useful. Pursuing the idea in Silvey [13], Atkinson [14] proposed an optimal trial design with covariates where (say) there are k treatments, n subjetcs and m covariates. Let R be the n×m matrix of the covariates, x be a 0-1 valued n×k matrix, each x represents a de- sign: x_ij=1 if and only if the i-th subjects is assigned to treatment j; Let X=(x, R), n×(k+m) matrix, and

M (x)=X’X

Recall that M (x)^-1/n is the covariance of the LS estimate of the corresponding linear regression model. The optimal design in Atkinson is

x_opt=arg max_x |M (x)|

This method avoids subjective inputs such as dichotomizing the covariates into stratum and defining an imbalance measure for the covariates. Allocation procedure is derived by minimizing the covariance matrix of the estimated regression parameters in the corresponding linear model. However the procedure does not aim to balance covariates across treatments, which can be problematic in phase II trials with moderate sample sizes and more than two arms.

Therefore, motivated from the stroke recovery study described before and the work of Atkinson [14], this article proposes a design in the presence of covariates which aims to balance covariates and retain randomization. We propose to use empirical likelihood to assign weights of covariates and then derive the design by balancing their (empirical) entropy, which measures the disorder, or evenness, of a system. The proposed method uses all the information in the covariates, as compared to methods using only the main covariates or their principal components. Our method maximizes, over all designs, the empirical entropy, formulated from the design and the covariates. Since the larger the entropy is, the more evenly patients are assigned along with the covariates, our method has an intuitive interpretation in balancing the covariates in treatments assignments. This method is simple to use without subjective stratification of the covariates, without choosing the imbalance measure. It is also different from those in Klotz [11] and Titterington [12] in rationale, in that we are optimizing the entropy of the assignment matrix while they maximizing the entropy of allocation probability, both subject to suitable constraints. In addition, our method does not need to stratify the covariates nor to impose an imbalance measure. The proposed resulting multi-arm design is then used further to construct the optimal and minimax design in the presence of covariates for the two-stage trial. Wason et al. [15] proposed a multi-arm optimal two-stage design for quantitative responses without covariate information. Their work extends the twostage single arm trial design of Stallard [16] to multi-arm trials, which in turn, extends the optimal two-stage design of binary responses of Simon [17] to the case of quantitative responses from multivariate normal distribution. There is a large amount of literature on two or more stage clinical trial designs. Thall et al. [18] proposed two-stage design for testing and selection of comparative clinical trials, Xiong [19] and Tan et al. [4] proposed and studied multistage designs used on sequential conditional probability ratio test procedures. Sydes et al. [20] addressed some common issues in multiarm multi-stage clinical trials, Wassmer [21] considered sample size determination in multiarm confirmatory adaptive design. Jennison and Turnbull [22] give a systematic introduction of methods in this field. Here our setting is different, we first assign the patients to multiple treatment groups based on their observed covariates, then design the sample sizes for two stages based on binary responses.

From the motivating trial, we formulate problem statistically. There are k treatments, N patients with observed covariates,

x_i=(x_i1, ..., x_id)’ of the i-th patient,

where the number of subjects N is not large, as is typical for phase II clinical trials, and the number of covariates d is typically greater than 2. Therefore as described earlier it is impossible to fully balance the covariates among the treatments and at the same time randomization. The goal is to allocate the subjects to the k treatments according to the covariates of each subject adaptively, each treatment with n=N/k subjects, while balanc ing the covariates among treatment groups and at the same time randomization, in some (sub) optimal way. Denote

X_n=(x₁, ..., x_N )’

be the matrix of all the covariates. We propose to use the empirical likelihood method to formulate the weights for each observation.

The early use of empirical likelihood (EL) can be traced back to Thomas and Grunkemeier [23], but the works of Owen [24,25] formally established the advantages and the scopes of application of this method. Since then EL has gained increasing popularity, due to its wide range of applications, simplicity to use and flexibility to incorporate auxiliary (or side) information. Qin and Lawless [26] formulated this method in parametric estimation and connected it with estimating equations. Now the EL has been applied in broad areas, for examples, generalized linear model [27], survival data [28-30], nonparametric regression [31], goodness-of-fit measure [32], inference in the presence of nuisance parameters [33], econometrics [35-37], density and quintile estimations [37-39], marginal and conditional likelihood [40], and estimations using pseudo EL method [41].

We distinguish two cases, group assignment case in which we have a group of N=nk subjects to be assigned to k treatments, each group with n subjects; the second case is sequential adaptive assignments, in which subjects come into study one by one, and the assignment is one at a time.

Let Y=(y₁,...,y_N)’ be a 0-1valued N×k matrix, y_i=(y_i1,...,y_ik)’ represents the treatment assignment of the i-th patient: y_ij=1 iff the i-th patient assigned to treatment j; Let Z=(Y,X), a Nx(k +d) matrix, zi=(yi,xi) be its i-th row. Let wi=F({zi}) be the empirical mass/weight assigned to zi, and w=(w1,...,wN). The EL subject to the side information constraints g(•), with E[g(z)]=0

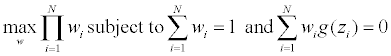
To construct non-uniform empirical weights for the observed covariates, we need some con- straints. Let J be an Nxk matrix of 1s, and 1k be the k-dimensional column vector of 1’s. Since we need to allocate each treatment the same number n=N/k subjects, let y be an iid copy of the yi’s, a natural constraint on the allocation y is g₁(y)=y −1k/k and so E[g(y)]= 0. For a constraint on the covariate x, for example we may set μ=E(x) as long as we have μ from other sources, then the constraint g2(x) satisfies E[g₂(x)]=0.

Now set g(z)=(g(y),g’(x))’, then we have E[g(z)]=0. Let tn(θ₀)=(t_N,1, ..., t_N,k+d)’ be the

Lagrange multipliers corresponding to the constraint with g(·) then

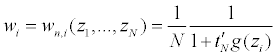
and tN,j=tN,j (z1, ..., zN ) (j=1, ..., k + d) are determined by

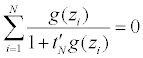
Note the wi’s are the constrained optimizers, which exist and are unique, so does t_N [42].

Let 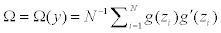As in Yuan, Xu, Zheng (2014), we have

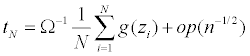
and

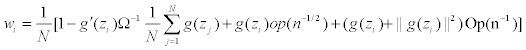
Since y follows a multinomial distribution, its covariance matrix Cov(y) is singular, and consequently, Ω is singular. In the computation we Ω⁻ as the Moore-Penrose generalized inverse of Ω, and take the approximated weights

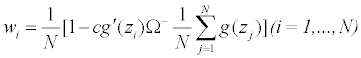
In the above, since the generalized in verse Ω⁻ is used in place of a proper inverse Ω⁻¹, the resulting weights wi=wi(c)’s may not be nonnegative for c=1, and when c=0 we get wi=1/N for all i, so we impose the constant c˜=Avg max00, then normalize the weights to make them probability weights, and still denote them as wi’s.

Based on the empirical weights wi’s, the entropy, as a function of x, is

The optimal design is y*=arg maxy HN (y), it makes the design most balanced in terms of entropy, subject to the constraint E[g(z)]=0.y* can be easily obtained via computational methods. A complete enumeration will search through all possible

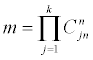
values of y’s, where C^r_n is the combination number of choosing r elements out of n.

However, y* is a deterministic procedure.

We prefer a semi-random procedure y˜ by the following step. For this, let ej be the j-th column of the k-dimensional identify matrix. Ω is approximated as

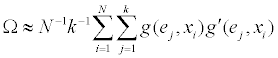
For the semi-random procedure, fix a number L

For s=1, ..., L, do the following:

a) For i=1, ..., N , sample r from uniform distribution on {1, ..., k}. If r=j, set yi=ej .

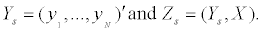
b) Compute HN (ys).

c) Set y˜=arg max ys:1≤ s ≤ L H_N (ys).

In the above procedure the proportion α=L/m controls the tradeoff between balance and randomization. If α=1 or L=m, then there is no randomization, and we get y˜=y*; if α=1/m or L=1, the procedure is completely random without optimization. Recall that the methods in Klotz [11] and Titterington [12] are also semi-random, in which when the trade-off parameter η=1, these procedures are deterministic, and when η=0, they are completely random with uniform treatments assignment without covariate effects. So they recommend intermediate values of η, and particularly for η=0.5.

The proposed method can be used in many other existing designs to incorporate the covariate information. Below we illustrate its application for the commonly used two-stage optimal and minimax design.

Now we consider the case in which the patient comes one at a time, and the corresponding patient assignment is different from the group design case. As the consideration is the initial stage of the clinical trial, the balance of number of subjects in each treatment group is of first consideration, and then is the balance with covariates among the k groups. Obviously, the first k subjects should be assigned to the k treatments, one for each treatment, at random. To weigh each treatment equally, we design the assignment in such a way that at any time the jk-th patient comes, each treatment get j subjects

Now we consider the case in which the patient comes one at a time, and the corresponding patient assignment is different from the group design case. As the consideration is the initial stage of the clinical trial, the balance of number of subjects in each treatment group is of first consideration, and then is the balance with covariates among the k groups. Obviously, the first k subjects should be assigned to the k treatments, one for each treatment, at random. To weigh each treatment equally, we design the assignment in such a way that at any time the jk-th patient comes, each treatment get j subjects.

Denote Yk=(y1, ..., yk )’ be the kxk assignment matrix of the first k subjects, the corresponding covariate matrix be Xk , and let Zk=(Yk, Xk ), a kx(k + d) matrix. When the (k + 1)-th patient comes, with covariate xk+1, there are possible assignments ej (j=1, ..., k) for this individual, denote Yk+1(j)=(ej, Yk ), Xk+1=(xk+1, Xk ) and Zk+1(j)=(Yk+1(j), Xk+1), and (k + 1)x(k + d) matrix, and Hk+1(j) be the empirical entropy based on Zk+1(j), and set

y_k+1=er, if H_k+1(r)=max H_k+1(j) 1 ≤ j ≤ k

when there is tie, we use random rule to break the tie. Therefore we assign the (k + 2)-th patient among the remaining k−1 treatments using the above method, and so on and so forth. We assign the 2k-th patient the only remaining treatment; so that in the first 2k assignments, each treatment get 2 subjects, in a partially covariates balanced way.

Atkinson’s design can also be modified this way. It requires, in addition, at least k + d initially assigned subjects, while with our method we only require at least k initially assigned subjects.

For completeness, below we derive the optimal and minimax twostage design, and the corresponding sample size determination.

In the above we studied the maximum em- pirical entropy method to incorporate the covariates into phase II clinical design, here we use the same idea to extend the existing two-stage optimal and minimax design in the presence of covariates and for multiple treatments. There are many such designs under different considerations and setups, such as the design proposed by Whitehead [43], Simon [17]’s two-stage design, the r-design the optimal design of Stallard [16], among others. We should distinguish the term “design” used in the maxi- mum empirical entropy design as given above, which means the assignments of treatments to subjects; while the same term in the two-stage design here means the selection of the numbers (N1, N2, r1, r2) to be addressed below. Here we concentrate on the case of binary response; the case of quantitative response can also be handled as in Wason et al. [15], and the r-design of Cheng and Berry [44] can also be modified to include covariates. In Simon [17]’s optimal and minimax two-stage design for binary response, no covariates is considered and there is only one treatment. Here we consider the setting with covariates and multiple k treatments, in which one treatment is under evaluation, against the other k−1 treatments. We consider the procedure with two steps. In the first step we optimize the sample sizes for each stage, namely N₁ and N₂, in the two-stage trial with multiple treatments, then in the second step, for the resulting sample size (N₁) in step one, we allocate to each treatment approximately equal number of subjects by the maximum empirical entropy method as described above for each stage.

To optimize N1 and N2 in the first step, without loss of generality we assume treatment 1 is the one under evaluation, let pj be the positive response from a patient with treatment j, g₀(p₂, ..., p_k)1(p₂, ..., p_k) be non-negative functions of the observed (p₂, ..., p_k). For example g₀(p₂, ..., p_k)=c₀(p₂ + · · · + p_k )/k and g₁(p₂, ..., p_k)=c₁(p₂ + · · · + p_k )/k with given 001<1, or g₀(p₂, ..., p_k)=min{p₂, ..., p_k} and g₁(p₂, ..., p_k)=max{p₁, ..., p_k}. In phase II clinical trial we are to test the null hypothesis H0 : p₁ ≤ min{p_1,0, g₀(p₂, ..., p_k )} versus H₁ : p₁ ≥ max{p1,1, g1(p2, ..., pk )}. In practice, often p_1,0=0.1 and p_1.1=0.3. If H₀ is accepted, the trial is terminated, otherwise it will continue to phase III for further study. Often it is required that for some pre-specified type I error (α) and power (β) (0<α, β<1), P (accept|H₀) ≤ α and P (reject|H₁) ≤ β. Since for given total sample size N and p₁ ≤ g₀, P (accept|p₁, N ) ≤ P (accept|p_1,0, N ), and for p₁ ≥ p_1,1, P (reject|p₁, N ) ≤ P (reject|p_1,1, N ), so we only need to consider.

P (accept|p_1,0, N ) ≤ α, and P (reject|p_1,1, N ) ≤ β

Phase II trials often have two stages including futility stopping, in the first stage N₁ subjects are entered, and if it is to be continued, in the second stage N₂ subjects are recruited. Since our treatment assignments depend on the covariates, and the response rates of treatments are independent, we use the maximum empirical entropy design in the last section to assign the subjects. i.e., in the first stage, assign n₁=N₁/k subjects to each treatment by this method, and if to be continued, in the second stage assign n₂=N₂/k subjects to each treatment by the method again. In the first stage the criterion should be somewhat relaxed, as the sample size is small. If the number of positive responses from treatment 1 is no more than

r₁=min {r_1,2, ..., r_1,k},

where (r_1,2, ..., r_1,k) are the positive responses from treatments 2 to k in the first stage (to be determined by the model, α, β and the optimizing procedure below), the drug is rejected; otherwise it goes to the second stage with N₂ subjects, with the maximum empirical entropy design to assign the treatments, in this stage we may put a bit more strict criterion, if the number of positive response from treatment 1 is less than.

r₂=max {r_2,2, ..., r_2,k},

where (r_2,2, ..., r_2,k ) are the positive responses from treatments 2 to k in the second stage (to be determined by the model, α, β and the optimizing procedure below) observed positive responses, then the drug is rejected; otherwise it goes to the phase III trial. For j=1, ..., k, let bj (r; p, n) and Bj (r; p, n), be the mass and cumulative distribution of Bernoulli distribution for treatment j, of r successes out of n=N/k trials with success probability p. These probabilities are independent of the treatment assignments y˜ N1 and y˜ N2. Often, the positive response rates (p2, ..., pk ) for the baseline treatments are known. We have, with

n₁=N₁/k, n₂=N₂/k and N=N₁ + N₂,

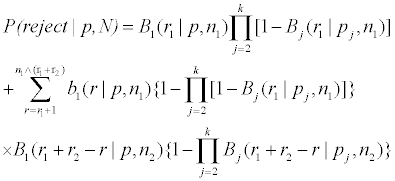
and P (accept|p, N )=1 − P (reject|p, N ). The above is an extension of the case of one treatment to the case of k treatments. Note that there are more than one (n₁, n₂, r₁, r₂)’s satisfies the constraints P (accept|p_1,0, N ) ≤ α and P (reject|p_1,1, N ) ≤ β.

Wason et al. [15] studied optimal two-stage design for quantitative responses, with- out presence of observed covariates. They assumed normal distributions for the responses; the rejection/ acceptance probability is different from those above. With the above rejection/acceptance probability we derive an optimal design in the presence of covariates and multiple treatments which minimize the expected sample size, and the minimax design, which minimizes the maximum sample size.

Optimal design

B₁(r1|p, n1) is called the probability of early termination, the expected sample size EN in the trial is

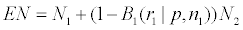
In the above, p is unknown. In the actual minimization of EN, we set p=p_1,0. If (p₂, ..., p_k ) are also unknown, we set them also to p_1,0.

As the subjects are human being, it is important that a phase II trial uses as fewer as possible the number of subjects in the study. As for the existing optimal designs for two- stage clinical trials, in the case of one treatment without covariate, the optimal phase II trial is one which minimizes the expected number of subjects for given (p₀, p₁, α, β) subject to the `two type error probabilities, with p set to p₀ . In this method, the optimal (N₁^* ,N_2^* ,r_1^* ,r_2^* ) is chosen such that

Note in the above minimization procedure, only (N1, N2, r1) enters the objective function

N₁ + (1 –B (r₁|p_1,0, n₁))N₂, and (N₁, N₂, r₁, r₂) enters the constraints P (accept|p_1,0, N ) ≤ α and

P (reject|p_1,1, N ) ≤ β. The optimal (N₁^* ,N_2^* ,r_1^* ,r_2^* ) can be evaluated by numerical methods.

Minimax design

With the two stage treatments assignments as in the optimal design case, and with the acceptance/rejection probability given there, the minimax design (N˜1, N˜2, r˜1, r˜2) follows similar way as in Simon (1989):

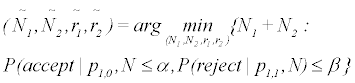
For illustration of the proposed method, below we present two simulated examples. The first is for the group Atkinson design and the proposed maximum empirical entropy design; the second is for sequential adaptive design with proposed maxi- mum empirical entropy method.

Example 1

We simulate a group design scenario similar to the real example given in the introduction, in which covariate values of N=48 patients, each with m=6 covariates generated from muti-normal distributions. We then allocate the patients to k=3, treatments according to their covariate values, using the Atkinson design and the proposed design, both with semi-random version. The results are presented in Figure 1. The first panel plots the covariate values of the patients; the second panel plots the treatment assignments for all the patients under the Atkinson design; the third panel plots the treatment assignments for all the patients under the maximum empirical entropy design. For the 2^nd and 3^rd panels, the vertical axes represent the three treatments, labeled 1,2,3; a dot in the j-th elevation indicates the underlying patient is allocated to the j-th treatment. For this example, c˜=0.15, and both designs are semi-random and sub-optimal by their own criterion.

Figure 1: Treatment assignments under two designs.

From Figure 1, we see that the covariates are quite varied, it’s not easy to pick out the few dominating variable(s), and it is impossible to balance the covariates in the three treatments in a randomized design with such a small patients size. The two designs, based on different principles, allocate the patients quite differently, however much of the difference comes from randomization, as both designs take only about 15% consideration for optimality with respect to their criterion, and 85% for randomization. It still gives us some sense of how covariates can be incorporated into the design in a sub-optimal way in such a small trial.

Example 2

Now demonstrate the sequential adaptive design with the proposed method. The setup is the same as in Example one, with three treatments and six covariates for each of 48 patients come one by one, so at the end there are a total of 48 patients. With the proposed method, each group gets 16 patients. In Figure 2, we show how the 6 covariates are distributed in the three assigned treatment groups.

Figure 2: Treatment assignments with proposed adaptive design.

Each panel displays one of the covariates of the 48 patients distributed in three assigned treatment groups, the three lines represent a given covariate allocated to the three treatment groups. From this Figure we see that the values of each covariate distributed pretty evenly among the treatment groups. Recall that the proposed method is semirandom and semi-optimal, considering the balancing of six covariates simultaneously, the result is quite reasonable.

We have studied maximum empirical entropy design for phase II multi-arm clinical trials in the presence of covariates. The method takes into the consideration both balancing the covariates among treatment groups and randomization, and is sub-optimal and semirandom. The proposed method uses all the information in the covariates, as compared to methods using only the main covariates or their principal components, and has a natural interpretation in balancing the covariates as it maximizes the empirical entropy in a proper sense. The proposed design is different from existing designs to deal with covariates. The existing methods and the proposed one have their own pros and cons, none of them is uniformly better than the others. The proposed method, like many other ones, has a trade-off between the balance of covariates and randomization, on one side it provides the flexibility for the experimenter to choose weight toward one of the factors, on the other hand this can be regarded as nonobjective. Also, like many other design methods, the proposed method has no formal theoretical justification for optimality. Our method is also implemented in the optimal two-stage phase II multi-arm trials with covariates information, and can also be implemented in other trial designs.

The research of the last author is partially supported by the National Cancer Institute (NCI) grant R01CA164717.