Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2014) Volume 3, Issue 2
The new trends in micro satellites mission for wide range of applications has motivated worldwide research in design and development of micro satellite launch vehicles (MSLVs) as a vital options in the deployment of such satellites into their respective mission orbits. Presently, most micro satellites are launched through rideshares with rockets or rocket-like systems, which were developed essentially in the seventieth and eightieth of the last century. The MSLV as a proportional micro satellite launch vehicle, up till now has only the status of technology and system study work and is well known that the research and development of MSLV are diversified in different fields. However, the realization of MSLVs is rigorous since such vehicles compound the inherent difficulties of traditional launch experiment with intrinsic problems of uneven mass distribution, slenderness, high frequency and amplitude of vibration etc. MSLV are also more likely to be affected by wind gusts and other disturbances than their conventional counterpart, and the physical parameters such as mass distribution and moments of inertia can be easily altered by changing the payload location and unpredictable propellant burning. All these factors compromise the additional velocities to overcome the aerodynamic drag, to account for steering of the vehicle and other losses. Consequently, We prototype a three stage micro-satellite launch equipment as a similitude of the European Space Agency’s VEGA launcher using a scale down derivation model and parameterized using existing VEGA launch vehicle (LV) technical data. VEGA launch data, total orbital velocity requirement including the losses and stage payload ratio are inferred and applied to the model of parameterization of launch vehicles through coupledparameters simulations. This approach can be helpful in viability and performance insights in terms of payload mass, stage mass distribution and material properties precision and effectiveness. It can also serve as a background for the development of time optimal waypoint trajectory of micro satellite launchers.
<Keywords: Micro-electromechanical systems (MEMS); Microsatellites; Launch vehicles; VEGA
L1=Length of the first stage of the rocket
L2=Length of the second of the rocket
L3=Length of the third stage of the rocket
Ln=Length of the first stage of the rocket
mp1=Initial mass of the propellant of the first stage
mp2=Initial mass of the propellant of the second stage
mp3=Mass of the payload (parabolic nose-cone)
T1=Thrust of the 1st stage
Isp_1=Specific impulse of the 1st stage in sec
T2=Thrust of the 2nd stage
Isp_2=Specific impulse of the 2nd stage in sec
T3=Thrust of the 3rd stage
Isp_3=Specific impulse of the 3rd stage in sec
Evolving trends in technological development, e-commerce, governance and medicare urgently demand the decentralization and proliferation of space missions. This call is further intensified by the need for continuous high resolution information to address some of the emerging challenges of the new world. These include terrorism, natural disasters and resource scarcity. A timely and effective response to this quest is high frequency deployment of dedicated satellites into space. To this end, advances in nanotechnology and micro-electromechanical systems (MEMS) have led to the emergence of microsatellites [1]. Ironically, launch equipment are not shedding weight and cost at a rate commensurate to their payloads. Therefore, satellites have to aggregate before making their trip to space. In view of this challenge, concerted efforts are ongoing in aerospace research and development communities to develop robust and cost effective microsatellite launch vehicles. On this basis, demand for launches has been growing steadily as people discover that continuous devolution in sizes of orbiting satellite can still handle missions previously performed by much larger satellites. The success and effective deployment of such Satellites into orbits however depends on the elements of space transportation such as ground based Launch vehicles.
Whatever the previous specifics method of deploying previous micro satellites to orbit, the natural continuation of research and development in the areas of micro satellites platforms requires vigorous complementary development in safe, affordable and sustainable launch vehicles, that is to say, the launch vehicle must be matched to the micro satellite mission if costs are to be minimized. Excess launch capacity beyond prudent margins represents wasted costs.
Recognizing that the move toward micro satellites has places added emphasis on the costs and availability of appropriate launchers, many aerospace industry as indicated in Table 1 now placed emphasis on the development of micro launch vehicles tailored specifically to meet this growing market segment.
| Vehicle Name | Organization (Country) | Max Payload Capacity (LEO) | Development Status | Target User/Buyer Markets |
|---|---|---|---|---|
| Alderbaran | CNES, DLR, CDTI (France,Germany,Spain) | Up to 300kg | Concept Study | Non-commercial, government science and tech. demo missions |
| Microsatellite Launch Vehicle | Canadian Space Agency (Canada) | Up to 150kg | Market Study | |
| Multipurpose Nanomissible | U.S Army Space and Missile Defence Command (United States) | Apx 23kg | In design phases | U.S. Government military payloads, operationally responsive space |
| Neptune 30 | Inter orbital Systems (United States) | 30kg | In development | CubeSats, universities and non-profits |
| Scorpius/Mini-Sprite | Microcosm Inc. (United States) | 22kg | Design | 1) U.S. Military and operationally responsive space 2) U.S Civil Government 3) Educational Organizations |
| Nano-Launcher | IHI Aerospace, USEF, CSP Japan (Japan) | 100kg | Concept Study | Academia and government missions |
| Virgin Galactic Micro Satellite Launch Vehicles | Virgin Galactic (United States) | 100 kg | Indevelopment | Science Missions |
| NA | NASA NanoSat Launch Challenge (United States | > 1 kg, twice in one week | Innovation Prize | Cubesats |
Table 1: Characteristics of Prospective Microsatellite Launch Vehicle and Operators.
The biggest challenge of MSLV project is development time and cost. To provide solution to these challenges, one requires unified and monumental efforts in all the major engineering fields. In addition to having an actual launch vehicles, one needs excellent instrument to provide sensor measurements, control actuators to steer the system and algorithms to process the errors and run the control loops. In order to develop the algorithms one also need testing frameworks and some kind of simulation of flights to debug the onboard algorithms. The dimension challenges, layers of dynamics complexity associated with MSLV and the potential of an improved vehicle dynamic model based on a combination of physical laws and empirical data serves as motivation of this study.
Within the framework of this study, we considered a three-stage rocket, using the VEGA rocket as a basis to set the dimensional, wind tunnel, flight parameters and dynamic properties model. The parameterized MSLV is tailored for missions to low Earth orbits and qualified to launch satellites ranging from 10 kg to 20 kg. As a rule, these are low cost satellite missions conducted by research organizations and universities for Earth observations, as well as spy, scientific and amateur mission concepts.
Realistic parameterization of MSLV is necessary condition for detailed design of new launch vehicle in loads analysis, trajectory design and guidance navigation and control mechanization. Two approaches i.e. clean-sheet method and derivatives from existing launch vehicles are commonly employ to design a new launch vehicle system [2]. In this study, constraints budget availability, low cost and the desire for a rapid development preclude clean-sheet method and derivatives of existing conventional launch systems were implemented. The proposed selected architecture of model development of MSLV is derived from existing launch systems that possesses the following attributes:
• Multistage,
• Expendable or partially reusable,
• Solid Propellant powered Rockets in all stages,
• Carries all of its required propellant from liftoff, and
• Takes off vertically with no assist from ground-based thrust augmentation.
With these features selected, we parameterize three-stage 2(10 kg) payload capacity micro satellite launch vehicle designed for Low Earth Orbit (LEO) from VEGA Launch Vehicle. VEGA Launch vehicle was developed by the European Space Agency and made its maiden voyage in 2012. Vega is lightweight three-stage all-solid launch vehicle with an optional liquid fueled upper stage for re-start and precise injection capability (fourth stage not considered here). It is designed to launch micro payloads 300 to 2,500 kg satellites for scientific and Earth observation missions to polar and low Earth orbits [3]. VEGA launch vehicle performance data for circular orbit mission with different inclination and altitudes between 300 km 1500 km are presented in figure. The three-stage MSLV employs same specific impulses similar to VEGA, but different structural ratio because of its slender nature which require more rigidity. In the aspect of stage payload ratio of VEGA used for MSLV, The second and third stages’ payload ratios are 1.2 and 0.419 times, respectively, than that of the first stage.
In order to use total orbital velocity requirement and payload mass capacity to parameterize MSLV, we modified the Konstantin Tsiolkovsky equation and its corollaries. Real rocket equations accounting for losses can now be are expressed as [4]
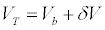 (1)
(1)
On this basis, we model preliminary mass estimator for three stages MSLV designs so that speeds required for placing micro payload into desired orbit Vb on MSLV can be achieved. The orbital velocity requirement to be delivered by the rocket for a given mission including all the losses due to gravity, atmospheric drag, propulsive losses due to the maneuvering and static pressure difference at the nozzle exit and velocity gain due to launch site Vi [5] can be stated as:
 (2a)
(2a)
 (2b)
(2b)
Where:
 (3a)
(3a)
 (3b)
(3b)
 (3c)
(3c)
 (3d)
(3d)
 (3e)
(3e)
 (3f)
(3f)
 (3g)
(3g)
 (3h)
(3h)
 (3i)
(3i)
 (3j)
(3j)
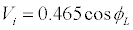 (3k)
(3k)
 (3l)
(3l)
 (3m)
(3m)
For elliptical orbit as shown in Figure 2 and considering circularization burn  out at apogee,
out at apogee,
 (4)
(4)
Each of the terms in the δV represent losses from various forces on the vehicle integrated over the flight path.
ΔVsteering is the losses due to inefficiency of the thrust vector control system for trajectory control, ΔVgravity is the losses due to gravitational forces, ΔVdrag is the losses due to fluidic retarding effect of the endoatmospheric flight acting the opposite direction of the vehicle velocity vector, ΔVearth _ rotation is losses due to earth rotation while ΔVconst are the losses during lift off, rain effect and other unknown of unknown. In addition VT is the total propulsive force from the propulsion system on the vehicle. It is the sum of the b V required to place micro satellite into desired orbit plus all the δV losses, φL is the launch site latitude, h0 is desired satellite mission altitude (circular orbit) or perigee for elliptical orbit, μ is Earth gravitational parameter, h is circularization orbit and RE is Radius of the Earth.
The drag losses are primarily depend on Rocket thrust to total rocket weight ratio (T / m(t)g ) and on the magnitude of ΔVdrag which becomes significant due to the slender nature and length of the class of MSLV.
In approach to preliminary mass estimator in this study, we consider an n -stage rocket of payload mass, mpl, stage structural mass/inert mass, mint,k, and stage propellant mass, mpr,k. Thus, the initial mass is
 (5)
(5)
and the final mass after all the propellant has been consumed is
 (6)
(6)
Where the subscript k denotes quantities pertaining to the stage of the vehicle and it is assumed here that only one stage is burning at a given time, and each stage is discarded immediately after its propellant is consumed.
Relating rocket equation of single stage to multiple stages considered here, [4] showed that the ideal rocket equation burn out velocity for a multi-stage rocket with a total of n stages can be written as follows [5]:
 (7)
(7)
With consideration that VEGA launch vehicle has accounted for all the anticipated losses and total velocity requirement is Equation. (7), we derive real rocket equations as a function of rocket mass, payload and unperturbed mission orbit as below [4];
 (8)
(8)
We use the parameter [6] of VEGA launch vehicle and ideal trajectory equation 2 to derive the total losses as follows;
 (9)
(9)
 (10)
(10)
Using the parameters of VEGA Launch vehicle from published manual and Eqs (3l,3m,4,9,10), a Simulink simulation solution was developed to infer the anticipated total velocity losses as shown in Simulink block in Figure 3 for realistic dynamics of the rocket motion.
Substituting Equation. (10) Into Equation. (8),
A real rocket equation formulation suitable for MSLV is proposed as
 (11)
(11)
In order to determine the rocket mass distribution, it is required to estimate the payload ratio λk, inert mass fraction, δk and propellant mass fraction pk, of the each stage.
The λk, δk and pk, of the each stage is therefore defined as follows [5]
 (12)
(12)
For multistage rockets considered in this study, rocket payload ratio is
 (13a)
(13a)
 (13b)
(13b)
 (13c)
(13c)
 (13d)
(13d)
Devolution of VEGA launch vehicle mass for 20 Kg microsatellites [7] payload considered in this study is modeled as;
 (14a)
(14a)
and
 (14b)
(14b)
Propellant mass of each stage is expressed as
 (14c)
(14c)
Last stage propellant mass is
 (14d)
(14d)
Mass of the empty structure after power phase for stage k
 (14e)
(14e)
Stage k initial Thrust to Weight Ratio β0k
 (14f)
(14f)
Stage k Thrust Level
 (14g)
(14g)
 (14h)
(14h)
Time duration tb,k of the power phase of stage k is
 (14i)
(14i)
Total Thrust burn time tk of the LV
 (14j)
(14j)
Instantaneous mass m0k(t) of Stage k
 (14k)
(14k)

We calculate mass distribution of MSLV based on the gross mass of each stage of VEGA LV [8] distributed as
 (14l)
(14l)
The Equations (1-14) above give proportional mass model form n-stage MSLV that can deploy a micro satellite payload to a specified burnout velocity Vb. In addition to this, mass and propulsive thrust is partition in the numerical solutions as follows:


This mathematical model is more representative of a solid-fuel launch vehicle [9] considered in this study (Figure 2). The new model formulation distributed the masses of the rocket m as the sum of dry unloaded rocket mf and the instantaneous mass of the propellants mpr(t) where m is now dependent on both time and the instantaneous distance from the nose tip to the Centre of mass of the rocket Xp.
 (15)
(15)
The distribution of mass  on three stage rocket considered in this study is shown in Figure 1 and used to
on three stage rocket considered in this study is shown in Figure 1 and used to
i=1 model the distribution of the 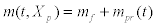
Instantaneous mass of the rocket 
The instantaneous propellant load position in the combustion chamber and instantaneous change in Centre of origin of the rocket during the burning of propellant is model as
 and
and  respectively.
respectively.
Where Xp is the instantaneous centre of mass of the rocket with respect to initial centre of mass Xicg,
Xicg(t=0) is the initial centre of mass of the full propellant load from aft end before ignition, xi is the instantaneous centre of mass of each ith stage, mmslv is the initial total lift off mass of MSLV, mmslv(t) is the instantaneous mass of MSLV during each of the stage propellant burning, mf is the mass of the dry unloaded rocket, mpr is the mass of the propellants. The launch vehicle’s full mass is calculated as the sum of all current stages with fuel in operating engines, determined in accordance with the current propulsion system’s profile of thrust.
The centre of mass of each stage is also defined as follows:



The translational equation of motion can now be re-derived by replacing m(t) with  Therefore;
Therefore;
 (16)
(16)
On this basis, the governing equations of motion on system dynamics suitable for flight of a three stage MSLV model as slender, distributed mass (Figure 4) and variable point mass with internal flow over rotating and spherical Earth is defined and can form the basis for improved mathematical models of translational motion of MSLV. The model can also reveal the effect of lumped masses on the stability of slender body with internal flow where the system has several point masses at various locations numbers.
The no dimensional rocket equation for a 3-stages rocket can thus be written as follows [4] (Table 2):
| Derived Parameters | 1st Stage K=1 | 2nd Stage k=2 | 3rd Stage k=3 |
|---|---|---|---|
| Structural Mass min, k(KG) | 7,431 | 1,845 | 793 |
Gross Mass  (KG) (KG) |
134,485 Fairing Inclusive | 38,199 | 12,448 |
Stage Payload Mass  (KG) (KG) |
38689 Fairing Inclusive | 12,448 | 1500 |
 |
0.0776 | 0.0716 | 0.0725 |
 Kg Kg |
46,120 | 14,294 | 2,293 |
 |
2.9160 | 2.6725 | 1.6196 |
 |
1.0702 | 0.9830 | 1.6916 |
 Km/s Km/s |
2.7440 | 2.8322 | 2.8910 |
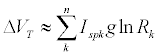 Km/s Km/s |
10.61130 |
Table 2: Derived VT Performance of VEGA Launch Vehicle using Rocket Equation.
 (17)
(17)
Where
 (18a)
(18a)
 (18b)
(18b)
 (18c)
(18c)
We then determine the relative payload ratios, αk (k=2,3) such that proportional total payload ratio, 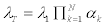 can be determine for MSLV.
can be determine for MSLV.
On the basis of VEGA Launch vehicle parameters, we use this model formulation to develop a new approach to parameter inversion of λk and total orbital velocity requirement VT from existing launch vehicle for proportional mass model of 3-stage MSLV suitable for deployment of micro satellite payload to orbit using the Equations (11-18) and parameters of VEGA launch vehicle from published manual [2].
Considering the mass distribution of VEGA [6], VEGA Rockets lass fraction at 92.6 percent propellant and 7.4 percent structure and payload are on the extreme edge of ability to fabricate, and its adaptability to MSLV due to its slender nature becomes unrealistic (Table 3). Lightweight structures made of aluminum, magnesium, titanium, and composites of epoxy-graphite are the norm for MSLV and therefore MSLV mass fraction at 85 percent propellant and 15 percent structure and payload was envisaged and considered in this study and was used to derive mass distribution as follows :
| Derived Parameters | 1st Stage i=1 | 2nd Stage i=2 | 3rd Stage i=3 |
Gross Mass  (Kg) (Kg) |
134,485 | 38,199 | 12,448 |
Stage Mass  (Kg) (Kg) |
38,689 | 12,448 | 1500 (msat) |
 Stage Ratios Stage Ratios |
0.287682 | 0.325872 | 0.120501 |
| Sigma | 1 | 1.133 | 0.419 |
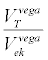 |
10611.30/2744 | ||
 |
1 | 1.03214 | 1.054 |
 |
1 | 1.13275 | 0.41887 |
 |
0.0776 | 0.0716 | 0.0725 |
 |
2.93663 | 2.78404 | 4.89070 |
 |
For α1=0.0776 α2=0.0716 α3=0.0726 |
||
 |
For α1=0.1 α2=0.1 α3=0.1 |
||
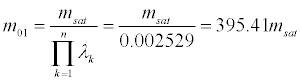 |
For α1=0.15 α2=0.15 α3=0.15 |
Table 3: Derived Mass distribution on MSLV at structural mass fraction 0.0776(VEGA), 0.1 and 0.15.
Payload=2(10 kg)
Poly-Pico Satellite Orbital Deployer (P-POD) deployment mechanism=10 Kg
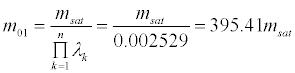
Total lift off Mass=11864.10 Kg
Plots of stages parameters distribution and bending modes are shown in Figures 5-12.
Respective plots for mass distribution (Figure 5), Natural frequency of the structural compartment at 0.15 structural mass fraction (Figure 7), bending modes (Figure 10), slopes (Figure 8) and MSLV similitude geometry of VEGA (Figure 12) is shown above using a scale down derivation models based on hybrid models of theoretical and empirical analysis and parameterized using existing VEGA launch vehicle (LV) technical data. The mass distribution plot indicate the uneven mass distribution for first, second and third stage and therefore a significant body elastic displacement during the rapid propellant burning and at the payload compartment (Figure 11 and Table 4).
| Parameters | Stage 1 | Stage 2 | Stage 3 |
|---|---|---|---|
| Gross Mass (KG) | 11864.10 | 1775.58 | 236.89 plus payload |
| Stage Mass (KG) | 10088.52 | 1568.69 | 206.89 |
| Propellent Mass (KG) | 8575.24 | 1333.38 | 175.86 |
| Inert Mass (KG) | 1513.28 | 235.30 | 31.03 |
| Thrust (KN) | 291.40 | 35.40 | 4.64 |
Table 4: MSLV Vehicle parameters.
On the basis of centre of mass formulation of equation (16), the governing equations of motion on system dynamics suitable for flight of a three stage MSLV model as slender, distributed mass (Figure 4) and variable point mass with internal flow over rotating and spherical Earth is defined and can form the basis for improved mathematical models of translational motion of MSLV. The model can also reveal the effect of lumped masses on the stability of slender body with internal flow where the system has several point masses at various locations.
Within the framework of this study, Prototype three stage microsatellite launch equipment as a similitude of the European Space Agency’s VEGA launcher using a scale down derivation models and parameterized using existing VEGA launch vehicle (LV) technical data has being developed. VEGA launch data, total orbital velocity for 250 Km orbital requirement including the losses and stage payload ratio are inferred and applied to the model of parameterization of launch vehicles through coupled-parameters simulations. This approach can be helpful in viability and performance insights in terms of payload mass, stage mass distribution and material properties precision and effectiveness. It can also serve as a system engineering platform for evaluating parameters variability on real launch vehicles, optimizing cost functions, and jump-starting achievable technologies for real implementation.