It has become evident that the USA acquisition of the position of hyper power and its dominance in the latest major conflicts is based on superior knowledge and understanding of the quantitative fundamental strategic and tactical principles of conflict and war. These include the principles of Sun Tzu, the maxims of Napoleon, and the doctrines of Clausewitz. At some time or the other these have been qualitatively expressed as slogans such as [1]:

1. Divide and conquer,

2. Get there fastest with the mostest,

3. Take the high ground.

The American military was introduced to, and has mastered Decision Theory and the Theory of Games under a mathematicallyoriented Secretary of Defense: William Perry. One particular aspect is the application of the theory developed by the English engineer Frederick Lanchester. His theory is based on the study of air battles in the First World War. It was applied in the two “Shock and Awe” campaigns against Iraq, even though initially meant to be used against the Warsaw Pact nations during the Cold War; in which its efficacy was spectacularly demonstrated.

The strategy is worthy of investigation as it is being adopted by the USA’s world competitors which is leading to new multi-players Game Theory configurations, rather than a single player situation, as can be observed in new theaters such as the Syrian conflict. The application of the theory can be expanded from defense applications to business, sports, politics and other socio-economic realms such as, dare-we-say, survival entertainment TV shows.

Expanding on a description initially suggested by Lewis [1], the concept is developed in detail, and applied to specific situations that show its potential usefulness in the context of Safeguards, Nonproliferation and Peaceful Nuclear Energy [2].

Lanchester’s model of warfare considers two opposing forces shooting at each other without any particular advantage in accuracy, weapons or force multipliers. In this case the firepower F of a fighting force is proportional to the total number of units N1 that it can muster or:

(1)

where: 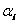is the proportionality symbol.

The units N₁ could be troops, airplanes, ships, tanks, submarines, etc. The number of targets T that a force presents to its opponent to distribute its firepower resources against is also proportional to N₁:

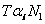(2)

Assuming also that the shooting from one side on the other follows a totally random pattern with an equal probability of scoring a hit, three important consequences of these two simple assumptions can be deduced.

First, the strength of the force S with N₁ units is proportional to both its firepower F and the number of targets T it presents to its opponent’s firepower:

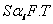(3)

Substituting from Eqns. 1 and 2 into 3, we get:

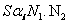(4)

Equation 4 can be rewritten as:

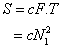(5)

where: c is a proportionality constant replacing the proportionality symbol .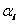

The first consequence is that the square law in Eq. 5 reveals that the strength of a force S is proportional to the square of its number of units N₁. If an army can gather twice the number of units of its opponent, its strength is not just twice its opponent’s, but the square of two or four times its opponent’s.

The implication is that it is advantageous to go against an opponent with overwhelming force or “Shock and Awe.” It also can be inferred that it pays to go with a large number of cheap units rather than a small number of expensive units. It also pays to gather allies and “coalition partners” forces and paid mercenaries, even without their being involved in the fighting; as they would draw away the fire and the losses from one’s own troops.

During World War II, the advanced-technology small number of German V2 rockets targeting London and the Messerschmitt advanced jet fighters were eliminated by an overwhelming larger number of lower-technology bomber aircraft conducting continuous day and night raids on their manufacture and launching sites. This implies the necessity of maintaining a large manufacturing and industrial base, as well as a young dynamic population base to produce that large number of unit’s base.

A constant of motion M exists that does not change as a result of the mutual fighting and the ensuing losses on both sides [1]. This constant of motion is expressed as the absolute value of the difference between the square of one’s own units 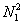and the opponent’s square of the number of units, :

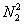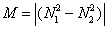(6)

The square root of M can be considered as the expected outcome O or the mean value of the remainder number of units after a confrontation:

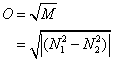(7)

The second important consequence from Eqn. 7 is that a force with a larger number than its opponent, can wipe out or exterminate the opponent while still being relatively intact.

For instance, if a force of 5 units faces a force of 3 units the expected outcome is according to Eqn. 7:

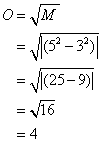
The expected outcome 4 of the confrontation is thus that the smaller force of 3 is totally wiped out losing 100 percent of its units. On the other hand the larger force would still have 4 out of 5 units left and would have lost just:

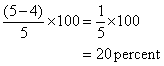
of its units.

A third important consequence of Lanchester’s law is that it provides a way for a small force to prevail over a force that outnumbers it [1]. The insight is that this can be achieved by splitting the enemy forces and dealing with their divided forces one divided group at a time; the old qualitative maxim of “divide and conquer,” penetration or concentration principle.

As a numerical example, suppose that one has 20 units confronting 25 units. A head-on confrontation according to Eqn. 7 would lead to an expected outcome of:

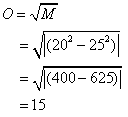
Which means that one’s inferior force would be totally wiped out, leaving 15 units of the opponents 25 units still intact. The opponent would have lost:

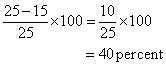
of his force, a significant loss, but would have totally wiped us out.

Suppose that by some stratagem, maybe inducing or exploiting a defensive posture by the opponent, one is able to divide the opponent’s force into two groups of 15 and 10 units each. Confronting the first group with our total force leads to the expected outcome:

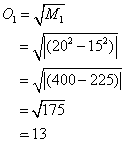
which wipes out the enemy’s group of 15, and leaves 13 of one’s troops intact. These could be used against his remaining group of 10 with expected outcome:

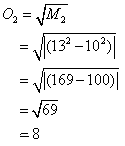
which means that an inferior force can totally exterminate a superior force while keeping:

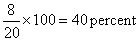
of its initial force intact.

It is human nature that people will get used and conditioned to almost anything if it goes on for long enough. The conditioning process does not take too long if it is something that people do not understand well and that they cannot experience directly.

The British military excelled at using this human cognitive feature during the period of Empire, and particularly during World War II. The British Royal Air Force (RAF) undertook a plan of disinformation to facilitate the undetected approach of a squadron of bombers to an important unspecified target in Europe. The target, possibly the hydroelectric dams in the Ruhr Valley, was so well protected that destroying it would require great surprise.

The RAF was equipped to electronically jam the existing radar at the time along the route to the target. However, the jamming by itself is an alert the defending forces. The smart approach was to condition, train, and misinform the defending German personnel into believing in something that was not true. The intended German personnel were operating novel and unreliable electronic equipment. The operators were trying to interpret radar signals without the benefit of direct observation.

This is how the RAF proceeded: at sunrise on every day, the RAF would broadcast a jamming signal for just a short period of time. On every subsequent day, just before sunrise, the jamming signal would last a little longer. The conditioning proceeded for about three months. The German radar personnel interpreted the signals their equipment gave them in just the way the British intended: They reached a conclusion that their equipment operates poorly in the atmospheric conditions present at sunrise and that the problem grows as the season progresses. The mistaken inference allowed an RAF squadron to fly undetected at sunrise far enough into Europe to reach the target and destroy it.

Multiple players’ games based on Lanchester’s Law can be envisioned, and are in fact occurring. In the case of three players game two situations arise. If the three parties are shooting at each other, the situation favors the largest force that would encourage the situation since the two other parties will be drawing fire away from it and onto each other. Eventually the smaller force is wiped out and the field is left to the two largest forces, which could settle their differences or continue the conflict to the detriment of the smaller force which would eventually be wiped out.

The second situation is an alliance of convenience where the two smaller forces ally themselves against the largest force knowing well that they would have to settle their differences after defeating the largest force.

Examples of three or more players’ games are the Serbs, Croats and Bosnians in the old Yugoslavia, and the Shiites, Sunnis and Kurds in the partitioned Iraq. An example of two forces allied against a third is the Western Alliance with the Soviet Union against Germany. It was a tepid alliance of convenience and was in fact followed by the cold war where the Soviet Union was later dismantled. In three-way contests it is logically best for two players to ally themselves against the third, such as Russia and China allying themselves against the USA.

This idealized situation can be affected by force multipliers such as superior technology, motivation, morale, weaponry, positions, intelligence gathering and even pure luck [1]. The general principles still apply. It is well known that an army surrenders not necessarily when it is defeated, but when it thinks it is defeated. It is possible to make an army perceive of defeat and surrender even it were the superior force.

Mastering these decision and game theory notions and principles is behind the present hyper-power status of the USA, obviously for as long only as its global competitors have not yet grasped them. A hyperpower dominance will eventually lead to the formation of alliances and coalitions of those who do not want to fall under its influence, against it. This explains the eventual fall and decay of the great empires throughout history. The alliances between the North Atlantic Treaty Organization (NATO) nations, the USA and the Ukraine, and the USA with Sunni Islam against Russia with Shiite Islam in Lebanon, Syria, Iran and Iraq appear to be harbingers of regrettable future conflicts.