In a recent paper in this journal, Di Vita [1] makes two separate sets of comments:

1. A critique of our joint work on a maximum entropy (MaxEnt) closure of a Galerkin principal component decomposition of a periodic flow system [2].

2. Comments on the theoretical basis of the maximum entropy production (MaxEP) hypothesis for prediction of the steady state of a flow system, advocated by a number of authors [3-7]. The latter is connected to a direct MaxEnt analysis of flow systems given by us, based on an entropy defined on the set of instantaneous flux states [8-11].

Di Vita’s first critique is incorrect, as discussed in de- tail below. Furthermore, the short qualitative discussion given by Di Vita provides a misleading picture of the very purpose of applying entropic inference to the dynamical system examined.In particular, Di Vita suggests two ad-hoc scaling transformations of the closure which the underlying Galerkin system doesnot have, and which violate the physics of a selfamplified amplitude-limited oscillation. Scaling transformations should only be applied to closures if these transformations are consistent with the evolution equation which the closures aim to characterise.

In the following, we respond to Di Vita’s comments on the MaxEnt closure of the Galerkin system and on theoretical principles, both in Di Vita A [1,12].

Response to Di Vita’s [1] critique of the scaling argument used in Noack et al. [2]. Di Vita [1] makes a scale invariance argument to criticise the analysis given in Noack and Niven [2]. However, we are afraid that he has misinterpreted our analysis. As defined in eq. (2.1) of Noack and Niven [2], ourai’s are dimensionless, representing dimensionless coordinates in a velocity phase space. Only the expansion modes have dimensions of velocity before the non-dimensionalisation. Di Vita’s argument, based on dimensions, is therefore incorrect. It is possible that Di Vita has misinterpreted our analysis in section 5, where we consider the “pseudo” dimension of each quantity, to interpret the physical meaning of the Lagrangian multipliers. We had believed that this representation was clear (and it is separate to the rest of the paper).

Response to Di Vita’s [1] choice of scaling for the maximumentropy closure of a Galerkin system [2].

In addition, Di Vita [1] questions the soundness of the maximumentropy closure of the Galerkin system [2] by imposing a curious scaling argument on the first two ordinary differential equations of the Galerkin system discussed in Noack and Niven [2,13]:

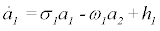(1a)

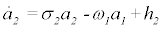(1b)

where h₁ and h₂ are higher-order terms. These two equations evidently describe an oscillator. For the post-transient periodic solution, which this study aims to approximate, the growth-rate and nonlinear terms effectivelycancel each other in a one-period average. This behavior is described and employed in numerous articles by the first author [14-16] and detailed in textbooks of oscillatory dynamics. The correspondingly filtered ordinary differential equations read:

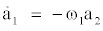(2a)

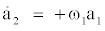(2b)

Modulo a phase shift, the solution describes the phase- invariant limit cycle with frequency ω and radius R:

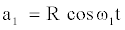(3a)

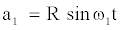(3b)

This harmonic motion approximates well (1) when the radius R is determined from energetic (or other) considerations. There exists only one non-trivial radius R for which the average power vanishes. Curiously, Di Vita imposes a parabola (!) as the scaling relationship

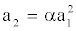(4)

The source of this relationship is called ‘dimensional argument’, but prettymuch left in the dark. He argues further that the MaxEnt closure is not invariant with respect to this imposition hence the MaxEnt closure must be flawed.

We argue that a parabola is an arbitrarilypoor approximation of a circular limit-cycle, is inconsistent with the effective phase-invariance property of the Galerkin system, and should hence not even be considered as a scaling relationship. If (4) were true, then a2 would either be always non-negative or always non-positive, violating (3a). Starting with (3b), we obtain a₂= α (1+cos 2ω1 t)/2 which is obviously incompatible with (3b). Even if the approximate solution of the Galerkin system was un-known, the equations are actively phase-invariant and mirror symmetric for a1, a₂. If a₂=αa₁² is true, then a₂=- αa₁², a₁=αa₂², etc, would be true as well, imposing a₁=a₂=0 as the only solution. However, a₁=a₂=0 is in contradiction to the assumed non- trivial limit cycle behavior. Even if the Galerkin system was not effectively phase invariant, why should a trans-formation impose a single sign on one of the amplitudes? Principal orthogonal decomposition (POD) modes should vanish on average, leading again to the unphysical solution a₁=a₂=0. Hence, the curious scaling relation-ship (4) should not be applied. Thereafter, the construed counter-argument collapses.

In addition, Di Vita also requests scaling invariance E → λE from the closure, this time without going into the analytics. Why should the MaxEnt closure be in different to arbitrary energy levels when the Galerkin solution and the resulting power equation permit only one non-trivial fluctuation level corresponding to von Karman vortex shedding? Again, a symmetry is suggested which is in contradiction to the nature of nonlinear oscillation with a stable limit cycle. Scaling arguments should only be applied to closures when the constitutive evolution equations have the scaling properties. Clearly, Di Vita’s criticism is based on a misunderstanding of the foundation of such scaling arguments.

Broader comments on theory [1,12], we also wish to raise some broader questions concerning nonequilibrium thermodynamics and the analysis of dissipative systems. Firstly, we are curious why Di Vitapays so much attention to Prigogine's [17]. MinEP principle? For a system with a unique steady state - which generally implies a system which is “near equilibrium" - this merely identies the steadystate solution in the space of transient non-solutions. The steady-state solution is usually also obtainable by direct calculation, in which case Prigogine's principle tells us nothing new. Indeed, we are unaware of any example in any branch of engineering in which Prigogine's principle is actually invoked. We here distinguish Prigogine's principle from other MinEP or related principles which have found utility in engineering, such as the MinEP engineering design principle of Bejan [18], the MinEP limit given in nite time thermodynamics [19-21] or its steady-state analogue [22], or the minimum power principle invoked in the analysis of electrical networks [23,24]. Prigogine's principle is fundamentally different to the entropy production extremum hypotheses principles of interest to us and many others, especially the MaxEP principle advocated by Paltridge [3] and its inversion to a MinEP principle by switching between ux and force constraints [25-30]. Such principle(s), if they exist, would identify the observable steady state from the set of many possible steady states. This would provide (or extract) some extremely useful information, without the need for a full dynamical solution. This utility explains the strong attention this topic has received in the literature. Di Vita [1] dismisses the existence of the Paltridge MaxEP principle on the grounds that it involves the introduction of additional hypotheses, which by themselves are less evident than [MaxEP] itself. This criticism may be correct insofar as it applies to Ziegler's orthogonality principle [31] and to early theoretical treatments of the Paltridge MaxEP principle [32,33], in which errors have been identified [34,35]. It could also be made of a recent treatment [36] in which an irreversibility function itself the consequence of MaxEnt analysis is imposed as a constraint, which might be considered to invoke circular reasoning. Di Vita's criticism could also be leveled at the various formulations of upper bound theory in turbulent uid mechanics [37-39], in which the postulated extrema may appear rather ad hoc. However, other theoretical treatments have been proposed to explain entropy production extrema, including our above mentioned MaxEnt analysis of an infinitesima low system [8-11]. The analysis is based on maximization of an entropy depend on the set of instantaneous flux states and reaction rates, giving a potential function (negative Massieu function) which is minimized at steadystate low. In certain circumstances, this can be interpreted to give rise to a secondary" MaxEP principle. We do not believe that this analysis invokes any additional hypotheses; indeed, it preserves the Legendre mathematical structure also evident in equilibrium thermodynamics. It cannot be so readily dismissed by Di Vita.

Furthermore, Di Vita [1] comments that he has criticised the first author’s 2009 paper [8] in his 2010 paper [12]. However, the only thing we can find is an oblique comment on our choice of prior probabilities, and that the analysis does not give a MaxEnt equivalent of Liouville’s equation. These comments are so vague that we do not see how to interpret them as a criticism. In the first study [8] we do adopt a uniform prior probability, but in later works [9-11] we consider a prior probability in its full generality, which must be selectedfor the problem at hand. This is a feature of all MaxEnt analyses [40]. Indeed, in the cited MaxEnt closure of a Galerkin decomposition [2,13], solution requires the use of a non-uniform prior to account for marginal stability of the fixed point of the limit cycle. The MaxEnt method is therefore tightly connected to Bayesian inference, in that it is necessary to choose (or infer) a prior probability from the problem specification. Concerning Liouville’s equation, the idea of a mechanical basis of thermodynamics is certainly very old but quite flawed, especially if the p’s and q’s are insufficient to describe the system (e.g. for interacting particles, or in dissipative systems, or in flow systems under the Eulerian description). Callen [39], for example, does not require or even mention Liouville. Even the masterful treatise by Hill [40] examines Liouville, but does not actually use it. Writing Boltzmann’s principle (“MaxProb”) [41-44] in the weak or inferential form [45]:

“A system may be inferred to be in its most probable state”,

We see that this principle applies to any probabilistic system, regardless of whether it is a thermodynamic system or involves thermodynamic equilibrium. Indeed, this principle provides the foundation of Large Deviations theory in statistical inference [45] and also of the Method of Types in communication theory. To the extent that the relative entropy function and Jaynes’ MaxEnt method are derivable from Boltzmann’s principle, they also apply to any probabilistic system regard- less of its connection to thermodynamics. We invoke this MaxEnt method of inference directly; no further dynamical principle is needed.

Other than this, we appreciate Di Vita’s 2010 paper [12] and its classification scheme. We have two major points of departure, however:

1. Di Vita assumes local thermodynamic equilibrium (LTE), a very strong assumption, which strongly constrains his results. In chemically reactive systems, especially in natural systems, we know that LTE is not correct. The analysis then becomes messy, requiring empirical kinetic rate laws with fitted parameters, but in many systems this cannot be avoided. We also invoke LTE in many of our studies (primarily to define local temperatures, chemical potentials, etc), but do not see it as critical to the analysis; we would gladly discard it if a better method were available.

2. Although Di Vita [12] gives a nice structure and some useful inequalities, expressing a number of variational principles with which to determine sys- tem stability indeed, which play the role of constraints is it enough? Are there any other principles derived directly from probabilistic inference which can be used for system closure? If such principle(s) do exist, they will one day be considered of equal status to the four known laws of thermodynamics. Indeed, they will come to define “thermodynamics” as distinct from present-day “thermostatics”.

We thank Di Vita for his interest in our work.