Forest Research: Open Access

Forest Research: Open Access
Open Access

ISSN: 2168-9776

Research Article - (2018) Volume 7, Issue 1

View PDF Download PDF

Developing One-variable Individual Tree Biomass Models based on Wood Density for 34 Tree Species in China

Zeng WS*
Academy of Forest Inventory and Planning, SFA, Beijing 100714, China
*Corresponding Author: Zeng WS, Academy of Forest Inventory and Planning, SFA, Beijing 100714, China, Tel: +923337474117 Email:

Abstract

Forest ecosystem is the largest carbon bank on land, and biomass models will be essential basis for evaluating carbon sequestration capacity of forests. Based on the general biomass model M=0.3pD7/3 presented by Zeng and Tang, one-variable individual tree aboveground biomass models for all 34 tree species or groups in China were established using the data of wood basic density of all tree species published; and based on the mensuration data of the National Forest Biomass Modeling Program, the aboveground biomass models of 14 tree species or genera were validated. Additionally, compatible belowground biomass models and root-to-shoot ratio models for two species groups, coniferous and broadleaved, were developed and evaluated. The results showed that the averages of absolute relative errors of above- and below-ground biomass estimates from one-variable biomass models developed in this study were less than the error allowances 10% and 15%, respectively. The developed biomass models here could be applied to estimate forest biomass at national level and would be important supplement to the ministerial standards on biomass models which were promulgated and implemented in the recent years.

<

Keywords: Aboveground biomass; Belowground biomass; Wood density; Root-to-shoot ratio

Introduction

In the context of climate change, information on amount of forest biomass has been paid more attention. As the main body of terrestrial ecosystem, forest ecosystem is the largest carbon bank on land, occupying about 80% aboveground biomass carbon and 40% belowground biomass carbon of terrestrial ecosystem [1]. Forest biomass is an important index of sustainable forest management, which can be used not only for evaluating the amount of bioenergy and carbon storage, and also for studying forest health, forest productivity, and nutrient cycle [2]. Forest ecosystem plays an irreplaceable role in maintaining global carbon balance and mitigating climate change. The size of contribution mainly depends on carbon sequestration capacity of forests, and biomass models will be essential basis for assessment of carbon sequestration capability [3].

Since the beginning of the eighth national forest inventory of China, the National Forest Biomass Modeling Program for main tree species has been implemented, and a lot of findings have been achieved and many papers on modeling individual tree biomass has been published [4-21]. Up to now, based on two ministerial technical standards on sample collection and methodology for tree biomass modeling [22,23], 13 ministerial standards on tree biomass models and related parameters to carbon accounting have been published [24-36], involving the following tree species or genera: Abies, Picea, Larix, Cunninghamia lanceolata, Pinus massoniana, P. yunnanensis, P. tabulaeformis, P. elliottii, Cryptomeria, Quercus, Betula, Schima superba and Liquidambar formosana. The ministerial standard for Populus has also been finished which will be published for application in late 2018. Although these 14-tree species or genera have covered nearly 70% forest resources of China, but in order to obtain accurate estimates of forest biomass and carbon storage of the whole country, we need to establish suitable biomass models for other tree species or groups involved in the remaining 30% of forest resources.

According to the findings from West et al. [37,38], the aboveground biomass of trees is mainly related to the diameter at breast height. And from the latest study by Zeng and Tang [13], the aboveground biomass of trees is highly related to wood density, and the presented general biomass model M=0.3pD7/3 has been validated to be applicable [20]. In this paper, based on the above research results, the author will: i) use the data of wood density for various tree species from published literatures [24-36,39] to develop one-variable aboveground biomass models for the corresponding tree species; ii) use the data of the National Forest Biomass Modeling Program to validate some of developed aboveground biomass models, and establish compatible belowground biomass models and root-to-shoot ratio models for two species groups, conifer and broadleaf. All the models developed in this study will provide basis for accurately estimate forest biomass and carbon storage of China in the ninth national forest inventory.

Data And Methods

Data

Data used in this paper include three parts: the first is the data of basic wood density for two hundreds of tree species published by the Institute of Wood Industry, Chinese Academy of Forestry [39], including 453 sets of data and covering information of 2687 sample trees; the second is the data of basic wood density and above- and belowground biomass for 14 tree species or genera in the published or pre-published ministerial standards, involving a total of 6023 sample trees; the third is the data of basic wood density from 138 and 100 sample trees for Cupressus and Pinus densata respectively, collected by the National Forest Biomass Modeling Program, and some related literatures [40,41].

Methods

According to the population classification on modeling single tree biomass equations for national biomass estimation in China [4], tree species of the whole country were classified into 34 groups based on the amount of stocking volume. Besides 14 tree species or genera for which ministerial standards on tree biomass models have been published or would be published in 2018, for other 20 tree species or groups only several applicable biomass models can be found in related literatures [40,41], and some of them are two-variable models which are not convenient to be used in the calculation of national forest inventory. In this study, one-variable individual tree biomass models based on wood density for 34 tree species or groups in China will be developed as follows.

Calculating mean basic wood density: According to the classification scheme of tree species by Zeng et al. [4], the following 34 tree species or groups are defined, that is, Quercus, Abies, Picea, Betula, Larix, Cunninghamia lanceolata, Pinus massoniana, Populus, P. yunnanensis, P. densata, Tilia, Cupressus, Fraxinus mandshurica +Juglans mandshurica+Phellodendron amurense, Schima superb, P. tabulaeformis, P. koraiensis, Ulmus, P. khasya, P. armandii, Tsuga, P. sylvestris var. mongolica, Liquidambar formosana, P. elliottii, Salix, Eucalyptus, Cryptomeria, P. taiwanensis, P. griffithii, Robinia pseudoacacia, Paulownia , Cinnamomum+Sassafras+Phoebe, other pines, other conifers, and other broadleaves. Furthermore, other broadleaves are classified into 2 types, hardwood and softwood, according to the Technical Specifications on National Forest Inventory. Using the data of basic wood density and numbers of sample trees for more than 200 tree species [40], the mean values of basic wood density were computed by weighting method for 34 species or groups. For the 14-tree species or genera aforementioned, the data of mean basic wood density were cited directly from the ministerial standards.

Developing one-variable aboveground biomass models: From Zeng and Tang [13], the general aboveground biomass model can be expressed as follows:

Ma=a × D7/3 (1)

where Ma is aboveground biomass (kg), D is diameter at breast height (cm), a is the parameter (a=0.3p), and p is the basic wood density (g/cm3). By multiplying the mean value of basic wood density by 0.3 for each tree species or groups, the estimate of parameter a in eqn. (1) can be obtained. To test prediction precision of the models, the mensuration data of aboveground biomass of the 14-tree species or genera were used for validation, and the relative error was calculated as follows:

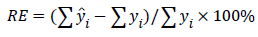equation (2)

where RE is relative error, 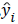equation is estimated value of biomass, and yi is observed value.

Developing one-variable belowground biomass models: Belowground biomass is usually estimated from root-to-shoot ratio model [6]. Because the stocking volume of 14 tree species or genera in the published or pre-published ministerial standards has occupied about 70% of total stocking volume in China, the belowground biomass of other 20 tree species or groups would be estimated by two types, coniferous and broadleaved species. Classifying the mensuration data of above- and belowground biomass of 14 tree species or genera into two types, compatible belowground biomass models for coniferous and broadleaved species can be developed respectively as follows:

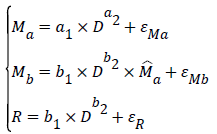equation (3)

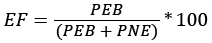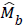where Ma and Mb are above-and belowground biomass respectively, R is root-to-shoot ratio (the ratio of belowground biomass to aboveground biomass), D is diameter at breast height, equation is the estimate of aboveground biomass, ai and bi are parameters, and εi are error items. From eqn. (3), the following belowground biomass model can be obtained: equation (4)

where equation is the estimate of belowground biomass, and we have c1=a1 × b1 and c2=a2+b2. Similarly, based on the results from eqn. (3) or eqn. (4), we can use eqn. (2) to calculate relative errors of belowground biomass estimates for conifer and broadleaf or each tree species/groups.

Results And Analysis

Aboveground biomass models

According to the aforementioned method, the mean basic wood densities of 34 tree species or groups were calculated out. For 14 tree species or genera having published or pre-published ministerial standards, the data of mean basic wood density were cited directly. Because there are no data of P. koraiensis in Institute of Wood Industry, Chinese Academy of Forestry [39], the one-variable aboveground biomass model of P. koraiensis in Chen and Zhu [40], was converted to general one-variable aboveground biomass model at the point D=16 cm, which is close to the mean diameter at breast height of all sample trees in previous work. Similarly, because there are only a few data of Tilia in Institute of Wood Industry, Chinese Academy of Forestry [39], the one-variable aboveground biomass model of Tilia was used like P. koraiensis to obtain the corresponding mean wood density and get the average values of two mean wood density [40]. The number of sample trees of Cupressus is 51, which meets the need of a large sample [39]. Considering that the data of 138 Cupressus sample trees are available from the National Forest Biomass Modeling Program, the weighted average values of two mean wood density were used here to achieve more accurate estimates. Also, the basic wood density of P. densata is the weighted average value of two mean wood density involving a total of 106 sample trees. The mean values of basic wood density and sample tree numbers of all 34-tree species or groups (other broadleaved species are further classified into hardwoods and softwoods) are listed in Table 1. Based on the basic wood density p, the estimate of parameter a in eqn. (1) can be calculated (see Table 1).

Tree species/groups Estimate of Basic wood Number of References
parameter a density p sample trees
Quercus 0.1729 0.5762 670 [33]
Abies 0.1039 0.3464 751 [30]
Picea 0.1119 0.373 901 [31]
Betula 0.1454 0.4848 690 [33]
Larix 0.1218 0.4059 602 [29]
Cunninghamia lanceolata 0.0929 0.3098 301 [28]
P. massoniana 0.1343 0.4476 301 [27]
Populus 0.1253 0.4177 901  [1]
P. yunnanensis 0.105 0.3499 150 [26]
P. densata 0.1416 0.472 106 [39]
Tilia 0.096 0.32 u [39-40]
Cupressus 0.1792 0.597 189 [39]
F-J-P 0.1392 0.464 19 [39]
Schima superb 0.1669 0.5563 150 [35]
P. tabulaeformis 0.1273 0.4243 149 [24]
P. koraiensis 0.094 0.313 u [40]
Ulmus 0.1374 0.458 27 [39]
P. khasya 0.1362 0.454 17 [39]
P. armandii 0.1179 0.393 29 [39]
Tsuga 0.1326 0.442 34 [39]
P. sylvestris var. mongolica 0.1125 0.375 22 [39]
Liquidambar formosana 0.1511 0.5035 152 [36]
P. elliottii 0.1235 0.4118 154 [25]
Salix 0.1323 0.441 29 [39]
Eucalyptus 0.1746 0.582 110 [39]
Cryptomeria 0.1048 0.3493 150 [32]
P. taiwanensis 0.1354 0.451 34 [39]
P. griffithii 0.1014 0.338 3 [39]
Robinia pseudoacacia 0.2022 0.674 25 [39]
Paulownia 0.0711 0.237 56 [39]
C-S-P 0.138 0.46 90 [39]
Other pines 0.1351 0.45 88 [39]
Other conifers 0.1182 0.394 54 [39]
Other hardwood broadleaves 0.1875 0.625 410 [39]
Other softwood broadleaves 0.1329 0.443 474 [39]

Table 1: Mean basic wood density and parameter values of the general one-variable aboveground biomass model for all tree species or groups. Note: 1) The basic wood density of P. densata is the weighted average value of two mean basic wood densities, one is 0.413 from 6 sample trees in reference [39] and another is 0.4754 from 100 sample trees collected by the National Forest Biomass Modeling Program. 2) The basic wood density of Tilia is the arithmetic average value of two mean basic wood densities, one is 0.343 from 10 sample trees in reference [39] and another is 0.297 from the converted one-variable biomass model of Tilia amurensis. 3) The basic wood density of Cupressus is the weighted average value of two mean basic wood densities, one is 0.482 from 51 sample trees in reference [39] and another is 0.6400 from 138 sample trees collected by the National Forest Biomass Modeling Program. 4) The basic wood density of P. koraiensis is derived from the general model, a conversion of the one-variable aboveground biomass model of P. koraiensis in reference [40] at the point D=16 cm which is close to the mean diameter at breast height of all sample trees in references [24-36]. 5) F-J-P means Fraxinus mandshurica+Juglans mandshurica+Phellodendron amurense, and C-S-P means Cinnamomum+Sassafras+Phoebe. 6) The estimates of parameter a are all kept 4 decimal digits (3 or 4 significant digits). 7) The basic wood density values in references [24-36] have 4 decimal digits, and those in reference [39] have only 3 decimal digits. 8) “u” in this table means the number of sample trees unclear for Tilia and P. koraiensis.

To evaluate the applicability of aboveground biomass models in Table 1, the mensuration data of aboveground biomass of 14 tree species or genera were used to calculate relative errors (REs), and the results are listed in Table 2. It is showed that REs of models for 11 tree species are less than ± 10%, only the REs of models for Cryptomeria, Liquidambar formosana, and Robinia pseudoacacia exceed ± 10%, but less than ± 20%. By summarizing, the total RE for 14 tree species/ genera is -2.10%, no exceeding the common allowance ± 3%, and the average of absolute RE is 6.37%, less than the error allowance 10% [22]. Consequently, as for the biomass models of other 20 tree species or groups in Table 1, even though the predicted estimate for a special one may have uncertainty to some extent, but the predicted estimates for all the species should not exceed the error allowance, then the models are suitable for estimation of forest biomass at national level.

Species/genera RE/% Species/genera RE/%
Quercus -0.98 Populus -3.89
Abies -9.86 P. yunnanensis 1.26
Picea -7.41 Liquidambar formosana 19.72
Betula 4.06 P. tabulaeformis -2.32
Larix 1.25 Robinia pseudoacacia -12.78
Cunninghamia lanceolata -0.40 P. elliottii 4.29
P. massoniana -1.13 Cryptomeria 19.89

Table 2: Test results on applicability of the general one-variable aboveground biomass models for 14 tree species or genera.

Belowground biomass models

The mensuration data of biomass of 14 tree species or genera aforementioned were classified into two sets, coniferous and broadleaved. There are 2021 sample trees having both above- and belowground biomass data, where 1150 are coniferous and 871 are broadleaved. The compatible belowground biomass models and rootto- shoot ratio models for coniferous and broadleaved species were estimated respectively as eqn. (3), and the parameter estimates are listed in Table 3. It is showed that the estimate of second parameter b2 in root-to-shoot ratio model for coniferous species is close to 0, which is not significantly different from zero. That means the root-to-shoot ratio is close to a constant, almost having no relation to diameter of trees. Therefore, the average value 0.248 of root-to-shoot ratio can be used to estimate belowground biomass for coniferous species. The average value of root-to-shoot ratio for broadleaved species is 0.294, which is larger 18.5% than that of coniferous species. However, the root-to-shoot ratio for broadleaved species is significantly related to diameter of trees, thus it will be more accurate to estimate belowground biomass using the root-to-shoot ratio model.

Species a1 a2 b1 b2 c1 c2
Coniferous 0.14 2.3 0.25 -0 0.034 2.3
Broadleaved 0.13 2.4 0.47 -0.2 0.06 2.2

Table 3: Parameter estimates of compatible belowground biomass models for coniferous and broadleaved species

To evaluate the applicability of belowground biomass models and root-to-shoot ratio models in Table 3, the mensuration data of belowground biomass of 14 tree species or genera were used to calculate REs, and the results are listed in Table 4. It is showed that REs of models for 12 tree species are less than ± 20%, only the REs of models for P. yunnanensis and Cryptomeria exceed ± 20%. From analysis, the root-to-shoot ratios of P. yunnanensis and Cryptomeria are 0.160 and 0.348 respectively, which are just the minimum and maximum values among 9 coniferous species in Table 4. If considering the performance by coniferous and broadleaved species, the total REs are 4.81% and 0.15% respectively, no exceeding ± 5%; and the averages of absolute REs are 14.85% and 13.45%, less than the error allowance 15% for belowground biomass models [22]. Consequently, applying the models in Table 3 to estimate belowground biomass of other coniferous and broadleaved species except 14 tree species or genera aforementioned, even though the predicted estimate for a special one may have uncertainty to some extent, but the predicted estimates for all the species should not exceed the error allowance, then the models are suitable for estimation of forest biomass at national level.

Species/genera RE/% Species/genera RE/%
Quercus 2.09 Populus 18.69
Abies 11.60 P. yunnanensis 54.41
Picea 3.68 Liquidambar formosana -17.53
Betula -9.00 P. tabulaeformis -0.33
Larix -4.89 Robinia pseudoacacia -19.93
Cunninghamia lanceolata 7.38 P. elliottii -3.98
P. massoniana 18.60 Cryptomeria -28.77

Table 4: Test results of belowground biomass models for coniferous and broadleaved species.

Conclusion And Discussion

Based on the general biomass model M=0.3pD7/3 presented by Zeng and Tang and the published data of basic wood density for all tree species, one-variable aboveground biomass models for all 34-tree species or groups were developed. Additionally, using the mensuration data from the National Forest Biomass Modeling Program, the compatible belowground biomass models for coniferous and broadleaved species were established. According to the validation results for 14 tree species or genera, the one-variable biomass models developed in this paper can ensure the averages of absolute relative errors of above- and belowground biomass estimates less than the corresponding error allowances 10% and 15%, respectively. Thus, the developed biomass models can be used for forest biomass estimation at national level, which can be regarded as an important supplement to the ministerial standards on tree biomass models published in recent years.

Because the forest volume estimation in national forest inventory of China is based on one-variable volume tables/models, for forest biomass estimation we should use the compatible one-variable biomass models or biomass conversion factor models and root-to-shoot ratio models. The ministerial standards on tree biomass models recently published for 14 tree species or genera have laid a fine foundation for accurate estimation of nearly 70 percent forest biomass in China. The growing stocks of other 20 tree species or groups only occupy 30 percent of total growing stock. Before the ministerial standards on tree biomass models for these species have been published, the one-variable aboveground biomass models for various species and one-variable root-to-shoot ratio models for coniferous and broadleaved species developed in this paper could be used to estimate above- and belowground biomass. Considering that the sample trees of P. griffithii are too few, it is suggested to use the biomass model of P. densata instead of that of P. griffithii .

References

  1. Dixon RK, Trexler MC, Wisniewski J, Brown S, Houghton RA et al. (1994) Carbon pools and flux of global forest ecosystems. Science, 263: 185-190.
  2. Clark J, Murphy G (2011) Estimating forest biomass components with hemispherical photography for Douglas-fir stands in northwest Oregon. Canadian Journal of Forest Research, 41: 1060-1074.
  3. Clark J, Murphy G (2011) Estimating forest biomass components with hemispherical photography for Douglas-fir stands in northwest Oregon. Canadian Journal of Forest Research, 41: 1060-1074.
  4. Zeng WS, Zhang HR, Tang SZ (2011) Methodology on modeling of single-tree biomass equations. Beijing: Chinese Forestry Press.
  5. Zeng WS, Tang SZ, Huang GS, et al. (2010) Population classification and sample structure on modeling of single tree biomass equations for national biomass estimation in China. Forest Resources Management 3: 16-23.
  6. Zeng WS, Tang S Z (2010) Using measurement error modeling method to establish compatible single tree biomass equations system. Forest Research, 23: 797-803.
  7. Zeng WS, Tang SZ (2011) Establishment of belowground biomass equations for larch in northeastern and Masson pine in southern China. Journal of Beijing Forestry University 33: 1-6.
  8. Zhang LJ, Zeng WS, Tang SZ (2011) Comparison of nonlinear regression equation with intercept and segmented modeling approach for estimation of single tree biomass. Forest Research 24: 453-457.
  9. Zeng WS, Tang SZ (2011) Bias correction in logarithmic regression and comparison with weighted regression for nonlinear models. Nature Precedings.
  10. Fu LY, Zeng WS, Tang SZ (2011) Analysis the effect of region impacting on the biomass of domestic Masson pine using mixed model. Acta Ecologica Sinica, 31: 5797-5808.
  11. Zeng WS, Tang SZ (2011) Goodness evaluation and precision analysis of tree biomass equations. Scientia Silvae Sinicae 47: 106-113.
  12. Zeng WS, Tang SZ (2012) Modeling compatible single-tree aboveground biomass equations of Masson pine (Pinus massoniana) in southern China. Journal of Forestry Research 23: 593-598.
  13. Zeng WS, Zhang HR, Tang S Z (2011) Using the dummy variable model approach to construct compatible single-tree biomass equations at different scales—A case study for Masson pine (Pinus massoniana) in southern China. Canadian Journal of Forest Research 41: 1547-1554.
  14. Zeng WS, Tang SZ (2011) A new general allometric biomass model. Nature Precedings.
  15. Fu LY, Lei YC, Zeng WS (2014) Comparison of several compatible biomass models and estimation approaches. Scientia Silvae Sinicae, 50: 42-54.
  16. Zeng M, Nie XY, Zeng WS (2013) Compatible tree volume and aboveground biomass equations of Chinese fir in China. Scientia Silvae Sinicae 49: 74-79.
  17. Zeng WS (2015) Using nonlinear mixed model and dummy variable model approaches to construct origin-based single tree biomass equations. Trees-Structure and Function, 29: 275-283.
  18. Zou WT, Zeng WS, Zhang LJ, Zeng M (2015) Modeling crown biomass for four pine species in China. Forests, 6: 433-449.
  19. Zeng WS (2015) Integrated individual tree biomass simultaneous equations for two larch species in northeastern and northern China. Scandinavian Journal of Forest Research. 30: 594-604.
  20. Zeng WS, Zhang LJ, Chen XY, et al. 2017. Construction of compatible and additive individual-tree biomass models for Pinus tabulaeformis in China. Canadian Journal of Forest Research, 47: 467-475.
  21. Zeng WS, Duo HR, Lei XD, et al. 2017. Individual tree biomass and growth models sensitive to climate variables for Larix spp. in China. European Journal of Forest Research, 136: 233-249.
  22. State Forestry Administration (2015) Technical regulation on methodology for tree biomass modeling [LY/T 2258-2014]. Beijing: China Standard Press.
  23. State Forestry Administration (2015) Technical regulation on sample collections for tree biomass modeling [LY/T 2259-2014]. Beijing: China Standard Press.
  24. State Forestry Administration (2015) Tree biomass models and related parameters to carbon accounting for Pinus tabulaeformis [LY/T 2260-2014]. Beijing: China Standard Press.
  25. State Forestry Administration (2015) Tree biomass models and related parameters to carbon accounting for Pinus elliottii [LY/T 2261-2014]. Beijing: China Standard Press.
  26. State Forestry Administration (2015) Tree biomass models and related parameters to carbon accounting for Pinus yunnanensis [LY/T 2262-2014]. Beijing: China Standard Press.
  27. State Forestry Administration (2015) Tree biomass models and related parameters to carbon accounting for Pinus massoniana [LY/T 2263-2014]. Beijing: China Standard Press.
  28. State Forestry Administration (2015) Tree biomass models and related parameters to carbon accounting for Cunninghamia lanceolata [LY/T 2264-2014]. Beijing: China Standard Press.
  29. State Forestry Administration (2015) Tree biomass models and related parameters to carbon accounting for Larix [LY/T 2654-2016]. Beijing: China Standard Press.
  30. State Forestry Administration. 2017. Tree biomass models and related parameters to carbon accounting for Abies [LY/T 2656-2016]. Beijing: China Standard Press.
  31. State Forestry Administration (2017) Tree biomass models and related parameters to carbon accounting for Picea [LY/T 2655-2016]. Beijing: China Standard Press.
  32. State Forestry Administration (2017) Tree biomass models and related parameters to carbon accounting for Cryptomeria [LY/T 2657-2016]. Beijing: China Standard Press.
  33. State Forestry Administration (2017) Tree biomass models and related parameters to carbon accounting for Quercus [LY/T 2658-2016]. Beijing: China Standard Press.
  34. State Forestry Administration (2017) Tree biomass models and related parameters to carbon accounting for Betula [LY/T 2659-2016]. Beijing: China Standard Press.
  35. State Forestry Administration (2017) Tree biomass models and related parameters to carbon accounting for Liquidambar formosana [LY/T 2660-2016]. Beijing: China Standard Press.
  36. State Forestry Administration (2017) Tree biomass models and related parameters to carbon accounting for Robinia pseudoacacia [LY/T 2661-2016]. Beijing: China Standard Press.
  37. Fu LY, Zeng WS, Tang SZ (2017) Individual tree biomass models to estimate forest biomass for large spatial regions developed using four pine species in China. Forest Science, 63: 241-249.
  38. West GB, Brown JH, Enquist BJ (1997) A general model for the origin of allometric scaling laws in biology. Science 276:122-126.
  39. Institute of Wood Industry, Chinese Academy of Forestry (1982) The physical and mechanical properties of wood for major tree species in China. Beijing: Chinese Forestry Press.
  40. Chen CG, Zhu JF (1989) Handbook of tree biomass in northeastern China. Beijing: Chinese Forestry Press.
  41. Li HK, Lei YC (2010) Estimation and Evaluation of Forest Biomass and Carbon Storage in China. Beijing: Chinese Forestry Press.
Citation: Zeng WS (2018) Developing One-variable Individual Tree Biomass Models based on Wood Density for 34 Tree Species in China. Forest Res 7: 217.

Copyright: © 2018 Zeng WS. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Top