Journal of Tourism & Hospitality
Open Access
ISSN: 2167-0269
ISSN: 2167-0269
Research Article - (2017) Volume 6, Issue 3
Tourists’ get attracted towards India because of its diverse culture and geography. Apart from heritage and culture, the tourists from all over the world come here for various other purposes like medical, business, education and sports. The tourism industry of India is economically important and is growing rapidly. The tourism industry in India helps in the growth of other sectors like agriculture, small scale industries, self-employment, etc. This makes forecasting of tourists’ arrivals in India a prime focus of the government Forecasting is the process of making predictions of the future based on past and present data and analysis of trends. Tourism forecasting plays an important role in providing awareness and support for future development of the Indian tourism industry. In this paper, an attempt has been made to forecast tourists’ arrival using statistical time series modeling techniques with the help of secondary data.
<Keywords: Forecasting, Holt-Winter’s exponential smoothing model, ARIMA, Auto regression, Moving average
Modeling and forecasting tourists demand has received substantial attention among policy makers, hospitality management, researchers and other interest groups globally. Tourist’s footfalls immensely contribute towards the growth of economy’s Gross Domestic Product (GDP). It is one of the leading sources of foreign exchange earnings as well as generating employments opportunities. Despite the continued existence of number of antisocial activities and economic setbacks such as terrorism, naxal activities etc., India is still a wonderful and attractive destination for international tourists. Forecasting tourist arrival being a significant activity for its beneficiaries and stake holders’, several forecasting models have been applied to estimate and forecast the tourism demand globally. Large numbers of research papers have applied widespread time series models for forecasting tourism demand globally. Highly structured and an extensive survey of literature of earlier studies is provided by Crouch [1], Li et al. [2], Witt et al. [3].
On the other hand Song et al. [4] review the literature for post 2000 studies. This paper highlights few recent studies which applied time series model for forecasting tourism demand. The studies of Smeral et al. [5] applied ARIMA, SARIMA and naïve methods for forecasting tourism demand. The result reveals that advanced models like ARIMA or SARIMA model could not even outperform the simple Naïve model. Applying ARCH and GARCH model Chan et al. [6] tries to estimate and forecast volatility in tourism demand and its affect to various shocks. On the other hand, Turner et al. [7,8] have applied the structural equation modeling. Cho [9] concluded that artificial Neural Network (ANN) model outperform the exponential smoothing and ARIMA model in modeling and forecasting the tourism demand for Hong Kong.
While Wang [10] applied the fuzzy goal programming, Hernandez- Lopez [11] applied genetic algorithms for forecasting tourism demand. Huarng [12] used fuzzy time series models for forecasting tourism demand in Tiwan. Concha [13] presented a paper for forecasting tourism inflows in Spain using ARIMA and Google index relating search made in the country.
The main objective of the study is to forecast tourists’ arrival in India using statistical time series modeling techniques- Holt Winters method and ARIMA modeling. Further comparative analysis of the both the methods is done on the basis of certain performance metrics.
The annual tourists’ arrival in India (in thousands) for the period 1981-2014 is collected from India Tourism Statistics, Ministry of Tourism, and Government of India. The tests are conducted for 30 years that is from 1981-2010 and prediction period is from 2011- 2014. Holt Winter’s Exponential Smoothing and ARIMA models are statistical tools used for forecasting of the number of tourists’ arrival in India from 2011-2014.
Holt winters exponential smoothing (HWES)
Exponential smoothing modelings are simple, fast and inexpensive. They are used frequently throughout the world. Exponential smoothing methods are a class of methods that produce forecasts with simple formulae, taking into account trend and seasonal effects of the data. These procedures are widely used as forecasting techniques in inventory management and sales forecasting. Ord et al. [14] had put exponential smoothing procedures on sound theoretical ground by identifying and examining the underlying statistical models.
The HWES method estimates three smoothing parameters, associated with level, trend and seasonal factors. The seasonal variation can be of either an additive or multiplicative form. The multiplicative version is used more widely and on average works better than the additive [15]. If a data series contains some values equal to zero, the multiplicative method may not be used. In such cases additive Holt- Winters forecasting model is used [16,17]. A problem which affects all exponential smoothing methods is the selection of smoothing parameters and initial values, so that forecast is better in accord with time series data. The parameters of smoothing (and initial) in HWES are estimated by minimizing the mean square error (MSE). The Holt Winters’ Exponential Smoothing Model is given in equations (1)
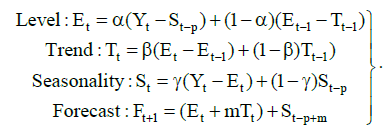 (1)
(1)
Where α, β, γ are smoothing constants and are chosen so that MSE is minimized.
Auto regressive integrated moving average models (ARIMA)
Univariate ARIMA models use only the information contained in the series itself. Thus, models are constructed as linear functions of past values of the series and/or previous random shocks (or errors). Forecasts are generated under the assumption that the past history could be translated into predictions for the future. The ARIMA model uses the fact that arrival of tourist’s is a stochastic time series. This modeling regresses the dependent variable Yt on p-lags of the dependent variable (Autoregressive) and q lags of the error term (Moving Average). Sometimes instead of dependent variable Yt, LdYt can be used as the dependent variable. Here L is the one step lag operator, i.e., LYt=Yt-1. The general equation of ARIMA model [2] is as follows:
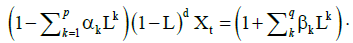 (2)
(2)
Where εt is white noise error? It is identically and independently distributed with mean zero and common variance σ2 across all observations. In ARIMA model following steps are followed:
Step1: Model identification: According to Box and Jenkins [18,19] two graphical procedures are used to access the correlation between the observations within a single time series data. These devices are called an estimated autocorrelation functions and the estimated partial autocorrelation function. These two procedures measure statistical relationships within the time series data. Next step for identification is summarization of statistical correlation within the time series data. One has to choose the appropriate ARIMA model from the whole family of ARIMA as suggested by Box and Jenkins. The autocorrelation function (ACF) and partial autocorrelation functions (PACF) of a series together are the most powerful tool, usually applied to reveal the correct values of the parameters. The ACF gives the autocorrelations calculated at lags 1, 2 and so on, while PACF gives the corresponding partial autocorrelations, controlling the autocorrelations at intervening lags. Every ARIMA model have their unique ACF and PACF associated with it. One has to select the model whose theoretical ACF and PACF resembles the anticipated ACF and PACF of the time series data [1].
Step 2: Parameter estimation: Maximum Likelihood Estimation Method (MLE) or Modified Least Squares Method (MLS), whichever suitable for the time series data is used to estimate the coefficients of the model. The final results includes the parameter estimates, standard errors, estimates of residual variance, standard error of the estimate, natural log likelihood, Akaike’s Information Criterion (AIC). Model selection is based on the minimization of AIC. To identify the optimal ARIMA model, different combinations of AR and MA are tested. The one for which AIC have minimum values are considered to be optimal model. AIC is given by:
AIC=-2logL+2m (3)
m=p+q and L is likelihood function (3).
Step 3: Diagnostic checking: Diagnostic checks help to determine if the anticipated model is adequate. In this step, an examination of the residuals from the fitted model is done and if it fails the diagnostic tests, it is rejected and one have to repeat the cycle until appropriate models is achieved.
Step 4: Forecast: These models are regression models that use lagged values of the dependent variables and/or random distributing term as explanatory models. These models rely heavily on the auto correlation pattern in the data. This model regresses the dependent variable on p lags of the dependent variable (Auto Regressive) and q lags of the error term (Moving Average).
Performance evaluation: To evaluate the performance of the various models the Root Mean Square Error (RMSE) and the Mean Absolute Percentage Error (MAPE) are used, which are as follows:
 (4)
(4)
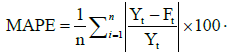 (5)
(5)
Where Yt is the observed value and Ft is the forecast value and n is the number of time period used as forecasting.
The main aim of the paper is to predict number of tourists’ arrival in India and compare the two forecasting models. Table 1, shows the annual tourists’ arrival in India for period 1981-2012. The time plot is shown in Figure 1.
| S.No | Year | (Observed) Foreign Tourist Arrived (Millions) | S.No | Year | (Observed) Foreign Tourist Arrived (Millions) |
|---|---|---|---|---|---|
| 1 | 1981 | 1.28 | 18 | 1998 | 2.36 |
| 2 | 1982 | 1.29 | 19 | 1999 | 2.48 |
| 3 | 1983 | 1.3 | 20 | 2000 | 2.65 |
| 4 | 1984 | 1.19 | 21 | 2001 | 2.54 |
| 5 | 1985 | 1.26 | 22 | 2002 | 2.38 |
| 6 | 1986 | 1.45 | 23 | 2003 | 2.73 |
| 7 | 1987 | 1.48 | 24 | 2004 | 3.46 |
| 8 | 1988 | 1.59 | 25 | 2005 | 3.92 |
| 9 | 1989 | 1.74 | 26 | 2006 | 4.45 |
| 10 | 1990 | 1.71 | 27 | 2007 | 5.08 |
| 11 | 1991 | 1.68 | 28 | 2008 | 5.28 |
| 12 | 1992 | 1.87 | 29 | 2009 | 5.17 |
| 13 | 1993 | 1.76 | 30 | 2010 | 5.78 |
| 14 | 1994 | 1.89 | 31 | 2011 | 6.31 |
| 15 | 1995 | 2.12 | 32 | 2012 | 6.58 |
| 16 | 1996 | 2.29 | 33 | 2013 | 6.97 |
| 17 | 1997 | 2.37 | 34 | 2014 | 7.68 |
Table 1: Foreign Tourists Arrival in India from 1981-2014.
Holt-winter’s exponential smoothing (HWES)
HWES model is appropriate when trend and seasonality are present in the time series. It decomposes the series down into three components that are base, trend and seasonal components. Additive model of Holt-Winter’s Exponential Smoothing is used for forecasting. In defining the smoothing parameters of base, trend and seasonality statistical program Solver, a tool contained in Excel is used. For HWES model the best fitted value of �� and �� are 0.4 and 0.3 respectively. MAPE (1.56) and RMSE (0.22) are least. Finally the observed and forecasted values are shown in Table 2 and Figure 2.
| S.No | Year | Foreign TouristsArrival (Millions) | |
|---|---|---|---|
| Observed Values | Forecasted Values (HWES) | ||
| 1 | 2011 | 6.31 | 6.19 |
| 2 | 2012 | 6.58 | 6.59 |
| 3 | 2013 | 6.97 | 6.97 |
| 4 | 2014 | 7.68 | 7.36 |
Table 2: Forecast of Annual Foreign Tourist Arrival in India from 2011-2014 using HWES.
Auto regressive integrated moving average (ARIMA)
ARIMA uses the fact that foreign tourists’ arrival is a stochastic time series. In this paper ARIMA modelling is done using R-programming from Figure 1, it is observed that the given time series is non-stationary, on applying Dickey-Fuller [20] test also tourists’ arrival series d(0) for lag order (2) is found to be non-stationary. Therefore, the series has to be transformed to a stationary series, by differencing. According to Dickey Filler test, the third difference series d (3) for lag order (2) is found to be stationary. Also from Figure 2, it is clear that the third difference series is stationary (Figures 3-5).
It is observed from the Figure 3, ACF has significant spike at lag 0, 2, 5, indicates MA(0), MA(2), MA(5) term and also there is significant spikes at lag 2 in PACF shown in Figure 4, indicates AR(2) term. After trying various combinations of pandq considering significant spike in both ACF and PACF. The AIC (6.96) is least for ARIMA (2, 3, 5) model. Diagnostic check has be done on this model using Box-Ljung test. It is found that the ARIMA (2, 3, 5) model is fit for forecasting foreign tourists’ arrival in India (Figure 5).
Using ARIMA (2, 3, 5) model the forecasted values of foreign tourists’ arrival in India has been obtained which are shown in Table 3. The performance evaluation measures for this ARIMA model are MAPE (1.38) and RMSE (0.18).
Table 3 shows that annual forecasted values of foreign tourists’ arrival in India 2011-2014 using ARIMA (2, 3, 5) are significantly similar to the observed values.
| S.No | Year | Foreign Tourists Arrival in India (Millions) | |
|---|---|---|---|
| Observed Values | Forecasted Values ARIMA (2,3,5) | ||
| 1 | 2011 | 6.31 | 6.41 |
| 2 | 2012 | 6.58 | 6.68 |
| 3 | 2013 | 6.97 | 7.13 |
| 4 | 2014 | 7.68 | 7.67 |
Table 3: Forecast of Annual Foreign Tourist Arrival in India from 2011-2014 using ARIMA (2, 3, 5).
Table 4 shows comparison annual forecasted values of foreign tourists’ arrival in India 2011-2014 using HWES and ARIMA (2, 3, 5) and both of them are significantly similar to the observed values
| S.No | Year | Foreign Tourists Arrival in India (Millions) | ||
|---|---|---|---|---|
| ObservedValues | Forecasted Values (HWES) | Forecasted Values ARIMA (2,3,5) | ||
| 1 | 2011 | 6.31 | 6.19 | 6.41 |
| 2 | 2012 | 6.58 | 6.59 | 6.68 |
| 3 | 2013 | 6.97 | 6.97 | 7.13 |
| 4 | 2014 | 7.68 | 7.36 | 7.67 |
| MAPE | 1.56 | 1.38 | ||
| RMSE | 0.22 | 0.18 | ||
Table 4: Comparison of Observed and Forecasted values of Annual Foreign Tourists’ Arrival in India from 2011-2014 using HWES and ARIMA (2, 3, 5).
The study aimed at forecasting foreign tourists’ arrival in India and to compare HWES and ARIMA based on MAPE and RMSE. Holt Winter’s Exponential Smoothing Model and ARIMA (2, 3, 5) model both are quiet efficient for forecasting foreign tourists’ arrival in India. On the basis of results obtained and the past data used, ARIMA (2, 3, 5) model is better than Holt Winter’s Exponential Smoothing. Therefore ARIMA model is found to be the best fit model for foreign tourists’ arrival in India.