Mathematica Eterna
Open Access

Short Communication on Introduction of Graph Theory

Domson N^{* *}Correspondence: Domson N, Associate Professor, Emeritus-Ankara University, Turkey, Email:

Author info »

Graph theory is rapidly getting into the mainstream of mathematics mainly due to its applications in diverse fields which include biochemistry (genomics), EE (communications networks and coding theory), engineering (algorithms and computations) and research (scheduling). The wide scope of those and other applications has been well-documented cf. The powerful combinatorial methods found in graph theory have also been wont to prove significant and well-known ends up in a range of areas in mathematics itself. the most effective known of those methods are associated with part of graph theory called matchings, and therefore the results from this area are accustomed prove Dilworth's chain decomposition theorem for finite partially ordered sets. An application of matching in graph theory shows that there's a typical set of left and right coset representatives of a subgroup during a finite group. This result played a vital role in Dharwadker's 2000 proof of the fourcolor theorem. The existence of matchings in certain infinite bipartite graphs played a crucial role in Laczkovich's affirmative answer to Tarski's 1925 problem of whether a circle is piecewise congruent to a square. The proof of the existence of a subset of the 000 numbers R that's non-measurable within the Lebesgue sense is because of Thomas [21]. Surprisingly, this theorem are often proved using only discrete mathematics (bipartite graphs). There are many such samples of applications of graph theory to other parts of mathematics, but they continue to be scattered within the literature [3][16]. during this paper, we present some selected applications of graph theory to other parts of mathematics and to numerous other fields normally.

In a college there are m professors x1, x2, ..., xm and n subjects y1, y2, ..., yn to be taught. providing professor xi is required (and able) to show subject yj for pij periods (p = [ pij ] is termed the teaching requirement matrix), the school administration wishes to form a timetable using the minimum possible number of periods. this can be referred to as the timetabling problem [4] and might be solved using the subsequent strategy. Construct a bipartite multigraph G with vertices x1, x2, ..., xm, y1, y2, ..., yn specified vertices xi and yj are connected by pij edges. We presume that in anyone period each professor can teach at the most one subject which each subject is taught by at the most one professor. Consider, first, one period. The timetable for this single period corresponds to an identical within the graph and, conversely, each matching corresponds to a possible assignment of professors to subjects taught during this era. Thus, the answer to the timetabling problem consists of partitioning the sides of G into the minimum number of matchings. Equivalently, we must properly color the sides of G with the minimum number of colours. We shall show yet one more way of solving the matter using the vertex coloring algorithm [7]. Recall that the road graph L(G) of G has as vertices the perimeters of G and two vertices in L(G) are connected by a foothold if and providing the corresponding edges in G have a vertex in common. the road graph L(G) may be a simple graph and a correct vertex coloring of L(G) yields a correct edge coloring of G using the identical number of colours. Thus, to resolve the timetabling problem, it suffices to seek out a minimum proper vertex coloring of L(G) using. We demonstrate the answer with atiny low example. The teaching requirement matrix p = [ pij ] is given below in Figure 1.

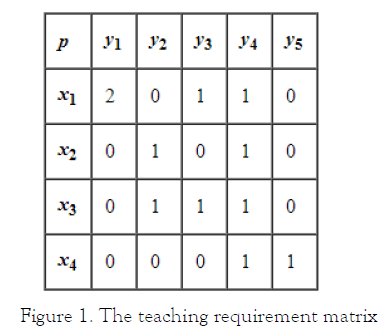
Figure 1. The teaching requirement matrix