Mathematica Eterna
Open Access

Probability Distributions of Phases I

Jan Brosius^* and Walter Brosius ^*Correspondence: Jan Brosius, Department of Theoretical Chemistry, University of Valencia, Valencia, Spain, Email:

Author info »

Introduction

In a short review was given of the old probabilistic DM (Direct Methods) way for calculating phase distributions [1].

There were two mathematical approaches see (A) and (B) below (A): The basic R.V.’s (Random Variables) are the set of the 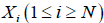that are distributed independently and uniformly over the asymmetric unit (we consider in this paper only P1) and one studies the normalized structure factors 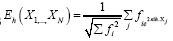And one calculates the probabilities of the phases 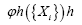(B): The basic R.V.’s are the reciprocal vectors h that are distributed uniformly and independently over reciprocal space and one keeps the X_iconstant. This method can give algebraic equations as follows: One can study the structure factors 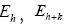and we consider only h as the basic reciprocal vector and one keeps k fixed. The B₃,0 formula is an equation obtained this way. Although this equation gives the value of 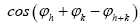in theory, in practice this equation is wrong for high N, which is due to accidental overlap of the xi which invalidates the calculation of the joint probabilities of 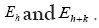Even when one calculates the joint probabilities 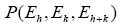where h and k are the basic R.V.’s one must assume no accidental overlap of the xi (which becomes a problem for high N.). The calculation of joint probabilities gives then the same results as in (A) above.

(C): Using method (A) one can derive the probability of the cosine invariant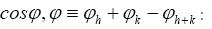

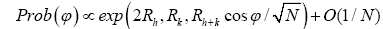
It follows that this formula

Loses predictive power for high N.

Cannot predict negative cosines.

The probabilities of quartets, quintets, etc. are even worse since they are of order of 1/N (for quartets), of order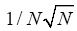 (for quintets), etc. (Although one can get a quartet formula that theoretically predicts negative cosines for the quartet (but again with too low predictive power)). At the end of the twentieth century nobody was busy anymore with calculating prob-abilistic phase distributions using one of the methods (A) or (B). For the calculations of structures with high N (N being here the number of independent non-H atoms in the asymmetric unit), one began to devise methods in direct space to solve crystal structures. One uses an automatic cyclical process: (a): Phase refinement (for instance with the use of the (modified) tangent formula) in reciprocal space and; (b): With the imposition in real space of physically meaningful constraints through an atomic interpretation of the electron density, with minimization of a well-chosen FOM (Figure Of Merit) of the phases. One of these methods in DM is known as the SnB (Shake and Bake) algorithm with N 1200 [2,3]; Another is the twin variables approach with 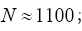Sir2000 the successor of SIR97 and SIR99 although different from SnB: (e.g. triplet invariants via the P10 formula with 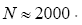Another interesting result is the solution of a crystal when a substructure is known where N may become higher [4-9]. For an overview of DM before the year 2000 we refer to Giacovazzo [10].

(D): In order to circumvent these problems one approach might be to consider R.V.’s (x_i)that are no longer independent neither uniformly distributed, say a dependence through a positive distribution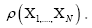

One can give such distributions by using the functions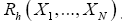

But then one encounters insurmountable mathematical difficulties.

The solution is to not consider the x_i as R.V.’s anymore but to replace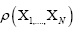 by a field 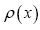and to sample the field over the allowable function space. What we shall discuss here is a novel way for doing DM (Direct Methods).

(E): Differences with our approach

• We shall be able to solve any structure (any N) ab initio.

• Much lower CPU time.

• Let then with our approach we can easily calculate the probability distribution of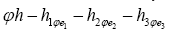 for any h. No need to compute all possible triplets.

• Easy to incorporate any given substructure.

• Easy to calculate the PD’s (Probability Distributions) of phases: One only needs to take derivatives.

In this paper we shall give the mathematical basis that is necessary for this completely new DM approach. This approach is not mathematically as simple as in (A) and (B) but it is perfectly doable. It consists in using the atomic distribution function (x) as the basic random variable. The method will also be based on a functional integration over the random variable and using a nonstandard fuzzy approach wherein Dirac delta functions (among which a novel delta function representation for angle variables) are replaced by nonstandard fuzzy delta functions. To show the strength of the method, a simple formula was given in Brosius for the distribution of the triplet phase formula of the form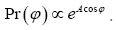

Where A is a function depending (not on N!) on the structure factors of the first neighborhood of the triplet [1].

In this paper a more profound mathematical foundation of our DM approach is given and this will be a major improvement compared to Brosius [1]. Recall that the sampling is done over positive functions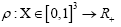 (in the space group P1) and that the R.V.’s that we study are the phases 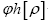which are defined by the relation 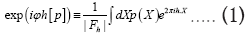Where is a R.V. defined by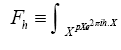

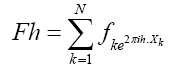
and from now on we shall use the notations

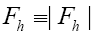
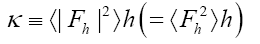
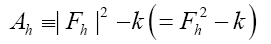
One then needs to define a probability density 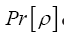on the sample space ρ's We build up 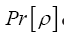by fuzzy Dirac delta functions in 4 steps

Through constraints of the form 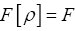by using fuzzy Dirac delta’s 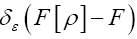(ε_a positive infinitesimal).

Next through maximization: Adding obvious terms to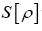 where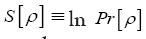 that cannot be added by using a constraint, like e.g. the term.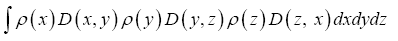

Eventually we add fermionic terms to z, like e.g.

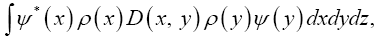
By imposing the mathematical requirement on the basic R.V. ρ that the different atoms in the unit cell of the crystal repel each other.

The idea is that if one would consider a function 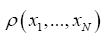for which it is known that 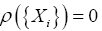whenever x_i equals some x_j, this can be done by requiring that 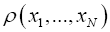is antisymmetric antisymmetric x_i, that is

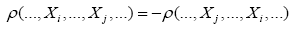
Inspired by modern QFT (Quantum Field Theory) we replace 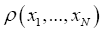by an antisymmetric (fermionic) field 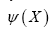with the property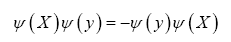

giving thus

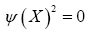
The added benefit is then that the different x_i will repel each other. Now one has two basic R.V.’s: ρ and ψ and we must integrate over ρ and ψ.

One can also sample over the set of Gaussian (normal) distributions by using the substitution

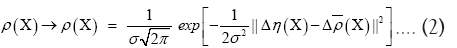
where 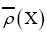represents the true electronic distribution and 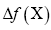is the laplacian of f at the point x.

As in QFT, D (x, y) is called the propagator from the point y to x. Using constraints we shall see that the first candidate for D (x,y) is Q(x–y) where Q is the origin-removed Patterson function defined here by

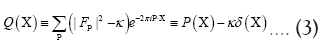
This propagator depends on N since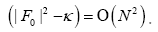

Notations and formulas

The error function [11,12].

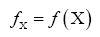
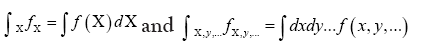
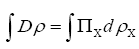
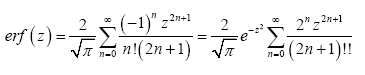
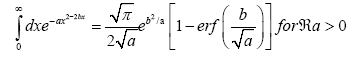
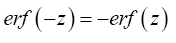
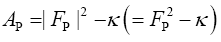
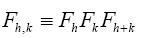
A without subscript stands for some infinite positive number.

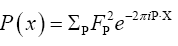
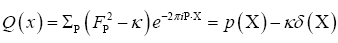
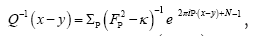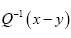where is the inverse of the kernel operator Q(x–y)

The phase random variable 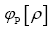is defined by 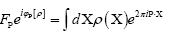where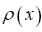 denotes the atomic distribution and the function ρ is our basic R.V.

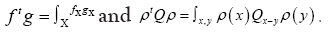
The functional integral

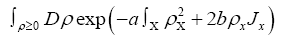
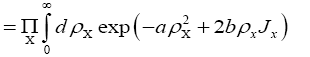
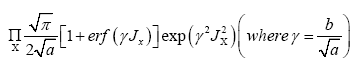
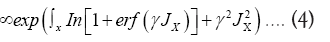
The constants. We define the constants by the series

The bn;m constants, defined by

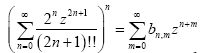
Our representation of 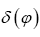for an angle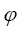is

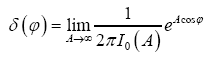
We then define the fuzzy nonstandard 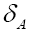function by

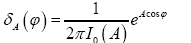
For real x (not an angle) we define the nonstandard fuzz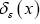y by

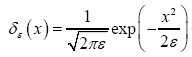for positive infinitesimal ε, and for complex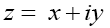

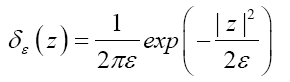
For some set H of reciprocal vectors we define

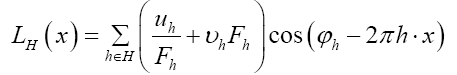
and sometimes we simply write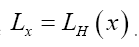

We use the explicit definition of the functional derivative by

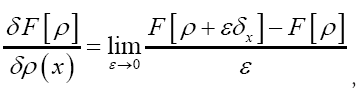
Where

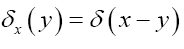
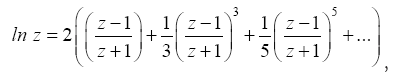
where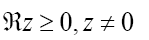

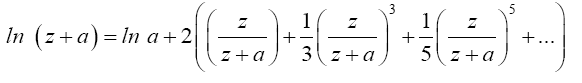; Where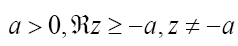

Some vector calculus: (f, g: vector valued functions, h a scalar function)

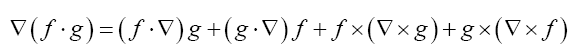
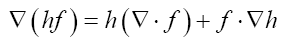
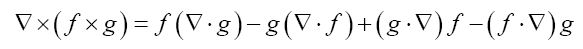
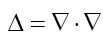
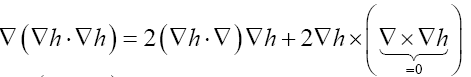
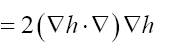
Recall that in three dimensions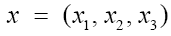

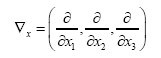
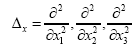
Preliminary knowledge

For an introduction on nonstandard theory we refer to Diener et al. and for a more advanced text see Nelson [13,14].

Nonstandard theory: Standard numbers are the known numbers: 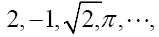the other numbers are the nonstandard real numbers which make up the field R. It is important to observe that there are an infinity of infinite numbers in R that are greater than any standard real number. Also there are an infinity of infinitesimals ε in R for which the absolute value |ε| is less than any positive standard number in R. From the axioms it follows that for every positive infinitesimal 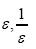is a positive infinite number and vice versa. Note that an infinite number is different from 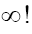In this paper we use A to denote an infinite positive number and ε will always denote (unless explicitly noted otherwise) a positive infinitesimal 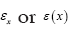will denote a function that associates a positive infinitesimal with every position x in the unit cell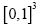 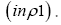We will use this function in our fuzzy Dirac delta. 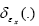We shall use the notation when we deal with angle variables.

Anticommuting variables: In a detailed exposition of anticommuting numbers is given [1]. In this subsection we shall only expose the bare minimum needed to read this paper. For more information, we refer to Weinberg, Siegel, Kuzenko et al. and for a more mathematical treatment to Bruhat et al. and deWitt [15-19].

One starts with a set of anticommuting numbers θ_λ:

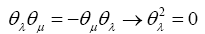
From this follows that every even product of such anticommuting numbers is commuting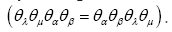 Also one adds the axiom: 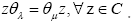Then the algebra 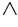is defined as the set of all finite sums of products.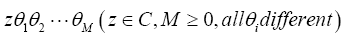

When M is even, this is a commuting number (also called even) and when it is odd it is an anticommuting number (also called odd). Sums of such products with even M do commute and are called even, and with odd M these sums are anticommuting and are called odd. Every z∈C is also even. It follows that every 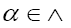is a sum 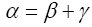with β even and γ odd.

An involution defined such that, 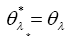and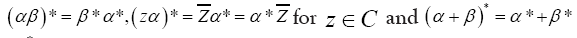 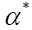is odd when 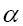is odd and even when otherwise. One calls 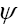is odd when α is odd and even when otherwise. One calls ψ or ψ_x an odd function of x if ψ_x is odd for every x. It then follows that 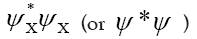is even. Then the derivative 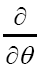with respect to the anticommuting variable θ is defined by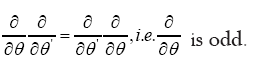

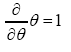
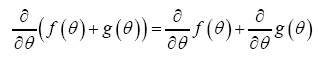
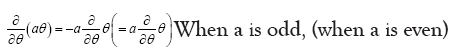
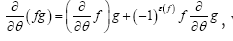where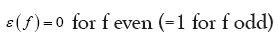

A function 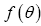of an odd variable θ has the simple form 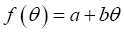(Taylor expansion), (here a is odd when f is odd, and even otherwise, but b has the opposite statistics of f). This can be generalized for a function 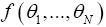of N anti-commuting variables: The coefficients of even products in the expansion of the θ_i have the same statistics as f, whereas the coefficients of uneven products have the opposite statistics. Next one defines the integration 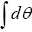as

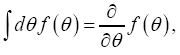
and the multiple integration

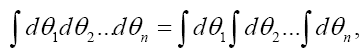
It is also convenient to define θ as an odd element:

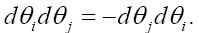
Also the following formulas are important

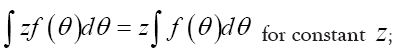
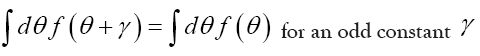
Note that the set of all odd numbers has vanishing volume

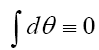and

Discussion

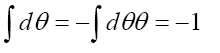
The four determinants are listed below. The following Theoremes are:

Theorem 1: Let M be an matrix n×n– matrix. Then

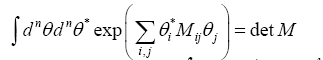
where by definition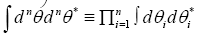

Proof develop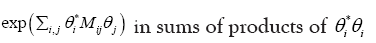

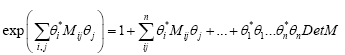
Since,

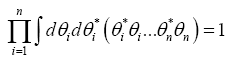the theorem follows.

The continuous version is as follows. Let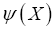 be an anticommuting variable for every X in the unit cell. Then,

where one has defined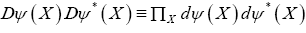

Theorem 2: Suppose now that the inverse M^–1 exists and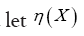 be an anticommuting variable for every X. Then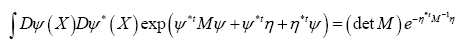

Where

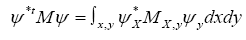
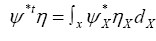
Proof let

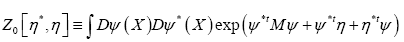
Then transform

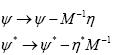
and substitute this in 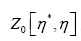Then using the relation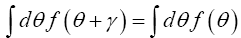

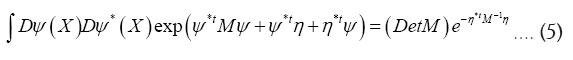
Thus

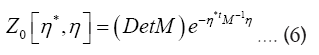
Also

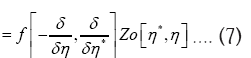
The minus sign arises from the observation that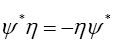 in

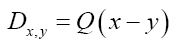
Indeed, note that

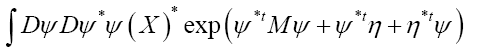
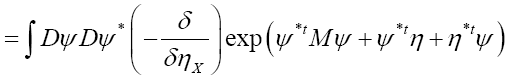
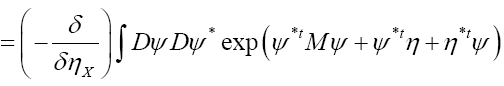
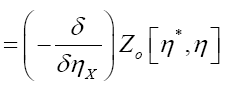
The probability functional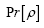

We shall show that we can obtain the following probability function 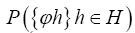(H is some set of reciprocal vectors) given by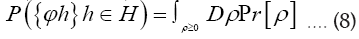

where 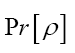is given, up to a phase unimportant constant, by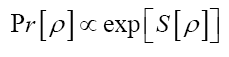

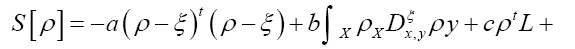
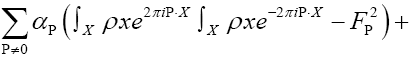
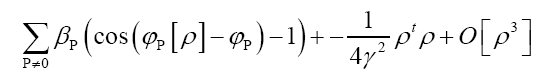
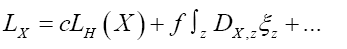
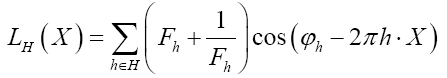
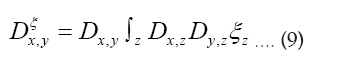
where 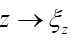denotes chemical information or an intermediate iteration of ρ.

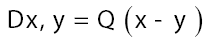
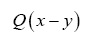will be the basic operator for all our 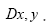First we need the following theorem:

Theorem 3: Let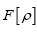 be a functional of 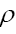such that 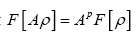where A is a positive infinite number and p an integer ≥1. If we impose the constraint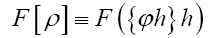

where F has the property that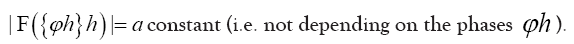

Then if we define the action functional 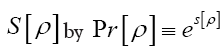(where c>0 is a constant) Then 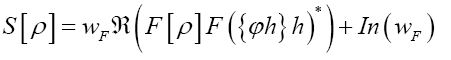(where w_F>…. (10)

For a sequence of such 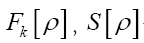will become (if we drop the constant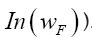

Proof we impose this constraint by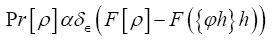

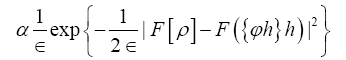
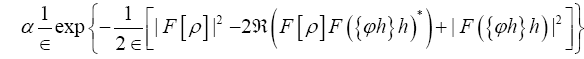
Since 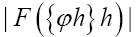is independent of the ϕ,h one can drop it in the above exponent. Next change 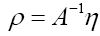and choos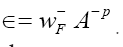e Since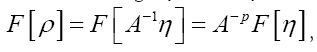 one obtains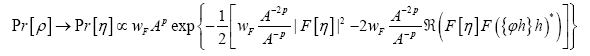

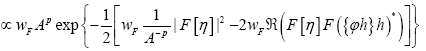
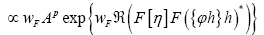
since 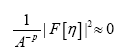(infinitesimal). Also under the change 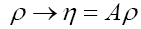integral volume 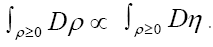So finally ( after replacing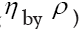

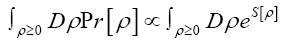
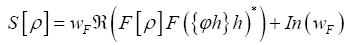
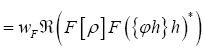(if we drop the constant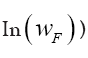

Theorem 4:One can write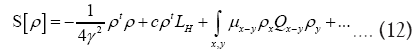

Where

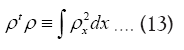
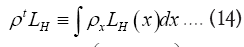
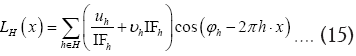
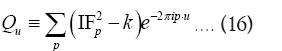
where from now on 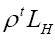is included 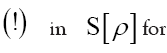convenience, with parameters

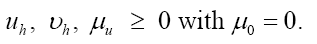
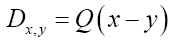
Proof.

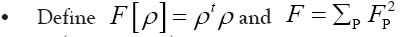and use the Dirac Then

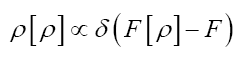
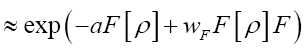
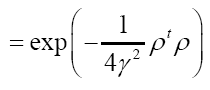
where we defined 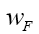such that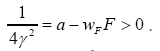

• The R.V. 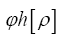was defined by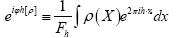

Then the probability distribution of 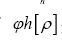is generated by the expression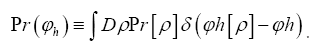

But, (when A is infinite and positive)

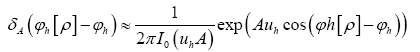
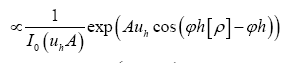
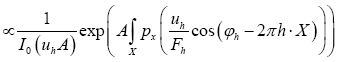
After the transformation 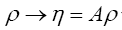obtain the result

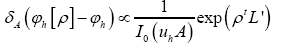
where 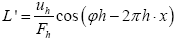For convenience, from now on, we shall include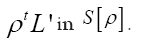

• Next use 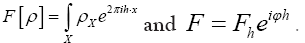Then

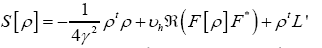
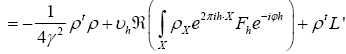
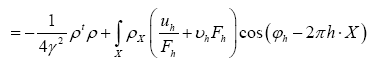
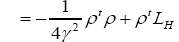
where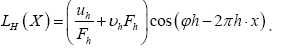

• For every 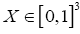we impose the constraint

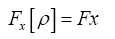
where

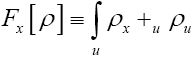
and

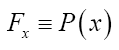
Then, according to theorem 1 above, one has

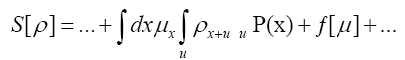
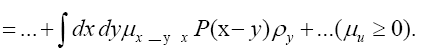
Next note that there is a phase unimportant peak 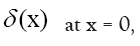and define Q by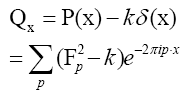

Then if one chooses the positive function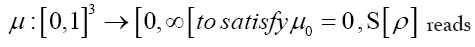

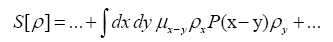
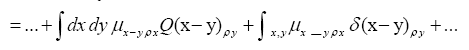
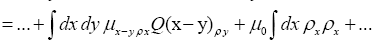
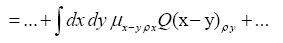
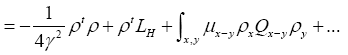
One can also add other terms to 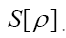For example consider the triplet expression

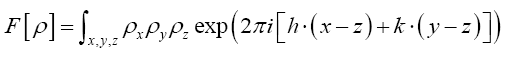
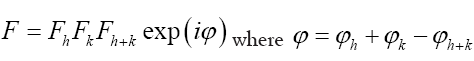
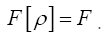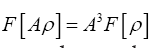Impose now the constraint Since and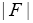 is constant in the phases we can write according to the basic theorem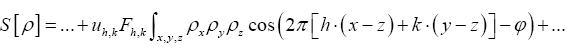

where 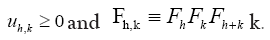One can also do the same for quartets, quintets and so on. Next impose for the triplet, the constraint.

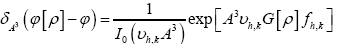
where

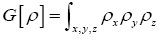
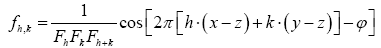
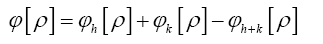
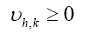
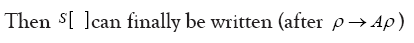
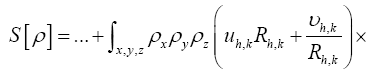
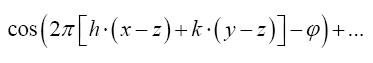
Note that Important, 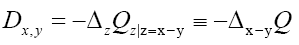from now on we shall treat all weights 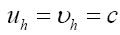the same: We shall not distinguish between the different measurements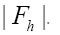

The same will be true for 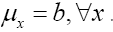The same is true for the 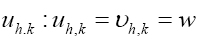But we shall not consider triplet terms of order 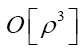in this paper. So now we have arrived at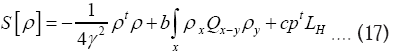

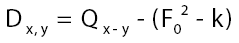
This propagator Dx,y does not depend anymore on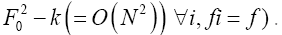 In the sequel we shall simply say: “does not depend anymore on N”. It is better than 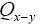Indeed to see this we can write 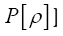as

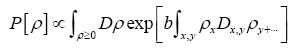
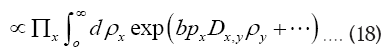
This last expression becomes very low whenever x-y is not an interatomic vector since then 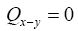and thus 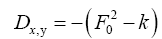and thus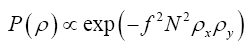

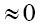
That is 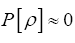demoting such a ρ. We recall that we have also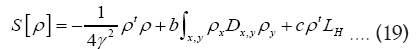

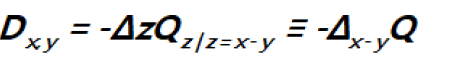
Recall that 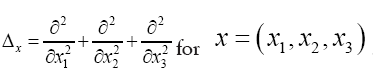In order to see what this new propagator can offer let us look at Q_x.

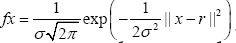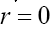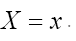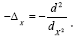Q_x is an N-sum of gaussian functions. Let us consider one of them, say For sake of convenience we take now and we consider the one dimensional case ThenAnd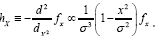 Thus at x=0 we see that 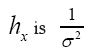times larger than 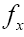since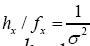 which is very large since σ is very small. The function 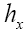then drops very fast to zero at 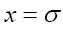after which it remains negative, attains a negative minimum and then goes fast to 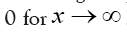Also there is exactly one large negative minimum in the range Exactly as discussed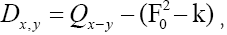 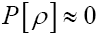for a ρ for which 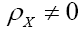at one of these minima. For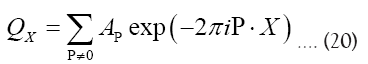

we get 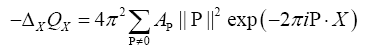Because of the differentiation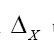this 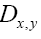does not depend on N

Note, 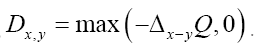This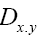 can also be used; Then there are no negative minima, but in order to make it N independent, one has to follow the procedure used in 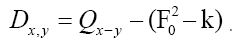That is we must subtract the term 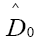in the Fourier expansion of 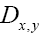to get a new propagator that is N-independent: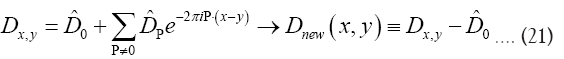

Improvements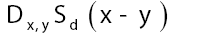

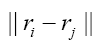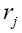Let d be the maximum distance of all where is the nearest neighbour of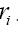Then we can obviously replace the 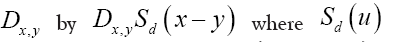is the characteristic function of the sphere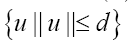in the asymmetric unit of the crystal. Thus 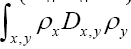becomes 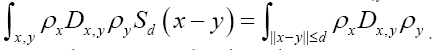If we know d we can then improve the phase densi- ties 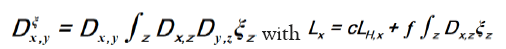When ξ is a given chemical information (be it a submodel or an intermediate state ofduring iteration) then we can derive a new propagator, with notation 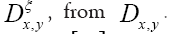Indeed if we look at the term 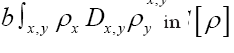it is clear that we can consider an (improved) term 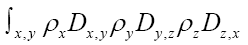and replace 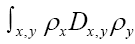with the latter term. For instance if 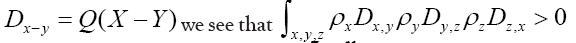when 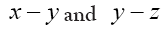and and 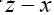are interatomic vectors; This is a stronger restriction on than merely the condition 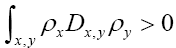Now if 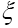is a submodel of then we can also replace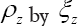

and obtain again a term of order 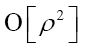by replacing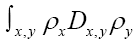by the stronger condition (on ρ ) 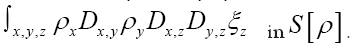But now also 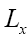changes to 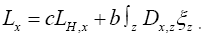Indeed, in 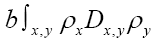we can replace 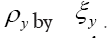Then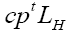 becomes 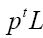where now (Remark that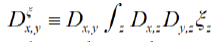is symmetric whenever 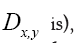and we replace b by another parameter f. Hence for a given submodel ξ we can now write a better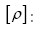

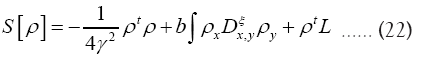
with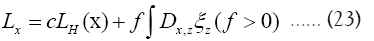

Example: We can always place the origin of the asymmetric unit wherever we want, i.e. we can always suppose that one atomic vector, say a, is given. This means that at least we can always use the chemical information. 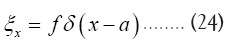Then we get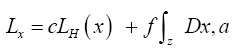

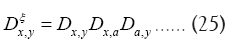
Now we can show that with this we can directly calculate the density of the phase invariant.

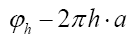instead of simply 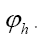Indeed consider the functional (where we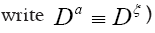

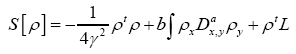
Next we do the functional change of variables: 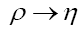where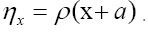 Then the Jacobian is the inverse of the determinant of the matrix 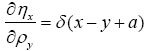which is not dependent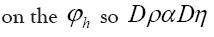Then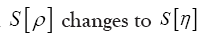

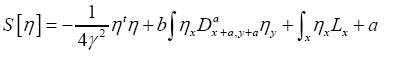
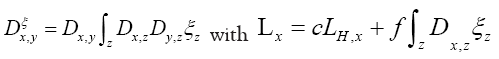
and 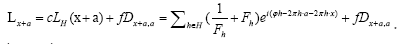Defining the phase invariant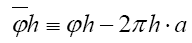

and considering the case that interests us most 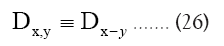we can write now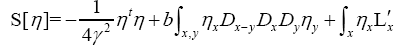

Where now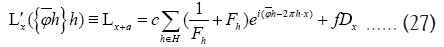

Remark: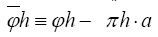 is indeed a phase invariant because under a translation of the origin 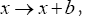also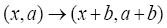 and thus 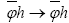under this translation which shows that 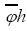is indeed a phase invariant. For the reciprocal vectors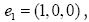 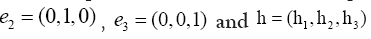we can writ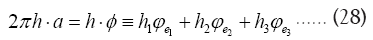e where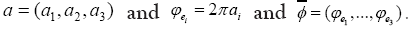 So we can write the phase invariant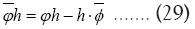

The case for general ξ: Let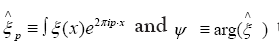 then 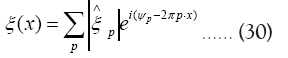and consider 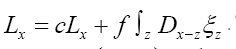Then we apply the same functional change 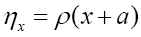and we then get for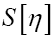

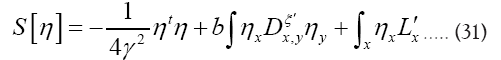
where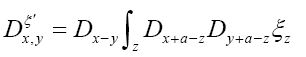

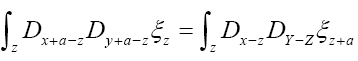
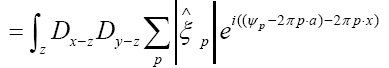
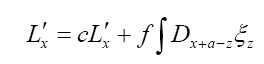
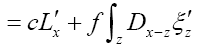
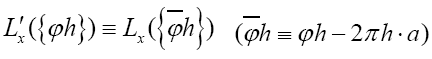
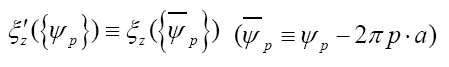
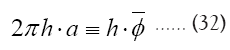
Note: From now on we shall always write 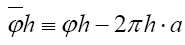instead of 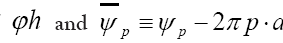instead of 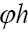resp.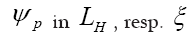

A fermionic action functional and a new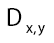

One knows that the different atoms in the unit cell repel each other. So, our random variable ρ should be chosen in such a way that the different peaks of ρ(x) spread over the unit cell and repel each other. This can be treated by considering ρ as an antisymmetric (fermionic) field written now as ψ. Then, following the treatment of QFT (Quantum Field Theory) [15], we replace.

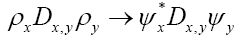
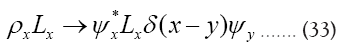
Remark that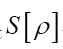 will be replaced by 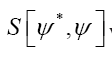which must be even and hermitian. So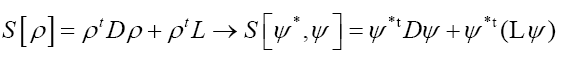

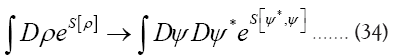
Next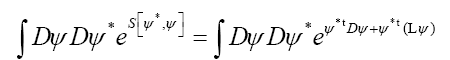

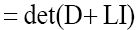
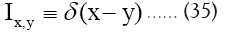
where I is the identity operator and we now replace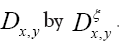

We then get (where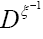 is the inverse of the operator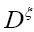

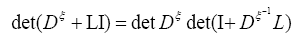
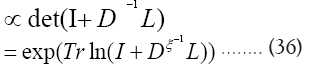
since det 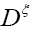does not depend on the and since 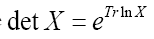for a matrix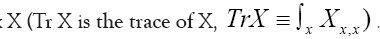

We can write

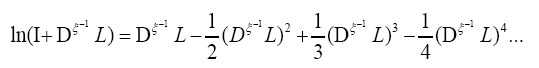
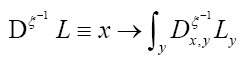
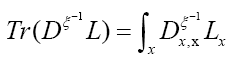
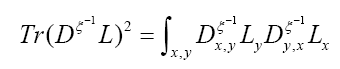
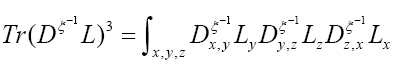
Then using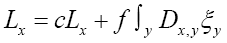

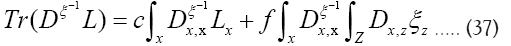
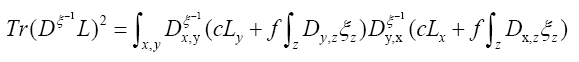
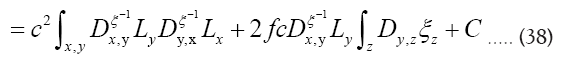
A fermionic action functional and a new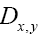

Since 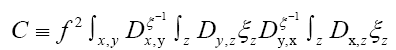does not depend on the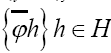

we can dismiss it in equation (38). Next continue with the case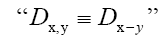 and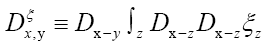 and we define

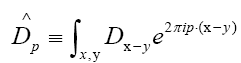
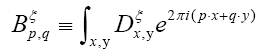
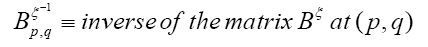
Then for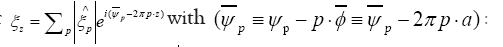

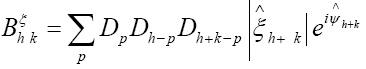
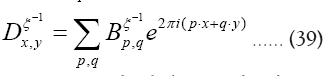
To get some idea let’s consider the simpler case 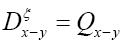but still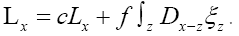

Then the inverse of Q, i.e. Q^-1reads

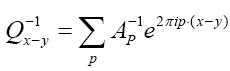
Then

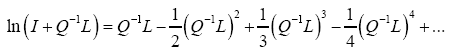
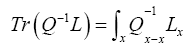
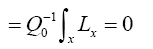
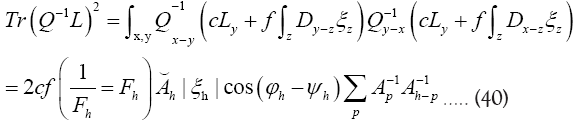
Where we omitted a term in equation (40) that does not depend on ϕ_h. In equation (40) we have used the identities

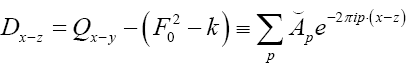
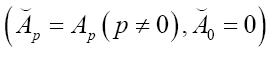
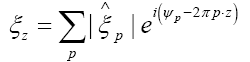
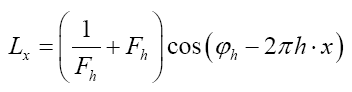
Finally, for 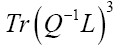we get (omitting the terms that don’t depend on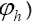

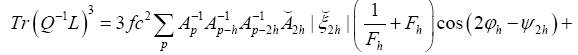
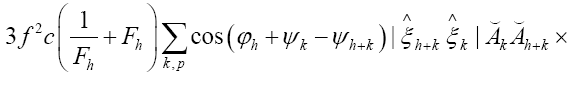
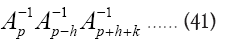
The terms 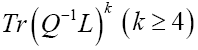are of higher order in f and c. So we see that we obtain in this way a probability of the form and thus

Equation (41) shows that for this model it is advantageous to choose f=c and then to use c for convergence considerations. For example, Equation (42) is then valid up to

We can extend the above model and study instead the model with action.

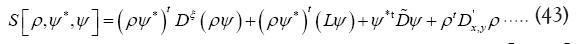
To calculate then the functional integral 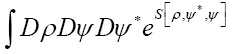we use the following trick.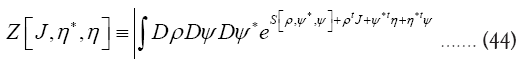

If we then define

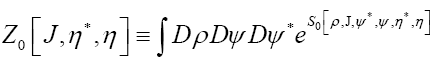
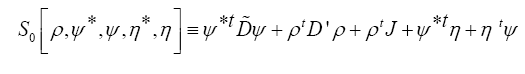
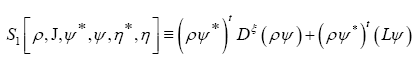
Then

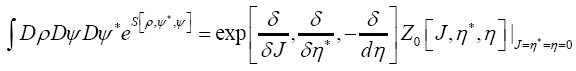
where the choice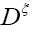 is clear and where we choose 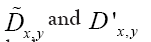and invertible to make calculations easier 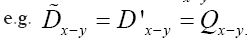Let us define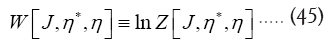

The it can be shown that 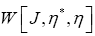contains exactly all the connected diagrams of 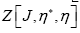[1,15,16]. It is beyond the scope of this article to talk more about diagrams, but we shall discuss it together with the solution in a future paper.

Averaging over gaussian distributions ρ

So far we have been averaging over all positive 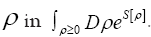But what if we want to average only over gaussian ρ functions? The solution is the functional change of variables 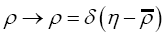where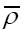 is the true atomic distribution; This substitution is good if we don’t care about N-dependence, if we don’t want N-dependence we should instead consider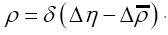

That is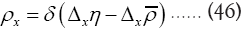

where 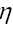is a positive function, our new random variable.

Since 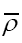and thus also 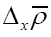is about the true density they are completely determined by the phases 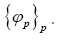In this way we will get a probability distribution of all 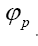Then the “volume” element 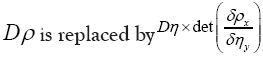, that is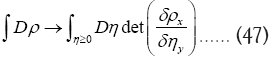

This can be calculated but we can avoid this added complexity if we remark that we could have started from the very beginning by using instead of ρ the more complex form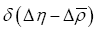 that is we replace 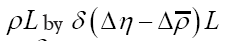and so on. Replacing next the symbol 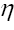by 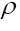we then get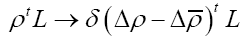 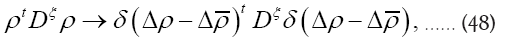etc. In this way the former is now describing “point” particles. However, the whole use of functional integrals in QFT is to describe interactions among point particles. So we do not know if it is worth doing averages over those Gaussian “point” particles.

We close this remark by giving two representations of the δ function. One is to represent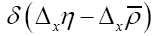 by a gaussian with infinitesimal variance. The other very interesting representation is 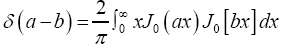In our case it reads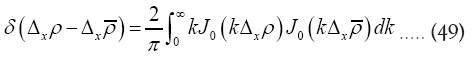

We can then first integrate over ρ and after that perform the integration over k, which is much easier.

Maximality with constraints

We saw in the foregoing sections that we had to maximize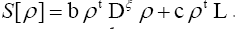 Let us analyze this further. We shall now start with 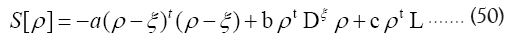We will maximize this with the constraints 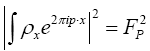for all 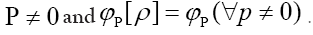Next observe that 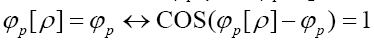We then use the method of Langrangian multipliers. Put now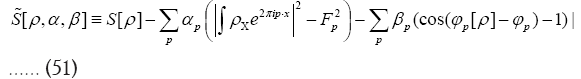

The minus signs in equation (51) have been chosen so as to use later on the more general “KKT- multipliers”) and find the solutions 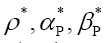for which 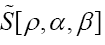is maximal (critical), that is solve the equations

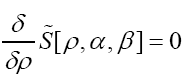
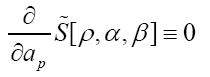
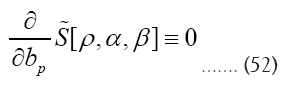
Next

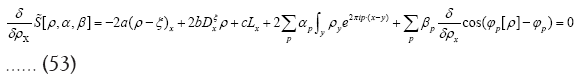
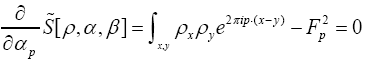
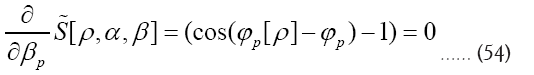
Next observe that

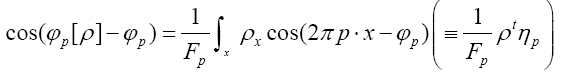
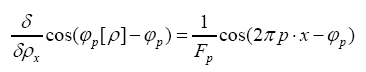
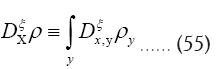
Since 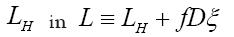has now become redundant, we replace 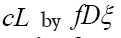in equation (51). We can also add inequality constraints for ρ

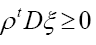
and

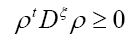
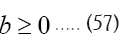
In this case the multipliers 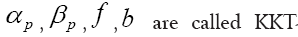multipliers (KKT stands for Karush- Kuhn-Tucker). And we have a dependence 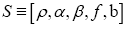now on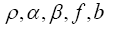

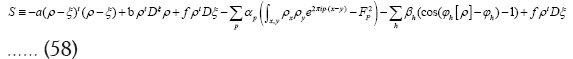
It follows from the above equation that we can impose (we suppose in this paper that friedel’s law is valid, that is 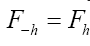and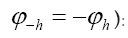

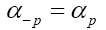
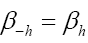
We use the notation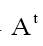 to denote the transpose of A, and then 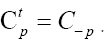We have to solve

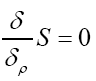
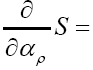
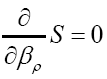
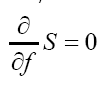
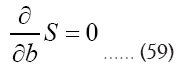
We find

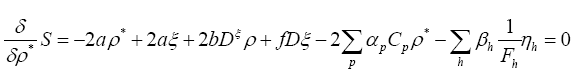
This gives (using ρ* instead of ρ)

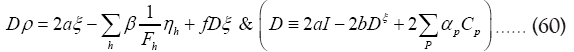
and thus

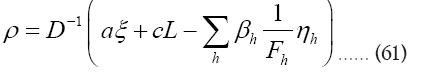
Next we develop [16]

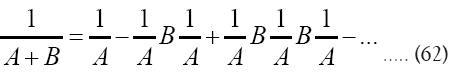
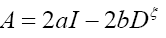
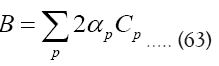
Then,

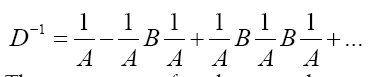
Then we can write if we choose a to be great and b small (a>>b)

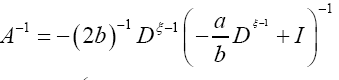
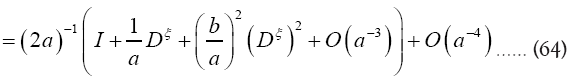
or if we choose a small and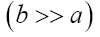

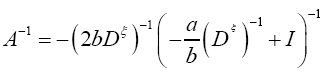
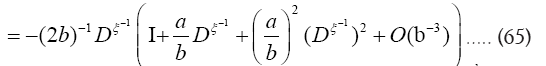
Since we prefer to use the easier 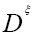instead of 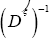we shall in this paper proceed with the development of equation (64). Then for a>>b we find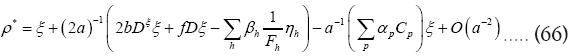

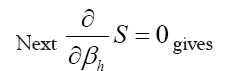
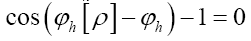
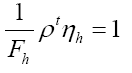
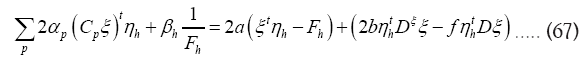
Next 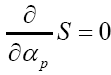will give

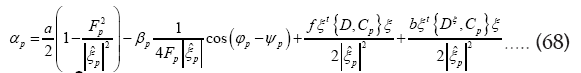
From 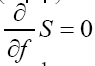follows

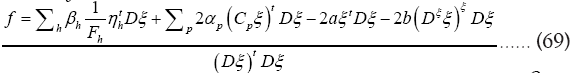
From the equations (67,68) we derive the values of α_p and β_p as functions of f and b. From these results and equation (69) we derive the value of f as a function b. We now see that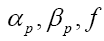 are of order 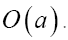. If we would derive the value for b with the condition 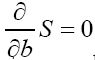then we will also see that b is of order 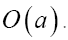which gives a problem since we started with the assumption (a>>b)

For this reason, we shall not impose the condition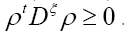 The bare minimum is the calculation of all the Lagrange multipliers 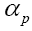and one or more Lagrange multipliers 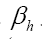All the multipliers depend strongly on the phase invariants 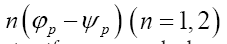The situation becomes even more interesting if one now calculates 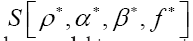and this is good news. We think that this last model is very exciting (perhaps it can even be used to construct the exact ρ from any given ξ). We will study all this in a separate paper.Now 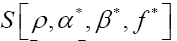can be written in a short way as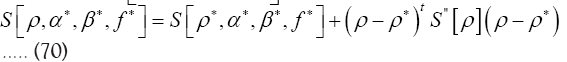

Since 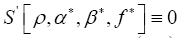and moreover one can verify easily that 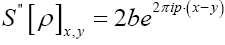is a constant in ρ.

Conclusion

To calculate a probability distribution prob 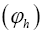for some phase 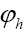one chooses one of the models discussed in this paper and also some of reciprocal vectors containing h. Then one calculates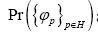 according to the chosen model. After that one calculates the marginal distribution 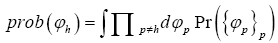Always choose structural information ξ e.g. the fixing of the origin 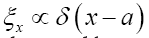All models should lead to the solution of the phase problem.

In a future paper (II) we shall study in detail all different models but especially the fermionic model and the one of maximality with constraints. Especially we shall discuss the most general fermionic model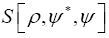 and we shall talk about the technique of the diagrams to calculate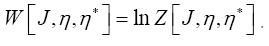

For the very interesting model of maximality with constraints we shall also add the KKT condition 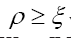with some KKT multiplier 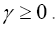Finally, in a last paper (III or IV) we shall test the theory on simulated crystal structures.

We shall also discuss which strategy to use in case of available space group information. Our paper treated only the space P1 (satisfying Friedel’s law). Our use of functional integration and calculus is much more powerful than the other methods of phase determination, be it probabilistic or direct space methods and is valid for any number N of atoms. We shall also try to discuss models for which the formulas will depend N.

References

1. Brosius J. Probability distributions of phases without N. Adv Mathematic Res. 2020;27.
2. Xu H, Weeks CM, Deacon AM, Miller R, Hauptman HA. Ill-conditioned shake-and-bake: The trap of the false minimum. Acta Crystallogr A. 2000;56(2):112-118.

   [Crossref] [Google Scholar] [PubMed]

3. Langs DA, Hauptman HA. Relaxation of the resolution requirements for direct-methods phasing. Acta Crystallogr A. 2011;67(4):396-401.

   [Crossref] [Google Scholar] [PubMed]

4. Bethanis K, Tzamalis P, Hountas A, Mishnev AF, Tsoucaris G. Upgrading the twin variables algorithm for large structures. Acta Crystallogr A. 2000;56(2):105-111.

   [Crossref] [Google Scholar] [PubMed]

5. Burla MC, Camalli M, Carrozzini B, Cascarano GL, Giacovazzo C, Polidori G, et al. SIR2000, a program for the automatic ab initio crystal structure solution of proteins. Acta Crystallogr A. 2000;56(5):451-457.

   [Crossref] [Google Scholar] [PubMed]

6. Altomare A, Burla MC, Camalli M, Cascarano GL, Giacovazzo C, Guagliardi A, et al. SIR97: A new tool for crystal structure determination and refinement. J Appl Cryst. 1999;32(1):115-119.

   [Crossref] [Google Scholar]

7. Burla MC, Camalli M, Carrozzini B, Cascarano GL, Giacovazzo C, Polidori G, et al. SIR99, a program for the automatic solution of small and large crystal structures. Acta Crystallogr A. 1999;55(6):991-999.

   [Crossref] [Google Scholar] [PubMed]

8. Cascarano G, Giacovazzo C, Camalli M, Spagna R, Burla MC, Nunzi A, et al. The method of representations of structure seminvariants. The strengthening of triplet relationships. Acta Crystallogr A. 1984;40(3):278-283.

   [Crossref] [Google Scholar]

9. Burla MC, Carrozzini B, Cascarano GL, Comunale G, Giacovazzo C, Mazzone A, et al. Estimates of triplet invariants given a model structure. Acta Crystallogr A. 2012;68(4):513-520.

   [Crossref] [Google Scholar]

10. Giacovazzo C. Direct phasing in crystallography: Fundamentals and applications. Oxford Univers Press. 1998.

    [Google Scholar]

11. Gradshteyn IS, Ryzhik IM. Table of integrals, series, and products. Academic Press. 1980.

    [Crossref]

12. Frank WO, Daniel WL, Ronald FB, Charles WC. NIST handbook of mathematical functions. Cambridge Univers Press. 2010.

    [Google Scholar]

13. Diener F, Reeb G. Analyse non standard. 1989. [Google Scholar]
14. Nelson E. Internal set theory: A new approach to nonstandard analysis. Bull Amer Math Soc. 1977;83(6):1165-1198.

    [Crossref] [Google Scholar]

15. Weinberg S. The quantum theory of fields. Cambridge University Press. 2005.

    [Google Scholar]

16. Siegel W. Fields. 2005.
17. Kuzenko SM, Buchbinder IL. Ideas and methods of supersymmetry and supergravity or a walk through superspace. 1998.

    [Crossref] [Google Scholar]

18. Bruhat YC, Bleick MD, Morette CD. Analysis, manifolds and physics. 2000.

    [Crossref] [Google Scholar]

19. deWitt BS. Supermanifolds. 1992.

    [Crossref] [Google Scholar]