Mathematica Eterna
Open Access

Probability Density Function: Illuminating the Spectrum of Statistical Distributions

Bertram George^{* *}Correspondence: Bertram George, Department of Mathematics, Roma Tre University, Roma, Italy, Email:

Author info »

Introduction

In the realm of probability theory and statistics, the concept of a Probability Density Function (PDF) serves as a cornerstone for understanding the likelihood of continuous random variables. As a mathematical tool, the PDF provides a framework for characterizing the distribution of probabilities within a given range. In this article, we delve into the intricacies of probability density functions, exploring their definition, properties and diverse applications across various fields of study.

Description

Defining probability density function

A probability density function is a mathematical function that describes the likelihood of a continuous random variable falling within a particular range. Unlike discrete probability distributions that deal with distinct outcomes, a PDF is associated with continuous random variables, offering a smooth representation of the probabilities over a range of values.

Mathematically, for a continuous random variable x, the PDF is represented by the function f(x), where f(x) ≥ 0 for all x and the total area under the curve of f(x) over its entire range is equal to 1. The probability of X falling within a specific interval

(a,b) is given by the integral of f(x) over that interval:

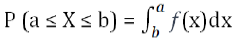
Properties of probability density function

Non-negativity: The PDF, denoted as f(x), is non-negative for all values of x. That is, f(x) ≥ 0 for all x.

Total area under the curve: The total area under the PDF curve over its entire range is equal to 1. This reflects the notion that the sum of all possible probabilities for a continuous random variable is unity.

Probability within an interval: The probability of a continuous random variable falling within a specific interval (a,b) is given by the integral of the PDF over that interval.

Probability at a point: The probability of a continuous random variable taking a specific value c is zero. Mathematically, P(X=c)=0. This is because the likelihood of hitting an exact point in a continuous distribution is infinitesimally small.

Applications in statistics

Normal distribution: The PDF is prominently used in describing the normal distribution, also known as the Gaussian distribution or bell curve. The normal distribution's PDF is characterized by its symmetrical, bell-shaped curve, providing a robust model for various natural phenomena.

Exponential distribution: The exponential distribution, commonly used in survival analysis and reliability engineering, relies on the PDF to describe the probability of the time until an event occurs.

Uniform distribution: In the uniform distribution, all values within a given interval have equal probabilities. The PDF for a uniform distribution is a constant function.

Beta distribution: The beta distribution, often used in Bayesian statistics, has a PDF that represents the probability distribution of a random variable constrained to intervals between 0 and 1.

Chi square distribution: The chi square distribution, frequently employed in statistical hypothesis testing, utilizes the PDF to model the distribution of the sum of squared standard normal deviates.

Cauchy distribution: The Cauchy distribution, known for its heavy tails, utilizes the PDF to depict the probability distribution of a continuous random variable.

Applications in physics and engineering

Quantum mechanics: In quantum mechanics, the wave function serves as a probability amplitude. The square of the absolute value of the wave function gives the probability density, akin to a PDF, for finding a particle at a particular location.

Signal processing: In signal processing, PDFs are employed to model the distribution of signal amplitudes or noise, aiding in the design and analysis of communication systems.

Reliability engineering: PDFs play a crucial role in reliability engineering by modeling the time until failure of a system or component. This is vital in assessing the reliability and durability of various engineering systems.

Finance and economics: Probability density functions are applied in modeling financial data, such as stock prices and interest rates. They help analysts and economists understand and predict market behaviors.

Conclusion

Probability density functions stand as a fundamental tool in probability theory and statistics, providing a sophisticated means of characterizing the likelihood of continuous random variables. From the elegant symmetry of the normal distribution to the versatility of other distributions in modeling real-world phenomena, PDFs offer a powerful lens through which to analyze, interpret and make predictions about diverse datasets. As the foundation of countless statistical methods and models, probability density functions continue to play a pivotal role in unraveling the mysteries of uncertainty across a multitude of disciplines.