Mathematica Eterna
Open Access
ISSN: 1314-3344
ISSN: 1314-3344
Research - (2019)Volume 9, Issue 1
In this paper, some generalizations of the classical polarization formula are used to recover the relative phase in phase retrieval problem. Theoretically, in order to reconstruct any signal from its intensity measurements by polarization formula, the amount of needed measurements can be same as PhaseLift method. The numerical simulation also illustrates its good effect in (affine) phase retrieval with additive white Gaussian noised intensity Fourier measurements.
Polarization formula; Phase retrieval; Frame 2010 MS Classification 42C15
The aim of phase retrieval is to recover signal x from its intensity
measurements 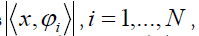 where
where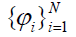 forms a frame of Cd. Since
forms a frame of Cd. Since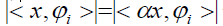 for any
for any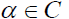 with
with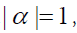 the best reconstruction of x is up to a unimodular
constant. Phase retrieval arises in many areas of engineering and
applied physics, including X-ray crystallography [1-8], optics [9],
and computational biology [10-13]. In fact, it is difficult to solve
the phase retrieval problem if one only knows the intensity
measurements. One way to overcome this issue is to collect more
prior information of the signal x [11]. Another way is to take more
additional measurements. We only mention two different methods
of the second way. The PhaseLift algorithm is proposed by Candès
et al. with the lift technique of semi-definite programming [6].
Polarization method using structured measurements is proposed by
Alexeev et al. [2]. Natural nonconvex algorithms often work remarkably well in practice,
but lack clear theoretical explanations, therefore Sun et al. give a
geometric analysis of phase retrieval [14]. Recently, phase retrieval
in infinite dimensional space also attracts great attentions.
Reconstruction of a bandlimited real-valued function f from
unsigned intensity measurements is considered [8]. Unlike the
finite dimensional case, phase retrieval in infinite dimensional
Hilbert space is never uniformly stable [4]. Therefore, Alaifari et al.
proposed a new paradigm for stable phase retrieval by considering
the problem of reconstructing signal up to a phase factor that is
not global [1].
the best reconstruction of x is up to a unimodular
constant. Phase retrieval arises in many areas of engineering and
applied physics, including X-ray crystallography [1-8], optics [9],
and computational biology [10-13]. In fact, it is difficult to solve
the phase retrieval problem if one only knows the intensity
measurements. One way to overcome this issue is to collect more
prior information of the signal x [11]. Another way is to take more
additional measurements. We only mention two different methods
of the second way. The PhaseLift algorithm is proposed by Candès
et al. with the lift technique of semi-definite programming [6].
Polarization method using structured measurements is proposed by
Alexeev et al. [2]. Natural nonconvex algorithms often work remarkably well in practice,
but lack clear theoretical explanations, therefore Sun et al. give a
geometric analysis of phase retrieval [14]. Recently, phase retrieval
in infinite dimensional space also attracts great attentions.
Reconstruction of a bandlimited real-valued function f from
unsigned intensity measurements is considered [8]. Unlike the
finite dimensional case, phase retrieval in infinite dimensional
Hilbert space is never uniformly stable [4]. Therefore, Alaifari et al.
proposed a new paradigm for stable phase retrieval by considering
the problem of reconstructing signal up to a phase factor that is
not global [1].
In this paper, the frame theory is used to obtain some polarization
identities. At first, we briefly introduce some definitions and
notations. Let H denotes a separable Hilbert space with the inner
product 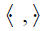 and J be a countable index set.
and J be a countable index set.
Definition 1.1. A sequence 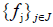 of elements in H is a frame for H
if there exists constants A, B > 0 such that
of elements in H is a frame for H
if there exists constants A, B > 0 such that
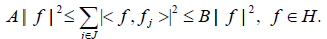
The constants A, B are called lower and upper frame bounds for the frame. A frame is A-tight, if A=B. If A =B=1, it is called a Parseval frame.
Frame theory not only provides an effective analysis method for
signal processing, but also offers a reconstruction method. We
call 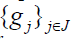 a dual frame of
a dual frame of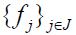 if it is a frame for H and
satisfying
if it is a frame for H and
satisfying

The dual frame always exists but generally not unique. Since 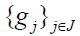 is also a frame, the function f has the expression
is also a frame, the function f has the expression 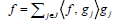 as well. For special case, if
as well. For special case, if is an A-tight frame,
then
is an A-tight frame,
then 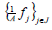 is a dual frame. And if
is a dual frame. And if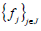 is a Parseval frame, it is a
dual frame of itself.
is a Parseval frame, it is a
dual frame of itself.
Since the complex field C is closely related to the Euclidean
space R2, the frame theory in R2 can be rewritten with respect to
complex numbers. Explicitly, any complex number Z=X+IY can be
considered as a bidimensional vector (x, y). Therefore, for any two
complex numbers z1 and z2, the real part 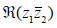 is an inner product of the vectors with respect to them. Without confusion, we call the
collection
is an inner product of the vectors with respect to them. Without confusion, we call the
collection 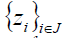 is a frame for C if its corresponding collection
of vectors is a frame for R2. And the frame reconstruction formula
can be rewritten as
is a frame for C if its corresponding collection
of vectors is a frame for R2. And the frame reconstruction formula
can be rewritten as

where {z˜k }k∈J is the dual frame of {zk }k∈ J. Some polarization identities and examples are given in Section 2. We discuss the applications of polarization identities in (affine) phase retrieval problem in Section 3.
Polarization Formulas
In this section, we show some polarization identities that are deduced from frame theory in C. The classical polarization identity in functional analysis becomes a special case.
Lemma 2.1. Suppose 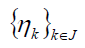 is a frame for C with dual frame
is a frame for C with dual frame
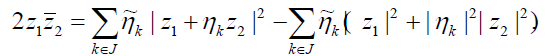
Proof. We expand the modulus:
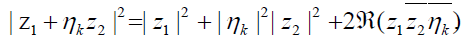
Taking summation over k and applying reconstruction formula (1.2) to the expansion, we get the desired result.
Above lemma can be generalized to any Hilbert space to get a polarization identity with similar proof.
Theorem 2.1. Suppose 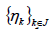 is a frame for C with dual frame
is a frame for C with dual frame 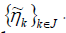 . Then for any two elements f, g in a Hilbert space H, we
have
. Then for any two elements f, g in a Hilbert space H, we
have
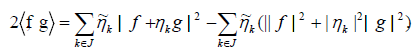
By imposing some constraints to the frames, we can get some
compact results. For instance, if 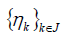 is an equal norm frame
that is
is an equal norm frame
that is  for some constant c > 0 and all k ∈ J, then we have
for some constant c > 0 and all k ∈ J, then we have
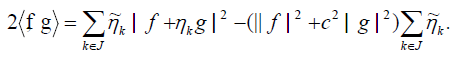
Furthermore, if we require 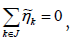 then
then

Even more, if 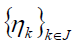 is an A-tight frame, then the expression is
not related to dual frame in form. Explicitly, we have
is an A-tight frame, then the expression is
not related to dual frame in form. Explicitly, we have
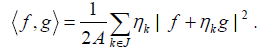
All the above polarization identities can be generalized to sesquilinear form. We only show the last one in the following.
Theorem 2.2. Let W be a complex vector space, S a sesquilinear
form on W, and q the quadratic form generated by S. Suppose 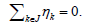 is an A-tight equal norm frame for W with
is an A-tight equal norm frame for W with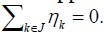 Then we have
Then we have
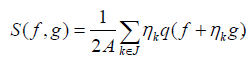
This theorem is easy to prove. From the theorem of Jordan and Von Neumann, we know that a norm on a vector space is generated by an inner product if and only if the parallelogram is satisfied. If this is so then the inner product is given by (2.7). In fact, one can prove that the inner product is also given by any frame in Theorem 2.1.
One important thing is whether an equal norm tight frame exists. The answer is positive and explicit constructions are given in finite frames: theory and applications [7] and reference therein. In the rest of this section, we consider the frame that consists of Nth roots of unity.
Lemma 2.2. Let 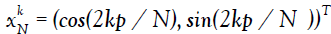 for N ≥ 3, then
for N ≥ 3, then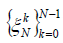 is an equal norm tight frame for R2 with frame
bound N/2 and satisfy
is an equal norm tight frame for R2 with frame
bound N/2 and satisfy 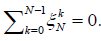
Proof. For any f = (x, y)∈R2 with norm 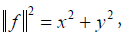 there exists
an angle θ such that
there exists
an angle θ such that 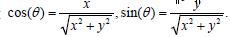 Then we have
Then we have
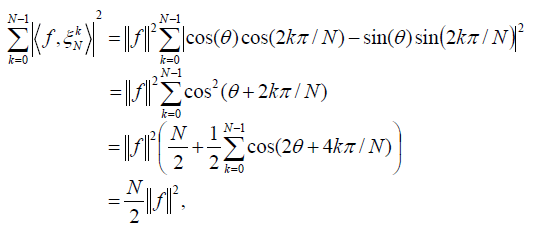
where the equation 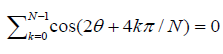 is used in the last
equation.
is used in the last
equation.
By the frame properties we have
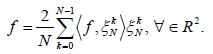
As mentioned before, there is an equivalent formula corresponding to complex field C. Explicitly, for any complex number z, we have

where 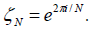 Taking
Taking 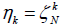 in Lemma 2.1 and Theorem 2.1,
we get the following two corollaries.
in Lemma 2.1 and Theorem 2.1,
we get the following two corollaries.
Corollary 2.1. Take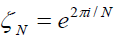 for N ≥ 3. Then for any
for N ≥ 3. Then for any 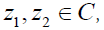

Corollary 2.2. Let H be a complex Hilbert space and 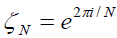 for N ≥ 3. Then for any f, g ∈ H,
for N ≥ 3. Then for any f, g ∈ H,

Taking N = 3 in Corollary 2.1, we get the polarization identity stated [2]. The classical polarization formula in functional analysis is a special case of Corollary 2.2 with N = 4, that is

Consequently, the above corollaries can be viewed as a generalization of the canonical polarization formula.
The frames consisted of Nth roots of unity play an important role
in above discussion. Since it’s not very efficient in phase retrieval
when N is large, reduction of elements in frame is needed. In fact,
three elements of the Nth roots are enough for recovering the
inner product. Let k1,k2,k3 be any three different integers in the set {0,1,...,N −1}. Then 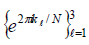 must form a frame for C. If there
exists a dual frame
must form a frame for C. If there
exists a dual frame  satisfying
satisfying

Then we get a reconstruction formula

In fact, if we write 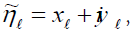 since the reconstruction
formula holds if and only if it holds for f =1 and f=i by linearity of
innerproduct, the equations (2.8) and (2.9) are equivalent to the
matrix equation XA = B, where
since the reconstruction
formula holds if and only if it holds for f =1 and f=i by linearity of
innerproduct, the equations (2.8) and (2.9) are equivalent to the
matrix equation XA = B, where
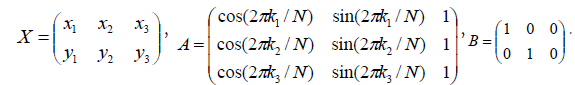
If A is invertible, the matrix equation has a unique solution and the corresponding dual frame satisfy (2.8) and (2.9). By simple computation, we have
det A= 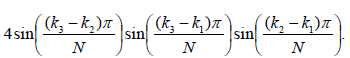
Since k1, k2, k3 are different from each other in the set {0,1,...,N −1}. the determinant of matrix A is not zero.
Combing the above discussion, we have the following conclusion:
Theorem 2.3. Suppose k1, k2, k3 are three different integers from
each other in the set {0,1,...,N −1}. Then, the collection 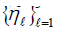 forms
a frame of C with a dual frame
forms
a frame of C with a dual frame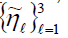 satisfying (2.8) and (2.9).
satisfying (2.8) and (2.9).
Example 2.1. The Nth roots of unity are 1, i, −1, −i when N = 4. By Theorem 2.3, we can find four frames of C and their corresponding dual frames, which are listed in Table 1. As a result, we can get four polarization identities by formula (2.3). The first one is given by

The others can be written out similarly.
If we continue to reduce the number of elements in a frame to two,
then the new frame should be a basis of C and have no redundancy.
Therefore, the restriction 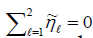 is no longer hold. However,
we still can recover the innerproduct by the following theorem
whose proof is similar to Theorem 2.3.
is no longer hold. However,
we still can recover the innerproduct by the following theorem
whose proof is similar to Theorem 2.3.
Theorem 2.4. Taking out two numbers k1 ,k2 from the set {0,1,...,N −1} with 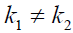 if N is odd and
if N is odd and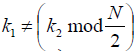 if N is even, then we have that the set
if N is even, then we have that the set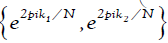 forms a
frame with dual frame
forms a
frame with dual frame 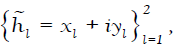 which is given by
which is given by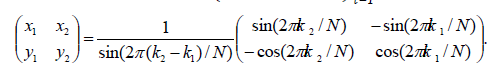
Example 2.2. The Nth roots of unity are 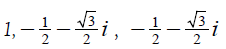 when N=3. By Theorem 2.4, we get three frames and their dual frames, which are listed in Table 2. As a result, we can get three polarization
identities by Theorem 2.1. The first one is given by
when N=3. By Theorem 2.4, we get three frames and their dual frames, which are listed in Table 2. As a result, we can get three polarization
identities by Theorem 2.1. The first one is given by
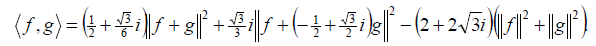
The others can be written out similarly.
In Example 2.2, the expression of polarization identity is not likely to become easier than Example 2.1. However, in phase retrieval, since the original intensity measurements ∥f ∥2 , ∥g∥2 are known generally, only two additional measurements are needed in order to recover relative phase.
Applications To Phase Retrieval
In this section, we apply the polarization identities to phase retrieval problem. The key ingredient is to add new measurements in order to gain the relative phase.
By leveraging the ideas of Alexeev et al. [2] and Bandeira et al.
[3], we can implement polarization algorithms in phase retrieval
problem with the help of polarization identities that are given in
Section 2. Suppose the intensity measurements 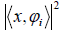 are known,
the key point to recover signal x with polarization method is to
compute the relative phase using
are known,
the key point to recover signal x with polarization method is to
compute the relative phase using 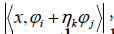 where
where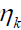 is a frame
of C. If
is a frame
of C. If 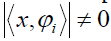 and
and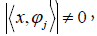 the relative phase between
the relative phase between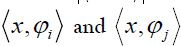 is defined by
is defined by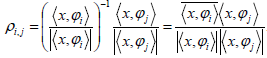
Since 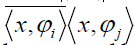 can be considered as an innerproduct in C,
it can be computed by Lemma 2.1. If
can be considered as an innerproduct in C,
it can be computed by Lemma 2.1. If 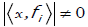 for every i∈ J , we
can get the relative phase
for every i∈ J , we
can get the relative phase 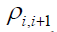 of two adjacent points, or relative
phase
of two adjacent points, or relative
phase 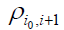 of two points with
of two points with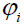 is fixed. Then the signal x can
be recovered up to a global phase factor. In graph theory terms, if
the graph with vertex
is fixed. Then the signal x can
be recovered up to a global phase factor. In graph theory terms, if
the graph with vertex 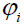 and edges x is a circle or star, then we
can recover x . However, in general situation, there is a mask
and edges x is a circle or star, then we
can recover x . However, in general situation, there is a mask 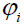 orthogonal to the signal x i.e.,
orthogonal to the signal x i.e.,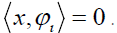 Therefore the relative
phases can’t propagate across this vertex. The authors of Alexeev
et al. [2] propose to design full spark frame and expander graph to
overcome this shortage.
Therefore the relative
phases can’t propagate across this vertex. The authors of Alexeev
et al. [2] propose to design full spark frame and expander graph to
overcome this shortage.
In this section, we focus on phase retrieval simulations with masked Fourier measurements, which are obtained by measuring the Fourier power spectrum of signals with adding mask. In order to have a high probability recovery, the mask is chosen randomly with Gaussian distribution.
Let 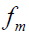 denote the complex sinusoid
denote the complex sinusoid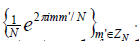 Then the
discrete Fourier transform
Then the
discrete Fourier transform 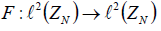 is defined by
is defined by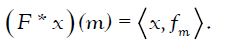
Suppose the Fourier intensity measurements 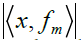 are known,
additional measurements are needed to recover the relative phase.
Taking
are known,
additional measurements are needed to recover the relative phase.
Taking  then we have
then we have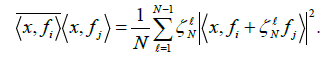
Accordingly, we need N additional vectors 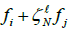 for computing
every relative phase
for computing
every relative phase  Since
Since 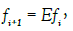 where
where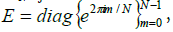 one has
one has
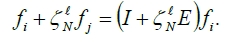
If all intensity measurements 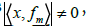 then we need N + 1 masks
then we need N + 1 masks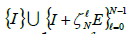 to recover x . By Theorem 2.3, one can reduce the
number of total masks to four. When the intensity measurements
to recover x . By Theorem 2.3, one can reduce the
number of total masks to four. When the intensity measurements 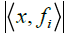 are known, one can continue to reduce the amount of masks
to three by Theorem 2.4. For instance, we can take the masks as in
Example 2.2, and then the total masks are
are known, one can continue to reduce the amount of masks
to three by Theorem 2.4. For instance, we can take the masks as in
Example 2.2, and then the total masks are 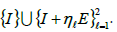 Comparing
with the masks
Comparing
with the masks 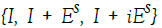 in Candes et al. [5], the same
amount of masks are used.
in Candes et al. [5], the same
amount of masks are used.
We demonstrate the performance of polarization method with
different frames and their duals in phase retrieval problem. Given
a random signal, we add white Gaussian noise with different noise
level to the intensity measurements such that the signal noise ratio
(SNR) changes from 13 to 40 with step length 3. The effects of
recovering the original signal with different frames are shown in Table 3, where 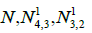 correspond to N-th roots of unity frames,
the first frame in Table 1 and Table 2 respectively. Observing Table
3, we find that the polarization method also have denoising effects
due to the least square method that is used in the reconstruction
process. For different frames, it seems that the effects have not much difference. However, for large N, we can still recover the
signal when erasures occur in intensity measurements.
correspond to N-th roots of unity frames,
the first frame in Table 1 and Table 2 respectively. Observing Table
3, we find that the polarization method also have denoising effects
due to the least square method that is used in the reconstruction
process. For different frames, it seems that the effects have not much difference. However, for large N, we can still recover the
signal when erasures occur in intensity measurements.
| Four frames | Dual frames |
| 1, i, -1 | 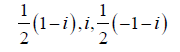 |
| 1, i, -i | 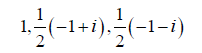 |
| 1, -1, -i | 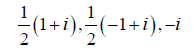 |
| i, -1, -i | 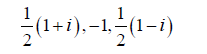 |
Table 1: Four frames and their dual frames.
| Three frames | Dual frames |
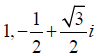 |
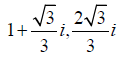 |
 |
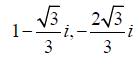 |
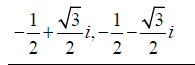 |
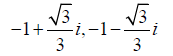 |
Table 2: Three frames and their dual frames.
|    SNR/ Frames |
13 | 16 | 19 | 22 | 25 | 28 | 31 | 34 | 37 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|
| N=3 | 17.1 | 20.2 | 21.9 | 25.0 | 26.4 | 29.0 | 32.7 | 37.0 | 39.9 | 40.8 |
| N=4 | 17.5 | 20.0 | 23.7 | 24.8 | 29.6 | 30.2 | 30.8 | 33.9 | 40.1 | 41.9 |
| N=5 | 17.5 | 19.5 | 22.5 | 26.4 | 26.8 | 29.9 | 31.3 | 35.4 | 40.0 | 43.1 |
| N=6 | 18.1 | 18.7 | 23.0 | 24.0 | 27.4 | 31.0 | 34.6 | 36.4 | 38.5 | 43.8 |
| N=7 | 17.3 | 19.9 | 23.2 | 25.0 | 27.3 | 30.9 | 33.3 | 36.8 | 38.3 | 41.0 |
| N=8 | 17.5 | 20.0 | 21.4 | 24.5 | 28.8 | 31.2 | 32.6 | 36.1 | 40.0 | 39.6 |
| N=9 | 15.8 | 20.5 | 22.9 | 23.2 | 28.3 | 28.2 | 33.0 | 37.3 | 40.0 | 39.9 |
| N=10 | 17.8 | 20.3 | 21.5 | 27.7 | 26.0 | 32.0 | 33.4 | 36.7 | 40.2 | 42.5 |
| N14,3 | 19.6 | 22.8 | 23.6 | 23.5 | 27.6 | 28.3 | 30.2 | 38.2 | 38.6 | 41.3 |
| N13,2 | 17.1 | 19.1 | 23.6 | 24.8 | 27.3 | 30.2 | 33.2 | 33.2 | 37.8 | 41.5 |
Table 3: Effects of different frames with different noise level measured by decibel.
Affine phase retrieval introduced in Gao et al. [10] has an exact reconstruction but not up to a unimodular constant. Explicitly, we consider recovering signal from the absolute values of the affine linear measurements
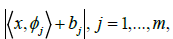
where 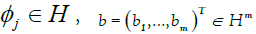 and H = C or R. Let
and H = C or R. Let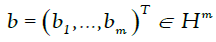 and
and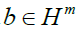 , by vector augmentation, we
set
, by vector augmentation, we
set
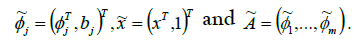
Then the measurements can be written as 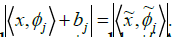 One can prove easily that (A,b) is affine phase retrievable if A and A˜ are both full spark. Generally, the polarization method is
hardly used to high dimension data due to its high computation
complexity. However, because of the exact reconstruction of affine
phase retrieval, this can be implemented by affine phase retrieval in
one dimension iteratively. As a simulation, the polarization method
is used to reconstruct the cameraman image from its power spectrum
with SNR=20. This is implemented by reconstruction column by
column in one dimension. Finally, we get the reconstructed image
with SNR=17.9, which is illustrated in Figure 1.
One can prove easily that (A,b) is affine phase retrievable if A and A˜ are both full spark. Generally, the polarization method is
hardly used to high dimension data due to its high computation
complexity. However, because of the exact reconstruction of affine
phase retrieval, this can be implemented by affine phase retrieval in
one dimension iteratively. As a simulation, the polarization method
is used to reconstruct the cameraman image from its power spectrum
with SNR=20. This is implemented by reconstruction column by
column in one dimension. Finally, we get the reconstructed image
with SNR=17.9, which is illustrated in Figure 1.

Figure 1: The left is the original image, right is the reconstruction image from intensity measurements with SNR=20.
By the advantage of frame theory, a class of generalization of polarization formula is given, which makes the classical polarization as a special case. It provides a strong support for recovering the relative phase in polarization method. Furthermore, the same amount of intensity measurements are used as in PhaseLift method. The numerical simulations also demonstrate its good effect in (affine) phase retrieval of signal and image with Fourier measurements.
Acknowledgements
The authors would like to thank the referees for their useful comments and remarks.
Availability of data and materials
The [cameraman.tif] data used to support the findings of this study are available from the corresponding author upon request.
Funding
This study was partially supported by National Natural Science Foundation of China (Grant No.11601152).
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to this work. All authors read and approved the final manuscript.
Citation: Zhuang Z, Wu G (2019) A Generalization of Polarization Formula and Its Application in Phase Retrieval. Mathematica Eterna. 9:101.
Received: 03-May-2019 Accepted: 22-Jul-2019 Published: 29-Aug-2019
Copyright: © 2019 Zhuang Z, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.