Journal of Osteoporosis and Physical Activity
Open Access
ISSN: 2329-9509
ISSN: 2329-9509
Research Article - (2016) Volume 4, Issue 3
The density of minerals in bone can be measured by Bone Densitometry. The minerals in the bone are used to estimate the fracture risk due to osteoporosis in people of all age groups. Osteoporosis causes the decrease in mineral density of bone due to formation of minute holes (loss of bone) in bone. Osteoporotic fractures are a vital public health concern, early diagnosis of persons with higher risk of osteoporosis can help them free from future onset of multiple and sudden fractures in bone. This study is carried out by using Finite Element Analysis (FEA) on femur bones under static condition. Finite Element Analysis had been widely used to understand the mechanical behavior of femur bones of various age groups from the images developed by Computed Tomography (CT) Scans. In this work three dimensional models of the human femur bones were developed by using MIMICS software and Finite Element (FE) analysis was carried out by using COMSOL 5.0 Multi physics software. The results obtained were compared with WHO standards. These results indicate a correlation between bone densitometry values of various age groups and the computed stress T-score values from the models. This work can act as a new approach to find bone density, predicting the type of fractures and onset of osteoporosis in the bones.
<Keywords: Bone density; Osteoporosis; Finite element analysis; T-Scores
Biomechanics is the study of science concerned with internal and external forces acting on the human body and the effects of forces on bone. Biomechanics uses the tools of mechanics which is a branch of physics involving the analysis of forces, to study anatomical and functional aspects of living organisms. Computer simulation has become an essential part of science and engineering. Digital analysis of components, in particular, is important while developing new products or optimizing designs. The advanced technology in medical field has been becoming a revolution in conducting surgical operations. This advanced technology helps to a lot in optimizing the results and also it reduces complexity in analysis. Especially in medical field integration of advanced technologies is considered as an important tool while facing complex situations. This technology that has been adapted in the medical sciences, altogether with the combination of biology and mechanics named as biomechanics.
The femur bone is the second largest and strongest bone in our body as shown in Figure 1 [1]. Thus it requires maximum amount of forces to break the bone. Fracture occurs in femur bone only when the bone is affected with great force due to bending and twisting actions.
Fractures in femur bone are divided according to anatomic regions.
• Fractures that occur at the upper end of femur head commonly referred as hip fractures.
• Fractures that occurs at the femoral shaft (between the upper end and lower end of femur bone).
• Fractures that occur just above the knee region commonly known as supracondylar femur fractures.
Various types of fractures that occur at various locations of a femur bone are shown in Figure 2 [2]. Fracture that occurs just below at the spherical head region of a bone as shown in the first bone which is known as sub capital neck fracture. Second bone defines the fracture at neck region called as Trans cervical neck fracture. Third bone shows fracture that happens at intertrochanteric line of femur bone known as Intertrochanteric fracture. The fourth bone shows the fracture that happens at sub trochanteric region named as subtrochanteric fracture, Fracture that happens at greater trochanter region shown in fifth bone is known as fracture at greater trochanter, in sixth bone fracture takes place at lesser trochanter region named as lesser trochanter fracture. These are the different types of the fractures, which generally occurs in human femur bone due to sudden and uneven forces and loads acting on the hip joint.
The most common types of femur fractures that occur are at femoral neck region and lower trochanter region. Femoral neck is the region which connects the shaft of femur bone to its round head that fits into a hip joint. Femoral neck is the region which is basically weak due to its small cross sectional area and also due to presence of cancellous bone.
The bone loss resulting from elimination of habitual mechanical loading is the region specific and associated with the degree of immobilization. In the past decade, densitometry has been increasingly used to document these degenerative changes. Most of the research studies have reported changes in bone mass of the hip, with the standard densitometric measurement test, and several reports are available with regards to changes in total leg bone mass, determined from whole body densitometry. While much has been learned about skeletal response to paralysis from these studies, the utility of these data for assessing specific fracture risk is limited. Accurate determination of fracture risk should be based on regional change in bone mass. Bone mass is generally expressed as Bone Mineral Content (BMC) and Bone Mineral Density (BMD). BMD is commonly equated with bone strength in clinical prediction of fracture risk. Osteoporosis is diagnosed by having a simple test that measures bone mineral density sometimes called as BMD [3]. BMD is the amount of bone you have in a given area which is measured at different parts of the human body. Often the measurements are at spine and hip, including a part of the hip called the femoral neck located at the top of the thigh bone (femur). The density of the bone defines the strength of minerals present in a bone. Different equipments made by different companies can give us different measurements and finally the results become misleading. Carvey and Delaney [4] have proposed an outline importance of Bone Mineral Density. According to their study, Bone mineral density (BMD) can be measured by a variety of techniques at several skeletal sites. BMD is used to calculate a T-score and/or Z-score. Both T-scores and Z-scores are derived by comparison to a reference population on a standard deviation scale. This is defined as the bone mineral density that can be compared to the normal young adult of the same age group. It is a comparison of a person’s bone mineral density to that of a healthy twenty five year of same gender. Bone Density can be measured in the form of T-score chart. Bone Density can be measured in the form of T-score chart as shown in Figure 3 [5]. T-scores and Z-scores are widely quoted in scientific publications on osteoporosis and BMD studies. Errors in BMD measurement, differences in reference populations, and variations in calculation methods used, can all affect the actual T-score and Z-score value. According to the World Health Organization (WHO) osteoporosis diagnosis and National Health and Nutritional Examinations Survey reports on T-score and Z-score values, the T-score value is considered as the most relevant measure while diagnosing for osteoporosis.
Figure 4 [6] describes the T-score range of different age group people specified by WHO. According to this standards if the T-score is greater than ‘-1’ then it will be considered as normal bone. If the T-score lies in between -1 to -2 then it will be considered as low bone mass, if the value less than ‘-2’ then it is indicates that the person is suffering with the osteoporotic disease.
Evans and Mcgrory [7] in their research work had stated that between 220,000 and 250,000 femoral fractures that occur in the United States every year 90% of these fractures occur in patients older than 50 years. Their research on femur fractures clearly indicates that femoral fractures at younger age groups are only reported due to high energy physical trauma resulting from high speed motor vehicle accidents. They also highlighted in their research that these types of fractures are more common in women than in men.
The main causes of femoral fractures are stated to be osteoporosis, a maternal history of hip fractures, excessive alcoholic consumption, high caffeine intake, physical inactivity, low body weight, previous hip fracture, use of certain psychotropic medications, visual impairment and dementia [8-13].
The importance of advanced research in fractures related by femur stresses the need to develop a suitable strategy to identify a particular type of fracture in femur. A lot of research is presently being undertaken by using Finite element analysis (FEA) for the selection of appropriate surgical procedure to be adopted as well as in identifying a suitable implant material such as a bone plate or a type of screw or nail. This analysis would be helpful to the surgeons as it would prevent unnecessary pain, proper fixation of the bone and in worst scenario resurgery to fix the fracture. FEA also takes into account a lot of parameters such as loading conditions, stress at the joint, Youngs modulus and mechanical properties of the bone, etc.
The need of FEA analysis would greatly influence the surgery as it would give a superior advantage in forecasting any onset of osteoporosis as done in our study in addition to other advantages specified above.
Kajzer et al. [14] in their study have indicated that maximum mass of the bone tissue is available at an age of 30 years. At this age metabolism of bone is stabilised and osteoblastic and osteoclastic processes are in equilibrium. After the age of 40 intensification of osteoblastic effects is reduced and demineralization process starts to dominate that causes loss of bone mass. They further reported that every year 0.5-1.5% minerals are lost due to demineralization process. But demineralization is more rapid in osteoporotic bone which indicates a loss of 2-5% a year according to study conducted by Nelecz [15]. During this process the osteoporitic bone is supposed to become porous and brittle.
Youngs modulus of bone changes with age as shown in Figure 5. It is related with demineralization of bone. Increase of bone porosity is caused by different factors, for example osteoporosis which is characterized by decrease of bone mass, disordered microarchitecture of bone and as a result decreased mechanical strength. These factors lead to fracture risk [14]. Knowledge of material data and mechanical properties of bone tissue (tensile, bending and torsional strength) allows evaluating stresses and strains in bones and selecting mechanical properties of implants [14-16].
Deoghare et al. [17] in his research concluded that the integration of CAD modelling, Rapid Prototyping technique (RP) and Finite Element Method are important in medical applications to reduce the complex analysis undertaken during surgeries. He had developed a 3D model from CT dicoms which was converted it into .STL format with the aid of CAD software. He did analysis on spine model considering force of 2.2 KN, Poisson’s Ratio as 0.3 and Young’s modulus as 50 Mpa, using ANSYS software. He suggested that Rapid Prototyping which is presently used to develop an actual prototype enables the medical practitioner for accurate understanding of the anatomical structure of the patient’s bone and helps him in finding out the defects which will greatly influence the planning for the surgical approach. He concluded that the integration of technologies such as Medical Imaging, CAD modeling, RP and FEM is important in medical field to reduce the cost, post operative care and risk associated with the persons undertaking a surgery. Baradeswaran et al. [18] had proposed reconstruction of images into 3D models in Medicine. They outlined the importance of reconstruction of 2D Scanned Dicom images into 3D models by using CAD packages. Physical model derived from CT or MRI data is converted into the 3D model for direct and flexible understanding of complex anatomical details that cannot be directly analyzed by using the 2D images. The precision, safety and speed of the surgery are increased, the complexity of surgery is reduced which lead to reduction in the operation time. Swetha et al. [19] had conducted research on skull Implants, she initially prepared a 3D model from CT scan of the person’s defected skull. The best suitable accurate implant was developed for the defected area with the help of simulation tool in MIMICS. The ANSYS software was used to select the model with a specific material to assign material properties such as Poisson’s ratio and Young’s modulus to the implant. After conducting the finite element analyses on Titanium, Steel and Poly Methyl Methacrylate (PMMA) implant materials at different static load conditions a suitable material was identified. She proposed that, this analysis maybe useful in future for stress and strain distribution for skull defects caused by accidents and trauma. This paper aims to outline the importance of reconstruction of images into 3D models in medicine to find out the stress distribution on the bone, the probability of a fracture and also to diagnose the condition of the femur bone. Due to this methodology, it paves the way to the doctors or surgeons to undertake a quick, accurate, confident and successful surgery.
The CT scan dicom data sets consist of two dimensional crosssectional images which were converted into three dimensional model using MIMICS software. A Computed Tomography (CT) is a medical image developer that utilizes computer processed X-rays to produce tomography images or slices of required specific areas of the body [20]. There are various software tools that are available in the market such as MIMICS, 3D Slicer, Amira, 3D doctor, Simple ware, Optimedi 3D bone extractor etc. Among these software tools MIMICS software is selected because it is having distinct features when compared with all the other tools [21]. It creates the model from dicom data sets and also generates the surface and volumetric mesh whereas the other tools do not provide this feature. Only model preparation can be carried out through them and for meshing we have to go for other software like Rhinoresurf, Geometric studio, Mesh lab etc. This process is quite complicated and increases errors while exporting and importing operations. Under these circumstances MIMICS is the best suitable software for modelling purpose. For analysis purpose the COMSOL 5.0 Multiphysics software is used. Finite element analysis (FEA) also can be carried out with different softwares like Ansys, Abaqus, Auto Desk, COMSOL, LS-Dyna, Hyper works, Deform etc. Among these tools the COMSOL is selected due to its inbuilt ’Bio-heat’ module. This module consists of default properties like thermal capacity and material property for body organs like bones, membranes etc, as the bone is subjected to heat, i.e., heat liberated from other body organs like blood vessels, mussels and soft tissues. The model is created from two dimensional images to three dimensional models for ten numbers of persons. Models are surface meshed and volume meshed using the 3-Matic module present in the MIMICS software. Then the models are exported to the COMSOL software to assign material properties to bone model, calculating the stress induced, when it subjected to static loading using the software. Table 1 defines the material properties of model. A flow chart of step by step procedure conducted is shown in Figure 6.
| S.No. | Property | Value |
|---|---|---|
| 1 | Heat capacity at constant pressure | 1313J/(kg*K) |
| 2 | Thermal conductivity | 0.32W/(m*K) |
| 3 | Density | 1.6-1.7g/cm3 |
| 4 | Young's modulus | 10–15Gpa |
| 5 | Tensile strength | 90–130Mpa |
| 6 | Compressive strength | 130–200Mpa |
| 7 | Fracture strain | 1–3% |
Table 1: Material properties of bone.
Finite element analysis of femur bones
Figure 7 shows the Finite element analysis of a person at an age of 34 years. Alexander et al. [22] had conducted FE analysis on femur bone with an applied load of 2317N, which is the maximum loading condition on femur bone for a person standing on one foot. After applying this load of 2317N the maximum stress observed to be acting on the bone was 29.7 MPa. The red color indicates the maximum stress affected region, where as pale red and yellowish colors indicates the high stresses region but comparatively less with red, where as the blue color indicates the minimum stress distribution region. The maximum stress distribution showing red color is the fracture occurring region where as the minimum stress is the safest region. Here maximum stress is not formed as fracture risk observed is very low.
Figure 8 shows the results of a person at an age of 43 years.The maximum stress occurred after applying the load is 33.2 Mpa. Here, maximum stress (red colored) is occurring at lower trochanter region. Hence, there is a chance of occurrence of fracture on lower trochanter region which is classified as subtrochanteric fracture.
Figure 9 shows the results of a person at an age of 67 years.The maximum stress occurred after applying the load is 59.9 Mpa. Here, maximum stress (red and pale yellow) is occurring at femoral head and femoral neck region. Hence, there is a chance of occurrence of fracture mostly at the upper extremity region of a femur bone. These kinds of fractures are classified as sub-capital neck fracture, transervical neck fracture and intertrochanteric fracture.
Figure 10 shows the results of a person at an age of 68 years.The maximum stress occurred after applying the load is 53.1 Mpa. Here, maximum stress (red and pale yellow) is occurring at lower trochanter region and femur shaft region. Hence, there is a chance of occurrence of fracture is mostly at these regions of a femur bone. These kinds of fractures are classified as subtrochanteric fracture.
Figure 11 shows the results of a person at an age of 84 years.The maximum stress occurred after applying the load is 65.6 Mpa. Here, maximum stress (red and Pale Yellow colored) is occurring at upper extremity regions like femoral head and femoral neck. Hence, there is a chance of occurrence of fracture is mostly at these regions of a femur bone. Finite element analysis is carried out for all the models, the vonmises stress are plotted for ten numbers of persons and are tabulated in Table 2.
| Name of the patient | Age (years) | Stress (Mpa) |
|---|---|---|
| Person 1 | 27 | 24.1 |
| Person 2 | 34 | 29.7 |
| Person 3 | 40 | 37.9 |
| Person 4 | 43 | 33.2 |
| Person 5 | 52 | 44.5 |
| Person 6 | 61 | 51.2 |
| Person 7 | 67 | 59.9 |
| Person 8 | 68 | 53.1 |
| Person 9 | 76 | 60.4 |
| Person 10 | 84 | 65.6 |
Table 2: Stress values obtained corresponding to their age.
Table 2 shows that, as the age is increases the stress values are also increases. This is due to the weakening of bone. The bone at the late age of people is not able to bear the load which is acted upon it in an axial direction. This also indicates that due to reduction of mineral content in the bones, the bone loses its density and hardness thereby becomes fragile. In this stage there is some amount of porosity in bone where the bone is prone to fracture even with less amount of application of the load. Hip fractures are becoming quite common now days due to the lack of awareness on maintaining mineral content of the body.
Comparison between stress and age
In the following Figure 12 a graph showing stress values of ten number of persons corresponding to their age group is shown. Ten numbers of persons age group is taken in horizontal direction and the vonmises stress values are taken in vertical direction in MPa units.
The above chart shows the comparison between the age group and Vonmises stress values. It can be realized from the above graph that with the increase in the age of a person, the stress values is also increasing. This is because of reduction in mineral density in bones as the age increases. From the Figure 12, the person at the age of 27 years has stress value of 51.2 N/m2 and a person at the age of 84 years is having a stress value of 65.6 N/m2. Generally, if the stress value increases then the material may fail, but where as in this case, the maximum stress defines the lack of bone mineral content per unit area. In detail explanation, stress means the force acting upon a unit area. Maximum stress occurs only with the component is having inadequate area, if the component (bone mass) have an adequate area then the stress value also reduces with respective to the area. Hence it means that bones having much area the stress values are reduced as the mineral content present in the bone is high. With the decrease in bone mineral density the stress values are increased. Stress values are inversely proportional to the mineral content in bones.
From the graph it can be further identified that the person at the age of 40 and the person at the age of 67 have more stress values compared to neighboring age groups. This is due to the fact that bones are having less mineral density at their age, i.e., the persons at the age of 40 and 64 are likely to have either weak bone or osteopenia and osteoporosis diseases. By analyzing the Figure 12, we may not judge the persons disease accurately but we can expect the fragility and fracture risk of the bone with the help of COMSOL plots. We can finally judge the diseases like osteopenia and osteoporosis only by preparing T-score values and after comparing the results with bone densitometry standards.
The above Figure 13 shows correlation between the age and stress for ten number of persons analysis results. Here, age group is taken out in horizontal axis and stress values are taken in vertical axis. In this figure, correlation between stress values and age group is noted as 0.9655 which is approximately equals to 1. These values show that, there is a linear increment of stress with respective to age. Hence we can say that stress is directly proportional to the age group which indicates as the age increases the stress acting on the also increases simultaneously.
Preparation of T-score results for analysis
NHANES standards prepared a T-score clear to define osteoporosis, osteopenia and normal bones. According to this standards the mineral density T-score should be lie in the region as follows:
• T-score of greater than minus 1 is considered normal bone.
• T-score of minus 1 to minus 2.5 is considered osteopenia bone.
• T-score of less than minus 2.5 is diagnostic of osteoporosis bone.

According to this formula, the reference young adults T-score is taken out from the NHANES standards, i.e., the person at the age of 25years of old of same gender is considered as Reference stress. Here the Reference stress obtained for 25 years old is 21.83N/m2. The standard deviation is carried out for the ten number of persons.
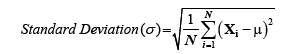
Where N=10 (Stress values of ten person like 24.1, 29.7, 37.9, 33.2, 44.5, 51.2, 59.9, 53.1, 60.4 and 65.6 N/m2). Before going to calculate standard deviation, the mean of ten persons stress should be calculated by using the formula:
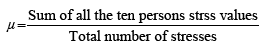
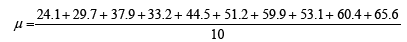
Hence, mean (μ)=45.96
After calculating mean value next have to calculate the value 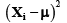
where Xi = Stress values obtained from comsol, X1=24.1, X2=29.7,.............X10=65.6.
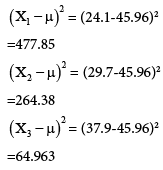
Similarly, 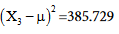
After finding all ten persons 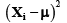 values the variance should be calculated by using the formula as follows:
values the variance should be calculated by using the formula as follows:
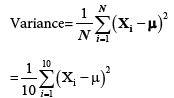
Variance=183.8971
Now, substituting this variance value in standard deviation formula:
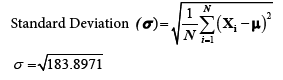
Standard Deviation(σ ) =13.5608
Sample calculations for T- Score value of a person at an age of 27 years old:
Person Stress is 24.1
Standard Deviation is 13.5608
Substituting in T-Score formula:
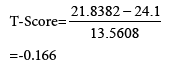
The T-score is calculated for the person of an age of 27 years old is “-0.166”.
T-scores for all the persons are calculated for ten numbers of models, both stress values and T-scores of respective age groups are tabulated in Table 3.
| Name of the patient | Age (years) | Stress (Mpa) | T-Score |
|---|---|---|---|
| Person 1 | 27 | 24.1 | -0.166 |
| Person 2 | 34 | 29.7 | -0.579 |
| Person 3 | 40 | 37.9 | -1.184 |
| Person 4 | 43 | 33.2 | -0.844 |
| Person 5 | 52 | 44.5 | -1.67 |
| Person 6 | 61 | 51.2 | -2.16 |
| Person 7 | 67 | 59.9 | -2.8 |
| Person 8 | 68 | 53.1 | -2.305 |
| Person 9 | 76 | 60.4 | -2.84 |
| Person 10 | 84 | 65.6 | -3.22 |
Table 3: T- score values of various persons corresponding to their age and stress.
Comparing results with bone densitometry standards
Figure 14 shows the graph plotted between the Age and the Tscore values to bring out comparison between ages matched T-score results with bone densitometry standards. Here, the T-score is taken in vertical axis and the age is taken out in horizontal axis.
The above graph describes the T-score according to their age group. The T-score value is reducing as the age increases. The person at the age of 27 has T-score value is -0.166 and the person at the age of 84 years have the T-score value as -3.22. According to the bone densitometry standards if the T-score value lies between +1 to -1 then bone is considered to be normal bone, If the T-score value lies between -1 to -2.5 then bone is considered as the osteopenia bone and if the T-score value less than -2.5 then the bone is considered as an osteoporosis bone.
From the above Figure 14 it can be concluded that the persons at the age of 27, 34 and 43 are having normal bone density where as the persons at the age group of 40, 52, 61 and 68 are having low bone mass density and are also are suffering with osteopenia. But the persons at the age of 61 and 68 years are experiencing severe osteopenia disease compared to 40 and 52 years of age. The persons at the age of 67, 76 and 84 are suffering severely with osteoporosis disease, which indicates high fracture risks at maximum stress affected regions.
From these above results it can be concluded that decrease in mineral density in bones occurs at the late age when the person becomes old. Instruments like DEXA may provide information only about the bone mineral density but may not give complete analysis on the bone such as maximum stress distribution region and bone fracture region. Therefore, Finite Element analysis can act as an alternate approach to determine bone mineral density in bones and determination of fracture risk and condition of the bone.
Many researchers are trying to find out a new methodology to replace the present method of identifying bone density by using dual energy x-ray absorptiometry scan. In this work, an alternate approach is proposed to find out prediction of femoral fractures, bone density and identifying normal density bone, diseased bones like osteoporosis, osteopenia. In this work, based on the T-score results of different age group models, a correlation is laid out with reference to bone densitometry standards. Scope for further extension of this present work is to convert two dimensional images generated from CT scan into three dimensional models and then to export those into ‘.stl’ file format by using CAD packages. This Model is then imported in to Rapid prototype systems; Rapid prototype technology is an additive manufacturing process that helps in producing prototype of a severely infected bone. Experimental tests like Compression test, bending test may be carried out on the produced prototype to find out the stiffness, fracture point of the bone by using universal testing machine (UTM).