Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2013) Volume 2, Issue 2
The performance diagnostic analysis of a gas turbine is accomplished by estimating a set of internal engine health parameters from available sensor measurements. No physical measuring instruments however can ever completely eliminate the presence of measurement uncertainties. Sensor measurements are often distorted by noise and bias leading to inaccurate estimation results. This paper explores the impact of measurement noise on Gas Turbine GPA analysis. The analysis is demonstrated with a test case where gas turbine performance simulation and diagnostics code TURBOMATCH is used to build a performance model of a model engine similar to Rolls-Royce Trent 500 turbofan engine, and carry out the diagnostic analysis with the presence of different levels of measurement noise. Conclusively, to improve the reliability of the diagnostic results, a statistical analysis of the data scattering caused by sensor uncertainties is made. The diagnostic tool used to deal with the statistical analysis of measurement noise impact is a model-based method utilizing a non-linear GPA.
<Keywords: Measurement uncertainty; Measurement noise; Nonlinear GPA analysis
Acronyms: BPR: By-pass ratio; CC: Combustion chamber; DP: Design Point; FC: Mass flow capacity; FF: Fuel flow rate; HP: High pressure; HPC: High pressure compressor; HPT: High pressure turbine; IE: Isentropic efficiency; IP: Intermediate pressure; IPC: Intermediate pressure compressor; IPT: Intermediate pressure turbine; LP: Low pressure; LPC: Low pressure compressor; LPT: Low pressure turbine; N: Number of measured values; OPR: Overall pressure ratio; P: Total pressure; PCN: Relative rotational speed; PR: Pressure ratio; SLS: Sea level static; T: Temperature; ΤΕΤ: Turbine entry temperature
Notations: C1: Fan/Low pressure compressor; C2: Intermediate pressure compressor; C3: High pressure compressor; T1: High pressure turbine; T2: Intermediate pressure turbine; T3: Low pressure turbine
Subscripts: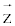 : : Dependent parameter vector;
: : Dependent parameter vector;  : : Independent (component) parameter vector; μ: Mean value; σ:Standard deviation; xi: Measured (observed) value;
: : Independent (component) parameter vector; μ: Mean value; σ:Standard deviation; xi: Measured (observed) value; 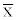 : Average measurement
: Average measurement
The main gas path components of a gas turbine engine, namely compressor and turbine, are inherently reliable. However its operation under hostile environments, such as varying conditions of load, temperature and speeds, and the cycle sensitivity to component degradation, results into engine breakdowns and performance deterioration [1-4]. The deterioration of the gas path components cannot be prevented, and the engine performance always degrades increasingly with time. In an attempt to reduce the risk of such unwanted circumstances, commercial and military gas turbine users have engaged in some form of performance diagnostics.
Gas turbine performance diagnostics is a fairly mature methodology to accurately detect, isolate and assess the changes in engine module performance, engine system malfunctions and instrumentation problems from knowledge of measured parameters taken along the engine’s gas path. Good estimates allow operators to make safe decisions, regarding the required maintenance actions. Different diagnostic approaches are adapted and developed, in order to restore the integrity and performance of the engine but one of the most popular is Gas Path Analysis (GPA), presented by Louis A. Urban [5].
GPA is a model-based mathematical technique that estimates individual modules and sensor performance shifts, from any specified set of engine measurable parameters and component characteristics, through the aero-thermodynamic relationships which exist between them [6]. The selection of sensors must be selected with great care since they will specify the level of confidence with which GPA will diagnose multiple component(s) faults. The optimal selection of instrumentation set is, therefore critical element in reducing the magnitude of prediction errors. Despite of the fact, sensors have good reputation on accurate measurements, measurement noise is inevitable, and there is a high possibility of affecting undesirably their reliability. The main reason is due to the harsh operating environment of gas turbine sensors such as high pressure and temperature, and large gradients. In many cases, the order of magnitude of the noise could be comparable to the variations in the measurements caused by an actual component fault [7].
In this research, the present of measurement noise is dealt with by processing a large number of readings and appropriate statistical techniques. The gas turbine diagnostic program used for this study is Gas Path Analysis (GPA) technique [8] developed at Cranfield University. The GPA has been applied to a gas turbine model engine, a civil high by-pass ratio turbofan engine, similar to Trent 500 manufactured by Rolls Royce plc. Non-linear GPA is the diagnostic tool that prefers to be used in this research because proved to take a significant advantage on the severe limitations of linear GPA models since it addresses the nonlinear nature of the engine thermodynamic behavior.
Gas path analysis
Gas Path Analysis (GPA), pioneered by Urban [9-11] is used to assess the condition of individual engine components, based on the aero-thermodynamic relationships that exist between the component and direct measurements of gas path parameters [12]. The theory behind this relationship can be summarized by: “The presence of a primary gas-path physical fault induces change in the component characteristic that shows up a deviation of the measurable parameters from the baseline conditions” [13]. Therefore, the purpose of the GPA is to detect, isolate and quantify the gas path components faults that have observable impacts on the measurable variables with the hope that will facilitate the subsequent isolation of the underlying physical fault. For a gas turbine engine, the mathematical relationship between dependent (engine component health parameters) and independent parameters (gas path measurements) is expressed analytically as [13,14]
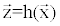 (1)
(1)
The assumption of linearity becomes increasingly false, when deteriorations cause the engine to operate further away from the condition for which the matrix was calculated [1]. Therefore, a nonlinear GPA diagnostic technique is preferred instead of the linear technique at the present paper, due to the consideration of the nonlinear nature of the engine thermodynamic behavior [1,10]. The nonlinear GPA uses the Newton-Raphson iterative technique, where the linear GPA prediction process is applied iteratively until a converged solution is obtained [8].
Measurement uncertainty
The purpose of measurements is to numerically characterize the performance and condition of a gas turbine. Properly understanding of the data obtained from such measurements, is crucial to applying the knowledge thereby gained. It is important to note that, errors and flaws in measurements are always present and should never be stated with complete exactness. Real measuring indications can only be assumed to be made under perfect conditions; no measurement elaborate or precise or how often repeated, can ever completely eliminate any kind of uncertainty. A brief and generic definition of the measurement error is described in [15] as the amount by which a measured value differs from the true value. Therefore, the presence of uncertainties in measurements should be recognized as the starting point in a discussion of errors [16].
Measurement noise
In GPA diagnostic analysis of gas turbine engines, measurement noise exists in any measurement and its impact has to be taken into account as the measurement noise may affects the accuracy of GPA diagnostic results. Measurement noise in gas turbine measurements is a term to describe the value of measurement parameter centered on its average value; representing a band within which the true value of the measurement parameter is expected to lie [17]. Therefore, the values of the gas path parameters taken from the gas path measurement can only be seen as an approximation of the true values of those parameters. Suppose that the measurement noise distribution is of Gaussian type, the distribution of the measurement of a gas path parameter would be that shown in figure 1.
The accuracy of the measurements is determined by the standard deviation σ, supposing measurements are bias-free. The term standard deviation is used in quantifying measurement precision. The precision error is determined by taking N repeated measurements from the parameters of which can be approximated by the precision index and can be estimated as
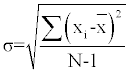 (2)
(2)
Since the Gaussian or Normal distribution is a symmetric distribution, it has the property that a known percentage of all possible values of x lie within a certain number of standard deviation σ of the mean value. For example, around 68% of normally distributed observed samples lie within the interval (μ ± 1σ), 96% within (μ ± 2σ), and 99.7% within (μ ± 3σ), as shown in Figure 1. Consequently, a large value of σ means that there is a lot of scattering in the measurements and a small value of σ reflects relatively less scatter.
Analysis procedure of noise impact
Besides measurement noise, other problems related measurement quality can be detected and derive from:
• Sensor accuracy, i.e. measurement bias.
• Uncertainties not directly related to measurements, but to ambient condition and gas turbine operating conditions.
In this research all the above uncertainties are assumed not exist and only measurement noise is being considered. The proposed methodology in analyzing the impact of measurement noise on gas turbine GPA diagnostics is divided into the following main steps:
• A model engine performance model is created with thermodynamic performance software and therefore all the true value of gas path measurements can be simulated.
• One set of gas path measurements were selected. Gas path measurements of the model engine at different engine health conditions were simulated.
• A large number of measurement samples with random measurement noise are simulated by superimposing the simulated measurements with different level of measurement noise.
•The simulated measurement samples are used as input to the GPA diagnostic system to predict engine degradation.
• A statistical analysis of the predicted engine degradation with large number of measurement samples is carried out and the impact of measurement noise on the degradation prediction is analyzed.
Model engine
The engine model selected for the noise impact analysis in this research is similar to Rolls Royce Trent 500, a three spool, highbypass turbofan engine rated in 249 kN net thrust at sea level. In figure 2 there is a schematic representation of the model engine. The model engine was simulated using TURBOMATCH, a FORTRANbased gas turbine simulator developed at Cranfield University [18]. Normally, it is appropriate to define DP of a gas turbine in cruise conditions because the aircraft spend most of the operational time at this situation. However, in the current research the DP was chosen at the take-off condition because the available open access databases for the performance parameters of this engine refer to the ground testing [19]. Therefore, the performance specifications of the engine at the DP are presented under the atmospheric conditions of SLS.
| Performance Parameter | Value | |
|---|---|---|
| Ambient Temperature | (K) | 288 |
| Inlet Mass Flow Rate | (kg/s) | 879.5 |
| BPR | (non-d) | 7.5 |
| TET | (K) | 1600 |
| Net Thrust | (kN) | 249 |
| LP Compressor / Fan PR | (non-d) | 1.5 |
| IP Compressor PR | (non-d) | 5.9 |
| HP Compressor PR | (non-d) | 4.1 |
| OPR | (non-d) | 36.3 |
Instrumentation set selection
The success of any fault diagnosis technique depends critically on the sensor network, measuring the important observed parameters. An optimally designed sensor network for fault diagnosis should observe all the faults when they occur, and also distinguish between them to the maximum extent possible [20]. Therefore, the instrumentation set should be properly chosen for better detection of engine degradation because the quality of the diagnostic analysis relies on the quality of the measurements. Table 1 shows all the potential gas path measurements for the model engine and table 2 all the health parameters of potential degraded engine components. For the measurement set to be effective in the GPA diagnostic analysis, the chosen measurements should be sensitive to engine degradation and independent from each other. To assist the selection of measurements, a sensitivity analysis is carried out, where the response of all the potential gas path measurements, due to unit deviation of each of the engine component health parameters, are obtained, by using performance simulation of the model engine.
| Symbol | Measurement Parameters | Unit |
|---|---|---|
| PCN1 | C1 relative rotational speed | % |
| PCN2 | C2 relative rotational speed | % |
| PCN3 | C3 relative rotational speed | % |
| P3 | C1 exit total pressure | atm |
| T3 | C1 exit temperature | K |
| P5 | C2 exit total pressure | atm |
| T5 | C2 exit temperature | K |
| P7 | C3 exit total pressure | atm |
| T7 | C2 exit temperature | K |
| P10 FF |
CC exit total pressure Fuel flow rate |
atm kg/s |
| P14 | T1 exit total pressure | atm |
| T14 | T1 exit temperature | K |
| P16 | T2 exit total pressure | atm |
| T16 | T2 exit temperature | K |
| P17 | T3 exit total pressure | atm |
| T17 | T3 exit temperature | K |
Table 1: Potential Gas Path Measurements.
Figure 3 illustrates the plotted sensitivity of all potential gas path measurements against all the model engine health parameters and the number of faults taken from table 2. Based on the sensitivity of the measurements, a set of six measurement parameters is then selected for the diagnostic analysis of the model engine. The selected measurement set is:
| Fault No. | Meaning | Health Parameter |
|---|---|---|
| 1 | C1 isentropic efficiency | IEC1 |
| 2 | C1 flow capacity | FCC1 |
| 3 | C2 isentropic efficiency | IEC2 |
| 4 | C2 flow capacity | FCC2 |
| 5 | C3 isentropic efficiency | IEC3 |
| 6 | C3 flow capacity | FCC3 |
| 7 | T1 isentropic efficiency | IET1 |
| 8 | T1 flow capacity | FCT1 |
| 9 | T2 isentropic efficiency | IET2 |
| 10 | T2 flow capacity | FCT2 |
| 11 | T3 isentropic efficiency | IET3 |
| 12 | T3 flow capacity | FCT3 |
Table 2: Health Parameters of potential degraded engine components.
Total pressure at the exit of IP and HP compressor (P5, P7)
Total pressure at the exit of HP and IP turbine (P14, P16)
LP and HP spool rotational speed (PCN1, PCN3)
In an attempt to investigate the impact of measurement noise on performance diagnostics, engine component degradation is implemented into the model engine using TURBOMATCH software and gas path measurements are simulated. The implemented degradation is assumed unknown to the engine users and simulated measurements are used to predict the seeded fault. As the linear GPA is less effectively compared with its non-linear partner only the nonlinear GPA technique is used in diagnostic analysis. Figure 4 presents in the form of histograms the differences of performance parameters with noisy and noise-free measurements. The example used to study the influence of measurement noise was an implemented fault of 2 percent drop in flow capacity and 2 percent loss in isentropic efficiency, in both compressor and turbine of the engine. The accuracy of the non-linear GPA predictions with the influence of nominal noise level is about 0.2 percent in average except FC at IP compressor where its prediction error is over 0.8 percent. However, the noisy measurements do not seem to result in large prediction errors in the diagnosis of the examined degradation. Certainly, the impact of measurement noise on performance diagnostics is negative but it can consider being small and acceptable.
Measurement sample set selection
The impact of measurement noise was investigated by using selected set of measurements with a large number of samples and different levels of measurement noise. The problem arises is the number of samples that should be chosen to get meaningful statistic analysis results. After applying the non-linear GPA to the model engine with a varying sample sizes (500 to 5000 samples), a fixed sample size is selected. Table 3 lists the optimum (minimum) measurement sets for each fault case, under the condition that the distribution of the health parameter on the selected set satisfies the Gaussian distribution conditions. The largest number of samples found to be 4000.
| Number of Measurement Samples | |||||||
|---|---|---|---|---|---|---|---|
| Compressor | Turbine | ||||||
| LP/Fan | IP | HP | HP | IP | LP | ||
| Health Parameter | FC | 3000 | 1500 | 4000 | 1500 | 2500 | 3000 |
| IE | 2000 | 500 | 4000 | 2000 | 3000 | 500 | |
Table 3: Number of optimum samples for each component fault case.
Statistical analysis of measurement noise impact
The difference between the predicted mean degradation and actual degradation in percentage indicates the accuracy of diagnostics. Tables 4 and 5, show the impact of measurement noise on the prediction accuracy of the model-based diagnosis of the gas turbine engine. For example, the standard deviation (2σ) in table 4 of the predicted C2 and T3 degradation are 2.1 and 1.8 percent. When noise level drops down to one third (2σ/3) the standard deviations seem to fall also down to 0.8 percent for both components. The same changes happen when measurement noise rises by i.e. three times (3x2σ) and the standard deviations for the same components as mentioned before increase by 3.8 and 4 percent respectively. Similarly, in the case of isentropic efficiency drop presented in table 5, the standard deviation of the predicted degradation changes proportionally with the noise levels. Figures 5 and 6 plot results of table 4 and 5 respectively on graphs to demonstrate the impact of different level of measurement noise on the prediction accuracy of engine component diagnostic analysis.
| % | Standard Deviation % | |||||
|---|---|---|---|---|---|---|
| Noise Level | C1 | C2 | C3 | T1 | T2 | T3 |
| 2σ / 3 | 0.3 | 0.8 | 0.3 | 0.1 | 0.2 | 0.8 |
| 2σ / 2 | 0.4 | 1.1 | 0.5 | 0.2 | 0.3 | 1.0 |
| Std Dev. or 2σ | 0.8 | 2.1 | 1.0 | 0.4 | 0.6 | 1.8 |
| 2 x 2σ | 1.6 | 4.0 | 1.9 | 1.0 | 1.4 | 3.8 |
| 3 x 2σ | 2.4 | 5.9 | 2.9 | 1.5 | 1.9 | 5.8 |
Table 4: Impact of measurement noise on flow capacity degradation predictions.
| % | Standard Deviation % | |||||
|---|---|---|---|---|---|---|
| Noise Level | C1 | C2 | C3 | T1 | T2 | T3 |
| 2σ / 3 | 0.4 | 0.1 | 0.1 | 0.2 | 0.3 | 0.6 |
| 2σ / 2 | 0.5 | 0.2 | 0.2 | 0.3 | 0.4 | 0.9 |
| Std Dev.or 2σ | 1.0 | 0.3 | 0.3 | 0.6 | 0.9 | 1.6 |
| 2x 2σ | 1.9 | 0.7 | 0.9 | 1.8 | 1.9 | 3.6 |
| 3 x 2σ | 2.9 | 1.0 | 1.3 | 2.8 | 2.6 | 5.5 |
Table 5: Impact of measurement noise on isentropic efficiency degradation predictions.
The results also explain why the Gaussian distribution tends to be flatter as the measurement noise increases, making the scatter range wider. Flatter distributions lessen the possibility for an arbitrary measurement to be highly precise to the expected value, because the scatter around the average increases the precision error, which specifies the characteristics of measurement in greater detail. As precision refers to the level of measurement and exactness of description in the range of measurement uncertainty, the precision error increases the loss of information. More precise measurements have smaller uncertainties, therefore the negative impact of large standard deviations and measurement noise is the difficulty for any user to evaluate the condition of the engine, because the data from high distributions can mislead the diagnostic process due to high precision error.
The impact of measurement noise on engine component fault diagnosis was achieved in this paper. The impact of noisy measurements on the gas path components parameters analyzed and quantified where the measurement noise is assumed to exhibit Gaussian distribution. The statistical analysis shows that the variation of measurement noise levels has obvious impact on the prediction accuracy of the non-linear GPA gas path diagnostics and every measure should be taken to reduce the level of measurement noise in order to improve the accuracy of the diagnostic results.