Journal of Oceanography and Marine Research
Open Access

The Immortal Science of Dead Water: Effects of Internal Wave Drag on Propagating Submerged Bodies

Marco Danieletto, Justin M Brown^* and Timour Radko ^*Correspondence: Justin M Brown, Naval Postgraduate School, 1 University Circle, Monterey, CA 93943, USA, Tel: 18312520921, Email:

Author info »

Introduction

Accurate predictions of drag are integral to maximizing the efficiency of vehicles in a number of transport sectors, including those pertaining to nautical and aeronautical systems. Calculating the amount of drag on a vessel determines how much fuel is required and how long it will take to complete a voyage. In military circumstance, the amount of drag on a body is intrinsically tied to the presence of detectable signatures in the wake and hence minimizing drag is tantamount to lowering the risk of detection. A large amount of the research on drag for such bodies focuses on the effects of hydrodynamical shapes, but the environment can also play a large role, which has important consequences for shipping routes in regions with strong stratification, such as is generated by river runoff between the Kara and Chukchi Seas. It is therefore important for the purposes of calculating optimal routes for trading, military, and research vessels to know the precise impact of the surrounding water on the vessel in order to minimize drag and therefore maximize efficiency. While a few select studies have investigated the impact of the drag caused by the stratification of the environment, the subject of comparing its effects on surface and submerged vessels has not yet been addressed. This subject is of great import to the efficiency of underwater vehicles that can elect to traverse the ocean at various depth levels and may require guidance with regard to their optimal operation.

We consider here the effects of stratified flows on drag for surface vehicles and submersibles. For a general discussion of the production of wakes by such bodies, the review by Townsend [1] is an old but useful reference, and Spedding [2] provided a more recent discussion of stratified wakes. The broad study of towed bodies in stratified fluids has resulted in a large body of collective work spanning methodologies from analytics and numerics [3-8] to laboratory experiments [9-14].

One source of drag in stratified systems is the so-called “dead-water” phenomenon, which was first discovered north of Siberia, near the Nordenskiöld islands by Nansen [15], while sailing on board the Fram on calm seas in 1893. Nansen experienced a severe and inexplicable decrease of velocity, resulting in the loss of steering power [15]. This process has received only limited attention in the literature of stratified wakes since Ekman provided the initial laboratory study of the subject [16]. Dûchene renewed this study with an asymptotic analysis of a two-layer system with a surface vessel and Mercier, Vasseur, and Dauxois extended the laboratory studies with three-layer and linear stratification [17,18]. Grue since found numerically that linear models of this system are inadequate to reproduce the results of two-layer experiments, such as those by Lacaze et al. and that non-linear models are required [19,20].

On the other hand, a great deal of attention in the literature has focused on drag effects of submerged bodies in a stratified fluid. Some of the first experiments were performed by Schooley and Stewart [13], who found that stratified wakes begin to collapse after a buoyancy period and generate internal waves. In this literature, the topic of “dead water” is instead referred to as “lee-wave resonance,” which was explored experimentally for a submerged sphere by Lofquist and Purtell [21], who discovered that this stratified drag effect depended strongly on the ratio of the body velocity to the maximum phase speed of the system. Additional studies by Hopfinger et al. [14] and Bonneton et al. [22] began to categorize wake structure in terms of turbulence, finding that the lee waves responsible for the increased drag effect were more prevalent for slower moving bodies. Though most of these studies have been for spherical bodies, Meunier and Spedding [10] concluded through a series of numerical experiments that the shape of the body has only a small effect on the wake through a parameter they term the “effective diameter” of the body. Meunier et al. [11] provided a detailed comparison of numerical and laboratory experiments, highlighting the effects of lee-wave resonance, which they prove is intrinsically tied to the increased drag.

It is important to note that while lee-wave resonance is clearly a portion of the drag caused in the stratified flows, additional drag is evident in the production of turbulence and internal waves. For the dead-water regime, the body is typically travelling slowly such that injection of turbulence is minimal [14]; however, internal waves are quite prevalent in both the surface [18,23] and submerged cases [11,13,24]. This was studied analytically by Motygin and Kuznetsov and by Radko for the surface case [23,25]. Brandt and Rottier managed to experimentally measure the total energy in the internal wave field for a submerged body [9]. In the following discussion, we will use the term “dead water” to refer to all increases in drag caused by stratification, which includes both the effects of lee-wave resonance and internal wave generation.

The aim of this work is to compare the effect of the dead-water phenomenon for submerged and surface vessels by using laboratory experiments of a towed body traveling through stratified and unstratified water. To compare the effects, we use the coefficient of drag as our primary diagnostic and that the effects on this coefficient are comparable for the two cases. The material is organized as follows. Section 2 discusses the experimental setup, and Section 3 presents the corresponding laboratory results. Afterwards, a comprehensive description and comparison of all components of this project are given in Section 4. Finally, conclusions and suggestions for future work are presented in Section 5.

Methodology

Dead water represents the dramatic increase in the form drag of a moving body associated with the radiation of internal waves, as shown experimentally by Hopfiger et al. [14]. It is commonly assumed that for this process to occur, the body must be traveling through a stratified fluid at a rate slower than the speed of internal wave propagation [19], so this phenomenon is most prevalent in strongly stratified regions such as areas where glacier runoff flows into salty water.

This condition can be described using the Froude number (Fr), which compares inertial and

buoyancy forces:

(1)

Where U is the velocity of the body, N is the Brunt-Väisälä frequency, and D is the diameter of the object. This quantity adequately approximates the ratio of the boat speed U to the maximum internal wave phase speed [17]. When the Froude number is greater than unity, radiated internal waves are slower than the body and do not significantly affect its motion (although the radiation of internal waves still results in energy loss and therefore drag). Conversely, when the Froude number is less than unity, lee waves in the wake trail stationary in the frame of the object, which results in a large drag force, which Ekman [16] considered to be the dead-water phenomenon.

Miloh, Tulin and Zilman [7] and Motygin and Kuznetsov [25] further demonstrated that the drag associated with dead-water is maximal when the Froude number is slightly less than unity, i.e., the subcritical regime. The Froude number, however, is only one characteristic that determines the wake properties: the extent of disorganization of the wake and the level of turbulence are most succinctly described in terms of the Reynolds number,Re ≡UL /ν , a measure of the relative strength of inertial and viscous effects, where U is the relative velocity of the target in the fluid, L is the size of the target, and is the kinematic viscosity of the fluid.

In order to isolate the effects of dead water, two experimental setups are used: homogeneous and stratified. By comparing the speed of a body towed with constant force between the two configurations, we will be able to quantify the dead-water drag. For the homogeneous fluid, the primary experimental tank (45 cm tall by 60 cm wide and 180 cm long) was filled with tap water with a constant, uniform temperature of 20◦C and a corresponding density of 997 kg/m³. The stratified fluid was established using the system shown in Figure 1. The primary tank was filled halfway with tap water, and the remaining water was siphoned into an auxiliary tank where it was mixed with salt and ice until its density reached 1,015 kg/ m³. The contents of the auxiliary tank were then pumped into the bottom of the primary tank via the use of a low-turbulence diffuser. Prior to each set of experiments, we used an RBR Concerto sensor to measure depth, temperature, salinity, and density anomaly with a sample frequency of 32 Hertz (Hz). The measurements of the altimeter in the sensor were calibrated linearly to the surface of the fluid and the tank bottom.

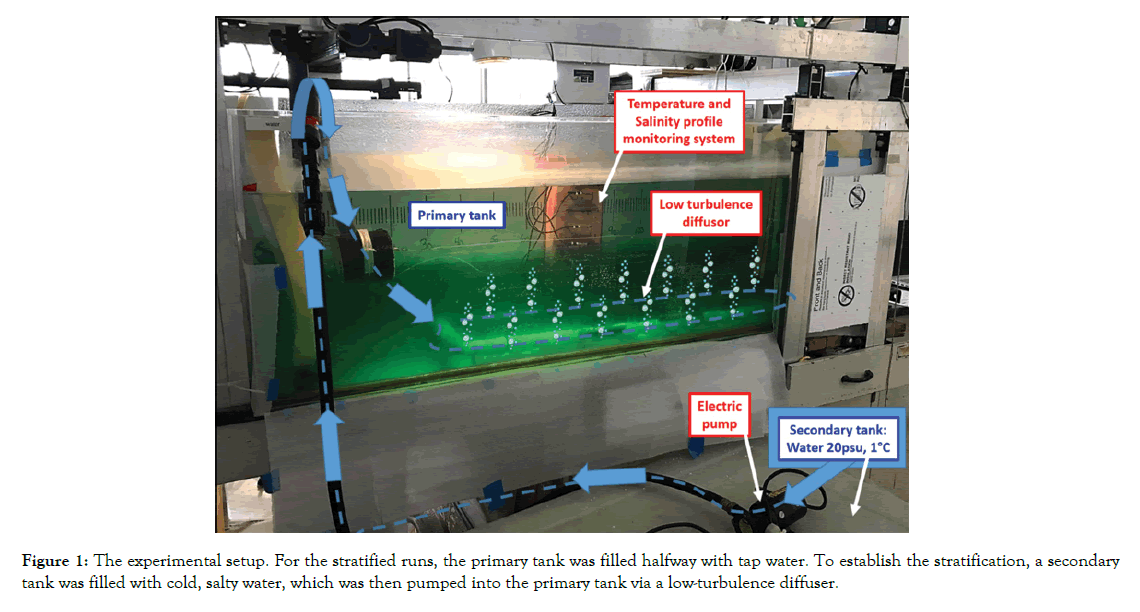
Figure 1. Surgical training questionnaire

For these experiments, a cylindrical body 12 cm in length and 13 cm in diameter was towed with a low-elasticity fishing line in the setup shown in Figures 2 and 3. The experimental framework of the pulley system reduces the effective experimental length to 130 cm. A weight of mass m was connected to the tow line, resulting in a towing force of mg, where g is the acceleration due to gravity. The system can be run in two configurations: one with the body constrained to travel along the surface (Figure 2) and one along the centerline of the tank (Figure 3). To ensure that the results are not contaminated by residual motions of previous experiments, foam was placed on either end of the tank to absorb internal waves and the system was left to relax for several minutes in between runs.

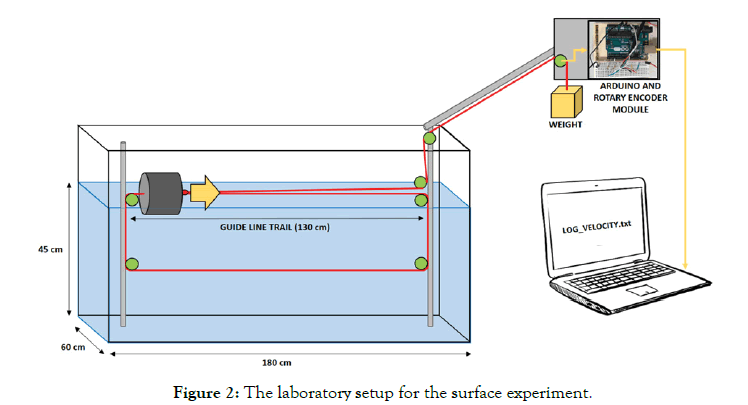
Figure 2. The laboratory setup for the surface experiment.

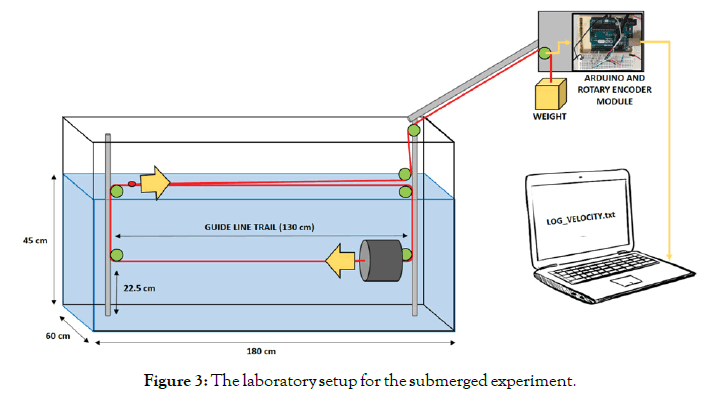
Figure 3. The laboratory setup for the submerged experiment.

A total of 16 lab experiments were performed during this project. For both the submersible and the surface cases, four runs were conducted in a stratified fluid with varying towing weights, and four runs were conducted in a homogeneous fluid with the same set of towing weights as the stratified cases. For the surface case, the towing weights were 35, 38, 40, and 42 g, and for the submerged case, the towing weights were 27, 30, 34, and 38 g. The weights were chosen to result in roughly comparable final speeds between the two systems.

Experimental Results

The experiments eventually achieved a steady state where the driving force of a body equaled the total drag force. In these experiments, this relation is expressed as follows:

(2)

where F_w is the towing weight force, D is the total drag force acting on the body, and F_l is the friction caused by the lab setup, which is assumed to depend only on the body velocity. The mean velocity during the steady state (v_h and v_s for the homogeneous and stratified cases, respectively) is used to compare complementary experiments from the stratified and homogeneous cases. The difference in mean velocity between such cases is significantly larger for the stratified water case when the dead-water phenomenon is active.

The velocity time series for the four laboratory setups are presented in Figure 4, from which it is clear that for the same values of F_w , stratified experiments have slower velocities. This behavior is consistent between the submerged and surface cases. This results from two major effects: (1) the submerged body experiences drag due to energy loss by the production of transient internal waves, such as those described by Brandt and Rottier [9], and (2) the submerged body experiences drag associated with lee wave resonance. The latter effect is only possible for those experiments where the mean velocity is less than the maximum phase speed of internal waves, which can be calculated from solving the internal wave equation, which is as follows:

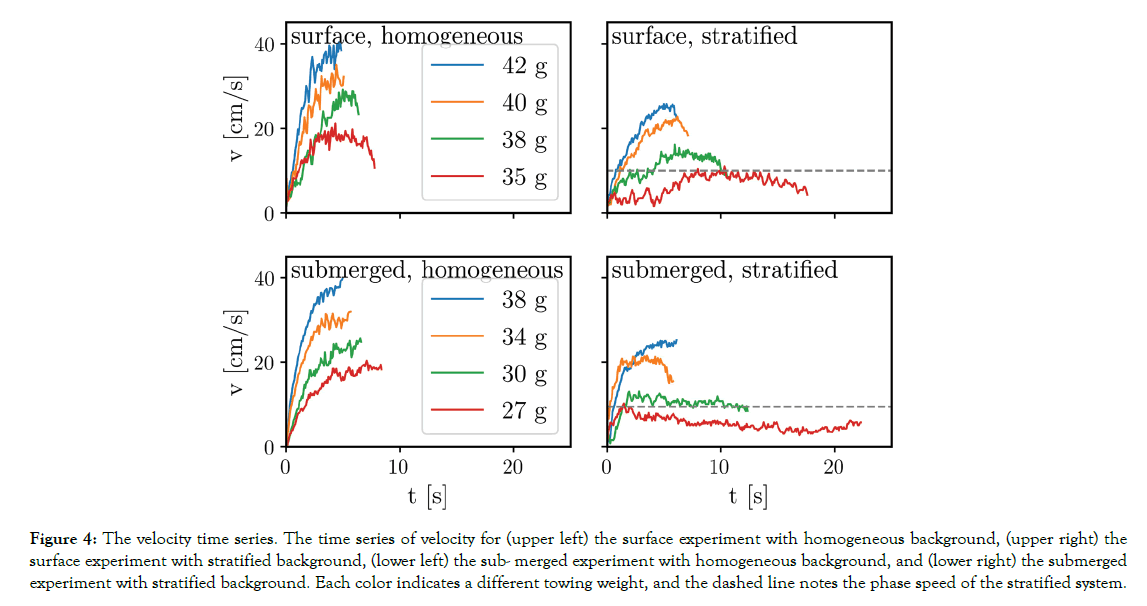
Figure 4. The velocity time series. The time series of velocity for (upper left) the surface experiment with homogeneous background, (upper right) the surface experiment with stratified background, (lower left) the sub- merged experiment with homogeneous background, and (lower right) the submerged experiment with stratified background. Each color indicates a different towing weight, and the dashed line notes the phase speed of the stratified system.

(3)

where is measured directly from the experiments and is shown in Figure 5, and w is the vertical velocity of the fluid. Solutions are sought of the form , where ω is the angular frequency of oscillation, k_x is the wave number in the x -direction, and k_y is the wave number in the y -direction. The vertical boundaries are assumed to be rigid and impermeable. We can choose our horizontal axes such that the x -direction is in the direction of the wave propagation without loss of generality. Thus, the phase speed is given by . We use finite differencing to construct an eigenvalue equation with ω² as the eigenvalue and solve for the value of k_x that results in the greatest phase speed. For our experimental stratification, this results in a phase speed of v_p =10.0cm/ s for the surface case and v_p = 9.4cm/ s for the submersible case.

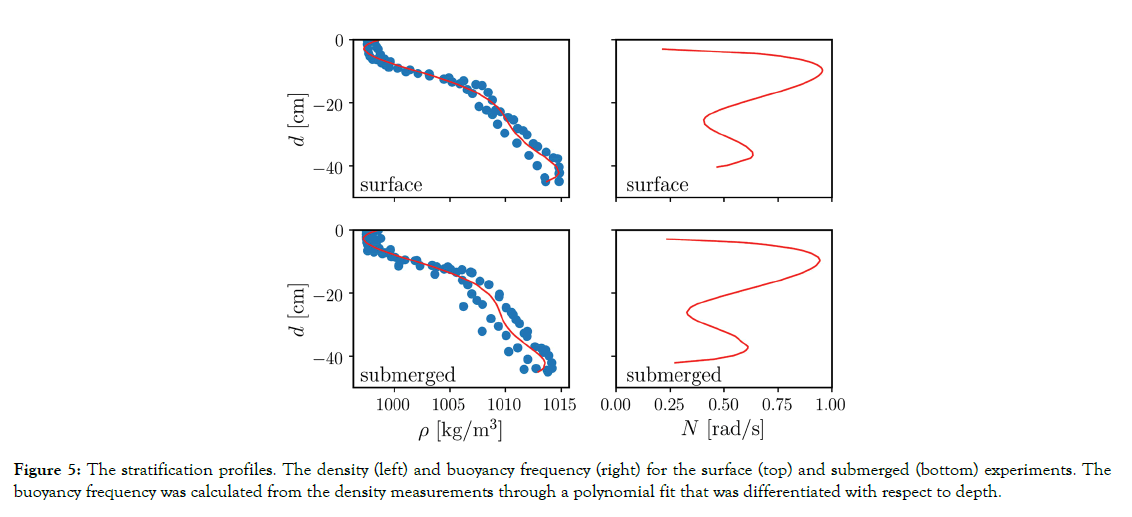
Figure 5. The stratification profiles. The density (left) and buoyancy frequency (right) for the surface (top) and submerged (bottom) experiments. The buoyancy frequency was calculated from the density measurements through a polynomial fit that was differentiated with respect to depth.

Discussion

We quantify our results in terms of the drag coefficient, C_D . This quantity is a measure of the effects of all sources of drag on a body for a given velocity and stratification, defined as

(4)

where A is the wetted cross-sectional area of the cylinder and v is the velocity of the body. The impact of the stratification is measured in this study as it was by Lofquist and Purtell [21] and Greenslade [26], though their results are for a spherical body. They present as their primary diagnostic, which we adopt here. The drag of our laboratory system must also be considered, resulting in a modified drag coefficient:

(5)

However, for the same Reynolds number, body geometry, and mean fluid density, this error term is identical, so we may equivalently write . Both the raw value of C′_D and the stratified water contribution ΔC_D are shown in Figure 6, where the unstratified modified drag coefficient for a given Reynolds number is estimated by fitting the unstratified results with a quadratic in log–log space. The contributions to the drag coefficient for the submerged and surface bodies appear comparable. It is immediately apparent that the qualitative results are similar to the experiments of Lofquist and Purtell [21] and the analytical results of Greenslade [26] for low Froude number, despite the exchange of a cylindrical bluff body for their spherical one. Both sets of experiment show a large increase in the drag coefficient below a Froude number of unity, for which the speed of the body exceeds the maximum phase speed of the system. The major difference appears in the high Froude number regime, where Lofquist and Purtell [21] measure a negative contribution to ΔC_D instead of the positive contribution measured here, though the contribution from the stratification is weak for in both. Thus, the cylindrical body does appear to generate substantially larger drag than its spherical counterpart.

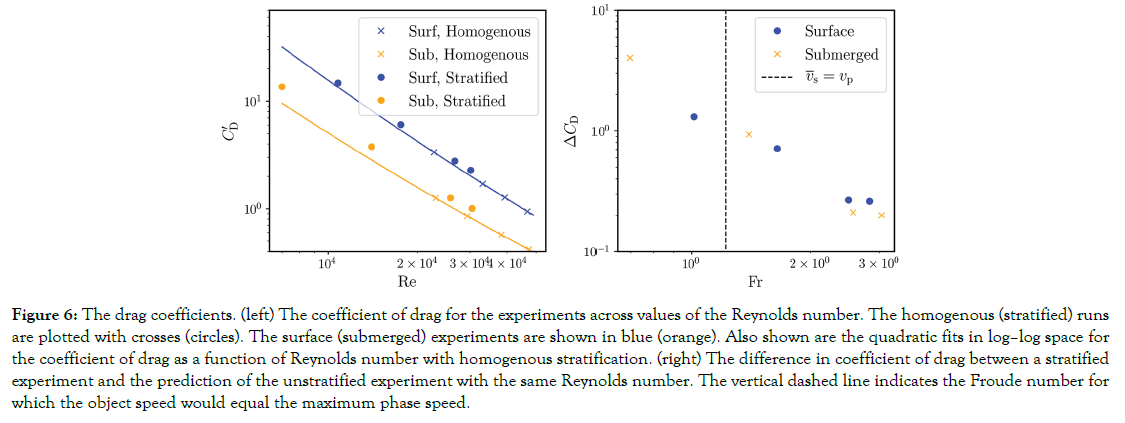
Figure 6.The drag coefficients. (left) The coefficient of drag for the experiments across values of the Reynolds number. The homogenous (stratified) runs are plotted with crosses (circles). The surface (submerged) experiments are shown in blue (orange). Also shown are the quadratic fits in log–log space for the coefficient of drag as a function of Reynolds number with homogenous stratification. (right) The difference in coefficient of drag between a stratified experiment and the prediction of the unstratified experiment with the same Reynolds number. The vertical dashed line indicates the Froude number for which the object speed would equal the maximum phase speed.

It’s interesting to note in Figure 6 that the base coefficient of drag is nearly a factor of three higher for the surface case as compared to the submerged case. This is largely due to the production of surface waves and the reduced wetted area of the body. However, given the differences in geometry between the surface and submerged problems, it is somewhat surprising that the impact on ΔC_D is minimal. This result suggests that the production of the dead-water phenomenon is largely independent of any surface phenomena and is determined largely by the bulk of the water column. However, because of the higher drag coefficient for the surface case, the submerged case sees a much larger fractional effect of dead water; that is, for a surface body and submerged body traversing through the same region, the submerged body will see a greater percentage increase in total drag force.

For an alternate method of conceptualizing the effect of stratification on the drag of the towed body, we introduce a new parameter, , which is defined as the ratio between the equilibrium velocity for the stratified and unstratified experiments: (6)

This quantity is plotted in Figure 7, where it is seen to increase with increasing Froude number, suggesting that the effects of stratification on drag become less prominent as the object velocity increases and turbulence becomes more relevant. This quantity never reaches unity for these experiments, which implies that the effects of stratification are relevant even when the object velocity exceeds the phase speed of the system. Additionally, the effects on surface and submerged bodies are comparable for high Froude number but diverge when the speed is less than the phase speed of the system. In this regime, the submerged body sees a larger impact of stratification, which is due to the aforementioned increased fractional effect of dead water for submerged bodies.

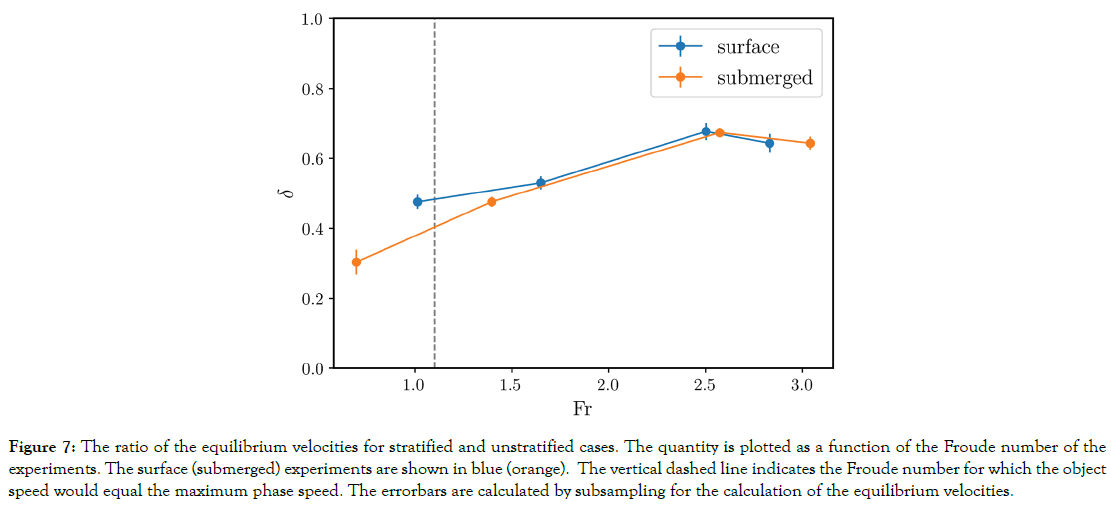
Figure 7. The ratio of the equilibrium velocities for stratified and unstratified cases. The quantity is plotted as a function of the Froude number of the experiments. The surface (submerged) experiments are shown in blue (orange). The vertical dashed line indicates the Froude number for which the object speed would equal the maximum phase speed. The errorbars are calculated by subsampling for the calculation of the equilibrium velocities.

Conclusions

We have performed a series of laboratory experiments towing a cylindrical body through a tank of water. For these experiments, we varied the depth of the body (either holding it at the surface or submerging it completely), the stratification of the tank, and the total force accelerating the body. Because the body eventually reached an equilibrium velocity, we were able to calculate the drag force on the object as a function of this velocity, which we used to construct the drag coefficient for stratified and unstratified drag on this body. By taking the difference, we were able to isolate the effects on drag caused by stratification, i.e., the dead-water phenomenon.

The major finding of this study is that dead water has a comparable effect on the drag coefficients of submerged and semi-submerged bodies. These experiments have shown clear features associated with dead water, including increased drag for experiments towed below the maximum phase speed of the medium. Furthermore, these experiments revealed larger drag for the stratified case even for speeds well above the conventional dead-water regime, likely due to energy loss associated with the radiation of transient internal waves. If confirmed by field observations, this feature could be significant for open-water shipping vessels, which have typical Arctic routes passing through regions that are strongly stratified due to river runoff, such as the waters between Kara Sea and Chukchi Sea, which extends over 1,900 nautical miles. Thus, understanding the effects of dead water remains an important topic of study for both academic and economic purposes.

Acknowledgements

This work was supported by the Naval Research Program of the Naval Postgraduate School (No. NPS-19-N155-A). This research was performed while one of the authors held an NRC Research Associateship award at the Naval Postgraduate School.

References

1. Townsend AA. The structure of turbulent shear flow. 2nd Edn. Cambridge and New York: Cambridge University Press 1956.
2. Spedding GR. Wake Signature Detection. Annu Rev Fluid Mech. 2014;46(1):273-302.
3. Augier P, Chomaz JM, Billant P. Spectral analysis of the transition to turbulence from a dipole in stratified fluid. J Fluid Mech. 2012;713:86-108.
4. Brucker KA, Sarkar S. A comparative study of self-propelled and towed wakes in a stratified fluid. J Fluid Mech. 2010;652:373-404.
5. Diamessis PJ, Spedding GR, Domaradzki JA. Similarity scaling and vorticity structure in high-Reynolds-number stably stratified turbulent wakes. J Fluid Mech. 2011;671:52-95.
6. Gourlay MJ, Arendt SC, Fritts DC, Werne J. Numerical modeling of initially turbulent wakes with net momentum. Phys Fluids. 2001;13(1):3783-3802.
7. Miloh T, Tulin MP, Zilman G. Dead-Water Effects of a Ship Moving in Stratified Seas. J Offshore Mech Arctic Eng. 1993;115(2):105-110.
8. Afanasyev YD. Wakes behind towed and self-propelled bodies: Asymptotic theory. Phys Fluids. 2004;16(8):3235-3238.
9. Brandt A, Rottier JR. The internal wavefield generated by a towed sphere at low Froude number. J Fluid Mech. 2015;769:103-129.
10. Meunier P, Spedding GR. A loss of memory in stratified momentum wakes. Phys Fluids. 2004;16(2):298-305.
11. Meunier P, Le Dizès S, Redekopp L, Spedding GR. Internal waves generated by a stratified wake: experiment and theory. J Fluid Mech. 2018;846:752-788.
12. Lin Q, Lindberg WR, Boyer DL, Fernando HJS. Stratified flow past a sphere. J Fluid Mech. 1992;240:315-354.
13. Schooley AH, Stewart RW. Experiments with a self-propelled body submerged in a fluid with a vertical density gradient. J Fluid Mech. 1963;15(01):83-96.
14. Hopfinger EJ, Flór JB, Chomaz JM, Bonneton P. Internal waves generated by a moving sphere and its wake in a stratified fluid. Exp Fluids. 1991;11(4):255-261.
15. Nansen F. Farthest North: The epic adventure of a visionary explorer. New York: Skyhorse Publishing; 1897.
16. Ekman VW. On dead water. The Norwegian North Polar Expedition Scientific Results. Christiania, Norway; 1906.
17. Duchêne V. Asymptotic models for the generation of internal waves by a moving ship, and the dead-water phenomenon. Nonlinearity. 2011;24(8):2281-323.
18. Mercier MJ, Vasseur R, Dauxois T. Resurrecting dead-water phenomenon. Nonlin Processes Geophys. 2011;18(2):193-208.
19. Grue J. Nonlinear dead water resistance at subcritical speed. Phys Fluids. 2015;27(8):082103.
20. Lacaze L, Paci A, Cid E, Cazin S, Eiff O, Esler JG, et al. Wave patterns generated by an axisymmetric obstacle in a two-layer flow. Exp Fluids. 2013;54(12):1618.
21. Lofquist KEB, Purtell LP. Drag on a sphere moving horizontally through a stratified liquid. J Fluid Mech. 1984;148(1):271-283.
22. Bonneton P, Chomaz JM, Hopfinger EJ. Internal waves produced by the turbulent wake of a sphere moving horizontally in a stratified fluid. J Fluid Mech. 1993;254(1):23-40.
23. Radko T. Ship Waves in a Stratified Fluid. J Ship Res. 2001;45(1):1-12.
24. Moody ZE, Merriam CJ, Radko T, Joseph J. On the structure and dynamics of stratified wakes generated by submerged propagating objects. Journal of Operational Oceanography. 2017;10(2):1-14.
25. Motygin OV, Kuznetsov NG. The wave resistance of a two-dimensional body moving forward in a two-layer fluid. J Eng Math. 1997;32(1):53-72.
26. Greenslade MD. Drag on a sphere moving horizontally in a stratified fluid. J Fluid Mech. 2000;418:339-350.