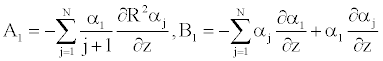Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2013) Volume 3, Issue 4
In this work, a two dimensional model of the flow is considered, with focus on effects of the nonlinearity coefficient of elasticity, variation of the radius and the Young modulus. The model described characterizes the blood flow consecutively in aneurysms, stenoses and prostheses. We obtain in the three cases that the increase in the coeffcient of nonlinearity decreases the axial fluid velocity, and weakly influence the radial velocity. The velocity of the flow remains parabolic, decrease in the aneurys-mal bag, and increase in the stenosis when the severity of blood vessels diseases varies. We found that aneurysms of small widths present high peaks of wall shear stress, and so predisposes to the formation of thrombus. Finally, we determine the maximum value of elasticity that helps to enhance the performance of prosthesis
<Keywords: Blood flow; Stented vessel; Navier-stokes equations
Since cardiovascular diseases are one of the major causes of mortality in the world, research works on the nature of these pathologies and the techniques used for the treatment have become a priority to the entire scientific community. To treat these vascular diseases, such as atherosclerosis, aneurysms and stenoses, the endovascular technique is the more comfortable technique used. It consists of a prosthesis insertion into the diseased region, using a catheter [1].
But, the implantation of the prosthesis modifies the vascular wall, dragging a modification of the flow in the vessel. This modification of the flow can alter the wall, either at the interfaces or either on the stent itself. These, therefore, lead to the fractures of the stent, the ruptures of suture or holes in the stent coat [2]. It also appear complications as displacement of the prosthesis in relation to their initial position (migration) due to the widening of the collar of an aneurysm, or to a over sizing too important of the prosthesis [3,4]. Furthermore, some studies show that the rigidity of the prosthesis lead to its migration [5]. We can note between other of the undesirable phenomena, as the endofuites that are due to the persistence of the blood flux in outside of the prosthesis, and in the aneurysmal bac, for example [4].
Much of the works done on stents are through numerical investigations [6-9]. Tortoriello and Pedrizzetti [10] examined the effects of stent implantation using an axisymmetric 2-D numerical fluid-solid model. This analysis of pulsatile flow revealed that the compliance mismatch and overexpansion caused by the stent both enhanced the flow disruption in the stented region, thus reducing to a minimum, and causing rapid variations in flow near the stent ends. But, they disregard the effects of the nonlinearity on the wall.
In this study, we can extends the analysis of the Chakravarty and Mandal model [11], by introducing, and analyzing the effects of the spatial variation of the tube radius, and wall rigidity, as well as those of localized deformation, such as aneurysms, stenoses, atherosclerosis and prostheses. We focus on the deformation of the wall and the nonlinearity coefficient of elasticity.
The rest of the paper is therefore outlined as follows. In section 2, one can briefly present the physical and mathematical model. In section 3, one makes a mathematical development. We can give a quantitative discussion following the results obtained from numerical simulation in section 4, and the last section is devoted to some concluding remarks.
Parameters of modeling
The model in consideration here is a long narrow elastic tube filled with an incompressible, viscous New- tonian fluid. Therefore, for the modeling of this flow, one can introduce the equation presenting the mass conservation of the fluid accompanied with the Naviers-Stokes set of equations, taking into consideration the nonlinear coeficient of elasticity of the wall, and the inertial effect as
Mass conservation
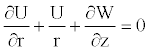 (1)
(1)
Linear momentum conservation
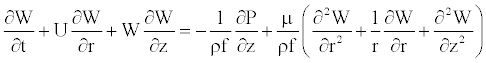 (2)
(2)
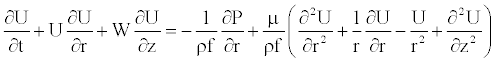 (3)
(3)
where W and U are, respectively, the axial and radial fluid velocity, P is the pressure in the vessel, ρf is the fluid density and μ is the dynamic viscosity of the fluid.
For the wall dynamics, using the second law of Newton on a portion of the vessel wall, one can obtain the relation, which can be presented as [12].
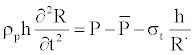 (4)
(4)
The first term in left of equality of Equation 4 is the inertia term, which is proportional to the acceleration of the vessel-wall. In the right hand side, we have the pressure in the vessel, the pressure outside the vessel, the nonlinear elastic-response of vessel, respectively. ρp is the wall density and h, the thickness of the wall assumed small compared to the radius R(z,t) of the vessel. σt is the approximation of the exponential function for the stress-strain relationship given by the authors [13,14]. This final relation used already by many authors [12,15-17] is
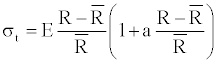 (5)
(5)
Where, R(z)=R is the stationary radius of the vessel, E(z)=E is the young modulus, and a is the coeficient representing the nonlinear coeficient of elasticity. The geometry of the vessel is described as
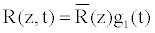 (6)
(6)
And the time dependent function g1 (t) can be approximated by [11]
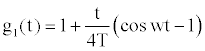 (7)
(7)
w is the frequency of heart pulsation, that is, w=2πf, f being the pulse frequency and T designates a time parameter.
As vessels segments are tapered elastic tubes with increasing rigidity away from the heart, they represent general cases of thin walled elastic tubes with variable Young modulus. Many authors [18-20] showed that the stationary radius and the Young Modulus can obey of the similar relation.
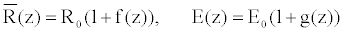 (8)
(8)
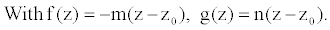
f (z) denotes the decrease of the tube radius and g(z), the increase of the tube wall rigidity along the tube originating from the heart. R0 is the radius at the entrance of the tube, E0 is the Young modulus in the undisturbed vessel and z0 the abscissa at the entrance of the vessel segment. The positive coefficients m and n characterize the rate of decrease and increase of the radius, and wall rigidity, respectively.
4.4 Modelling of arterial diseases
Here, we consider diseases as localized perturbations. These diseases are generally of three types, namely aneurysms, stenoses and atherosclerosis. At the aneurysm site, the wall is stiffer than in the normal vessel. It dilates gradually [21], tending to a more spherical shape. This implies that the mathematical model used for an aneurysm will take into consideration the gradual variation in shape and stiffness. Noubissie and Woafo [15,16] proposed a model presenting both the shape and rigidity perturbation, based on the formulae
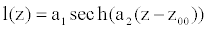 (9)
(9)
a1 and a2 are respectively the height and the gradient scale of the deformation, and z00 is the location of the center of the deformation (Figure 1). a1 is also considered as the severity of the deformation. In this study, we can use this relation, where a1>0 stands for aneurysm and a1
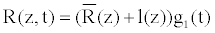 (10)
(10)
Where, t is the time, z the coordinate along the vessel axis. This model is well to study the diseases of vessels when the complicated aspects of bow and tortuous aneurysms are not envisaged.
Boundary and initial conditions
As the blood particles adhere to the inner surface of the arterial segment, the velocity of the flowing blood particles on the arterial wall surface may be taken to be equal to the velocity of the wall. This can be given mathematically as
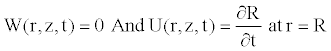 (11)
(11)
Due to the axial symmetry of the tube and the consideration of the no-slip condition, we know that the axial velocity should be maximal on the axis function of r, and the radial velocity should be zero. These conditions also used in some works [11,22], are written as
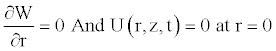 (12)
(12)
In our study associated with the femoral artery, the initial condition takes the general form [12]
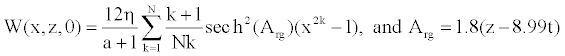 (13)
(13)
The condition for the conservation of mass of the wall, is Rh=R0 h0, where R0 and h0 are the stationary values of R and h, respectively.
Method of solution
For the reasons of simplification of the equations governing the blood flow, we can now introduce the dimensionless radial coordinate transformation, given by
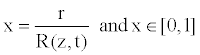 (14)
(14)
Therefore, the equations 1-3 governing the blood flow together with conditions Equations 11-13 take the form
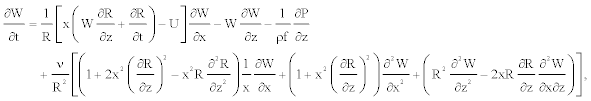 (15)
(15)
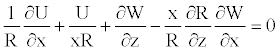 (16)
(16)
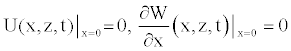 (17)
(17)
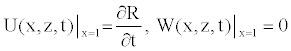 (18)
(18)
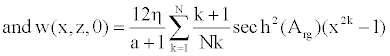 (19)
(19)
Where the radial Navier-stokes equation (Equation 3) is simply reduced to 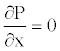 [22].
[22].
Multiplying the continuity (Equation 16) by xR, and integrating with respect to the radial coordinate between zero and x, the radial velocity becomes
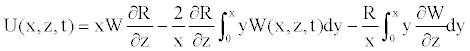 (20)
(20)
This equation can be rearranged as
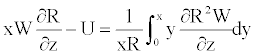 (21)
(21)
Using the boundary conditions Equation 18 in Equation 21, one obtains the following relation
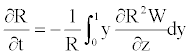 (22)
(22)
By inserting (Equations 21, 22), and Equation 4 in Equation 15, the blood motion equation appears as
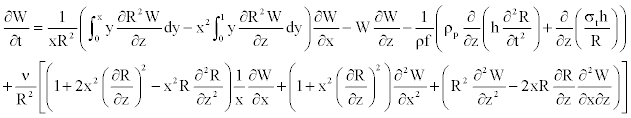 (23)
(23)
To solve Equation 23, we consider that the solution W (x, z, t) is approximated by a linear combination of a set of N functions satisfying the boundary conditions [11,22].
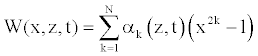 (24)
(24)
The insertion of the series (Equation 24) into the axial component of the Navier equation (Equation 23) leads to the following form
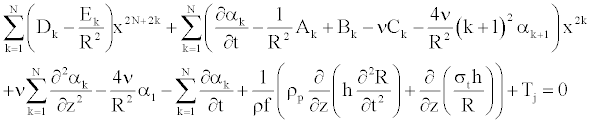 (25)
(25)
To solve Equation 25 numerically, we determine the coefficient αk [11], such as Equation 25 becomes (appendix).
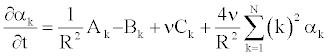 (26)
(26)
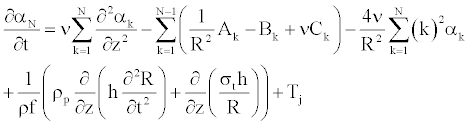 (27)
(27)
Where the expression of the radial velocity is
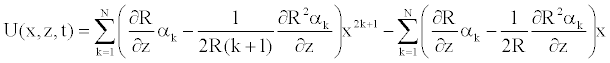 (28)
(28)
Wall shear stress (WSS) is the force exerted by flowing blood within the vessel, and is important factor in the study of blood flow. Accurate predictions of the distribution of the wall shear stress are particularly useful for the understanding of the effect of blood flow on endothelial cells. In this paper, numerical studies have been carried out on pulsating flow through various types of pathologies, and tapered vessels with the main assumptions above. The expression for the WSS can be obtained from
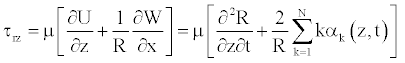 (29)
(29)
However, to determine the impediment to blood flow, another parameter called (Peripheral Resistence) is used. To quantify this effect, we compute the resistance of the flow in the vessel, posed as
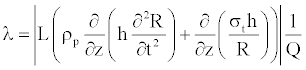 (30)
(30)
Finally, we can solve Equations (26)-(27), with Equations (17)-(19) numerically.
Numerical consideration
The problem of solving, Equations (1)-(3) with respect to r, z, and t was reduced to the solutions of Equations (26)-(27), with respect to z, and t only. The z-axis is discretized by uniformly spaced mesh points, and the partial derivatives with respect to z were approximated by a finite difference centered scheme. The Runge-Kutta algorithm is used to solve the nonlinear ordinary differential equations, the time and space steps are taken to 0.001 s and 0.2 mm, respectively. During the computational procedure, we can used the characteristic parameters for the femoral artery of a dog [12,17]: R0=1.5 mm, ρf=1050 kg/m3, ρp=1060 kg/m3, E=14.1×105 Pa, μ=0.0035 N m−2 s, z0=0, N=5, η=0.0014, f=1.2 Hz, T=1 s and L=40 mm.
Flow dynamics in the presence of aneurysms
By using the models as mentioned above, numerical results were searched in order to estimate the con- tributions of the different physical parameters to the present phenomenon. Figure 2 presents the variation of pressure when the severity varies, but the width of the diseased region of the vessel is unchanged (a2=0.1756 mm-1), for z=15 mm, and t=0.5 s. The pressure variation presents a bell shape its peak increases as the severity increases. In the same conditions, the axial velocity presents a parabolic profile, decreases when aneurysmal severity increases, and is therefore, comparable to the results so far obtained [11,17].
Various studies take into account hypotheses of the linear elastic behavior of the vessel wall [10,23]. As mentioned above, we consider in this work the quadratic nonlinear elastic aspect of the vessel wall, and we, therefore, evaluate the effect of the nonlinear elastic coeficient on the flow parameters, particularly in the aneurysm site. The increase of parameter a decreases the axial velocity profile in the aneurysm site (Figure 3), but these variations are less visible for the radial velocity. Moreover, the pressure increases with this coeficient. In the case of a healthy vessel (a1=0), we observe a constant profile of the WSS (τrz0 = 0.024 N m−2). In the presence of aneurysm but far from the disease region, the WSS maintains a constant value τrz0. At the entry of the aneurysm site, the WSS increases and attains a maximum, but decreases before the peak of the aneurysm. However, after this peak, the WSS presents symmetry over the constant value. In Figure 4, one considers aneurysms of same severity (a1=0.3), but different widths. For aneurysms of small width large values of a2, one observes important value of the WSS extrema. However, these extrema diminish as aneurysm enlarges.
Flow dynamics in the presence of stenoses
The results presented in Figure 5 illustrate the radial velocity profiles when the severity varies in stenosis, but the width of the disease region of the vessel is unchanged (a2=0.1756 mm−1), at t=0.5 s for z=15 mm. The radial velocity field retains a parabolic profile [11,24], and increases when the severity of stenosis increases, due to the obstruction of the artery lumen by the presence of the plaques of atherome. The increase of the nonlinearity parameter a, decreases the axial velocity profile in the stenotic region. The curves representing the axial flow velocity retains a parabolic shape, and are, therefore, comparable of the results obtained by Chakravarty and Mandal [11]. These effects of the nonlinear elastic coeficient (a) on the radial velocity are also negligible as in the case of aneurysm. In Figure 6, one considers stenosis of same severity (a1=−0.5), but different widths (a2) at t=0.5 s. In the case of a healthy vessel (a2=0), we observe a constant profile of the WSS (τrz0=0.024 N m−2). In the presence of stenosis but far from the disease region, the WSS maintains a constant value τrz0. Before the stenosis region, the WSS presents a value larger than (τrz0), attains a minimum, but increases in the throat of the stenosis [24]. However, after this peak, the WSS presents symmetry over the constant value. For stenosis of small width large values of a2, one observes important value of the WSS extrema. However, these extrema diminish as stenosis enlarges more and more.
It is known that the high wall shear stress may damage the vessel wall, and cause intimal thickening, which leads to platelets aggregation, and finally results in the formation of thrombus in the vessel [24-26]. Pathologies (aneurysms, stenoses) of small width occasions high wall shear stress; these, therefore implies that, aneurysms and stenoses of small width are more susceptible to the formation of thrombus.
Flow dynamics in presence of prostheses
The endovascular techniques permit to treat the pathologies, such as aneurysms or stenoses, while using the implantation of the prostheses in the aneurysmal bag or in the stenosis. These prostheses have for goal to warn the collapse of a stenosis or the rupture of an aneurysm. For the numerical simulation, we consider that the insertion of prosthesis is modeled by a possible small increase of the reference vessel radius, followed by the increase of stiffness. Furthermore, this modification affects the tube geometry in the same manner as the wall stiffness, and are specified by arbitrary, rapidly changing function.
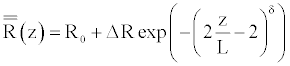 (31)
(31)
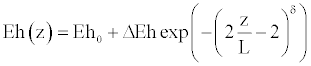 (32)
(32)
In the above equations, R(z), and Eh(z) are respectively the new expression of reference vessel geometry, and elasticity along the wall, taking into account the insertion of the prosthesis. L is the length of the inserted stent, δ gives the steepness of the transition between the normal and the stented regions (here δ=8 as in reference [10]). ΔR and ΔEh are the deformation of the vessel after the implantation of the prosthesis, and the maximum specific variation of elasticity, respectively.
In this case, the geometry of the stented vessel is now expressed as
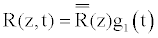 (33)
(33)
Several complications can occur after the setting up of vascular endoprostheses. In this part, we can analyze some factors capable to influence the apparition of these complications. We can present here the velocity profile, the resistive impedance and the distribution of the wall shear stress, according to the parameters as the nonlinearity, the stiffness and the transverse distortion of the wall owing to the pose of the prosthesis. In Figure 7, we can evaluate the effect of the nonlinear elastic coeficient on the flow parameters (here the axial velocity), at t=0.5 s through the prosthesis. The axial velocity profile is parabolic [14], and decreases for the positive values of a, but is insignificant for the radial velocity. We show that the changes induced by the consideration of a is observable in the velocity shape at the edges of the stent. Figure 8 illustrates the results for the variation of the resistive impedance on the parameter of rigidity ΔEh at t=0.3 s. The local increase in rigidity forms the instability characterized by lifting, and subsidence to the concave zones of the prosthesis. The fluctuations of the impedance at the site of the transition zones between the normal and stented regions could be at the origin of the secondary affection. For small values of ΔEh17, the impedance becomes large, occasioning dificulties for the blood flow. This can be at the origin of the thrombus. The high impedance to the level of the zones of sutures can lead to the fractures of the stent, the ruptures of sutures or holes in the stent coating [2,5]. Considering these results, ΔEh=17 appears as an appropriate value for a good prosthesis, as the profile of impedance is soft to the level of the swelling zone.
The wall shear stress distribution is an important diagnostic factor to examine the flow characteristics of blood through the prosthesis. In the case of a healthy vessel (ΔR=0, ΔEh=0), we observe a constant profile of the WSS (τrz0=0.00075 N m−2). In the presence of the prosthesis and for its different configuration, the WSS maintains a constant value (τrz0=0.00075 N m−2) to the entrance of the prosthesis and present large zones of instabilities characterized by the lifting, and subsidence in the bell shape profile to the level of the swelling zones. However, in the regions between the swelling zones, we have a quasi-uniform behavior of wall shear stress at t=0.7 s (Figure 9). From Figure 9, we have observed that for small distortions of the vessel in the presence of the prosthesis, one observes important value of the WSS extremums. These large instabilities in the suture zones influence the local hemodynamic, affect the life span of the prosthesis and indicate a more thrombogenic risk into the upstream edge [27,28].
A two dimensional model of the flow is considered in this work, with focus on effects of the nonlinearity coeficient of elasticity, variation of the radius and that of the Young modulus. These are characteristics of blood vessels in presence of aneurysms, stenoses and prostheses. Two problems are thus considered in the paper. First of all, we have studied the different behaviors of a blood flow in presence of aneurysm and stenosis. By varying the vessel parameters related to the diseases, and the coefficient of nonlinearity of the wall, we have analyzed their influences on the dynamics of the blood flow. The second problem analyzed is that of the effects of prosthesis. We have study here the modifications that occur at the time of the use of invasive technical treatment of vessel pathologies via endoprostheses. The numerical results presented here allowed us to interpret some ominous phenomena observed at the time of the poses of the endoprostheses. However, the high impedance to the level of suture zones can lead to ruptures of sutures, fracture to the stent or holes in the stent coating.
The insertion of the series Equation 24 into the axial Navier equation 23, leads to the following form
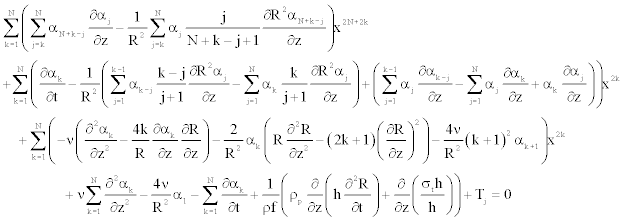
Either again we have
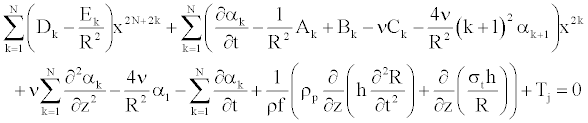
Where
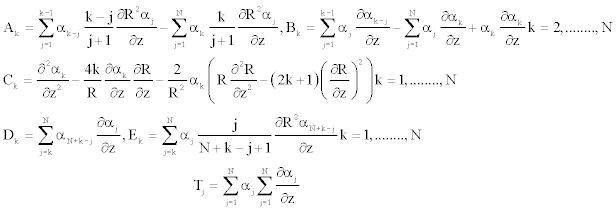
And