Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2017) Volume 6, Issue 3
This study focuses on the development, validation and application of the interdisciplinary computational fluid dynamics/computational aeroacoustics (CFD/CAA) method with the name Flight-Physics Simulator AEOLus (FPSAEOLus). FPS-AEOLus is based on enhanced conservative, anisotropic, hybrid Reynolds-averaged Navier-Stokes/ Large-Eddy Simulation (RANS/LES) techniques to solve an aerodynamic flow field by applying the unsteady, compressible, hyperbolic Navier–Stokes equations of second order.
The two-layer SSG/LRR- ω differential Reynolds stress turbulence model presented, combining the Launder- Reece-Rodi (LRR) model near walls with the Speziale-Sarkar-Gatski (SSG) model further apart by applying Menter's blending function F1. Herein, Menter's baseline ω-equation is exploited for supplying the length scale.
Another emphasis is put on the anisotropic description of dissipation at close distance to the solid wall or in wake area for describing the friction-induced surface-roughness behaviour in viscous fluid physics and swirling wake effects. For that purpose, the SSG/LRR-ω seven-equations Reynolds stress turbulence model with anisotropic extension was realized, therefor the theory is described in general.
Beyond that, a modified delayed detached-eddy simulation (MDDES) and a scale adaptive simulation (SAS) correction to capture the stochastic character of a large-eddy-type unsteady flow with massive flow separations in the broad band is implemented.
To demonstrate the time-dependent noise propagation having wave interference a linearized Euler equation (LEE) model using a combined Momentum- and Lamb-vector source have been applied into the CFD/CAA - method. The DLR 15 wing, a High-Lift device in landing configuration having a deployed slat and landing flap is studied experimentally and numerically. The first part of the application deals with the steady flow investigation; however, the same turbulence model is used for the unsteady flow case without the enclosed time derivatives. The second part concentrates on unsteady modelling for the Navier–Stokes and Linearized Euler field. With this new combined CFD/CAA - method, steady and unsteady numerical studies for the high-lift wing configuration for discovering the aerodynamic and –acoustic propagation effects are shown, discussed and when experimental data were available validated. The High-Lift wing has a constant sweep angle of Λ=30° to investigate possible cross-flow; to realize this, periodic boundary conditions were set in spanwise direction.
<Keywords: High-lift device, Aerodynamics, Aeroacoustics, CFD/ CAA, Navier-stokes, Conservative euler fluxes, SSG/LLR-ω Reynolds stress turbulence model, Anisotropic dissipation in tensor form, Modified delayed detached-eddy simulation, Scale adaptive simulation, Steady and unsteady iterative gauss-seidel, Linearized euler equation
Extended multi-element high-lift devices are required during the take-off and landing phases to generate the necessary lift at the aircrafts’ wing. When flying the manoeuvre they produce highly complex swirling and separating flow effects. These phenomena are composed of the boundary layer transition, turbulent free shear layers, confluent wake/boundary layer flows at the trailing edges of the slat and landing flap, and a succession of interdependent interactions of all these effects. At moderate (small) angles of attack, a separated flow is produced in conjunction with an adverse pressure gradient in the boundary layer on the suction side of the landing flap. The properties of a high-lift flow field are highly interdependent, and therefore, the numeric modelling of the fluid physics remains a major challenge. A failure in the modelling of one of these phenomena results in a malfunction in the prediction of the entire flow field of the investigated high-lift system.
In addition to the aerodynamic lift performance, the strong generation of slat and flap noise in the bays and wakes of high-lift systems have been identified as one of the most important sources of airframe noise, which has a significant effect on the aircraft design. It is known from previous investigations that the conventional Reynoldsaveraged Navier–Stokes methods (RANS) are not suitable for simulating the noise-generating sources of high-lift devices applied in aeroacoustic analyses [1] therefore, large-eddy simulation (LES) or special conservative, unsteady, hybrid, anisotropic RANS/LES simulation (HARLS) techniques have been developed for this purpose. The aerodynamic high-lift flow is related to the unsteady stochastic fluidic movements of vortex structures at various turbulent scales, which are also related to large pressure fluctuations stemming from interfering wave effects. Therefore, turbulence-resolving modelling must be used to obtain a reliable aerodynamic and aero-acoustic noise prediction for a high-lift system.
An unresolved goal is simultaneously to reduce the noise footprint, and therefore, to apply the new functionalities of high-lift and cruise systems with modern structural concepts as well as active turbulent flow control to minimize the take-off and landing approach distances during flight.
The development of an improved, accurate and validated hybrid computational fluid dynamics/computational aeroacoustics (CFD/ CAA) method to compute the aerodynamic and aeroacoustic field concurrently brings a huge benefit for the future aircraft layout. To predict noise propagation and apply it in an acceptable industrial design cycle can greatly benefit the assessment and optimization of upcoming aircraft configurations by improving their aerodynamic efficiency using modern noise- and fuel-reduction concepts.
This study deals with the determination of aerodynamic efficiency and reduction of noise sources, thus resulting in flight with extended high-lift flaps during the landing approach. During the landing approach, the flaps are reeled-out to produce the necessary lift. An aircraft in the landing configuration essentially consists of one or more trailing edge flaps and one or more leading edge flaps. The aforementioned flaps, spoilers, and ailerons produce a dominant aeroacoustic noise. Therefore, the reduction of the noise is, in principal, an interdisciplinary process. In such a case, the improvement is always a compromise in the performance of the aerodynamics and weight. Here, the safety of the overall flight behaviour is considered to be the most important in the design process and must be fulfilled.
The focused conservative, hybrid, anisotropic RANS/LES modelling aims at turbulence-resolving simulations, in particular, for unsteady flows with massive flow separation in a broad bandwidth and extensive vortex motions, which benefit from the computational efficiency of RANS and the computational accuracy of LES and scale adaptive simulation (SAS). For the physical mechanism outlined above, a highly accurate aerodynamic model is required to obtain an acceptable prediction.
Therefore, a conservative, convective formulation has been developed and implemented in the Flight-Physics Simulator AEOLus (FPS-AEOLus). The current widely used approach is based on the conservative characteristic based method/flux-vector splitting (CBM/ FVS) scheme mentioned in Eberle [2-5] while the viscous part of the solver concentrates on investigations using the anisotropic Reynolds stress turbulence method as presented by Schneider [6]. In order to simulate unsteady large viscous eddies, detached-eddy simulations (DESs) are conducted. In the present study, a further-improved modified delayed detached-eddy simulation (MDDES) term, as mentioned by Zhao [7], as well as a scale adaptive simulation (SAS) term, from Menter and Egorov [8], was included in the method to develop a nonzonal method with embedded LES capabilities. Within the mentioned MDDES, a wall-functioned LES approach with improved shielding in the RANS region and sensors that can detect and identify vortexes are used. Both the MDDES and SAS extensions use physical descriptions to model the complex flow separation in contrast to older DESs in which grid sensitivities have been used. Spalart [9] first proposed the DES as a hybrid RANS/LES technique for the prediction of turbulent flows at high Reynolds numbers Spalart and Deck [10]. The development of the RANS/LES technique was inspired by CPU time estimates that indicate that the computational costs of using an LES only to complete configurations such as an airplane or its components, e.g. the wing tip and wing/pylon/turbine are immensely high. In particular, when applied to high Reynolds number conditions, the grid resolution required in the boundary layer is very fine, which is an issue that exists even when fully successful wall-layer modelling is used. Usually, high-Reynolds-number separated flows can be predicted using the solutions of the steady RANS or unsteady RANS ((u)RANS). One disadvantage of RANS methods applied to massive separations is that the statistical models are designed and calibrated based on the mean parameters of thin turbulent shear flows containing numerous relatively ‘normal’ eddies. Such eddies are not representative of the comparatively fewer and geometry-specific structures that typically characterize massively separated flows. The advantages then offered by LES provide strong motivation for its application, such as the direct resolution of the dominant unsteady turbulent structures. In addition, while RANS or (u)RANS does not appear to constitute a viable long-term approach for predicting massively separated flows at high Reynolds numbers, the calibration range of most models is sufficient to yield an acceptable accuracy of a relatively broad range of attached flows.
In the MDDES, the aim is to combine the most favourable aspects of the two techniques, i.e., the application of the RANS models for predicting the attached boundary layers and LES for the resolution of time-dependent three-dimensional large eddies within the non-zonal definition. The cost scaling of the method is then favourable as LES is not applied for the resolution of the relatively smaller-structures that populate the boundary layer. The MDDES belongs to the non-zonal category of the DES set of improvements; it is a further development of the improved delayed detached-eddy simulation (IDDES), which uses more elaborate sensor to switch from the RANS to LES region. The IDDES takes into account the mismatch of the boundary layer in the typical DES concept.
In regular applications of the method, the entire boundary layer is treated by RANS and with an LES treatment of the separated regions. One of the issues with hybrid RANS/LES methods is the ‘grey area’ in which, after separation, a shear layer must generate LES-content (random eddies) that it did not possess in the boundary layer upstream. The process of generating LES content is more easily accommodated by a thin shear layer that is rapidly departing from the wall and in configurations with fixed separations (e.g. as occurs for geometries with sharp corners).
The time-dependent effects of the viscosity are supported by an additional one-equation non-linear eddy-viscosity transport model (NLEVM) presented by Revell [11]. More realistic pressure fluctuations are obtained using different wall-roughness models that are presented by Wilcox [12] and Menter [13].
At Airbus Group Innovations, an unstructured, unsteady, conservative, upwind-oriented, HARLS method called FPS-AEOLus was developed by Schneider [6] to solve the Navier–Stokes equations.
To simulate the detailed physics for obtaining the flow calculation, the following have been used as enhancements to the flow method:
• Conservative convective flux, combined Riemann/Eigenvector flux CBM/FVS,
• NLEVM,
• Seven-equations SSG/LRR-ω Reynolds stress model,
• Dissipation term ω based on Menter’s length-scale equation:
i. Fully tensor form near the body to gain anisotropic relations and
ii. Excited by MDDES to switch from RANS to LES.
• Cross-diffusion term of the turbulence model brought into excitation by adding SAS correction,
• Iterative, implicit Gauss–Seidel (GS) scheme for time integration update.
This study shows the results of a turbulence-resolved simulation for a three-element high-lift aerofoil in the landing configuration. All slats, flaps, and wing elements of the high-lift configuration presented were constructed with blunt trailing edges. The simulation flow velocity was set to v=55 m/s, which is typical for a landing approach, and the timestep size is defined as Δt=0.00001 s for the unsteady simulation. A quasi– two-dimensional simulation is used with an angle of attack of αeff=4.28°, which means it has only one grid layer in the spanwise direction, but it allows the demonstration of cross flow. The wing section has a constant sweep angle of Λ=30° in order to represent the infinite free-flight model. The sweep angle effects are numerically solved with a periodic boundary condition to enable a nearly spanwise cross flow.
The wind tunnel measurements have been performed in the “Deutsch Niederländische Windkanäle” (DNW) large low-speed facility (LLF) in Marknesse, Netherlands [14]. The aeroacoustic wind tunnel typically has a closed air-circulation measurement chamber, but it can also be considered to be open. The nozzle diameter is 8 m × 6 m with possible wind velocities of 0 ≤ u ≤ 80 m / s . The wing is anchored in a bracket and can be adjusted using the remote control (left).
Aerodynamic measurements of the surface pressure and farfield acoustic measurements were performed. Sound localization using a cruciform arrangement of microphone arrays was used to supplement the measurement program, Reichenberger [15].
DNW is one of Europe’s most advanced and specialized organizations for wind tunnel testing. DNW’s 11 wind tunnels include subsonic, transonic, and supersonic facilities and provide experimental aerodynamic simulation capabilities for low velocities. This includes all aspects of airflow encountered in nature and for engineering requirements.
DNW provides techniques for aerodynamic, aeroacoustic, or aeroelastic simulations and tests of scale models in a controlled environment. Its experimental simulation techniques capture the essence of the issues to be investigated.
The FPS-AEOLus uses a CFD method to model the aerodynamic flow field by applying the compressible, unsteady, hyperbolic Navier– Stokes differential equations of the second order. The present method explores the time-accurate unsteady behaviour of compressible aerodynamic fields with large moving vortex structures over a broad range of the turbulent scale.
The attitude of the current FPS-AEOLus package is to build a strictly conservative, unsteady, upwind-oriented HARLS formulation to determine the aerodynamics and sound propagation to emphasize anisotropic dissipation, e.g. roughness-induced friction at various flight conditions as studied by Eberle [2,5] and Schneider [6].
The RANS equations describe the time-accurate behaviour of compressible flow fields. The RANS and LES are used to calculate the averaged mean states of the flow field and unsteady large-eddy structures, respectively.
The aerodynamic field equations are solved using an unstructured, hybrid computational primary grid consisting of primitive elements such as tetrahedron, hexahedra, pyramids, and prisms. The primitive grid is rearranged to yield a dual grid, where the finite-volume method is applied (Figure 1). In volume-based cell-centred grid elements, the hulling area is split into ‘inner’ and ‘outer’ faces. The outer surface bears the necessary flow boundary conditions for the simulation, e.g. farfield, inviscid Euler wall, viscous wall, pneumatic actuator, and symmetry. On the inner faces, the Riemann-problem is applied for the flux formulation (Figure 2).
The full description of the inviscid flow has been provided by Eberle [2-5], Chakravarthy [16], Liou [17,18], Roe [19], Schmatz and Brenneis [20], Steger and Warming [21], and Van Leer [22]; this includes a strictly conservative CBM/FVS technique with the capacity to prevent large unphysical flow dissipation and is characterized by strong robustness and accuracy. The CBM/FVS flux describes the homogeneous solution of the compressible, hyperbolic Navier–Stokes equations and is a combined, blended Riemann–Eigenvector flux for representing inviscid flow phenomena in a sophisticated balanced combination Drikakis [23, 24].
The seven-equations SSG/LRR-ω turbulence model Bosco [25,26] is chosen to model the turbulent Reynolds stresses to capture anisotropic viscous vortex mechanisms Eisfeld [27-29], Launder [30], Speciale [31], Bentaleb [32], Ferziger [33], and Jeyapaul [34]. For the dissipation transport, the Menter [13] length scale form is selected, while in the Hanjalić, Jakirlić, and Hadžić (HJH) model, a homogenous dissipation is considered [35]. Herein, the entire Reynold’s stresses and the dissipation are modelled in tensor form in the near-wall region. By applying various extension terms, the turbulence model was generalized such that the rotation and curvature effects as well as pressure and compressibility mechanisms are physically described. To handle anisotropic dissipations that occur in the near-wall region of the body’s geometry and wake areas, a blended anisotropic dissipation model obtained by combining the HJH model [35] with the Lai and So model [36] is considered. The local distribution of the isotropic and anisotropic dissipation is determined using an anisotropic transition function in a Newton iterative approach. The dissipation in the free-stream field is assumed to be quasi-isotropic Schneider [6].
It should be pointed out that, in addition, a two-equation kω-SST turbulence model from Menter [13] and Hellsten [37-39] is coupled with an available explicit algebraic Reynolds stress model presented by Johansson [40] and Wallin [41] to improve the anisotropic viscous character of the flow field Schneider [6] (Figure 3).
The NLEVM describes the unsteady behaviour of large-scale vortex topologies [11]. In the steady case, all time derivatives in the NLEVM are set to zero. The production and movement of large-eddy turbulent structures is characterized with the SAS, which was presented by Menter and Egorov [8], to oscillate or excite the cross diffusion term in the turbulence model, but in this formulation, it was applied to obtain a full Reynolds stress model. The unsteady viscous behaviour of LES flow is modelled using the NLEVM. The SAS and NLEVM correction terms both belong to the (u)RANS modelling class, while the production and movements of large-scale vortexes are handled by the DES-type models Peng [42-45] and Grundestam [46]. These DES models are used in addition to exciting the dissipation term of the turbulence model Spalart [47, 48], Nikitin [49], Travin [50], Menter [51], Gritkevitch [52] and Sainte-Rose [53].
The LES modelling is classified into two different types: non-zonal modelling approaches and zonal modelling approaches. In the present code, an advanced MDDES (Zhao [7]) has been implemented, which belongs to the class of the non-zonal rough-structure models and is used to excite the dissipation of the turbulence model.
Here, the non-zonal modelling refers to seamless hybrid methods where the RANS-LES interfacing location is defined inherently in the modelling formulation, such as the DES-type methods [54, 55]. The zonal modelling here refers to hybrid models in which the RANS/ LES interfacing location is prescribed based on the requirement of the computation, in that context please find the embedded LES approach derived by Deck [56-62].
The advantage of the aforementioned SAS and MDDES correction is that no computational grid dependency is provided, while physical values or sensors are used to switch from RANS to LES and vice versa. In Temmerman [63], Van Driest [64], Vatsa [65], and You [66], advanced RANS/LES methods are applied, compared, and validated.
To represent better the flow friction produced owing to surface roughness, certain sand-grain roughness models derived by Wilcox [12] and Menter [13] are used to complete the general turbulence model. Within the HARLS process described here, the NLEV are applied in both the steady and unsteady update scheme; however, in the steady mode, the terms having time-derivatives are not taken into account [11].
The unsteady time integration of the aerodynamic fields is performed with an iterative, implicit GS method [6], which is from second order in time.
In the next chapter, the SSG/LRR-ω Reynolds stress turbulence model and the anisotropic dissipation is written more precisely. To yield the highest-level approximation of the Reynolds stress tensor that can be achieved by employing differential Reynolds stress models. In these cases, the eddy-viscosity hypothesis is removed completely from the six transport equations for the components of the Reynolds stress tensor and an additional equation has to be solved for the turbulent length scale ω that is required for the closure.
SSG/LRR-ω Reynolds Stress Turbulence Model
The 7-equations SSG/LRR-ω Reynolds stress turbulence model by neglecting the effects of buoyancy and system rotation can be written in terms as follows:
1.  Production term of the Reynolds stress,
Production term of the Reynolds stress,
2.  Pressure-strain correlation tensor, or also, redistribution term,
Pressure-strain correlation tensor, or also, redistribution term,
3. Destruction term of dissipation tensor,
Destruction term of dissipation tensor,
4. Diffusion tensor,
Diffusion tensor,
5. Fluctuation mass-flow caused of the compressibility in the fluid and
Fluctuation mass-flow caused of the compressibility in the fluid and
6. Right-hand side excitation vector to model the Reynolds stress τij.
Right-hand side excitation vector to model the Reynolds stress τij.
7. For this, the components  of the Reynolds stress, which correspond with the negative shear stresses, -τij. will be charged immediately:
of the Reynolds stress, which correspond with the negative shear stresses, -τij. will be charged immediately:
 (1)
(1)
The term  defines the symmetric tensor of Reynolds stress differential turbulence model.
defines the symmetric tensor of Reynolds stress differential turbulence model.
Herein the upper line - highlights a simple value averaging. The roof ^ suggests a Favre - (or mass) averaging. The simple ´ or double ´´ instructs to the corresponding fluctuations, respectively.
The Reynolds stress model is having a second-order closure condition. In this context, this means that the correlations of second order for the velocity components are calculated, but the higher order correlations have to be modelled. To formulate equations, which describe the Reynolds stresses, the momentum equation of the Navier- Stokes equations must be used. When multiplying the momentum equation with the components of the fluctuation velocity as well as a time dependent averaging of this product. If the operator N represents the Navier-Stokes equation, we get:
 (2)
(2)
Starting from the exact form of the momentum equation, the Reynolds stresses can be derived as follows:
 (3)
(3)
The length-scale equation for the specific dissipation rate ω can be read:
 (4)
(4)
The elements of the Reynolds stress production tensor,  , are functions of the Reynolds stresses
, are functions of the Reynolds stresses  and the derivatives of the mean velocity components
and the derivatives of the mean velocity components  as
as
 (5)
(5)
The term of redistribution, known also as the pressure-strain correlation, is:
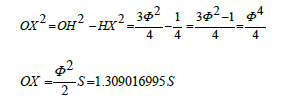 (6)
(6)
The pressure-strain correlation tensor is modelled by neglecting the effects of pressure dilation as:
 (7)
(7)
The coefficients have been calculated by inserting the values from the Tables 1-4 and using the blending function (equation 17), which will be described below.
| Variable | C1 | C1* | C2 | C3 | C3* | C4 | C5 | D(GGD) |
|---|---|---|---|---|---|---|---|---|
| LRR | 1.8 | 0.0 | 0.0 | 0.8 | 0.0 |  |
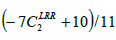 |
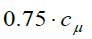 |
| SSG | 1.7 | 0.9 | 1.05 | 0.8 | 0.65 | 0.625 | 0.20 | 0.22 |
Table 1: Description of seven attributes of reading comprehension difficulty of STEP-RC items.
| Variable | αω | βω | σω | σd |
|---|---|---|---|---|
| LRR | 0.556 | 0.075 | 0.5 | 0 |
| SSG | 0.44 | 0.0828 | 0.856 | 2σω |
Table 2: Closure-coefficients of the length-scale equation ω.
| Velocity | 55 m/s |
| Mach number | 0.16 |
| Temperature | 293 K |
| Steady pressure | 101325 Pa |
Table 3: Aerodynamic state variables.
| Thickness of first cell heights | 1.0e-06 |
| Number of layers | 30 |
| Stretching factor | 1.15 |
Table 4: Input parameters of the hybrid grid generator CENTAUR.
Herein now is 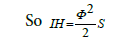 the second invariant of the Reynolds stress anisotropy tensor
the second invariant of the Reynolds stress anisotropy tensor  , as follows:
, as follows:
 (8)
(8)
and the mean rate of rotation tensor can be defined as:
 (9)
(9)
The Destructions term  or also named as dissipation, we have:
or also named as dissipation, we have:
 (10)
(10)
For an isotropic modelling of dissipation 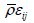 , we use:
, we use:
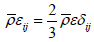 (11)
(11)
and represents the turbulent fluctuations in conjunction with the molecular viscosity.
Herein is  the scalar dissipation and
the scalar dissipation and 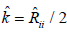 the value for the turbulent kinetic energy. We set the constant Cμ=0.09. The model constants used in the present work have been shown in Table 1, which are divided into inner ω and outer ε coefficients. The variable μt is the turbulent viscosity (called the turbulent Eddy viscosity) and holds no physical relation with the dynamic viscosity.
the value for the turbulent kinetic energy. We set the constant Cμ=0.09. The model constants used in the present work have been shown in Table 1, which are divided into inner ω and outer ε coefficients. The variable μt is the turbulent viscosity (called the turbulent Eddy viscosity) and holds no physical relation with the dynamic viscosity.
To the diffusion-term 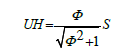 applies:
applies:
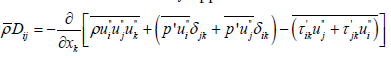 (12)
(12)
The diffusion-term is formed from the turbulent transport, the pressure diffusion and the viscous diffusion terms, together.
Based on a general gradient-diffusion hypothesis, we get the diffusion term:
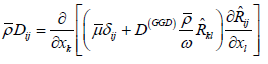 (13)
(13)
Where 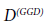 describes the diffusion coefficient and is calculated according to the following equation:
describes the diffusion coefficient and is calculated according to the following equation:
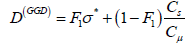 (14)
(14)
The abbreviation GGD means generalized gradient diffusion.
Herein is F1 the original blending function due to Menter [13] (equation 17), with the constants σ*=0.5 and Cs=0.22. The function F1 was developed in a way to be equal to 1 starting from the wall up to approximately 50 percent of the boundary layer and after that it tends gradually to 0. The blending function depends on global fluid properties, such as dynamic viscosity and fluid density, and on turbulence-related quantities, such as turbulent kinetic energy and specific dissipation rate, and it also takes into account the distance d of the cell to the nearest viscous wall as
 is the deformation velocity, or even called shear-rate tensor.
is the deformation velocity, or even called shear-rate tensor.
 is the „trace-less“ shear-rate tensor.
is the „trace-less“ shear-rate tensor.
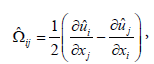 as the anti-metric rotation velocity, or swirl tensor.
as the anti-metric rotation velocity, or swirl tensor.
The definition of the shear-rate tensor  is symmetric.
is symmetric.
Now the contributions of the fluctuating mass flow  are:
are:
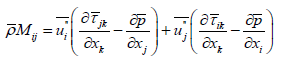 (15)
(15)
All previously listed terms have to be modelled. The SSG/LRR-ω blending function corresponds to the 2-equation k-ω SST model by Menter [13] and Eisfeld [27,28].
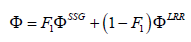 (16)
(16)
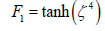 (17)
(17)
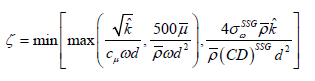 (18)
(18)
With d as the smallest wall distance.
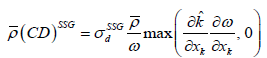 (19)
(19)
As the cross-diffusion term 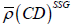 from equation (4), the coefficients of the ω length-scale equation are taken from Table 2.
from equation (4), the coefficients of the ω length-scale equation are taken from Table 2.
As we recognize, during modelling of the Reynolds stress equation an isotropic dissipation rate ε is taking into account. This creates a close dependency to the length-scale equation ω. Because the SSG model was developed based on the ε -equation, some close wall modifications are required that enable a coupling ω-equation model with the BSL, to approach the wall effects with the ω-equation.
Wilcox [12] was able to show that the Launder-Reece-Rodi (LRR) model can simply combined with the ω-equation, when ignoring the effects of wall reflections. The corresponding pressure-strain correlation can be transformed into the same form as equation (7), so that the same blending technique as in the Menter’s BSL ω-equation model can be applied. The analogue procedure applies also to the diffusion coefficient D(GGD). Due to this close wall modifications, the model is called now SSG/LRR-ω, Eisfeld [28].
The closure coefficients, which describe the SSG model (Speziale, Sarkar and Gatski) and the LRR model are summarized in Table 1. It should be noted that the values for the diffusion coefficient 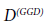 and
and 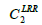 easily compared to reference Cecora and Eisfeld [29]. They have been changed to match better the logarithmic layer in a boundary layer without pressure gradient.
easily compared to reference Cecora and Eisfeld [29]. They have been changed to match better the logarithmic layer in a boundary layer without pressure gradient.
The closure-coefficients of the length-scale equation ω are listed in the Table 2.
The production and the dissipation term are often the biggest contributor of this balance and therefore play a major role. They both are responsible to generate the turbulence of velocity gradients and their decay. Apparently, turbulence is generated only in a flow with time averaged velocity gradients and in shear dominant flow. The velocity gradient is the motor of the turbulence. The required energy is eliminated from the main fluid movement. On the other hand, the dissipation reduces the turbulent fluctuations. It represents a central parameter in the theory of turbulence.
In the viscous sub-layer, the flow due to surface friction behave anisotropic, small-scale vortex structures on the solid wall, which are always in isotropic and larger in shape and size within the "free stream" regions (Figure 1).
The scalar dissipation  is formed from “half trace” of the dissipation tenor εij . The size of this variable can be found directly from the scalar length-scale equation ω in the isotropic dissipation model (Figure 4). For a Reynolds stress model the entire dissipation tenor εij must be modeled Bentaleb [32]. Since the dissipation of turbulence is related to the small-scale vortexes, which in turn are accepted in the simplest case as isotropic, applies:
is formed from “half trace” of the dissipation tenor εij . The size of this variable can be found directly from the scalar length-scale equation ω in the isotropic dissipation model (Figure 4). For a Reynolds stress model the entire dissipation tenor εij must be modeled Bentaleb [32]. Since the dissipation of turbulence is related to the small-scale vortexes, which in turn are accepted in the simplest case as isotropic, applies:
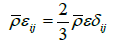 (20)
(20)
The assumption in the SSG/LRR-ω Reynolds stress turbulence model expressing, that the deviation components of dissipation tenor tend to zero. The diagonal components uniform share a scalar value one.
Taking into consideration that the dissipation tenor εij nearby the solid wall adopts an anisotropic form and in “free-flow” region, the shape is isotropic, the following tensor representation is recommended:
For the general, anisotropic dissipation model εij applies:
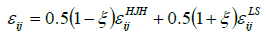 (21)
(21)
ξ is the weight parameter, which lies in the interval ξ= [-1,1], so that both anisotropic dissipation models 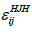 and
and 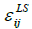 may be mixed.
may be mixed.
The anisotropic model 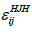 according to Hanjalić, Jakirlić and Hadžić [35]:
according to Hanjalić, Jakirlić and Hadžić [35]:
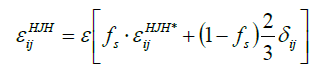 (22)
(22)
Now the inhomogeneous, tensor dissipation 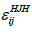 is
is
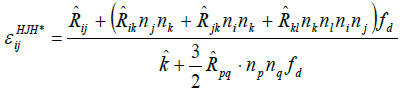 (23)
(23)
For the anisotropic mixing-function fb follows:
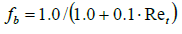 (24)
(24)
With the turbulent Reynolds number Ret:
 (25)
(25)
or the ω representation is read
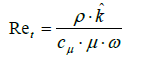 (26)
(26)
The two anisotropic dissipation tensor models use different mixing strategies, which are sensitized by means of the wall normal vector due to Jeyapaul [34] and toggle to isotropic “free field” behavior as well as in anisotropic dissipation behavior in nearby solid wall zones.
The anisotropic model 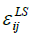 according to Lai and So [36] or:
according to Lai and So [36] or:
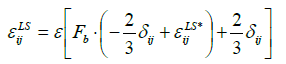 (27)
(27)
The inhomogeneous, dissipation 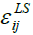 in tensor form, we have:
in tensor form, we have:
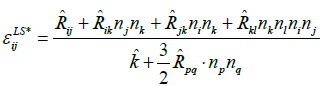 (28)
(28)
With the mixing function Fb after Lai and So:
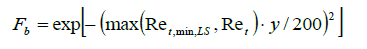 (29)
(29)
That only a thin anisotropic layer around the object is formed, in equation (4-29) a minimum turbulent Reynolds number Ret, min, LS=4.0 e+5was introduced. In addition, the wall distance y was introduced to calculate the mixing function Fb to allow a smooth decay in the flow field. Herein 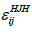 is wall unit vector in the anisotropic models (by HJH and LS).
is wall unit vector in the anisotropic models (by HJH and LS).
In some turbulence models found in literature, the anisotropic/ isotropic switching function fs is set in zones with small Reynolds number to fs =1, in the remaining computational space it is set fs =0.
The following computation of the invariants for Reynolds stresses and the tensorial dissipation εij the transition function fs is used for modelling. The transition function fs produces a “correct” transition of the anisotropic term at solid wall and the isotropic Rotta's term in “free stream” zones.
In the present formulation for the dissipation 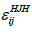 due to Hanjalić, Jakirlić and Hadžić is fs the mixing function and can be calculated as follows:
due to Hanjalić, Jakirlić and Hadžić is fs the mixing function and can be calculated as follows:
α) From the components of anisotropic turbulence:
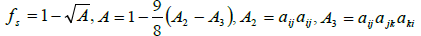 (30)
(30)
β) or the components of anisotropic turbulence as well as the tensor dissipation:
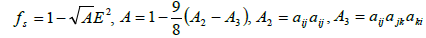 (31)
(31)
and
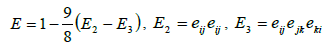
This modeling is calculated with an iteratively Newton's method, as long as, until a convergent value for the anisotropic transfer function, or a previously defined termination criterion is fulfilled. Also in this context when fs=0 is used, means isotropic turbulence.
The calculation of unsteady sound propagation occurs in a hybrid CFD/CAA method that couples the Navier-Stokes equations (NS) with the linearized Euler equations (LEE) at each time step. First, the aerodynamic fields in the time step are calculated. The unsteady Navier-Stokes field is at a physical time t transformed by means of acoustic source models and used now as an excitation term for the acoustic LEE-method at its right hand side. The solution of the acoustic propagation takes place on the same computing grid, which is used for solution of the aerodynamic field.
To prevent acoustic reflections in the flow region occasionally generated in the farfield, at the farfield a "sponge-layer" for the acoustic variables is introduced.
In the adjacent equation (Figure 5) the NS-LEE coupling during the unsteady CFD/CAA simulation is shown, where the sound propagation and the aerodynamic field are simultaneously calculated.
Applying an acoustic simulation the total flow vector 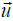 :
:
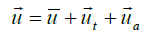 (32)
(32)
is split into an average 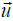 , turbulent
, turbulent 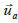 and acoustic part
and acoustic part 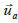 .
.
The unsteady one-dimensional differential equation of the form:
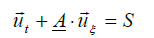 (33)
(33)
This demonstrates the relationship between the Jacobi matrix 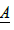 and the external source S.
and the external source S.
At defined probe locations fast Fourier transform (FFT) is applied to analyse the frequency behaviour and sound pressure level.
The simple formulation of the linearized Euler equations assumes an ideal gas without having a viscosity, so that no heat transfer or radiation, and no internal or external forces take into account and are neglected. The LE-equations are read:
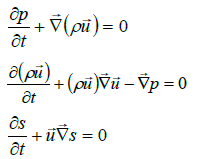 (34)
(34)
The linearized Euler equations are modelling the propagation of acoustic waves in a non-homogeneous moving medium. Both, convection and diffraction effects are taken into account. The LEequations linearize about a runtime-averaged flow condition, for that the densityρ, the pressure p, the velocity 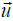 and the entropy s are split into two components. In a runtime-averaged constant flow part and in a turbulent flow component that represents the fluctuating variations about the mean flow.
and the entropy s are split into two components. In a runtime-averaged constant flow part and in a turbulent flow component that represents the fluctuating variations about the mean flow.
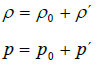
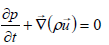 (35)
(35)
and for the entropy s´
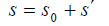
According to the development and simplification (neglecting terms of 2nd order and products of two turbulent components as well), we get:
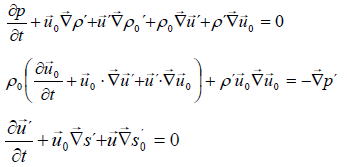 (36)
(36)
Causing of the acoustic noise can be regarded as a variation of turbulent pressure fluctuation 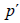 . In equation (36),
. In equation (36), 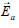 notes the entropy.
notes the entropy.
The LE-equations in incremental, primitive matrix form written, we have for the acoustical flux  the expression, now follows:
the expression, now follows:
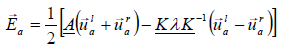 (37)
(37)
With the Jacobi matrix 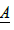 :
:
 (38)
(38)
For the eigenvalue 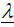 , we have:
, we have:
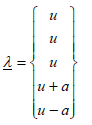 (39)
(39)
The transformation matrix 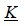 is:
is:
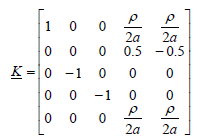 (40)
(40)
The inverse of the transformation matrix 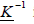 is determined like:
is determined like:
 (41)
(41)
In order to represent the sound generated by the flow turbulence in the LE-equations, suitable acoustic source terms have to be formulated and implemented. For this purpose, a new source-vector must be generated on the right hand side of the LE-equations, which is built by the velocity fluctuation of the aerodynamic Navier-Stokes field.
Momentum source 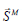 :
:
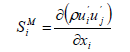 (42)
(42)
Lamb-vector source 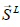 :
:
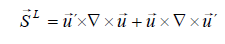 (43)
(43)
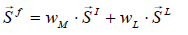 (44)
(44)
Equation (5-13) represents the variables wM and wL the weighting of the momentum and Lamb-vector source.
The acoustic source 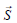 is determined as a difference from the actual sources
is determined as a difference from the actual sources 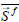 , at physical time t, minus the runtime-averaged source
, at physical time t, minus the runtime-averaged source 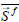 :
:
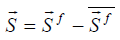 (45)
(45)
In the context of this study, a number of research projects have been conducted to investigate the aerodynamic characteristics of high-lift configurations. Previous projects were based on small-scale aeroacoustic examinations for high-lift systems. But reached their limits with regard to the aerodynamic and aeroacoustic relevance. The results of the aerodynamic measurements on very small-scale models in the wind tunnel could not be transformed into a highly complex optimization process to define the geometrical shape of civil or cargo aircraft, and therefore, we had to allow the use of 1:1-scale airplane-like configurations. In the presented project, large-scale aeroacoustic tests have been performed to produce the necessary aeroacoustic database in order to increase and specify the knowledge and understanding in the noise generation process at high-lift configurations.
As for the geometry, the DLR F15-wing with a sweep angle of Λ=30° was chosen, because an extensive measurements database is available. The selected angle for the present numerical investigations is set to α=4.28° to match the windtunnel test conditions.
The results generated in the simulations show that we also have to take into account cross-flow mechanisms to represent the sweep-angledominated flow types. This means that the computing grid is built in the spanwise direction using a large number of cell layers. The finite width in the spanwise direction is 1 cm for the global wing section. To improve the representation of the turbulent kinetic energy (TKE) at the high-lift configuration, the grid has been hand adapted in the necessary zones such that physical effects like unsteady pressure fluctuations, flow interlocking, and accelerations with the possible and required accuracy are reproduced. At this point, it should be noted that in particular laminar/turbulent transition effects, such as Tollmien–Schlichting waves, the flow separation, reattachment, or cross-flow transition cannot be exactly represented using a fully turbulent flow model alone. It is also suggested that three-dimensional turbulence effects, such as turbulent eddy topologies in the form of hairpins, strips, or streaks, are described and calculated with at least a quasi–three-dimensional simulation model. For this purpose, it is necessary; however, that the computational model be constructed with a large number of layers (32, 40, or 64) in the spanwise direction. A numerical simulation of quasi– three-dimensional models requires high-performance computers, which can provide huge data storage and enormous computing power.
From our experience, we know that the aerodynamic noise propagation is emitted at both the upper and lower trailing edges of the slat and at the trailing edge of the flap of the entire high-lift system. This is known to be an important issue in the analysis of the global airframe noise and is the reason why obtaining an exact solution in the numerical CFD/CAA investigation is quite difficult. In this study, high-precision numerical simulations on a three-element high-lift configuration with a sweep angle are explored. The main objective is to provide a validated numerical prediction tool that allows the identification of the dominant noise source mechanisms, and therefore, the development of a physical concept to reduce or damp the acoustic farfield noise. In this context, numerical simulations are a useful tool for exploring the aerodynamic efficiency and aeroacoustic noise propagation of an aircraft structure. Hybrid aerodynamic and aeroacoustic noise propagation calculations of modern high-lift devices are particularly regarded as useful tools, because it is difficult to obtain reasonable measurements such as windtunnel- specific sensitivities in terms of the Reynolds number; so-called three-dimensional large-scale effects are even observed with nominal two-dimensional simplified bodies.
The free-field simulation is carried out under the landing approach conditions. The atmospheric parameters required are listed in Table 3.
The following calculations for the high-lift configuration are carried out with these aerodynamic state variables.
The free-field simulation serves as a reference of the wind tunnel investigations. The objective of the investigations is to simulate a freeflight configuration with a constant sweep angle of Λ=30° under an effective angle of attack of αeff=4.28°. The wind tunnel measurements must accordingly be carried out to fulfil the aerodynamic conditions of the free-field simulation.
The quasi–two-dimensional model with a periodic boundary condition at the left and right spanwise faces is adjusted. For the wing and flaps, the viscous wall boundary condition is defined. At the inflow and outflow part of the grid, the farfield boundary condition is applied. The distance of the farfield from the leading edge of the main wing is 30 chord lengths. The mesh has only one grid cell in the spanwise direction with a width of w=1 cm.
Figure 6 shows the geometric location of the flow probes (microphones) around the high-lift configuration and the DLR F15-wing with 1 m and 2 m radii around the computational origin, respectively. The origin of the computational grid is located at leading edge of the main wing.
In addition to the microphone probes shown at the high-lift device, more fluidic probes are defined in the slat cove and behind the upper slat trailing edge wake area.
Figure 6 shows the zoomed-in details of the computational grid around the slat of the high-lift configuration in the landing-phase. The slat/main wing leading edge domain was refined with triangular cells locally with cylindrical geometrical sources to better resolve the viscous large-eddy structures, gap flow characteristics between the slat and main wing, local oscillating wake vortex streets, and pressure fluctuations due to strong gradients at the lower trailing edge of the slat, to mention a few of them. The boundary layer region around the aerofoil is modelled with 30 layers of quad cells to improve the computational description of the velocity profile and to guarantee a necessary dimensionless wall distance y+<1.0.
In the Table 4, the typical necessary input parameters for generating the geometrical mesh of the boundary layer around the slat and main wing, such as the thickness of the first cell heights, the number quadslayers, and the stretch factor of the quads layer, are listed.
The following Table 5 provides information regarding the number of points and elements used for the numerical examination (Figure 7).
| Number of points | 1213696 |
| Number of prisms | 900968 |
| Number of hexahedra | 153450 |
| Number of triangles | 1801936 |
| Number of quadrilaterals | 312740 |
Table 5: Hybrid grid information.
The generation of the hybrid, unstructured computational grid was performed using CENTAUR.
Table 6 summarizes the combined variables of the characteristic flow condition for a wing in the landing approach with a velocity of v=55.0 m/s.
| Mach number | 0.1603 | - |
| Flight velocity | 55.0 | m/s |
| Reference length | 1.2 | m |
| Adiabatic exponent | 1.41 | - |
| Specific gas constant | 287.0 | J /(kg K) |
| Static temperature | 293.15 | K |
| Static pressure | 101325 | Pa |
| Total temperature | 294.560 | K |
| Total pressure | 103159 | Pa |
| Dynamic pressure | 18228.4 | Pa |
| Density | 1.20494 | kg/m3 |
| Speed of sound | 343.114 | m/s |
| Dynamic viscosity | 1.81325e-05 | Pa·s |
| Reynolds number | 4.3858e+06 | - |
Table 6: Flight condition in landing approach.
The angle of attack for the conducted computations is set to α=4.28°.
The time-step size for unsteady iterative, implicit GS calculation is defined as Δt=1.0e-05 s. For the GS-scheme, three iterations are considered.
The generation of slat noise at a high-lift device represents a complex aeroacoustic problem, which consists of broadband noise and roughly short pressure-signal interference. Here, individual aerodynamic and/ or aeroacoustic resonances are evoked as studied by Khorrami [1].
Figure 8 schematically outlines the physical flow characteristics for a slat of a high-lift configuration. The uninterrupted free flow streams to the trailing edges of the slat. At the slats’ lower trailing edge, strong flow gradients are produced, which are caused by the immense difference of pressure between the free-flow region and the recirculation zone on the inner side of the slats’ bay. Furthermore, corner-induced flow separations build small-scale vortexes at this point, which emanate from the sharp corner of the lower trailing edge of the slat.
The slat flow splits in an unsteady vortex flow and a shear layer flow, which accelerates in direction of the trailing edge.
Along the turbulent separation line, which divides the recirculation zone and the free-flow region, a turbulent separation layer is produced and fed continuously with vortex energy by free-stream flow and is thus steadily accelerated (Figure 8).
The small-scale turbulent vortex structures produce tonal backcoupling effects there. As this is a subsonic flow, the oscillating acoustic wave moves in the upstream direction along the upper slat wall back to the stagnation point of the slat to create unsteady oscillations. Beyond the gap between the slat and main wing, the flow is divided into an unsteady turbulent wake flow and a turbulent boundary layer created at the main wing, which is accelerated in the downstream direction on the suction side of the main wing as studied by Khorrami [1].
We observe the following turbulent mechanisms:
I. Pressure instability created in consequence of the recirculation vortex in the slat cove.
II. Turbulent shear layer continuously fed with vortex energy.
III. Turbulent structures are impinging at the slats’ inner solid wall.
IV. Acceleration of turbulence spots is passing the slats’ upper trailing edge.
V. Tonal effects generated from acoustic back coupling.
VI. High-pressure gradients produce edge diffraction oscillations at the lower trailing edge of the slat.
VII. Oscillating stagnation point generated by upstream back coupling.
Furthermore, a so-called ‘cavity noise’ produces tonal effects like ‘Rossiter Modes’ Hein [59], which are identified at the beginning of the turbulent shear layer. The turbulence spots merge and swirl along the separation line, which splits the recirculation area from the free-stream flow region.
The listed mechanisms are reproduced well in detail in the numerical simulation (Figures 9 and 10).
In Figure 9, we show the convergence history of the steady simulation. Here the global force coefficients, such as the lift, drag, and y+ coefficients, which represent the dimensionless wall distance, are obtained over a number of steady iterations. The simulation demonstrates a stable, robust, and converged solution. Table 7 summarizes the global calculated forces such as the lift-, drag-, and yaw momentum coefficients.
| Flow coefficient | Steady flow |
|---|---|
| Lift (CLift) | 1.633 |
| Drag (CDrag) | 0.0388 |
| Y-momentum (CMy) | -0.300 |
Table 7: Global force coefficient for a steady aerodynamic flow simulation.
The farfield of the computational grid is located at approximately 30 m from the main wing’s leading edge of the high-lift configuration; this is 30 aerofoil lengths (Figure 9).
The turbulent kinetic energy (TKE) around the slat cove region of the landing device is shown for the grid depicted in Figure 10. The building process of the TKE is kindled at the sharp corner of the lower trailing edge of the slat and the mixing of the high-gradient flow that can be observed. The separation line indicates the transition from the recirculation region in the slat cove to the free undisturbed flow, which can be clearly identified. As a result of the swirling rotation from the pressure fluctuations that ‘swim’ along the separation line, tonal effects are produced when the turbulent eddies impinge at the lower slats’ wall. These turbulent spots increasingly accelerate on the trace of the separation line, because they are continually fed by the energy of the free undisturbed flow
Comparing the turbulent kinetic energy as result from isotropic k-ω SST turbulence model on the right, with the TKE generated from anisotropic Reynolds stress model – we have no production of kinetic energy in isotropic k-ω SST model. So a fundamental answer is found for our investigation: turbulent kinetic energy is modelled only by using anisotropic tensor Reynolds stress model.
The geometric location of the cut A-A in the slat cove is shown in Figure 10. Along this cut A-A, Figure 11 shows the TKE. Owing to the surface skin-friction effects on the inner wall of the slat, the TKE increases slightly, and the TKE in the vortex core of the slat cove reduces to the minimum. Along the separation line, the oscillating pressure fluctuations are moving in consequence of the flow mixing and the pressure compensation from the free-stream flow and slat railing edge vortexes, which cover large turbulent energy values. The recirculation zone is bounded very sharply at the separation line and builds the transition to the free-stream flow field. A steep drop in the TKE value to zero is directly observed at the separation line into the free-stream flow. For the x-axis, a normalized distance coordinate is defined, where the origin is placed on the slat, and the separation line is located at 1.0.
Figure 11 shows a comparison of the Mach number along the cut A-A (Figure 10) in this work. The representation shows a comparison between a hot wire measurement (black points), an LES conducted at RWTH Aachen (green curve), and the current code FPS-AEOLus (red curve), all of which were published in Kolb [60]. Both simulations are in good agreement with the PIV measurement except at locations close to the wall, where surface friction is dominant. The PIV measurements have been performed in the Aeroacoustic Wind Tunnel Braunschweig (AWB) of the Institute of Aerodynamics and Flow Technology. The AWB enables the measurement of flow fields with very low noise production in terms of its sources and the radiation in the aerodynamically induced noise [61].
The distribution of the Mach number around the slat domain is presented in Figure 12. Here, the flow mixtures and retention effects at the wing stagnation point as well as a fluidic convolution due to a velocity increase in the slat/wing channel can be observed. At the vortex rim of the slats bay, we observe a Mach number fluctuation along the free boundary of the recirculation zone (separation line). Eddy water can be identified at the lower bottom zone in the slat cove. In the wake region of the slat, we observe shear flow effects because of the upper slat flow and the gap flow built by the lower slat flow and main wing boundary layer. Strong flow acceleration is observed around the main wing nose, and the flow is forced to flow through the slats/main wing gap.
The pressure distribution around the slat cove is shown in Figures 13 and 14. The emergence of the pressure fluctuations at the sharp lower corner of the slat is predicted well. The core of the vortex can be exactly determined. A slight damping of the pressure can be identified on the upper, inner slat wall. This blockage prevents a better airflow of particles through the slat/wing gap and is cited as one of the main causes of the wing noise as studied by Khorrami [1]. A transition area is described along the separation line, where the local pressure fits the pressure dominating in the free-stream region. At the stagnation points of the slat and the main wing, we observe a high-pressure area (shown in red colour). Over the upper main wing, we observe a strong suction zone.
In Figure 13, the eddy-viscosity distribution in the slat cove is depicted. We see a slight increase in the eddy-viscosity in the outer area of the slat cove vortex of the recirculation zone and a higher concentration of the eddy-viscosity due to the impinging of the vortex bubbles at the inner slat wall and gap flow acceleration.
Figure 14 illustrations the cp - distribution of the high-lift configuration on the slats, the main wing, and the landing flap. The measurement in the DNW is marked with black dots. In general, a good agreement can be found between measurement and the simulation with FPS-AEOLus (red curve). At the suction side of the main wing, the simulation shows lower values. However, from our experience we know that the effective angle of attack of the high-lift device depends on the distance of the farfield. In the present version, the distance of the farfield is approximately 15 chord widths of the wing. The cp -distribution on the slat, the flap, and on the pressure side of the wing is in excellent agreement with the measurement, but there exist small deviations at the front upper side (Figure 15).
The different properties of flow vortexes can be used for the local identification of vortex cores. A local minimum of pressure marks the centre of a vortex; however, a vortex does not necessarily exist if a minimum is observed in the pressure field. Time-dependent strains can also cause a pressure minimum in the flow field, which has nothing to do with a rotation or swirl in the fluid vortex structures. Moreover, viscous effects can cause the minimum pressure to disappear even though a vortex exists in the flow field.
The definition of vortex strength in that context is not clearly suitable, since zones of large shear stresses also lead to high values of vortex strength.
For the local grid adaptation or modern DES-methods for modelling of the complex blending functions and even for the postprocessing visualization of the simulated flow field, the introduced vortex detection criteria are used, such as the Q-criterion of Hunt, Wray and Moin [67]. The derivation of the Q-criterion is as follows:
frequently applied vortex detection criterion is the Q-criterion, which sets the rotation rate Ωij and the shear rate tensor Sijin the relationship. Herein, Q is the second scalar invariant of the velocity derivative tensor. We thus obtain equation (46) as follows.
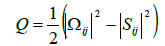 (46)
(46)
Where 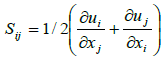 , which is the shear-rate tensor, and
, which is the shear-rate tensor, and 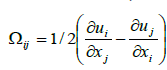 , which is the rotation-rate tensor.
, which is the rotation-rate tensor.
The application of the Q-criterion defined in equation (46) is shown in Figures 6‑12. The Q-criterion describes the changes in the velocity and swirling flow. Here, flow accelerations are drawn in red and decelerations or blockages around the stagnation points are highlighted in blue, both of which are easy to identify. Along the separation line, the flow passes from the free-stream field and slows down owing to the recirculation in the slat cove. The viscosity produces a slightly fannedout pattern. On the upper side of the slat and main wing, we observe the growth of the boundary layer (red areas) (Figure 16).
The calculated pressure fluctuation at an arbitrary physical time ‘t’ of the unsteady flow simulation is visualized in next (Figure 17). Huge flow gradients produce turbulence spots at the lower trailing edge of the slat, which run along the separation line and split the recirculation zone in the slat cove from the free-stream flow under the main wing nose area. The turbulence spots impinge at the lower inner wall of the slat and are reflected to the upper nose of the main wing.
The Mach number distribution at an arbitrary physical time‘t’ is shown in Figure 18. A strong mixing process can be observed on the upper trailing edge of the slat. Here, the shear flow and the gap flow from the pressure side of the slat area cause strong wave interferences and mixing processes with the growing boundary layer of the main wing in the wake region of the slat. The simulated, unsteady results show an oscillation of the slats’ stagnation point induced from acoustic back-coupling effects. The acoustic back coupling rotates in the counter-clockwise direction around the slat domain.
The runtime-averaged states are provided within the unsteady simulation process; therefore, the temporal states are summed up and are divided by the number of timesteps.
For a High-Lift device in landing approach, the slat noise is the main component of the total airframe noise for a civil aircraft, and hence this is a significant contributor to overall aircraft noise in the landing condition. Combined CFD/CAA methods seem to be effective to reduce slat noise, but the decrease in aerodynamic performance, such as maximum lift coefficient, stall angle, etc. were also accompanied, since they change the geometries to reduce noise, which in turn will ruin aerodynamic performance. The unbalanced reduction in aerodynamic efficiency is not acceptable when the application to an existent aircraft is considered, even if it is an effective way to reduce noise. Controlling slat noise without adversely affecting the aerodynamics of the High- Lift device has proved more challenging. A comparison of the acoustic pressure fluctuation in the slat cove area at the same physical time t is depicting in the following Figure 19. Therefor the LE-fluctuation is generated by the NS-input fluctuation and applying a combined Momentum-Lamb vector source model. In the left sketch the Navier- Stokes pressure fluctuation is shown, it serves as input to calculate LEfluctuations outlined in the right. The LE-fluctuation (left) compared to the NS-fluctuation are a bit more detailed. The general physical mechanism like back scattering effects, which produce stagnation point oscillations at the slat and main wing are given (Figure 20).
The results presented involve quasi–two-dimensional simulations to approximately simulate cross-flow effects. Therefore, the computational grid built in the spanwise direction has one cell layer. The finite spanwise width is w=1 cm with a constant sweep angle of Λ=30° along this wing section. To model the physical cross-flow effects that are caused by the geometrical sweep angle Λ of the wing, a periodic boundary condition is introduced at the spanwise side walls.
To improve the representation of the TKE for the high-lift configuration, the computational grid in zones of expected high gradients around the slat, main wing, and the landing flap is resolved finer, in order that the physical effects such as the generation of unsteady pressure fluctuations and flow interlocking, impingements, decelerations, and accelerations are modelled with the required accuracy. As concluded in the results section before, as a central answer of the investigation – the modelling of turbulent kinetic energy can be produced by anisotropic Reynolds stress model in tensor form.
It should be mentioned at this point that the typical unsteady flow effects of a high-lift configuration are predicted with the chosen HARLS method, which is based on a seven-equations SSG/LRR-ω Reynolds stress turbulence model, to predict the rough vortex structure in addition to both MDDES and SAS correction techniques. The generation of pressure fluctuations from AHRLS in the slat cove of the high-lift system is well predicted. In addition, small turbulence structures that arise due to strong flow gradients at the lower corner of the slat and move continuously along the separation line are in close alignment of the description from studies of Khorrami [1]. These small turbulence spots are stimulated from the highly energetic freestream and continuously fed. The impingement of the turbulence spots at the inner side of the high-lift slat is also well predicted. Just, both mechanisms designate the natural noise sources in the slat cove region. The comparisons performed between LE- and NS-fluctuations for the CFD/CAA prediction are in a good agreement.
To assess the achieved numerical results quantitatively much better – experimental, unsteady Particle Image Velocimetry data (uPIV) gained from wind tunnel measurements would be very helpful, also to improve the tuning of the sophisticated turbulence model.
With respect to future investigations and complex transition mechanisms, such as Tollmien–Schlichting waves, the treatment of flow separation and reattachment must be undertaken. For this purpose, advanced transition models derived for finite volume approaches could be used. This multifaceted type of flow cannot be modelled by fully turbulent approaches; however, it plays an important role in the laminar– turbulent global aircraft design.
In this context, it remains to be determined if it is possible to calculate and predict three-dimensional turbulence effects such as turbulent eddies in the form of hairpins, stripes, and streaks using only quasi–three-dimensional simulations. Furthermore, it may be also recommended that micro-turbulences are investigated more precisely using the new synthetic eddy method SEM, e.g. Jarrin [68]. For this purpose, it is necessary, however, that the computational model in the spanwise direction is built up in a number of layers (40, 64, or 128). Such simulations are very expensive in computational time and memory storage. For this type of application, a minimum of 500 cores are necessary using demanding high-performance super-computer systems.