Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
+44-77-2385-9429
ISSN: 2168-9792
+44-77-2385-9429
Research Article - (2012) Volume 1, Issue 1
The heading sensitive drift of inertial platform system changes with the degradation of components’ performance and the coupling characteristics under long-term storage conditions. Such heading sensitive drift is different from the drift under working conditions, and it is difficult to analyze its stability for allocating resources for the calibration and maintenance in engineering application. In this paper, firstly the theory and expression of heading sensitive drift caused by servo loop zero and structure disturbing torque was presented and derived. Secondly, the drift characteristic of influence parameters was analyzed thoroughly based on the expression, and the integrated behavioral model of heading sensitive drift under servo loop zero and disturbing torque influence was concluded. And then, the long-time drift characteristic, acceleration performance and stability of heading sensitive drift behavior were analyzed with actual storage condition profile. The results indicate that heading sensitive drift on the X, Y and Z axis has the similar long-term drift characteristics without acceleration response, which is different from the response characteristic in actual use and therefore has great significance for allocating resources for the calibration and maintenance in inertial platform system.
<Keywords: Long-term storage; Heading sensitive drift behavioral; Servo loop zero; Structure disturbing torque
Heading sensitive drift mainly refers to the phenomenon of output of Gyro drifts along with the heading attitude change of inertial platform system, and its value is more than ten times or even scores of times of Gyro precision level with unpredictable drift status, which is a difficult issue for the research of inertial platform system precision nowadays [1-3].
The influence mechanism of heading sensitive drift is complicated and inter-correlated, and its influencing factors are generally summed up into the following four: servo loop zero and structure disturbing torque, vibration, temperature and magnetic influence. Currently, researches in this regard mainly focus on the transient response of heading sensitive drift, and compensation design for the using precision of heading sensitive drift is conducted accordingly [4-7].
For the missile inertial platform system which has the characteristic of long-term storage and onetime usage, many factors including bearing stiffness changing, materials creep, lubrication damping degradation and so on have great influence on the heading sensitive drift behavior under long-term storage conditions, and as their influence mechanism is complicated and inter-correlated [8-10], it brings great difficulty for the calibration and maintenance of the inertial platform system heading sensitive drift. Therefore, the research of inertial platform system heading sensitive drift storage stability is very significant for allocating resources for the calibration and maintenance. The results indicate that heading sensitive drift on the X, Y and Z axis has the similar long-term drift characteristics without acceleration response, which is different from the response characteristic in actual use and therefore has great significance for allocating resources for the calibration and maintenance in inertial platform system.
Research object
Figure 1 is the frame structure of inertial platform system - the research object of this paper, which is mainly composed of azimuth ring, pitch ring, rolling ring and other connection structure, and provides the pitch angle, the roll angle and the azimuth angle measurements needed by missile attitude control for the device through attitude angle sensor on the gimbal axis [11].
Figure 1: Frame structure of inertial platform system.
Under the long-term storage conditions, servo loop zero and structure disturbing torque of inertial platform system in Figure 1 will change with the materials creep or heading attitude angle drift, which makes the gyros output additional angle related to the heading attitude angle drift [12].
The principle of heading sensitive drift caused by servo loop zero and structure disturbing torque
Inertial platform system isolate the angle movement by the three servo loops of the azimuth ring, the pitch ring and rolling ring, so as to maintain the stability and tracking of the inertial platform structure. With comprehensive analysis, the detailed block diagram of the rolling ring and pitch ring’s servo loops of vertical gyros is shown in Figure 2, and the detailed block diagram of the servo loop and its self-locking loop of traverse gyro is shown in Figure 3 [6,7,13].
Figure 2: Detailed block diagram of the servo loop of vertical gyros rolling ring and pitch ring.
Figure 3: Detailed block diagram of the servo loop of traverse gyros azimuth ring and its self-locking loop.
It can be concluded from Figure 2 and Figure 3 that the heading sensitive drift caused by servo loop zero is as follow:
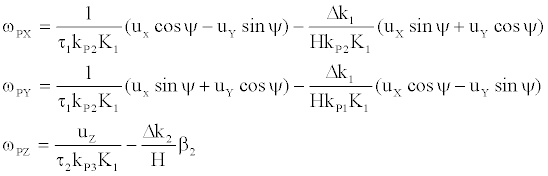(1)
The heading sensitive drift caused by structure disturbing torque is as follow:
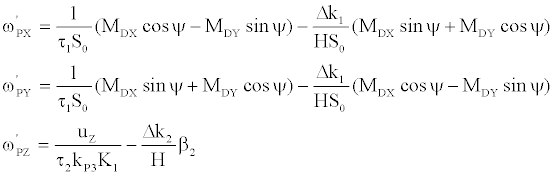(2)
Where, τ1, τ2 are the time constants of vertical gyro and traverse gyro; K1 is the scale factor of the preamplifier, H is the gyro angular momentum; S0 is the stiffness coefficient of the servo loop; MDX, MDY, MDZ are the structure disturbing torque from the pitch axis, rolling axis and azimuth axis of the inertial platform system respectively; uX, uY, uZ are the servo loop zero from pitch servo loop, rolling servo loop and azimuth servo loop of the inertial platform system respectively; kP1, kP2, kP3 are the sensor scale coefficients of vertical gyro’s X axis and Y axis and traverse gyro’s Y axis; β2 is the drift angle of traverse gyro rotor rolling around the Y axis and X axis, Δk1, Δk2 are the residual elastic coefficients of vertical gyro and traverse gyro respectively; λ1, λ2 are the orthogonal damping elasticity coefficients of vertical gyro and traverse gyro; ψ is the heading angle.
Engineering experience has shown that servo loop zero mainly refers to AC interference in demodulator input terminal and input zero of DC amplifier, both of which can be analyzed by converting into the input of demodulator, meanwhile, the disturbing torque taking effect on the gimbal axis mainly refers to the bearing friction torque [1,14]. Therefore, this section deeply analyzed the creep mechanism and behavior characteristic of demodulator input zero and bearing friction torque, analyzed the behavioral characteristics of model parameters in equations (1) and (2), and then comprehensively derived the heading sensitive drift behavioral model of inertial platform system.
Drift behavior of servo loop zero
In inertial platform system, the drift mechanism of servo loop zero in servo loop shown in figure 4 (use the pitch servo loop and rolling servo loop for examples).
Figure 4: The produce mechanism of servo loop zero.
Wang Fang et al. [14] pointed out that servo loop zero will change with temperature and ux, uy, uz mainly refer to 19.2 KHz AC interferences in demodulator input terminal and input zero of DC amplifier, which are analog circuit parameters and their performance depends on the creep characteristic of the resistor, the capacitor and the amplifier. The paper analyzed the degradation features of preamplifier in servo loop by experiment, and then got the drift behavioral model of servo loop zero with the initial value uX = uY = uZ = 10mV = 0.01V as follow:
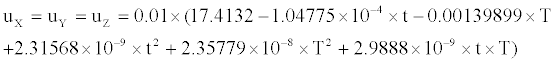(3)
Drift behavior of bearing friction torque
Bearing friction torque means all kinds of damping torque related to bearing rotating, which not only involves bearing structure, dimensions, materials, heat treatment performance, but is also influenced by the working load, lubrication situation and environment, and all those factors interact and interfere with each other, which makes the research even more complicated [10-12].
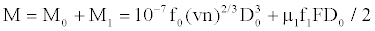(4)
Where: M0 is the bearing friction torque without loads (N•mm); M1 is the bearing friction torque caused by loads (N•mm); f0 means the bushes type and lubrication type; v is the lubrication coefficient of lubricant base oil under the operating temperature (mm2/s); n is the bearing speed (r/ min); D0 = (d+D)/2 is the bearing average diameter (mm), among d is the bearing’s inner diameter, D is the bearing’s outer diameter; μ is the friction coefficient; f1 is the factor reflecting the load direction; F is the bearing load (N), , Fr is the bearing’s radial load (N)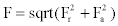 
, Fa is the bearing’s axial load (N).
The parameter data in Table 1 is the roller bearing structure parameter value used in certain inertial platform system.
Under the long-term storage conditions, lubrication coefficient and friction coefficient have the creep feature, which exert a tremendous influence on the bearing friction torque.
Creep law of lubrication coefficient: Under the storage condition, bearing in inertial platform system cannot add any extra lubricant, but meanwhile it has to be made sure that there is no lubricant starvation or lubricant accumulation. Therefore, the creep will occur to the lubricant coefficient under the impact of factors like time or temperature during the storage, which will result in changes of the bearing friction torque.
Based on Hagen-Poiseuille’s law of capillary viscosity measurements, we obtained the lubrication coefficient creep model of certain lubricating oil within different storage temperature rang (20°C~70°C) along with the time shown as follow:
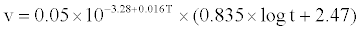(5)
Creep law of friction coefficient: The combined influence of the over surplus assembly, micro components on the material surface and the surface roughness in bearing structure makes the bearing friction coefficient drift mechanism complicated and difficult to figure out.
With the axial and radial loads as shown in Table 1, the creep model of roller bearing friction coefficient of certain inertial platform system drift along with temperature and time can be concluded as follow:
| Parameters | value |
|---|---|
| average speed n(r/min) | 5 |
| bearing’s inner diameter d/mm | 60 |
| bearing’s outer diameter D/mm | 95 |
| axial load N | 150 |
| Radial load N | 180 |
| f0 | 6 |
| f1 | 5×10-4 |
Table 1: Parameters of certain sealed spherical roller bearing
μ = 0.0135ln(t) + 0.1273 (6)
Combine equation (4), (5), (6) and the data in Table 1, the drift mechanism model of the bearing friction coefficient can be concluded as follow:
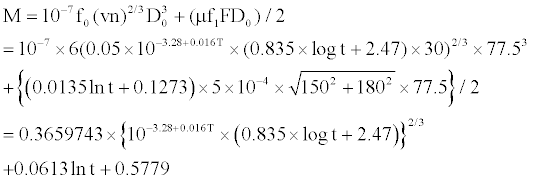(7)
Analysis of heading sensitive drift model parameter drift behavior
Heading sensitive drift expression caused by servo loop zero and structure disturbing torque is related to the preamplifier scale factor K1, sensor scale factors kp1,kp2, gyro angular momentum H, gyro time constant τ, residual elastic coefficient Δk, drift angle of traverse gyro rotor Y axis and X axis β2 and servo loop stiffness S0,the paper studied there parameters respectively.
Scale factor of preamplifier: The degradation rule of the preamplifier is similar to that of the resistor and capacitor, and according to the acceleration characteristic of analog electronic products, we choose the Arrhenius as the preamplifier behavior model, which suitable for mainly affected by temperature situation [18].
Through the experiment analysis of preamplifier’s key resistor drift characteristic, we can get the preamplifier behavior model with the initial value K1 = 50 as follow:
K1=50×(17.4132-1.04775×10-4×t-0.00139899×T +2.31568×10-9×t2+2.35779×10-8×T2+2.9888×10-9×t×T) (8)
Scale factor of sensor: Sensor, which takes many forms, is a measuring system composed of sensitive components and measuring circuit, and the sensor used in dynamically tuned gyro is variable reluctance inductive sensor [19].
The derivation expression of variable reluctance inductive sensor is as follow [13]:
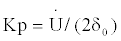(9)
Where, Kp is the scale factor of sensor, δ0 is the initial clearance between iron core and magnetic conductance ring, Δδ = ra, r is the center diameter of the sensor’s iron core, and a is the rotating angle of gyro rotor.
Engineering experience has proved that the drift of sensor scale factor is mainly caused by the clearance change between iron core and magnetic conductance ring, and also the center diameter parameter drift of the sensor’s iron core, Such change or drift is mainly influenced by the thermal expansion coefficient under the working of temperature, however, the thermal expansion coefficient does not have temperature acceleration characteristic. Therefore, constant design value of the sensor’s scale factor is set at kP1=kP2=2.5mV/arc minute.
Gyro angular momentum: The expression of gyro angular momentum is as follows [13]:
H=Jzω (10)
Where, JZ is the polar axis rotational inertia of the gyroscope rotor; ω = πf/30 is the rotation angular speed of the gyroscope rotor, rad/s; f is the speed of the gyroscope rotor, r/min.
We can conclude from the above that gyro angular momentum mainly depends on its design value and is not influenced by the temperature or the time. Therefore, we set the initial value at H = 74.088kg•m2/h here in this paper.
Gyro time constant: The computational expression of gyro time constant is as follow [13]:
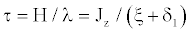(11)
Where, JZ is the polar axis rotational inertia of the gyroscope rotor, ξ is the damping coefficient of the rotor gas, δ1 is the internal friction damping coefficient of the flexible hinge, and λ is the orthogonal elastic damping coefficient.
From the description of the above parameters, it can easily concluded that gyro time constant is mainly influenced by material damping, and the we can use the drift rule of material’s damping coefficient degradation to reflect the degradation characteristic of the gyro time constant. Based on the concept of equivalent viscous damping, the paper converts the gyro damping into viscous damping (the conversion method is to deem that viscous damping consumes the same energy with other viscous damping in a vibration period), and take it as the acceleration coefficient of the gyro time constant. Ultimately, the behavior model of gyro time constant with an initial value τ1 = 1/60h of in certain inertial platform system is as follow:
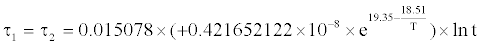(12)
Residual elastic coefficient: The definition of residual elastic coefficient is as follow [13]:
Δk = K0 = (a+b-c)N2/2 (13)
Where, K0=(a+b-c)N2/2 is the rigidity elastic coefficient of gyro, a, b and c are the rotational inertia around X axis Y axis and Z axis of middle gimbals ring respectively, N is spin velocity of gyro, and N0 is the tuning speed of gyro under the tuned state.
Generally, after the flexible support structure parameters are determined, the parameters that can be adjusted are only the rotational inertia a, b, and c and rotating speed N. Therefore, the drift of residual elastic coefficient is only related to the stiffness characteristic of bearing material. The paper makes experimental analysis of the material stiffness characteristic of dynamically tuned gyro and concludes the drift behavior model of residual elastic coefficient as follow:
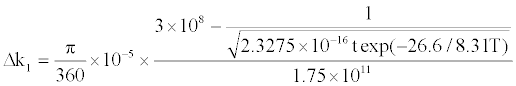(14)
Drift angle of azimuth gyro around X axis: The X axis of azimuth gyro connected to inertial platform structure by the self-locking loop, and thus β2 only depends on the loop zero and its output of the selflocking loop, which do not change with heading angle. The functional block diagram of gyro X axis’ work on the servo loop is shown in Figure 5 [13].
Figure 5: The functional block diagram of gyro X axis works on servo loop.
Gyro sensor converts the rotate angle of the X axis into electrical signal and transmits it into the lock-in amplifier, which then supplies the gyro torque with current proportionate to the electrical signal, and finally the gyro torque produces moment to enable the rotation of gyro until the gyro H axis is brought to zero.
Therefore, the behavior characteristic of the drift angle of azimuth gyro around X axis is the same with the servo loop zero in terms of behavior. The drift behavior model of the drift angle of the azimuth gyro around X axis with an initial value β2=1.5×10-6rad = (270/π)×10-6°can be concluded according to equation (3) below:
β2 = (270/π)×10-6×(17.4132-1.04775×10-4×t-0.00139899×T +2.31568×10-9×t2+2.35779×10-8×T2+2.9888×10-9×t×T) (15)
Stiffness of servo loop: The principle of servo loop stiffness is as follow [20]:
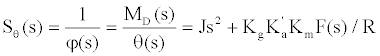(16)
Where, Kg=H/C, and C is the viscous damping coefficient, Km is the motor torque coefficient, R is the total resistance of torque motor,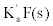
is the transfer function of servo amplifier,
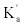is the total magnification of servo amplifier, F(s) is the network transfer function, and J is the total moment inertia of the torque motor around output shaft.
From the above analysis, it can be seen that the acceleration of the servo loop stiffness depends on the performance of the servo loop, and thus has the same degradation characteristic with the servo loop. By referring to equation (3) above, the drift behavior model of servo loop stiffness with an initial value of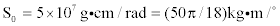 
can be concluded as follows:
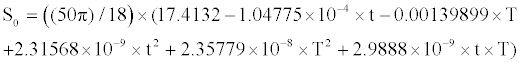(17)
Drift behavioral model for the heading sensitive drift of inertial platform system
Inserting equations (3) ~ (17) into equation (1) and (2) , i.e. heading sensitive drift caused by servo loop zero and structure disturbing torque respectively, we can easily get the synthetical drift behavioral model with MX0=MY0=Mz0 and unified parameters unit. In order to analyze the model in a more vivid and effective way, this paper applies the response surface identification method to rewrite the mechanism equation (1) and (2), which results in equation (18) as below:
ωX = ωPX+ ω’PX = 0.013528735853104 - 1.0606312285 x 10-5g - 5.537104156 x 10-6 T - 4.23727461 x 10-7 t +1.759374 x 10-9 g x T + 7.6329 X 10-11g x t +2.6142 x 10-11 T x t +3.84714339 x 10-7 g2 + 5.438001 x 10-9 T2 + 1.2679 x10-11 t2 + 0.901256402152763 - 8.33169068108 x 10-4g - 4.40627696664 x 10-4 T + 5.279128685 X 10-6 t +1.47853436 x 10-7 g x T - 1.651471 x 10-9 g x t -5.43285 x 10-10 T x t +3.3436136318 x 10-5 g2+ 4.70814861 x 10-7 T2 - 8.9493 x 10-11 t2
ωY - ωPY + ω’PY - 0.013527824455615 - 1.060631872 x 10-5 g -5.532447054 x 10-6 T - 4.23704875 x 10-7 t + 1.759392 x 10-9 g x T + 7.6329 x 10-11 g x t + 2.6095 x 10-11 T x t + 3.84714273 x 10-7 g2 + 5.432393 x 10-9 T2 + 1.2678 x 10-111 t2 + 0.901184717331631 - 8.3316907565 x 10-4 g - 4.4025611517 x 10-4 T + 5.280729664 x 10-6 t + 1.47853481 x 10-7 g x T - 1.651471 x 10-9 g x t - 5.46192 x 10-10 T x t + 3.3436136301 x 10-5 g2 + 4.70355533 x 10-7 T2 + 8.9514 x 10-11 t2
ωZ - ωPZ + ω’PZ - 0.013528314450239 - 1.0606338982 x 10-5 g - 5.534950528 x 10-6 T - 4.23717017 x 10-7 t + 1.759454 x 10-9 g x T + 7.6329 x 10-11 g x t +2.612x 10-11 T x t + 3.84714404 x 10-7 g2 + 5.435407 x 10-9 T2 + 1.2679 X 10-11 t2 + 0.901220595325726 - 8.33169101491 x 10-4 g - 4.40442088735 x 10-4 T + 5.279928327 x 10-6 t + 1.47853563 x 10-7 g x T – 1.651471 x 10-9 g x t – 5.44737 x 10-10 T x t +3.3436136534 x 10-5 g2 + 4.70585418 x 10-7 T2 - 8.9503 x 10-11 t2
Analysis of Inertial Platform System Heading Sensitive Drift Behavior under Storage Condition
Simulating the equation (18) by Matlab with the heading angle set at zero, the paper gets the data of inertial platform system heading drift in ten years under different temperature and the results are shown in Table 2.
| Drift time/year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| X axis heading sensitive drift(°/h) | 20° | 0.0182546 | 0.0178035 | 0.0175922 | 0.0174423 | 0.0173068 | 0.0171677 | 0.0170170 | 0.0168512 | 0.0166694 | 0.0164718 |
| 40° | 0.0181831 | 0.0177338 | 0.0175234 | 0.0173741 | 0.0172391 | 0.0171005 | 0.0169503 | 0.0167851 | 0.0166039 | 0.0164071 | |
| 60° | 0.0181206 | 0.0176730 | 0.0174633 | . 0173145 | 0.0171799 | 0.0170418 | 0.0168920 | 0.0167274 | 0.0165468 | 0.0163505 | |
| 80° | 0.0180657 | 0.0176195 | 0.0174104 | 0.0172620 | 0.0171279 | 0.0169901 | 0.0168408 | 0.0166766 | 0.0164964 | 0.0163007 | |
| 100° | 0.0180170 | 0.0175720 | 0.0173636 | 0.0172156 | 0.0170818 | 0.0169443 | 0.0167953 | 0.0166315 | 0.0164518 | 0.0162565 | |
| Y axis heading sensitive drift(°/h) | 20° | 0.0182546 | 0.0178036 | 0.0175923 | 0.0174424 | 0.0173069 | 0.0171678 | 0.0170171 | 0.0168513 | 0.0166695 | 0.0164719 |
| 40° | 0.0181832 | 0.0177339 | 0.0175235 | 0.0173742 | 0.0172392 | 0.0171006 | 0.0169504 | 0.0167852 | 0.0166041 | 0.0164072 | |
| 60° | 0.0181207 | 0.0176731 | 0.0174634 | 0.0173146 | 0.0171801 | 0.0170419 | 0.0168922 | 0.0167275 | 0.0164965 | 0.0163008 | |
| 80° | 0.0180658 | 0.0176196 | 0.0174105 | 0.0172622 | 0.0171280 | 0.0169902 | 0.0168409 | 0.0166767 | 0.0164965 | 0.0163008 | |
| 100° | 0.0180171 | 0.0175722 | 0.0173637 | 0.0172157 | 0.0170819 | 0.0169444 | 0.0167954 | 0.0166316 | 0.0164519 | 0.0162566 | |
| Z axis heading sensitive drift(°/h) | 20° | 0.0182546 | 0.0178035 | 0.0175922 | 0.0174423 | 0.0173069 | 0.0171677 | 0.0170170 | 0.0168513 | 0.0166694 | 0.0164719 |
| 40° | 0.0181831 | 0.0177339 | 0.0175234 | 0.0173741 | 0.0172391 | 0.0171005 | 0.0169503 | 0.0167852 | 0.0166040 | 0.0164071 | |
| 60° | 0.0181207 | 0.0176731 | 0.0174633 | 0.0173145 | 0.0171800 | 0.0170418 | 0.0168921 | 0.0167274 | 0.0165468 | 0.0163505 | |
| 80° | 0.0180657 | 0.0176195 | 0.0174105 | 0.0172621 | 0.0171279 | 0.0169901 | 0.0168408 | 0.0166766 | 0.0164965 | 0.0163007 | |
| 100° | 0.0180170 | 0.0175721 | 0.0173636 | 0.0172156 | 0.0170818 | 0.0169443 | 0.0167954 | 0.0166315 | 0.0164518 | 0.0162565 |
Table 2: Behavioral data of inertial platform system heading sensitive drift in storage condition.
Fitting the data in Table 2, we can get the drift curve shown as Figure 6-8.
Figure 6: Drift law of inertial platform system heading sensitive drift on X-axis.
Figure 7: Drift law of inertial platform system heading sensitive drift on Y-axis.
Figure 8: Drift law of inertial platform system heading sensitive drift on Z-axis.
Long-term drift characteristic analysis: From Figure 6-8, it can be easily found that heading sensitive drift has similar drift characteristic on X, Y and Z axis under long-term storage conditions, and this phenomenon is different from that under the operating conditions, as under operating conditions, drift on X axis and Y axis is larger than that on Z axis [1].
Acceleration feature analysis: From Figure 8-10, it can be easily found that the temperature change has little influence on the heading sensitive drift, but the drift is obvious under the long-term working of temperature, which means the temperature has no acceleration feature with the heading sensitive drift caused by servo loop zero and structure disturbing torque.
Figure 9: drift curve of heading sensitive drift stability.
Storage stability analysis: The average storage temperature in the warehouse is 20°C, a storage cycle is to calibrate the heading sensitive drift every 12 months, the calibration temperature is 70°C, and the time of calibration is 48 hours. The paper simulates the accumulative drift value after every cycle and analyzes its storage stability with the result shown in Table 3.
| Storage period | X axis stability | Y axis stability | Y axis stability |
|---|---|---|---|
| 1 year | 0.14304378 | 0.142997679 | 0.143023471 |
| 2 years | 0.143492198 | 0.143446075 | 0.143471879 |
| 3 years | 0.143702901 | 0.14365677 | 0.143682578 |
| 4 years | 0.14385262 | 0.143806484 | 0.143832295 |
| 5 years | 0.143988075 | 0.143941935 | 0.143967748 |
| 6 years | 0.143993762 | 0.143946623 | 0.143972435 |
| 7 years | 0.144002423 | 0.143956285 | 0.143982097 |
| 8 years | 0.14401845 | 0.143972313 | 0.143998125 |
| 9 years | 0.144034531 | 0.143988394 | 0.144014205 |
| 10 years | 0.144050275 | 0.144004138 | 0.144029949 |
Table 3: Analysis result of storage stability of inertial platform system heading sensitive drift.
Fit the stability data on X axis, Y axis and Z axis in Table 3 and we can get the curve drawn as Figure 9.
From Table 3 and Figure 9, we can find that without regard to the influence of vibration, temperature and magnetic field, the storage stability of heading sensitive drift caused by servo loop zero and structure disturbing torque can meet the requirement of the stability for one year in current engineering, that is, 0.2°C/h (which means the biggest drift difference ≤ 0.2°C/h), however, the stability value still contributes a lot to the whole drift. Therefore, the optimization of resource calibration and maintenance is still of great concern for the heading sensitive drift.
In this paper, the principle of inertial platform system heading sensitive drift caused by servo loop zero and structure disturbing torque is comprehensively analyzed and discussed and the parameters characteristic of heading sensitive drift behavioral model is derived with experiment measurement. Finally, the behavioral model of heading sensitive drift is summarized and the storage stability is analyzed under actual storage environmental profile. The research approach and conclusion are meaningful not only to theoretical research but also engineering application. The major contribution and innovative points are as follow:
(1) The bearing stiffness drift, material creep and lubrication damping characteristics are considered in the heading sensitive drift research under long-term storage condition for the first time, which has provided theoretical support for the heading sensitive drift behavioral analysis of inertial platform system with the feature of “long-term storage and one time using”.
(2) Through deep analysis of the mechanism of bearing friction torque and behavioral of heading sensitive drift model parameters, the paper has deduced the behavioral model of inertial platform system’s heading sensitive drift, and has vividly presented the long-term drift behavioral performance along with temperature and time by system identification method.
(3) Through the analysis of heading sensitive drift’s storage behavioral, the paper concludes that the heading sensitive drift caused by servo loop zero and structure disturbing torque does not have acceleration feature, and the stability drift value, while meeting the requirement of long-term stability, still contribute a lot to the whole system’s drift. The conclusion and finding is of great significance for guiding the resources allocation for the calibration and maintenance in inertial platform system.