Journal of Aeronautics & Aerospace Engineering
Open Access

Placing the spacetime interval on a fourth spatial dimension which is conjugate to mass

Johan Kirsten^{* *}Correspondence: Johan Kirsten, Department of Aeronautical Engineering, University of Cape Town, Cape Town, South Africa, Email:

Author info »

Introduction

These three assumptions connect concepts in general relativity and quantum mechanics. From these assumptions a relativistic Lagrangian is derived, containing the electromagnetic potentials. This relativistic Lagrangian is applied to some simple examples to show the results are consistent with what we already know.

A testable prediction is also provided that can be investigated by experiment. This experiment is very important, as it has never been done and could prove that space-time is not curved as hypothesized by general relativity.

From this work the paper draws the following conclusions:

•A non-inertial frame of reference has a changing c' over space and/or time and an inertial frame of reference has constant c'; and
•Spacetime is not curved but flat and it is the gradient in c' that creates the illusion of curved spacetime; and
•The gravitational force and electromagnetic force are both due to potentials that have their origin in the same an action field; and
•There is a negative time gradient in c’ that explains the cosmological redshift, implying a static universe.

This work and these conclusions, might possibly create a context from which further work might be done to explain hitherto unexplained phenomena. If this work agrees with observation, it implies we should reconsider the concept of curved spacetime. Developing the ability to control c’ might give us the ability to develop highly advanced propulsion technology [1,2].

Literature Review

Motivating a variable speed of light

The first to propose that the speed of light might be variable was Einstein who said [3] 'From the proposition which has just been proved, that the velocity of light in the gravitational field is a function of the place, we may easily infer, by means of Huygens's principle, that light-rays propagated across a gravitational field undergo deflexion'. This has been further investigated by Dicke, Broekaert and Unzicker and Preuss among others [4-6]. So, what does an observer, external to a gravity well, think the speed of light is inside the gravity well? A thought experiment can be used to prove that the speed of light is lower inside the gravity well [7].

It is well known that time dilation occurs inside the gravity well. So, according to the observer outside the gravity well, the light takes a longer time to travel the same distance while inside the gravity well. Therefore, according to the outside observer, the speed of light inside the gravity well is slower.

So, either our measurement of space and time imply changes in space and time, depending on conditions. Or our measurement tool, the speed of light, changes to give the illusion of changes in space and time.

Discussion

Velocities from the Minkowski metric

The spacetime interval is defined by:

Distance in three-dimensional space is defined using:

Distance in four-dimensional space is defined using:

The mapping of time onto three-dimensional space is defined as:

The mapping of time onto four-dimen

sional space is defined as:

The mapping of time onto the fourth spatial dimension is defines as:

This gives:

Dividing by c² and using the definition of g gives:

If the coordinate time derivative is applied to Equation 7 and assuming c is constant, this gives:

Deriving a relativistic Lagrangian

Define action S as,

Where ψ is a unitless scalar field over five-dimensional space. Define energy, momentum and mass as

The Lagrangian is therefore:

Which can be expanded to:

Using the definition of mass m and c’ gives

From the definitions of energy and momentum, it is clear the second and third terms are energy and momentum fields. These terms do not have a charge vector as the first term does with m. To turn these terms into potentials with a charge vector, a new scalar field is introduced: ψ_p. This scalar field is also defined over five-dimensional space and has the unit of 1/C.

Introducing this new field into Equation 16 gives:

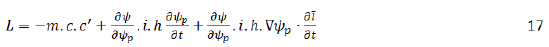
Defining,

gives:

The first term can be converted from using m to E, using Equation 8, as follows:

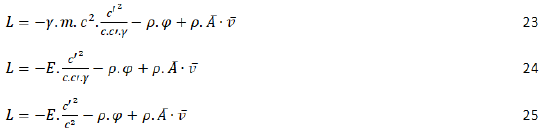
Deriving the electromagnetic potential equations

Using the definition of mass, changes the Klein-Gordon Equation to:

Which is a homogenous wave Equation travelling in time of four spatial dimensions, with the wave in the fourth spatial dimension determining the mass. The same can be done for the Dirac Equation.

Assuming the ψ_p field also has homogenous wave equations in four dimensions gives:

Successively applying time and spatial gradient and using the definitions of Ψ and Ā gives:

To derive the electromagnetic potential equations requires

Similarly, it requires:

Multiplying Equation 31 and Equation 35 gives:

Which is true for matter waves with v=v_g

This implies Equation 28 and 29 gives:

Which is the electromagnetic potential equations.

To derive the continuity Equation, apply the second order derivative with respect to the fourth spatial dimension to the Lorenz condition:

Applying the relativistic Lagrangian

In this section, the relativistic Lagrangian will be applied to a few examples. Assuming no free charge or current in these examples, gives:

Example 1

A stationary mass is in a weak gravity field. Therefore, v is zero, and c’ can be derived from the Schwarzchild metric:

Where:

Dividing by dt and using the definition of c’ gives

Applying Lagrangian mechanics to the Lagrangian of Equation 45 gives:

For small r_s/r this can be approximated to:

Defining the gravitational acceleration as

Gives,

Example 2

A mass moving at constant non-relativistic velocity, but not in a gravitational field.

From the Equation 8:

Substituting this into Equation 45 gives,

Which can be understood as the kinetic energy and the potential energy due to the rest mass.

Example 3

A mass moving at constant non-relativistic speed in a weak gravitational field.

For this example, the Equation for c’ will be created from a combination of Equation 48 and Equation 57:

Substituting this into the relativistic Lagrangian of Equation 45 and following similar steps gives:

The last term is the gravitational potential. Equation 45 can now be used in Lagrangian mechanics to obtain the gravitational force.

Example 4

Light passing through a weak gravitational field.

For this example, the Equation used for c’ is:

Substituting this into the relativistic Lagrangian of Equation 25 that uses energy:

Gives:

Applying Lagrangian mechanics gives:

And

Therefore

Which can be approximated as

This implies the force on the photon is approximately the Newtonian gravitational force on the effective rest mass of the photon implied by its energy.

Speed of light, c’ and v

From this work massive particles can be modelled as waves in four spatial dimensions, where the velocity in three-dimensional space is v and the velocity in the fourth spatial dimension is c’. This can even be applied to the electromagnetic fields of these massive particles. The speed used for the waves in the potential equations in Equation 28 and 29 is c, but the fields in threedimensional space would propagate at v and the field in the fourth spatial dimension would propagate at c’.

It is a bit more complicated for photons. For a photon the energy-momentum Equation is

The Equation for momentum is

Assuming that the speed of light is c’, the photons rest mass, m, is zero and combining Equation 8, 75, 76 yields.

This can be interpreted to mean the massless photon has an equivalent mass, m^*, of E/c². This makes sense when applied to Equation 48, which would imply that photons have zero speed at a black hole’s event horizon.

It would also make sense for gravitational redshift. As a photon falls into a gravitational field, which has a gradient for c’ in the radial direction, the spatial component of the photon will adjust for the changing c’. As c’ decreases, the wave number k should increase to compensate. This would increase the momentum of the photon and register as a blue shift. If the photon exits the gravity well, its c’ will increase and the wave number will decrease leading to a decreased momentum and a red shift.

What isn’t clear from this, is why light would travel at the speed defined for the fourth spatial dimension? It begs the question, are photons even travelling in 3-dimensional space?

Cosmological red shift

The first to propose a static universe considering a variable speed of light was Dicke. This work shows a slightly different interpretation. Assuming a static universe, it would not be space that is expanding, but light that is travelling from a certain starting point in the history of the universe. This would expose more and more of the universe as time goes on.

It would also mean that more and more of the universe acts gravitationally on light travelling through the universe. Effectively the universe itself is in a gravity well due to all the mass. The gravitational effect due to all the mass in the visible universe would be the same in all directions, but as the universe that is visible expands this effect would increase.

This means that c’ would not have a spatial gradient due to all the mass, but it would have a negative time gradient. As it is a time gradient, the time component of the photon will adjust to the decreasing c’, resulting in a decreased frequency. This would explain the cosmological redshift observed.

This is like the hypothesis proposed by Zwicky in 1929 to account for the cosmological redshift, but without the problems associated with the original proposal.

Testable prediction

It is possible to make a testable prediction from this work. What is clear from the examples and from Equation 9 is that there is a difference between a frame of reference in a gravitational field and a frame of reference that is under acceleration. If a frame of reference is under acceleration, Equation 9 applies and c’ has a gradient in time. If a frame of reference is under gravitational influence c’ has a spatial gradient. Under a spatial gradient in c’, the speed of light is different at different spatial locations. This can be used to design a test of the theory and a test of whether the frame of reference is exposed to a gravitational field or not.

Gravitational frame of reference

In a frame of reference that is subject to a gravitational field, c’ should have a spatial gradient. Such a spatial gradient in c’ can be measured and is not predicted by general relativity. A possible method to do this measurement, is to construct an interferometer with paths of equal length.

In this experiment the light from a source is split in two. The one path is reflected to a higher level and made to follow a horizontal path on a laser test bench. The other path is reflected to a lower level and made to follow a horizontal path on a similar laser test bench. The two light paths are then redirected to the original level and combined to measure the relative phase difference. Laser ranging is used to ensure the two laser test benches are equally far apart from the level the source is on.

Aspects that can affect the phase, apart from a difference in the speed of light, is the gravitational redshift and the curvature of space. If the path lengths are much longer than the hight difference between the laser test benches, these effects should be negligible in comparison to the signal the experiment is looking for.

If this theory is correct, such a device should measure a phase change from between the light in the higher path and the light in the lower path. Such a phase difference should also increase as the difference in height between the two laser test benches is increased. If such a phase change is present, general relativity would not be able to explain it.

In general, such an interferometer subjected to a non-inertial frame of reference where the acceleration has a gradient should measure different light speeds on different axis. Therefore, it should be possible to use such an interferometer on three axis and compare the phase change to determine if acceleration is present in any direction.

At present it does not seem that this experiment has been done. As this experiment holds the possibility to challenge the assumption that the speed of light is invariant, it could have far ranged consequences in physics.

Conclusion

The paper started with making three assumptions that introduced a fourth spatial dimension and connected concepts from general relativity and quantum mechanics.

Using these assumptions, the following conclusions are drawn:

• A non-inertial frame of reference has a changing c' over space and/or time and an inertial frame of reference has constant c'.
• Spacetime is not curved but flat and it is the gradient in c' that creates the illusion of curved spacetime.
• The gravitational force and electromagnetic force are both due to potentials that have their origin in the same an action field.
• There is a negative time gradient in c' that explains the cosmological redshift, implying a static universe.

Apart from these direct conclusions, it is also possible to consider the impact of technology that controlling c' can give.

Future Work

The next step for the theory is to move it to classical field theory and from there to quantize it into a quantum field theory. The theory should also be applied to all the existing observations that confirm general relativity. It should also be applied to current unexplained phenomena such as dark matter. Other existing observations in cosmology should also be investigated using this theory.

References

1. Kaluza T. On the unity problem of physics. Proceedings of the Royal Prussian Academy of Sciences, Berlin. 1921:966-972.

   [Google Scholar]

2. Ingraham RL. Particle masses and the fifth dimension. arXiv preprint hep-th/0005118. 2000.

   [Google Scholar]

3. Einstein A. On the influence of gravitation on the propagation of light. Ann Phys. 1911;35(898-908):906.

   [Google Scholar]

4. Dicke RH. Gravitation without a principle of equivalence. Rev Mod Phys. 1957;29(3):363.

   [Crossref] [Google Scholar]

5. Broekaert J. A spatially-VSL gravity model with 1-PN limit of GRT. Found Phys. 2008;38:409-435.

   [Crossref] [Google Scholar]

6. Unzicker A, Preuss J. A machian version of Einstein's variable speed of light theory. arXiv preprint arXiv:1503.06763. 2015.

   [Crossref] [Google Scholar]

7. Zwicky F. On the redshift of spectral lines through interstellar space. Proc Natl Acad Sci. 1929;15(10):773-779.

   [Crossref] [Google Scholar] [PubMed]