Drug Designing: Open Access
Open Access
ISSN: 2169-0138
ISSN: 2169-0138
Research Article - (2014) Volume 3, Issue 3
In clinical development, a two-stage design combining two separate studies (e.g., a phase II dose finding study and a phase III confirmatory study) into a single trial is commonly considered. The purpose of a two-stage design is not only to reduce lead time between the two studies, but also to evaluate the treatment effect in a more efficient way. In practice, one of the difficulties in utilizing a two-stage design is that the study endpoints at different stages may be different. For example, a biomarker (or the same study endpoint with different duration) may be considered at the first stage, while a regular study endpoint is used at the second stage. As per the studies the case where both study endpoints are continuous variables with certain correlation structure. In this paper, our attention is on the case where the study endpoints are count data which are obtained at the two stages with different time intervals. Statistical procedure for combining data observed from the two different stages are proposed. Furthermore, results on hypotheses testing and sample size calculation are derived for the comparison of two treatments based on data observed from a two-stage design.
<Keywords: Biomarker, Count data, Sample size determination, Twostage design, Weibull distribution
In recent years, the use of a two-stage adaptive seamless design that combines a phase IIb study and a phase III study into a single study has received much attention [1-4]. The purpose of a two-stage adaptive seamless design is not only to accelerate drug development but also to evaluate the treatment in a more efficient way. The major characteristics of a two-stage adaptive phase II/III design include (i) it is able to address study objectives of individual phase IIb and phase III studies and (ii) it utilizes data collected from both phase IIb and phase III studies for a combined final analysis. The efficiency of a two stage design, however, has been challenged by some researchers [5]. Moreover, it is not clear how the final combined analysis should be performed if the study objectives and/or study endpoints are similar but different at different phases [6].
In practice, a two-stage design is often applied to combine a phase IIb dose finding study and a phase III efficacy confirmatory trial. Thus, the study objectives at different stages are different (i.e., dose selection versus efficacy confirmation). Moreover, to speed up the drug development, the study endpoints at different stages may be different. For example, a biomarker may be considered at the first stage and a regular study endpoint is used at the second stage provided that the biomarker is predictive of the regular study endpoint. In these cases, the validity of the standard test statistics for combining data collected from both phases is questionable. In particular, this will have an impact on the sample size allocation in order to achieve the desired power at a pre-specified level of significance at each stage
In general, there may be four different scenarios for a two-stage adaptive seamless design. In particular, in the two stages, (i) the study objectives and the study endpoints are the same; (ii) the study objectives are the same but the study endpoints are different; (iii) the study objectives are different but the study endpoints are the same; (iv) the study objectives and the study endpoints are different. Certainly, these different cases are formulated for different purposes. For instance, case (iii) is often set up for dose finding in the first stage and efficacy confirmation in the second stage. Study with biomarker or clinical endpoint with different durations at the two stages while the objective is for dose selection in the first stage but efficacy confirmation in the second stage would lead to the scenario described in case (iv).
Under the similar setting, Chow et al. [6] proposed a test statistic utilizing data collected from both phases assuming that there is a wellestablished relationship between the two different study endpoints and derived formulas for sample size calculation/allocation based on the proposed test statistic. However, in many clinical studies, it may not be feasible to monitor the patients continuously. For example, the number of subjects “survived” or “onset of a disease” out of the n test subjects at the end of the study period is observed instead of recording the exact time. In other words, the exact time where the event occurred after a treatment is administered cannot be observed. Thus, the main theme of this paper is to develop testing procedures for the comparison of the effects of different treatments based on event data collected from two stages. In particular, we assume that the durations of the two stages are different. The second stage is with duration L whilst the duration of the first stage is cL with 0
In this paper, we propose an improved test statistic under a Weibull distribution based on the location parameter of median. In the next section, the proposed method for combining data observed from two different stages is described. Results for the hypotheses testing of equality, superiority, non-inferiority and equivalence of two treatments are presented in the Section: Hypothesis Testing. Section: Sample Size Calculation gives results for the sample size calculation for achieving a desired power corresponding to each of the hypotheses considered in the section Hypothesis Testing. Section: Numerical Study gives the results of a numerical study. A brief concluding remark is given in the last section.
Consider a two-stage adaptive seamless design for comparing two treatments, namely, a test treatment versus a control agent. Suppose that the study duration of the 1st stage is cL and the study duration of the 2nd stage is L with c<1. Assume that the response is determined by the lifetime t, and the corresponding lifetime distribution function for the test treatment and the control agent are G1(t,θ1) and G2(t,θ2), respectively. Suppose that a respondent is defined as an individual with survival time larger than the study duration. Let r1 and s1 be the numbers of respondents out of n1 and m1 randomly selected individuals in the first and second stages for the test treatment respectively. Similarly, r2 and s2 are the numbers of respondents out of n2 and m2 individuals in the first and second stages for the control treatment respectively.
Based on the observed data, the likelihood functions for the test and control treatments can be obtained as follows
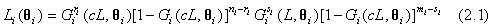
for i=1, 2; where i=1 represents the test treatment and i=2 represents the control treatment. Assume that the lifetimes under the test and control treatments are both Weibull distributed. Denote by G(t;λ,β) the cumulative distribution function of a Weibull distribution with λ,β>0 then, 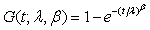 In particular, for i=1, 2, Gi (t;θi)=G(t;λi,βi) and the likelihood functions become
In particular, for i=1, 2, Gi (t;θi)=G(t;λi,βi) and the likelihood functions become
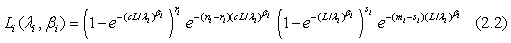
The maximum likelihood estimators (MLE) of λi and βi can be found by solving the following equations 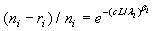 and
and 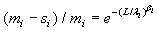 , which are obtained by setting the first order partial derivatives with respect to the parameters to zero. In particular, the MLEs of and are given as βi and λi , are given as
, which are obtained by setting the first order partial derivatives with respect to the parameters to zero. In particular, the MLEs of and are given as βi and λi , are given as
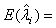 (2.3)
(2.3)
and
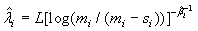 (2.4)
(2.4)
Note that the MLEs of λi and βi exists only when 0 < ri /ni< si /mi<1.
The expectations of 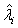 and
and 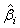 are obtained based on normal approximation of (ni - ri )/ni and (mi - si )/mi for sufficiently large ni and mi. In particular,
are obtained based on normal approximation of (ni - ri )/ni and (mi - si )/mi for sufficiently large ni and mi. In particular,
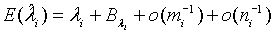 (2.5)
(2.5)
and
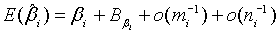 (2.6)
(2.6)
where
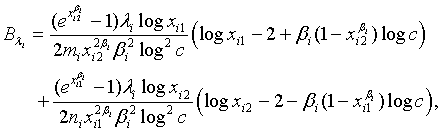
and
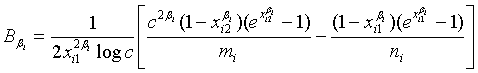
with xi1 = cL /λi and xi2 = L /λi, i =1, 2. Note that for sufficiently large mi and ni, both 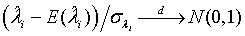 and
and 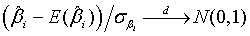 ,where
,where 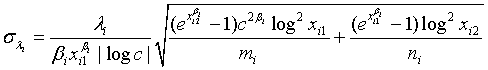 and
and 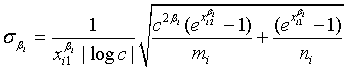
Using the invariance property of maximum likelihood estimation, the MLE 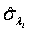 and
and 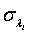 can be obtained by substituting λi and βi with their corresponding MLEs,
can be obtained by substituting λi and βi with their corresponding MLEs, 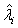 and
and 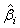 respectively. Similarly,
respectively. Similarly, 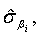
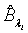 and
and 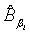 are defined accordingly. Using normal approximation,
are defined accordingly. Using normal approximation, 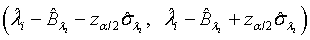 and
and 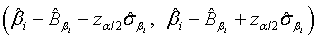 are approximate 100(1-α)% confidence intervals of λi and βi where
are approximate 100(1-α)% confidence intervals of λi and βi where 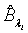 and
and 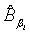 may be omitted when ni and mi are large enough.
may be omitted when ni and mi are large enough.
In pharmaceutical applications, it is usually of interest to estimate the median lifetime. Thus, the comparison of the control and test treatments is usually based on the medians of the corresponding lifetime distributions. In particular, let M be the median of a Weibull distribution, which is given as λ(log2)1/β . The following sections discuss the results for the testing of equality, superiority, non-inferiority and equivalence between the medians of the control and test treatments.
Test for equality
For the testing of equality, the hypotheses are formulated as
H0 :M1 = M2 vs H1: M1≠ M2 , (3.1)
where Mi, i=1, 2 is the median of the lifetime distribution of the test and control treatment respectively. Denote the MLE of Mi by 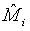 . Applying Taylor series expansion, it can be showed that
. Applying Taylor series expansion, it can be showed that 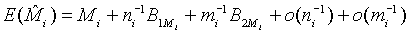 , for i=1, 2, where
, for i=1, 2, where
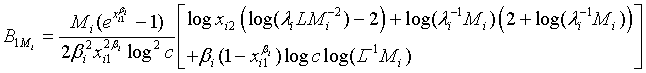
and
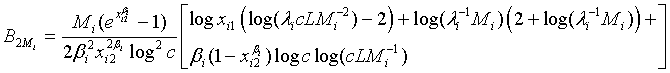
Based on the asymptotic normality of 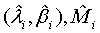 can be approximated by a normal distribution for sufficiently large ni and mi. In particular,
can be approximated by a normal distribution for sufficiently large ni and mi. In particular,
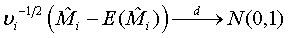 (3.2)
(3.2)
where
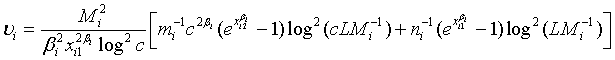
Note that 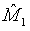 and
and 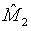 are independent. Thus,
are independent. Thus, 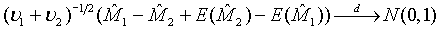 (3.3)
(3.3)
Let 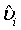 be the MLE of υi , which is obtained by estimating λi and βi with the corresponding MLE, for i=1, 2. Similarly,
be the MLE of υi , which is obtained by estimating λi and βi with the corresponding MLE, for i=1, 2. Similarly, 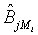 is the MLE of BjMi , i=1, 2, j=1, 2. Then, according to the Slutsky’s Theorem, (3.2) also holds if i υ is replaced by
is the MLE of BjMi , i=1, 2, j=1, 2. Then, according to the Slutsky’s Theorem, (3.2) also holds if i υ is replaced by 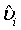 . Consequently,
. Consequently, 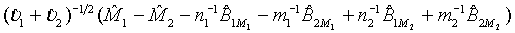 asymptotically follows the standard normal distribution under the null hypothesis H0 defined in (3.1). Thus, the null hypothesis H0 is rejected at an approximate α level of significance if
asymptotically follows the standard normal distribution under the null hypothesis H0 defined in (3.1). Thus, the null hypothesis H0 is rejected at an approximate α level of significance if
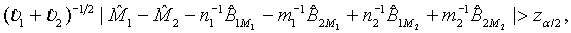
where zα is the 100×(1−α)th-percentile of the standard normal distribution.
Test for superiority
The following hypotheses are considered to identify superiority of the test treatment over the control,
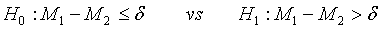 (3.4)
(3.4)
where δ >0 is a difference of clinical importance. Obviously, the null hypothesis should be rejected for large value of 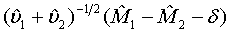 Under the null hypothesis defined in (3.4),
Under the null hypothesis defined in (3.4), 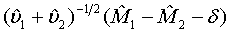 approximately follows a normal distribution for large ni and mi. Thus, the null hypothesis in (3.4) is rejected at an approximate α level of significance if
approximately follows a normal distribution for large ni and mi. Thus, the null hypothesis in (3.4) is rejected at an approximate α level of significance if
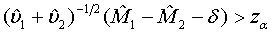 (3.5)
(3.5)
Test for non-inferiority
To show that the test treatment is not worse than the control, the hypotheses H0 :M2 − M1≥δ vs H1:M2−M1 <δ are considered, which are equivalent to
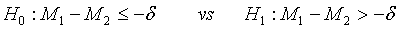 (3.6)
(3.6)
where δ>0 is the difference of clinical importance. The hypotheses in (3.6) are of similar form as those for the testing of superiority in (3.4). Thus, the null hypothesis is rejected at an approximate α level of significance if
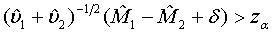 (3.7)
(3.7)
Test for equivalence
In clinical trial, it is commonly unknown whether the performance of test treatment is better than the (active) control, especially when prior knowledge of the test treatment is not available. In this case, it is more appropriate to consider the following hypotheses for therapeutic equivalence:
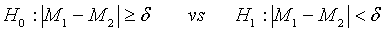 (3.8)
(3.8)
The above hypotheses can be tested by constructing the confidence interval of M1 - M2. Based on Schuirmann (1987) two one-sided tests procedure, it can be verified that the null hypothesis defined in (3.8) is rejected at a significance level α if and only if the 100(1-2α)% confidence interval
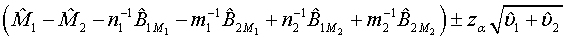
falls within (−δ ,δ ) . In other words, the test treatment is concluded to be equivalent to the control if
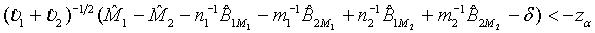 (3.9)
(3.9)
and
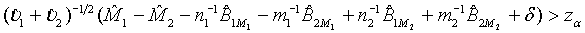 (3.10)
(3.10)
Sample Size Calculation
In this section, the problem of determining the sample size used in each phase is considered. In practice, the total sample size N for the two phases is often determined such that the corresponding statistical test would achieve a given level of power (1-β). Consequently, a related question is how to allocate the samples sizes in the two phases given the total sample size is N. Thus, the corresponding results of sample size determination for each of the four tests discussed in Section: Hypothesis Testing are presented in the following.
To facilitate the understanding of the idea, the problem is restricted to the case of one treatment in order to get some insight for the generalization to the two treatment case. Suppose that the following hypotheses are considered
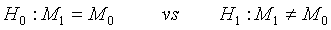 (4.1)
(4.1)
where M0 is a pre-specified value. Based on the asymptotic normality of MLE 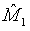 of M1, the null hypothesis H0 defined in (4.1) is rejected at an approximate α level of significance if
of M1, the null hypothesis H0 defined in (4.1) is rejected at an approximate α level of significance if 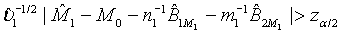 Since
Since 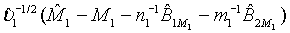 can be approximated by the standard normal distribution, the power of the above test under the alternative hypothesis H1 can be approximated by
can be approximated by the standard normal distribution, the power of the above test under the alternative hypothesis H1 can be approximated by 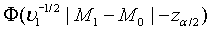 , where Φ is the cumulative function of the standard normal distribution. Hence, in order to achieve a power level of 1−β, the required sample size satisfies
, where Φ is the cumulative function of the standard normal distribution. Hence, in order to achieve a power level of 1−β, the required sample size satisfies 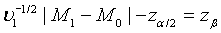 Let m1= ρn1 . Then the required sample size N for the two stages is given by N = (1+ ρ )n with
Let m1= ρn1 . Then the required sample size N for the two stages is given by N = (1+ ρ )n with
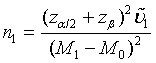 (4.2)
(4.2)
and
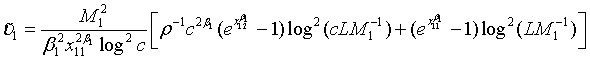 (4.3)
(4.3)
Note that with all the other parameters fixed, the required sample size N is a convex function of ρ and the optimal value of ρ is given as
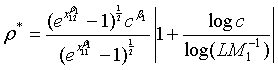 (4.4)
(4.4)
Following the similar idea, the sample size to achieve a pre-specified power of 1-β for the tests discussed in Section: Hypothesis Testing with significance level α can be determined. For testing equality of two treatments based on the comparison of the medians, the required sample size for testing hypotheses (3.1) satisfies the following equation,
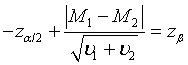
Let m1 = ρn1 , m2 = ξn2 and n2 = γn1. υi can be expressed as 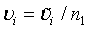 , i = 1, 2; where
, i = 1, 2; where 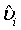 is given in (4.3) and
is given in (4.3) and

The total sample size NT for the two treatment groups is given by n1[1 + ρ (1+ξ )γ] with
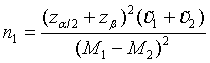 (4.5)
(4.5)
Similarly, for the testing superiority, non-inferiority and equivalence, the corresponding n1 is given as 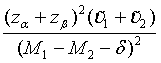 ,
, 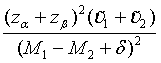 and
and 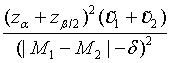 ,respectively.
,respectively.
Numerical Study
Note that the results derived in the above sections are based on asymptotic approximation. Thus, in this section, numerical studies are considered to assess the finite sample performance of these results. In practical applications, one has to know the values of L and c in order to determine the required sample size N. Therefore, one of the objectives of this numerical study aims to provide some insights to determine the “best” L such that the corresponding sample size is minimized. Furthermore, this numerical study also aims to provide some evidence whether the sample size derived based on approximation, as given in Section: Sample Size Calculation, can actually achieve the nominal power level.
It should be noted that the optimal ρ, as given in (4.4), may be very extreme which leads to the sample sizes in the two phases being too unbalanced. To avoid this problem, truncated ρ* is considered which is defined as
 (5.1)
(5.1)
Since N is a convex function of ρ and attains its minimum at ρ*, it is easy to verify that N attains its minimum at ρtr under the condition ρ1 ≤ρ ≤ ρ2 . For demonstration purpose, we choose ρ1 =0.2 and ρ2=5 in this numerical study.
Given α, β, α1, β1 and M0, the required sample size N is a function of ρ, c and L. With ρtr substituted into (4.3), optimal values of c and L can be determined by numerical method. However, since N is a discrete function of c and L, there is a set of optimal values of c and L. In other words, each optimal L is accompanied by a set of optimal c. Thus the best choice of the study duration L is proposed to be the one such that the minimum sample size, say N*, is achieved and this choice of L, denote by L*, is most robust in c, where N* is defined as min N(ρ ,c, L) ρ1 ≤ ρ ≤ ρ2 , c > 0, L > 0 . In our numerical study, the grid search method was used to find L*. Furthermore, set α=0.05, β=0.20 and the difference between M1 and M0 was chosen to be 0.2. Some results are presented in Table 1. It can be seen that L* is roughly equal to the 53rd-pcercentile of the Weibull distribution. In addition, L* is increasing in β1 and λ1 while N* is decreasing in β1 but increasing in λ1.
| β1 | 1 | 1.5 | 2 | 2.5 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λ1 | 1.2 | 1.4 | 1.6 | 1.8 | 1.2 | 1.4 | 1.6 | 1.8 | 1.2 | 1.4 | 1.6 | 1.8 | 1.2 | 1.4 | 1.6 | 1.8 |
| N* | 283 | 385 | 503 | 636 | 161 | 219 | 286 | 361 | 102 | 139 | 182 | 230 | 71 | 96 | 125 | 158 |
| L* | 0.908 | 1.059 | 1.211 | 1.332 | 1.014 | 1.184 | 1.355 | 1.495 | 1.037 | 1.236 | 1.416 | 1.585 | 1.084 | 1.267 | 1.449 | 1.592 |
| L* as quantile | 0.531 | 0.531 | 0.531 | 0.523 | 0.540 | 0.541 | 0.541 | 0.531 | 0.526 | 0.541 | 0.543 | 0.539 | 0.540 | 0.541 | 0.542 | 0.521 |
Table 1: Minimum sample size N* and optimal duration L*.
In addition to the determination of the optimal duration L*, an important issue is to explore the effect of c and deviation of L from its optimal value on the required sample size. To get some insight, a numerical study was conducted with M1 - M0 =0.2 and some selected values of L and c. The corresponding results are presented in Table 2. It can be noted that when L< L*, the sample sizes are very sensitive to the choice of c; whilst N is relatively more robust to the choice of c when L>L*. Thus, the results suggest that a study duration slightly larger than L* should be used when an accurate estimate of L* is not available.
| β1 | 1 | 1.5 | 2 | 2.5 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | 1.2 | 1.4 | 1.6 | 1.8 | 1.2 | 1.4 | 1.6 | 1.8 | 1.2 | 1.4 | 1.6 | 1.8 | 1.2 | 1.4 | 1.6 | 1.8 | |
| L*-0.1 | c=.4 | 371 | 478 | 601 | 792 | 213 | 272 | 341 | 448 | 168 | 185 | 228 | 285 | 113 | 138 | 168 | 236 |
| .5 | 380 | 482 | 600 | 800 | 218 | 275 | 341 | 452 | 177 | 189 | 230 | 287 | 117 | 141 | 171 | 243 | |
| .6 | 394 | 488 | 599 | 811 | 226 | 278 | 341 | 457 | 193 | 195 | 234 | 290 | 124 | 147 | 175 | 255 | |
| .7 | 419 | 499 | 598 | 831 | 240 | 284 | 340 | 466 | 223 | 205 | 239 | 295 | 139 | 159 | 184 | 279 | |
| .8 | 475 | 521 | 595 | 873 | 272 | 297 | 338 | 485 | 294 | 230 | 251 | 305 | 175 | 187 | 204 | 337 | |
| L*-0.05 | c=.4 | 315 | 422 | 544 | 714 | 181 | 241 | 311 | 406 | 129 | 159 | 204 | 258 | 85 | 113 | 144 | 196 |
| .5 | 310 | 413 | 533 | 703 | 178 | 237 | 305 | 400 | 130 | 157 | 201 | 254 | 85 | 112 | 143 | 198 | |
| .6 | 303 | 403 | 520 | 688 | 175 | 232 | 298 | 392 | 132 | 155 | 197 | 250 | 86 | 111 | 141 | 199 | |
| .7 | 294 | 392 | 507 | 669 | 170 | 225 | 290 | 382 | 135 | 151 | 192 | 243 | 86 | 110 | 139 | 202 | |
| .8 | 284 | 386 | 504 | 644 | 164 | 220 | 287 | 367 | 142 | 146 | 185 | 234 | 86 | 108 | 135 | 209 | |
| L* | c=.4 | 292 | 398 | 520 | 670 | 170 | 231 | 301 | 385 | 113 | 151 | 197 | 249 | 78 | 106 | 139 | 178 |
| .5 | 288 | 392 | 512 | 656 | 166 | 226 | 295 | 377 | 110 | 147 | 192 | 243 | 76 | 103 | 135 | 175 | |
| .6 | 286 | 389 | 509 | 643 | 165 | 224 | 292 | 369 | 108 | 144 | 188 | 238 | 74 | 101 | 131 | 172 | |
| .7 | 285 | 388 | 506 | 640 | 163 | 222 | 290 | 366 | 105 | 142 | 186 | 235 | 73 | 99 | 129 | 168 | |
| .8 | 284 | 386 | 505 | 638 | 162 | 220 | 288 | 364 | 103 | 141 | 184 | 232 | 72 | 98 | 127 | 162 | |
| L*+0.05 | c=.4 | 293 | 398 | 519 | 654 | 172 | 234 | 305 | 381 | 112 | 155 | 201 | 252 | 83 | 111 | 145 | 176 |
| .5 | 290 | 394 | 514 | 648 | 169 | 229 | 299 | 375 | 109 | 150 | 195 | 246 | 79 | 107 | 138 | 171 | |
| .6 | 288 | 391 | 510 | 644 | 166 | 226 | 295 | 371 | 107 | 146 | 191 | 240 | 76 | 103 | 134 | 166 | |
| .7 | 286 | 389 | 507 | 641 | 164 | 223 | 291 | 367 | 105 | 144 | 187 | 236 | 74 | 100 | 131 | 164 | |
| .8 | 284 | 387 | 505 | 639 | 162 | 221 | 288 | 364 | 104 | 141 | 184 | 233 | 72 | 98 | 128 | 161 | |
| L*+0.1 | c=.4 | 295 | 401 | 523 | 658 | 176 | 238 | 309 | 387 | 117 | 159 | 207 | 259 | 87 | 117 | 151 | 184 |
| .5 | 292 | 396 | 517 | 651 | 171 | 232 | 302 | 379 | 112 | 153 | 199 | 250 | 82 | 110 | 143 | 176 | |
| .6 | 288 | 392 | 512 | 646 | 167 | 227 | 296 | 373 | 109 | 148 | 193 | 243 | 78 | 105 | 137 | 170 | |
| .7 | 286 | 389 | 508 | 642 | 164 | 224 | 292 | 368 | 106 | 144 | 188 | 238 | 75 | 101 | 132 | 166 | |
| .8 | 286 | 386 | 504 | 639 | 162 | 220 | 288 | 364 | 104 | 141 | 184 | 233 | 72 | 98 | 128 | 162 | |
Table 2: Total sample size N for testing equality using ρtr α=0.05 and 1-β=0.80.
Note that for the four types of comparison, i.e., testing equality, superiority, non-inferiority and equivalence, between the two treatments, the total sample size is dependent on the ratios of sample sizes in the two stages and the two treatments, i.e., ρ, ξ and γ. An interesting question is how to determine the optimal values of these ratios such that the required total sample size NT is minimized. It can be proved that for given c and L, there exist optimal values of ρ, ξ and γ such that the total sample size NT is minimized. This result is true for the four types of comparison. In particular, the optimal values of ρ, ξ and γ are given as
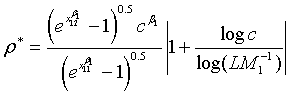 (5.2)
(5.2)
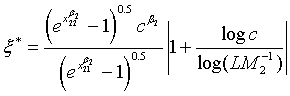 (5.3)
(5.3)
and 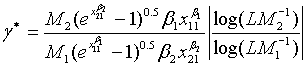 (5.4)
(5.4)
Following the similar idea of avoiding extreme values, let ρtr, ξtr and γtr be the truncated ρ*, ξ* and γ*, respectively, which are defined similarly as ρτρ in (5.1). Then, a grid search method is applied to determine the best duration L* with which the total sample size NT is minimized and NT is most robust to c. In this study, ρτρ, ξtr and γtr are used with the truncated limits chosen as 1 1 1 ρ =ξ =γ = 0.2 and 2 2 2 ρ =ξ =γ = 5. It should be noted that, unlike ρtr in the one treatment case, ρtr, ξtr and γtr may not necessary be the optimal combinations to give the minimum NT. Determination of the required sample size for testing equality of two treatments is considered with α=0.05 and β=0.20. The corresponding optimal durations L* for various combinations of Weibull model parameter values are given in Table 3. Furthermore, a numerical study was conducted to assess the effects of c and the deviation of L from its optimal value L* on the sample size. The results are presented in Table 4. As shown in Table 4, NT is more robust to c when L>L*.
| i. β2=2.0 | ||||||||||||
| λ2 | 1.0 | 1.1 | ||||||||||
| β1 | 1.5 | 2 | 1.5 | 2 | ||||||||
| λ1 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 |
| NT* | 316 | 207 | 151 | 153 | 108 | 82 | 715 | 382 | 247 | 290 | 179 | 125 |
| L* | 1.152 | 1.252 | 1.342 | 1.232 | 1.322 | 1.422 | 1.145 | 1.240 | 1.330 | 1.220 | 1.320 | 1.410 |
| ii. β2=2.5 | ||||||||||||
| λ2 | 1.0 | 1.1 | ||||||||||
| β1 | 1.5 | 2 | 1.5 | 2 | ||||||||
| λ1 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 |
| NT* | 357 | 222 | 157 | 161 | 110 | 82 | 948 | 445 | 270 | 333 | 191 | 129 |
| L* | 1.165 | 1.249 | 1.329 | 1.229 | 1.319 | 1.409 | 1.135 | 1.232 | 1.329 | 1.224 | 1.314 | 1.404 |
Table 3: Minimum sample size NT* and optimal duration L*.
| β2 | 2 | 2.5 | |||||||||||||||||||||||
| 1.0 | 1.1 | 1.0 | 1.1 | ||||||||||||||||||||||
| β1 | 1.5 | 2 | 1.5 | 2 | 1.5 | 2 | 1.5 | 2 | |||||||||||||||||
| L | λ1 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 |
| L*-0.1 | c=.4 | 493 | 341 | 231 | 236 | 155 | 110 | 1066 | 661 | 415 | 425 | 273 | 179 | 640 | 404 | 272 | 260 | 175 | 124 | 1403 | 729 | 499 | 514 | 321 | 205 |
| .5 | 473 | 321 | 215 | 224 | 146 | 102 | 1042 | 619 | 392 | 415 | 259 | 168 | 594 | 388 | 258 | 247 | 166 | 116 | 1397 | 692 | 479 | 497 | 304 | 195 | |
| .6 | 457 | 299 | 197 | 212 | 137 | 98 | 1032 | 580 | 364 | 407 | 244 | 158 | 553 | 363 | 240 | 234 | 155 | 108 | 1423 | 663 | 448 | 482 | 286 | 183 | |
| .7 | 456 | 289 | 213 | 206 | 150 | 124 | 1061 | 551 | 339 | 407 | 231 | 163 | 523 | 333 | 239 | 226 | 156 | 120 | 1522 | 654 | 413 | 476 | 271 | 176 | |
| L*-0.05 | c=.4 | 498 | 296 | 206 | 202 | 137 | 100 | 1320 | 603 | 361 | 420 | 238 | 160 | 592 | 347 | 238 | 233 | 152 | 111 | 2110 | 790 | 430 | 525 | 280 | 181 |
| .5 | 463 | 272 | 188 | 187 | 126 | 91 | 1235 | 558 | 332 | 393 | 220 | 148 | 555 | 322 | 219 | 217 | 140 | 101 | 2043 | 748 | 401 | 496 | 262 | 167 | |
| .6 | 421 | 245 | 172 | 172 | 116 | 89 | 1121 | 505 | 300 | 362 | 202 | 135 | 503 | 291 | 197 | 198 | 127 | 93 | 1898 | 685 | 362 | 456 | 240 | 152 | |
| .7 | 377 | 243 | 195 | 171 | 136 | 122 | 992 | 449 | 282 | 331 | 192 | 148 | 442 | 267 | 199 | 182 | 130 | 108 | 1695 | 605 | 321 | 409 | 215 | 147 | |
| L* | c=.4 | 389 | 237 | 169 | 177 | 122 | 90 | 925 | 460 | 288 | 353 | 207 | 143 | 429 | 265 | 187 | 195 | 131 | 96 | 1377 | 573 | 327 | 412 | 235 | 156 |
| .5 | 357 | 220 | 157 | 165 | 113 | 84 | 851 | 426 | 267 | 330 | 193 | 133 | 395 | 243 | 170 | 179 | 119 | 87 | 1245 | 522 | 299 | 382 | 216 | 142 | |
| .6 | 330 | 208 | 153 | 155 | 109 | 87 | 781 | 397 | 251 | 307 | 182 | 125 | 370 | 226 | 158 | 166 | 110 | 83 | 1120 | 479 | 278 | 355 | 200 | 131 | |
| .7 | 320 | 240 | 204 | 175 | 147 | 134 | 728 | 383 | 267 | 290 | 193 | 157 | 357 | 234 | 183 | 167 | 129 | 112 | 1011 | 449 | 275 | 337 | 193 | 142 | |
| L*+0.05 | c=.4 | 351 | 229 | 165 | 174 | 121 | 91 | 797 | 426 | 273 | 332 | 204 | 141 | 412 | 255 | 178 | 192 | 129 | 95 | 1093 | 512 | 310 | 398 | 228 | 152 |
| .5 | 334 | 217 | 156 | 163 | 113 | 84 | 764 | 407 | 260 | 314 | 192 | 132 | 388 | 238 | 165 | 177 | 118 | 86 | 1032 | 484 | 291 | 372 | 211 | 140 | |
| .6 | 322 | 210 | 158 | 155 | 113 | 93 | 741 | 392 | 250 | 301 | 182 | 128 | 370 | 226 | 159 | 165 | 111 | 85 | 996 | 464 | 277 | 353 | 198 | 130 | |
| .7 | 341 | 265 | 224 | 196 | 164 | 147 | 723 | 398 | 290 | 299 | 212 | 175 | 369 | 252 | 199 | 181 | 143 | 123 | 968 | 449 | 289 | 337 | 204 | 155 | |
| L*+0.1 | c=.4 | 356 | 232 | 167 | 178 | 123 | 92 | 808 | 432 | 277 | 340 | 208 | 143 | 419 | 258 | 180 | 196 | 132 | 96 | 1103 | 520 | 315 | 409 | 233 | 155 |
| .5 | 337 | 218 | 156 | 165 | 113 | 85 | 772 | 410 | 261 | 319 | 194 | 133 | 391 | 240 | 166 | 179 | 119 | 86 | 1045 | 489 | 293 | 378 | 214 | 141 | |
| .6 | 322 | 215 | 165 | 159 | 118 | 99 | 744 | 393 | 252 | 302 | 184 | 132 | 370 | 227 | 162 | 166 | 114 | 89 | 1003 | 465 | 277 | 354 | 199 | 132 | |
| .7 | 373 | 293 | 244 | 221 | 182 | 161 | 727 | 427 | 318 | 321 | 236 | 194 | 392 | 274 | 217 | 200 | 158 | 135 | 968 | 462 | 309 | 347 | 220 | 170 | |
Table 4: Total sample size NT for two treatments with α =0.05 and 1- β =0.80.
Furthermore, a simulation study was conducted to assess the finite sample performance of the results derived in Section: Sample Size Calculation, which are based on asymptotic approximation. The simulated powers are given in Table 5. In this study, the simulated powers are computed based on 10000 simulated trials and the nominal power level is 0.8. Results listed in Table 5 show that the simulated powers are much less than 0.80 in most cases. The results suggested that the approximation results derived in Section: Sample Size Calculation are too conservative, which leads to less power to discriminate the null and alternative hypotheses. However, when sample sizes are increased by 50%, most powers are larger than 0.80, especially for L* + 0.1 or c not greater than 0.60. The results are listed in Table 6. These result provide valuable insights to practitioners to choose a larger L (> L*) and smaller c (<0.60) if possible.
| β2 | 2 | 2.5 | |||||||||||||||||||||||
| λ2 | 1.0 | 1.1 | 1.0 | 1.1 | |||||||||||||||||||||
| β1 | 1.5 | 2 | 1.5 | 2 | 1.5 | 2 | 1.5 | 2 | |||||||||||||||||
| L | λ1 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 |
| L*-0.1 | c=.4 | 0.736 | 0.660 | 0.615 | 0.588 | 0.492 | 0.473 | 0.832 | 0.748 | 0.681 | 0.741 | 0.619 | 0.525 | 0.753 | 0.678 | 0.647 | 0.642 | 0.532 | 0.425 | 0.847 | 0.794 | 0.715 | 0.786 | 0.669 | 0.569 |
| .5 | 0.693 | 0.624 | 0.614 | 0.604 | 0.543 | 0.509 | 0.795 | 0.700 | 0.654 | 0.702 | 0.632 | 0.570 | 0.704 | 0.653 | 0.632 | 0.634 | 0.575 | 0.514 | 0.841 | 0.749 | 0.671 | 0.742 | 0.656 | 0.600 | |
| .6 | 0.632 | 0.626 | 0.599 | 0.606 | 0.573 | 0.515 | 0.743 | 0.652 | 0.617 | 0.651 | 0.610 | 0.579 | 0.652 | 0.623 | 0.636 | 0.615 | 0.601 | 0.529 | 0.805 | 0.689 | 0.628 | 0.679 | 0.620 | 0.608 | |
| .7 | 0.591 | 0.595 | 0.587 | 0.575 | 0.537 | 0.500 | 0.660 | 0.612 | 0.608 | 0.603 | 0.573 | 0.542 | 0.617 | 0.619 | 0.633 | 0.607 | 0.581 | 0.557 | 0.738 | 0.626 | 0.628 | 0.622 | 0.611 | 0.588 | |
| L*-0.05 | c=.4 | 0.714 | 0.672 | 0.629 | 0.606 | 0.485 | 0.419 | 0.795 | 0.733 | 0.684 | 0.704 | 0.621 | 0.529 | 0.739 | 0.681 | 0.644 | 0.610 | 0.524 | 0.387 | 0.822 | 0.764 | 0.705 | 0.750 | 0.649 | 0.577 |
| .5 | 0.676 | 0.644 | 0.622 | 0.607 | 0.549 | 0.486 | 0.760 | 0.685 | 0.650 | 0.688 | 0.623 | 0.569 | 0.688 | 0.650 | 0.626 | 0.622 | 0.575 | 0.484 | 0.810 | 0.711 | 0.673 | 0.712 | 0.644 | 0.586 | |
| .6 | 0.622 | 0.615 | 0.601 | 0.584 | 0.560 | 0.495 | 0.707 | 0.639 | 0.626 | 0.636 | 0.609 | 0.560 | 0.642 | 0.619 | 0.623 | 0.606 | 0.571 | 0.525 | 0.763 | 0.662 | 0.634 | 0.664 | 0.625 | 0.594 | |
| .7 | 0.596 | 0.583 | 0.563 | 0.535 | 0.548 | 0.529 | 0.638 | 0.610 | 0.587 | 0.584 | 0.546 | 0.512 | 0.632 | 0.620 | 0.598 | 0.569 | 0.540 | 0.520 | 0.684 | 0.622 | 0.617 | 0.623 | 0.597 | 0.558 | |
| L* | c=.4 | 0.719 | 0.685 | 0.643 | 0.648 | 0.554 | 0.476 | 0.790 | 0.741 | 0.704 | 0.726 | 0.664 | 0.591 | 0.755 | 0.711 | 0.648 | 0.662 | 0.580 | 0.465 | 0.806 | 0.766 | 0.725 | 0.758 | 0.696 | 0.626 |
| .5 | 0.677 | 0.654 | 0.629 | 0.647 | 0.586 | 0.460 | 0.757 | 0.709 | 0.673 | 0.709 | 0.650 | 0.607 | 0.715 | 0.673 | 0.635 | 0.661 | 0.590 | 0.488 | 0.787 | 0.736 | 0.696 | 0.734 | 0.681 | 0.623 | |
| .6 | 0.643 | 0.588 | 0.567 | 0.591 | 0.532 | 0.444 | 0.723 | 0.656 | 0.629 | 0.662 | 0.615 | 0.574 | 0.683 | 0.637 | 0.578 | 0.634 | 0.535 | 0.428 | 0.748 | 0.693 | 0.649 | 0.705 | 0.645 | 0.577 | |
| .7 | 0.585 | 0.553 | 0.552 | 0.543 | 0.506 | 0.546 | 0.658 | 0.603 | 0.549 | 0.604 | 0.548 | 0.523 | 0.608 | 0.584 | 0.545 | 0.556 | 0.521 | 0.517 | 0.699 | 0.640 | 0.590 | 0.646 | 0.572 | 0.529 | |
| L*+0.05 | c=.4 | 0.759 | 0.709 | 0.687 | 0.710 | 0.649 | 0.534 | 0.779 | 0.758 | 0.731 | 0.760 | 0.726 | 0.681 | 0.764 | 0.731 | 0.679 | 0.736 | 0.643 | 0.520 | 0.785 | 0.765 | 0.741 | 0.777 | 0.744 | 0.683 |
| .5 | 0.725 | 0.682 | 0.633 | 0.679 | 0.612 | 0.470 | 0.766 | 0.718 | 0.701 | 0.735 | 0.703 | 0.655 | 0.749 | 0.704 | 0.642 | 0.709 | 0.618 | 0.476 | 0.778 | 0.749 | 0.714 | 0.763 | 0.723 | 0.672 | |
| .6 | 0.666 | 0.605 | 0.566 | 0.617 | 0.528 | 0.459 | 0.749 | 0.699 | 0.637 | 0.703 | 0.642 | 0.560 | 0.702 | 0.620 | 0.567 | 0.626 | 0.500 | 0.386 | 0.767 | 0.720 | 0.664 | 0.730 | 0.681 | 0.570 | |
| .7 | 0.581 | 0.553 | 0.567 | 0.537 | 0.550 | 0.569 | 0.694 | 0.613 | 0.562 | 0.613 | 0.548 | 0.534 | 0.637 | 0.573 | 0.554 | 0.547 | 0.527 | 0.549 | 0.730 | 0.663 | 0.602 | 0.667 | 0.575 | 0.529 | |
| L*+0.1 | c=.4 | 0.765 | 0.742 | 0.703 | 0.757 | 0.678 | 0.577 | 0.796 | 0.777 | 0.750 | 0.777 | 0.760 | 0.713 | 0.782 | 0.743 | 0.696 | 0.750 | 0.687 | 0.561 | 0.791 | 0.772 | 0.757 | 0.784 | 0.763 | 0.724 |
| .5 | 0.739 | 0.696 | 0.615 | 0.714 | 0.597 | 0.492 | 0.773 | 0.754 | 0.716 | 0.758 | 0.729 | 0.666 | 0.759 | 0.709 | 0.633 | 0.728 | 0.629 | 0.456 | 0.790 | 0.766 | 0.732 | 0.769 | 0.735 | 0.672 | |
| .6 | 0.686 | 0.626 | 0.554 | 0.606 | 0.534 | 0.477 | 0.756 | 0.712 | 0.651 | 0.718 | 0.655 | 0.566 | 0.731 | 0.647 | 0.554 | 0.640 | 0.529 | 0.336 | 0.774 | 0.742 | 0.679 | 0.751 | 0.674 | 0.572 | |
| .7 | 0.594 | 0.589 | 0.598 | 0.570 | 0.579 | 0.609 | 0.711 | 0.620 | 0.577 | 0.624 | 0.567 | 0.568 | 0.660 | 0.599 | 0.613 | 0.572 | 0.571 | 0.588 | 0.750 | 0.682 | 0.616 | 0.686 | 0.602 | 0.560 | |
Table 5: Simulated power for two treatments using the sample size NT.
| β2 | 2 | 2.5 | |||||||||||||||||||||||
| λ2 | 1.0 | 1.1 | 1.0 | 1.1 | |||||||||||||||||||||
| β1 | 1.5 | 2 | 1.5 | 2 | 1.5 | 2 | 1.5 | 2 | |||||||||||||||||
| L | λ1 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 | 1.4 | 1.5 | 1.6 |
| L*-0.1 | c=.4 | 0.931 | 0.873 | 0.814 | 0.851 | 0.774 | 0.700 | 0.962 | 0.941 | 0.886 | 0.942 | 0.876 | 0.810 | 0.944 | 0.891 | 0.838 | 0.883 | 0.806 | 0.739 | 0.968 | 0.956 | 0.914 | 0.955 | 0.902 | 0.822 |
| .5 | 0.897 | 0.807 | 0.775 | 0.821 | 0.761 | 0.711 | 0.963 | 0.906 | 0.837 | 0.911 | 0.831 | 0.776 | 0.909 | 0.840 | 0.787 | 0.840 | 0.779 | 0.727 | 0.968 | 0.940 | 0.865 | 0.938 | 0.869 | 0.800 | |
| .6 | 0.824 | 0.761 | 0.730 | 0.768 | 0.726 | 0.689 | 0.946 | 0.848 | 0.772 | 0.866 | 0.779 | 0.738 | 0.853 | 0.771 | 0.740 | 0.792 | 0.749 | 0.710 | 0.971 | 0.900 | 0.811 | 0.902 | 0.808 | 0.749 | |
| .7 | 0.755 | 0.703 | 0.687 | 0.692 | 0.651 | 0.657 | 0.888 | 0.765 | 0.726 | 0.794 | 0.700 | 0.674 | 0.772 | 0.734 | 0.727 | 0.735 | 0.701 | 0.674 | 0.948 | 0.817 | 0.735 | 0.825 | 0.744 | 0.704 | |
| L*-0.05 | c=.4 | 0.910 | 0.854 | 0.810 | 0.830 | 0.774 | 0.693 | 0.947 | 0.921 | 0.875 | 0.910 | 0.859 | 0.810 | 0.919 | 0.877 | 0.837 | 0.861 | 0.782 | 0.720 | 0.960 | 0.938 | 0.896 | 0.928 | 0.884 | 0.832 |
| .5 | 0.865 | 0.810 | 0.780 | 0.808 | 0.762 | 0.704 | 0.939 | 0.880 | 0.831 | 0.884 | 0.833 | 0.775 | 0.883 | 0.820 | 0.783 | 0.823 | 0.773 | 0.723 | 0.957 | 0.909 | 0.848 | 0.904 | 0.843 | 0.789 | |
| .6 | 0.801 | 0.754 | 0.726 | 0.752 | 0.708 | 0.679 | 0.899 | 0.828 | 0.774 | 0.839 | 0.783 | 0.736 | 0.818 | 0.766 | 0.747 | 0.778 | 0.728 | 0.700 | 0.944 | 0.857 | 0.792 | 0.863 | 0.797 | 0.753 | |
| .7 | 0.741 | 0.703 | 0.685 | 0.686 | 0.637 | 0.670 | 0.830 | 0.754 | 0.725 | 0.756 | 0.679 | 0.657 | 0.746 | 0.738 | 0.726 | 0.714 | 0.683 | 0.659 | 0.887 | 0.779 | 0.746 | 0.790 | 0.732 | 0.687 | |
| L* | c=.4 | 0.900 | 0.866 | 0.832 | 0.861 | 0.809 | 0.763 | 0.924 | 0.912 | 0.884 | 0.906 | 0.873 | 0.832 | 0.912 | 0.882 | 0.851 | 0.869 | 0.825 | 0.757 | 0.937 | 0.920 | 0.893 | 0.917 | 0.886 | 0.841 |
| .5 | 0.864 | 0.825 | 0.791 | 0.831 | 0.780 | 0.728 | 0.919 | 0.886 | 0.846 | 0.887 | 0.851 | 0.807 | 0.892 | 0.849 | 0.800 | 0.843 | 0.795 | 0.730 | 0.933 | 0.898 | 0.868 | 0.903 | 0.866 | 0.819 | |
| .6 | 0.822 | 0.772 | 0.728 | 0.777 | 0.714 | 0.667 | 0.890 | 0.842 | 0.796 | 0.847 | 0.791 | 0.741 | 0.848 | 0.794 | 0.747 | 0.796 | 0.733 | 0.675 | 0.914 | 0.863 | 0.813 | 0.875 | 0.819 | 0.761 | |
| .7 | 0.737 | 0.713 | 0.702 | 0.685 | 0.671 | 0.723 | 0.845 | 0.761 | 0.719 | 0.760 | 0.714 | 0.675 | 0.786 | 0.734 | 0.711 | 0.718 | 0.683 | 0.711 | 0.869 | 0.789 | 0.751 | 0.814 | 0.741 | 0.693 | |
| L*+0.05 | c=.4 | 0.905 | 0.889 | 0.863 | 0.890 | 0.857 | 0.818 | 0.919 | 0.906 | 0.889 | 0.909 | 0.891 | 0.866 | 0.907 | 0.898 | 0.867 | 0.895 | 0.866 | 0.817 | 0.922 | 0.910 | 0.901 | 0.917 | 0.895 | 0.886 |
| .5 | 0.879 | 0.858 | 0.812 | 0.863 | 0.821 | 0.742 | 0.912 | 0.891 | 0.869 | 0.897 | 0.871 | 0.844 | 0.896 | 0.878 | 0.829 | 0.883 | 0.835 | 0.745 | 0.914 | 0.904 | 0.882 | 0.908 | 0.886 | 0.850 | |
| .6 | 0.848 | 0.802 | 0.757 | 0.799 | 0.748 | 0.714 | 0.899 | 0.868 | 0.813 | 0.867 | 0.816 | 0.770 | 0.869 | 0.821 | 0.766 | 0.828 | 0.749 | 0.692 | 0.908 | 0.882 | 0.846 | 0.893 | 0.858 | 0.787 | |
| .7 | 0.781 | 0.753 | 0.765 | 0.745 | 0.741 | 0.782 | 0.871 | 0.808 | 0.758 | 0.803 | 0.754 | 0.724 | 0.833 | 0.775 | 0.755 | 0.775 | 0.730 | 0.750 | 0.895 | 0.839 | 0.786 | 0.841 | 0.787 | 0.736 | |
| L*+0.1 | c=.4 | 0.907 | 0.897 | 0.880 | 0.901 | 0.882 | 0.840 | 0.921 | 0.912 | 0.901 | 0.915 | 0.902 | 0.892 | 0.912 | 0.907 | 0.873 | 0.907 | 0.884 | 0.830 | 0.923 | 0.916 | 0.909 | 0.916 | 0.910 | 0.892 |
| .5 | 0.901 | 0.868 | 0.827 | 0.883 | 0.827 | 0.755 | 0.917 | 0.906 | 0.888 | 0.905 | 0.889 | 0.854 | 0.911 | 0.890 | 0.846 | 0.893 | 0.848 | 0.742 | 0.923 | 0.913 | 0.894 | 0.914 | 0.900 | 0.874 | |
| .6 | 0.860 | 0.821 | 0.785 | 0.828 | 0.781 | 0.734 | 0.912 | 0.880 | 0.845 | 0.884 | 0.849 | 0.798 | 0.888 | 0.848 | 0.793 | 0.848 | 0.790 | 0.697 | 0.916 | 0.894 | 0.858 | 0.900 | 0.865 | 0.813 | |
| .7 | 0.818 | 0.803 | 0.801 | 0.792 | 0.804 | 0.814 | 0.881 | 0.842 | 0.800 | 0.841 | 0.792 | 0.794 | 0.856 | 0.817 | 0.802 | 0.815 | 0.795 | 0.800 | 0.905 | 0.862 | 0.822 | 0.875 | 0.826 | 0.788 | |
Table 6: Powers for two treatments with 150% of sample size given in Table 4.2.
In this study, statistical analysis of count data collected from a two- stage adaptive seamless design with different durations but with the same study objectives in the two stages is discussed under a Weibull model. In particular, the comparison of the treatments is based on the medians of the distributions. Results corresponding to various types of comparison between two treatments using the combined data observed from the two stages are derived. Furthermore, the required sample sizes for the corresponding tests to achieve a given power level are determined. Since the results are developed based on asymptotic approximation, the simulation study conducted in our study shows that the type I error is well-controlled but the simulated power is less than the nominal level for tests with these sample sizes. However, simulation studies show that the nominal power level can be achieved if the sample sizes are increased by 50%. Thus, results developed in this study provide valuable insights for practitioners to determine the sample sizes in a two-stage design.