Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2018) Volume 7, Issue 3
Light aircrafts are designed to be used in both developed and undeveloped areas of a country. Hard landing conditions such as shocks and rebounds may occur. In this context, a good, efficient, robust and easy to maintain landing gear is vital. Its main role is to dissipate the energy of the impact. The aim of this work is to study an innovative light aircraft landing gear equipped with a damper. The study includes comparing its dissipation performance with two traditional light aircraft landing gears: a classical flat spring landing gear and a landing gear with Sandow cords. These systems’ modeling is carried out through three steps. Firstly, Bush tire is modeled with finite elements considering tire geometry and material specificities. Secondly, combined finite elements with structural elements are used to model the different landing gear systems. Thus, stress, deformation and energy within landing gears components could be obtained. Finally, aircraft rolling simulations are conducted. Systems’ transient responses while rolling over ramp are evaluated, as well as the efforts and rebound displacements transmitted to the aircraft. A dissipation efficiency comparative study between the landing gears is conducted. In addition, the influence of simulation’ conditions such as inflation pressure, rolling velocity or runway flatness is investigated.
Keywords: Landing gear; Numerical simulation; Tire
In this project, we will focus on light aircrafts used in undeveloped areas of a country where ground transportation infrastructure is inadequate or does not exist. Hard landing conditions such as shocks and rebounds may occur, leading to energy dis-septation issues in the landing gear. In fact, the landing gear is the component that absorbs the energy of the landing impact and carries the aircraft weight for all ground operations, including taking off, taxiing, and towing.
Although, a part of shock energies is absorbed by under-inflated tires. A conventional landing gear has a tired wheel unit, a shock absorbing unit and a supporting structure. More specifically, this study concerns light aircrafts such as light sport aircraft (LSA), ultra-light air-craft, the original Piper Cub [1-3].
These types of aircrafts can be equipped with different types of landing gears [4]. And recently, a new design has been introduced into these light aircraft landing gears (Figure 1a). It consists on using shock struts, often called oleo or air/oil struts, that use a combination of nitrogen (or compressed air) and hydraulic fluid to absorb and dissipate shock loads on landing [2].
There is no previous study nor on the advantages and inconvenient of this landing gear, neither on its dissipation efficiency in critical situations. Usually,” artisanal” landing gears’ solutions are used, such as:
• Landing gear with flat steel spring (Figure 1b) They are designed in materials such as steel, aluminium or composites that absorb the impact during landing [2-5]. Steel spring strut is one of the most common landing strut system be-because it is mechanically simple, typically lightweight, and requires very little maintenance. At touchdown, the impact energy is partly dissipated by the bending legs of the landing gear. This type has been particularly studied in the literature [6-14].
• Landing gear with Sandow cords (Figure 1c) Sandow cords are often found on tailwheel and backcountry air-planes. They are a series of elastic cords wrapped between the airframe and the flexible gear system, allowing the gear to transfer impact load to the aircraft at rates that do not damage the plane. The Sandow solution is easy to use and inexpensive but wears very quickly.
In order to evaluate the behavior of the new landing gear equipped with a damper, a comparison study is performed with the previously presented landing gear types. Numerical models need to be simple but considering all the key characteristics and must reflect the overall behavior of the aircraft. The lateral deflection of tires and the rebounds generated from rolling over the irregular runways need to be obtained. In the following, the step by step development of the models is presented and finally illustrated with simulation results. This comparison method can be applied on other aircraft landing gears versions also.
Modeling approach
Traditionally, landing gear numerical simulations have been carried out with Multi-body Dynamics (MBD) software [8,14,15-23]. Some modeling approaches are presented in this paragraph. Ambalaparambil [8] worked on the development of a Multi-degree of Freedom (MOF) model for simulation and control of the landing performances of the SAE (Society of Automotive Engineers) Heavy Lift Airplane model. As the problem is highly nonlinear and complex, initially a simplified 1-D model of this aircraft is derived and analyzed using Lagrange’s equations and energy methods. A more complex 3-D model is derived considering the dynamics of the wheels of the landing gear. Analysis with and without runway profile are performed to study the effects of the input signals on the derived model. Lopez [18] worked on a helicopter with oleo-pneumatic landing gear associated with wheels. The aim of his work was to minimize the oscillations of the tail boom and more particularly the acceleration peak during landing. First, an analytical model was developed integrating the nonlinearities induced by the tire, the damper gas chambers and the shock absorber. Lopez [18] developed in a second step a multi-body model. Detailed parametric models of each subsystem composing the whole system were developed. The assembly is carried out respecting the kinematics of the real system and a digital model of the real system visually like the demonstrator is obtained. The model is developed under Adams/ Aircraft’s commercial-business software (dynamics of multi-bodyrigid and flexible systems). Given the robustness of the computational methods, the multi-body model of the demonstrator was taken as a reference for verifying the coherence of the analytical models developed [18]. Said [22] worked on a light aircraft: the regional jet Learjet 45. The scope of his project was to develop a numerical simulator of an aircraft landing, taking into account the dynamic of the landing gear and the internal design of the shock strut. A mathematical model was first developed with VBA (Visual Basics for Applications) followed by a CAD modeling under Adams/ Aircraft. The results obtained by the CAD simulations are also considered as reference results. In this project, tires were considered and characterized with two different models (finite elements and analytical models) using two numerical codes (Abaqus and Adams). It was deduced that the pneumatic structure could con-tribute significantly to the absorption of the kinetic energy of the aircraft after its impact with the ground. The overall landing gear model is improved by integrating an Abaqus finite element model of the tire. In our study, developing a finite elements model for tires is primary in order to recreate best the rebounds transmitted to the aircraft body. Hence, multi-body approach respecting the kinematics of the real system is used combined with finite elements model for tires.
Tire modeling
Bush tires (Figure 2) play an important role in reducing the effect of road irregularities by attenuating the forces transmitted to the plane suspensions. Usually, these tires are large and low-pressured. Hence they would not sink or burst while landing on rocks. At our knowledge, there is no previous study on this type of tires. Most studies about tires have been performed in automobile field [7,13,20]. In the field of aeronautics, few studies focused on tire modeling [10,16]. Kongo et al. [16] presented a possible approach for the setting on of a numerical model based on the Finite Element Method for jumbo-jet tire. Experimental tests were performed in order to describe the inner structure of the tire. The model obtained considers the real geometry of the tire, the complex material structure and its properties as well as the interactions between the tire and the ground (contact, friction and thermo-mechanical coupling due to friction). We recall hereafter the main steps used for modeling the Bush tire.
Materials used
The rubber material is assumed to be hyper-elastic. Several models are proposed in the literature to describe the non-linear stress-strain relationship of rubber, among these we note: Arruda-Boyce [12], Ogden et al. [19] and polynomial models (Neo-Hookean, Yeoh, Mooney-Rivlin,..) [21]. In this study, experimental tests are performed on tire rubber and Figure 3 shows the normalized stress–strain curve obtained.
Tire geometry
In this work, the tire studied is a radial 26” tire, without grooves, used under-inflated for certain types of ground and has a specific structure, different from conventional tires. The tire cross-section was obtained using water-jet cutting. This method gives a highly accurate cutting plane and a very detailed image of all inner layers. The thickness of the tire cross-section is 0.006 m in the tread zone, lower than classic tires. Samples of the rein-forced rubber from different parts (tread, side-walls, ...) were cut out in order to characterize the plies: orientation, spacing between cords, cords diameter. The 2-D contour has been obtained by image processing (Figure 4). Figure 4 shows the plies (surface elements) embedded in the cross-section mesh. The final 3D geometry takes into account all plies positions and specific geometries.
As shown in Figure 3, the hyper-elastic model of Mooney-Rivlin predictions [21] matched the experimental test data. In this model, the strain energy density function is a linear combi-nation of the two first invariants of the left Cauchy-Green deformation tensor:
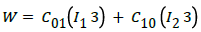 (1)
(1)
The reinforcement cords are described using an elastic model. By means of experimental tests, their Young modulus is identified as Ecords = 5:104 MPa.
3-D model
Abaqus code is used to model the final cross-section with clear contours and inner layers. Kongo et al. [16] has shown the importance of modelling the reinforcement cords and proved that the rebar model in Abaqus [5] is the most accurate mean for modelling cords. Thus, an embedded 2-D axisymmetric mesh model is obtained (Figure 4).
A combination of solid axisymmetric elements is used to mesh the homogeneous rubber and surface axisymmetric elements are used to mesh the plies. A 3-D model is then developed by revolving the 2-D mesh (Figure 5).
In order to validate the model efficiency, experimental static tests are performed. The vertical deflection of the tire is measured during loading for 3 different inflation pressures: 0.4, 0.8 and 1 bar.
Figure 6a shows the load–deflection curves obtained in comparison with the experimental results. Tire stiffness in-creases with the inflation pressure. Static simulations prove that the tire sidewalls are very flexible and deform more than other usual tires’ sidewalls.
On the other hand, the footprint shape and area obtained after loading, are also compared with the experimental results. Figure 6b shows the contact area of the tire loaded at 2.5 KN, inflated at 0.4, 0.8 and 1 bar.
The larger the inflation pressure, the smaller the contact patch. It can be noticed from these comparisons that there is a good agreement between the reference data and the values obtained with the model. Although minor differences are noticed in the contact area comparisons for high inflation pressure, due to material simplifying assumptions.
Landing gears modelling
The dimensions of landing gear’s components differ according to the aircraft type and size. The landing gears’ models developed here are mimic of actual existing models. These specific landing gears are chosen because they can be used on air-crafts of the same weight, equipped with similar tires, and for which it is easier to find experimental results. Real dimensions of struts are taken into account although some simplifying assumptions of geometry are considered.
Choosing structural components models
Multiple structural elements are used to model the whole landing gear combined with tires FE models
• Struts: All the landing gear struts are made of steel and modelled as beam elements.
• Assembly: The connectivity between the different struts is modelled by « connector » elements. These structural elements are used to define degrees of freedom that can have relative motion between two nodes, described into a coordinate system.
• Shock absorber: In this study, shock absorbers are modelled through their global response using axial connector elements. A local coordinate system with the local x-axis along the line connecting the two nodes is used. The axial connector elements could be given elastic and damping properties. Limits on relative displacement for the connector elements are also prescribed in order to meet the realistic maximum stroke of the shock absorber.
• The Sandow cords are modelled with elastic behaviour described by an S-shaped stress-strain non-linear function. The real values of forces are not mentioned in order to ensure confidentiality.
• The oleo-pneumatic shock absorber (damper) combines gas spring with oil damping. Thus, its modelling requires considering both spring forces and damping forces. Spring forces are modelled as presented in Figure 7a. The initial part is linear and presents the initial shift for obtaining the pre-load. The second part is obtained by a law of poly-tropic expansion [9,17]:
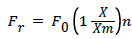 (2)
(2)
with spring force Fr, pre-stress force F0, oleo stroke x, oleo gas length xm, polytropic coefficient n. Eventually, the spring forces setting of the Sandow cords and the damper are different. The maximum strokes and the initial preload are different. On the other hand, the damping properties of the damper are generally described by the laws of viscous fluid:
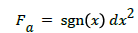 (3)
(3)
With damping force Fa, damping coefficient d that differs if x < 0 or x > 0, the velocity x. The damping behavior is modeled as presented in Figure 7b. The real values of forces are not mentioned in order to ensure confidentiality.
• Leaf spring: Modeled using classical homogeneous shell elements.
Model settings
The static analysis was carried out in the following manner:
• The tires are subjected to a constant inflation pressure according to specifications (between 0.4 bar and 1.2 bar).
• A frictional contact problem in the FEM tire model is de-scribed between a deformable body (tire) and the rigid body (ground). The contact is described using Signorini laws. The friction is described using Coulomb laws and a constant friction coefficient is used.
• A vertical load of 5 KN is applied on the frame, presenting the weight of the aircraft. A static position is obtained for each landing gear.
Static simulations
The three landing gears modeled are presented in Figures 8, 9 and 10 and will be referred hereafter as LGM (the Metallic spring steel), LGS (with Sandow cords) and LGD (equipped with a Damper). Static simulations are performed. The three landing gears are loaded at 5 KN. Figures 8a, 9a and 10a indicate the static loaded position for tires inflated at 0.8 bar.
Model validation
Given the complexity of the new landing gear equipped with a damper and the fact that there is no related data in the literature, it was judged necessary to perform experimental tests and validate the numerical model developed here.
The drop-test is a dynamic test used in aeronautics in order to investigate a structure in vertical impact. This test must comply with several regulations and is used primarily to certify the aircrafts. In this work, drop tests were performed on the landing gear equipped with a damper. And the peak acceleration, which is an important indicator when evaluating the shock fragility of landing gears [14,15], is measured.
As we can see in Figure 11, the landing gear is fixed on an articulated frame which can be loaded according to the characteristics of the aircraft. The load is 5 KN and the inflation pressure is 2 bar. HDPE plates are placed under the tires in order to facilitate lateral sliding of the tires. The frame is released from a predefined height according to the desired drop velocity. The maximum deceleration during a drop-test is measured with an accelerometer.
A comparison between experimental and numerical results obtained for the landing gear equipped with a damper are presented in the Table 1. The error does not exceed 6%. Thus, our numerical model is able to predict the overall dynamic behaviour of the landing gear equipped with a damper.
| Drop height (m) | Experimental G-factor | Numerical G-factor |
|---|---|---|
| 0.24 | 2.1 | 2.14 |
| 0.787 | 3.1 | 3.25 |
Table 1: Drop test results.
Dynamic rolling simulations
Starting from the static position obtained after loading, the numerical dynamic simulations of the landing gears in rolling situations were performed within two steps:
• An acceleration phase, applied on the frame.
• A steady phase of rolling at constant velocity of 50 Kph is applied on the frame during rolling over a ramp (Figure 12).
The runway is described using a rigid body definition, is flat with one ramp of 1 m length and 0.2 m height. This rolling scenario is inspired from real test sessions undergone by light aircrafts. The ramp is positioned ahead of the landing gear to make sure the rolling landing gear can reach a steady state condition before it reaches the ramp.
Steady state configurations are shown in Figures 8b, 9b and 10b. The time t=5 s matches the time when the landing gear reaches the ramp and the time t=5.1 s matches the time when the landing gear leaves the ramp. The amplitudes and frequencies of rebounds undergone by the frame are studied as well as tire displacements.
The landing gears dissipation efficiency is evaluated based on rebounds amplitudes and frequencies after the touchdown (after the resumption of contact). Figure 13 shows the most important parameters studied while analyzing the overall landing gears responses.
Influence of the inflation pressure
Three cases of inflation pressure P0 of 0.4, 0.8 and 1 bar respectively are presented. The vertical response of LGD rolling on a runway with a ramp is shown in Figure 14. Figure 14a shows the frame vertical displacement while Figure 14b shows the tire vertical displacement.
The rebounds generated after passing the ramp are analyzed. The zero position indicates the steady state for the rolling landing gear. Rebounds amplitude decreases if inflation pressure decreases (Figure 14a).
Moreover, if inflation pressure increases, crushing amplitude increases. This may be explained by the fact that tires deform as much as they are under-inflated. Tires’ deflection affects the frame displacement significantly.
Influence of the rolling velocity
The influence of rolling velocity variation on the landing gear vertical response is investigated. Two cases of rolling velocities are presented: V=25 Kph and V=50 Kph. The vertical response of LGD rolling on a runway with a ramp is shown in Figure 15. Dissipation efficiency after going beyond the ramp is not affected by the velocity variation (t >6 s) (Figure 15a). For 5s
Influence of runway flatness
In order to depict the influence of the runway flatness, rolling simulations over small cleats (0.02 m height) are performed. The vertical displacement of the frame and tires of LGD are compared with results from rolling over flat runway in Figure 16.
A comparison between the three landing gears
Rolling over ramp: Rolling simulations are performed for the three landing gears, under the same simulation conditions such as inflation pressure (0.8 bar) and rolling velocity (50 KpH) and vertical load (5 KN). The vertical responses of LGM, LGS and LGD rolling on a runway with a ramp are presented in Figure 17.
Figure 17a describes the frame vertical displacement while Figure 17b shows the tire vertical displacement. After going beyond the ramp, 3 rebounds are obtained for LGM, 2 rebounds are obtained for LGD and 1 rebound is obtained for LGS (Figure 17a). Re-bound amplitude is decreasing in all three cases due to energy dissipation [9,13,15,17,20,23].
LGD presents the lowest rebound amplitude aіer the touchdown. Concerning tire displacements aіer leaving the ground, only LGD does not present vertical perturbations generated by lateral displacements. Further less, Figure 18 shows tires spacing during rolling, relative to the initial spacing. It is clear that in the case of LGD, tires are more stable compared to the other cases. Rolling over onesided ramp: Rolling simulations over one-sided ramp are performed for the three landing gears, under the same simulation conditions such as inflation pressure and rolling velocity (Figure 19).
As above, the vertical displacement of the aircraft and the centers of the tires are analyzed respectively in Figure 20a. It is necessary to analyze the behavior of both tires since there is no more symmetry of the results (Figures 20b and 20c). Tire 1 is on the ramp side, while tire 2 encounters no obstacle.
As in the case of rolling over a ramp, rebound amplitude of aircraft displacement is decreasing in all three cases due to energy dissipation. LGD presents the lowest rebound amplitude after the touchdown. Its overall dissipation seems to be the most efficient in this case.
On the other hand, tires’ oscillations in the three cases are analyzed. The contact area gives information about whether the tire is in contact with the ground or not (Figures 21, 22 and 23). Figure 20 shows that in the case of LGD, tire 2 undergoes oscillations of higher amplitude compared to the other landing gears. In addition, referring to Figure 23, tire 2 of LGD loses contact as frequently as tire 1.
LGD shows a significant rolling phenomenon in the heading direction. Moreover, in the case of LGS, Figure 22 shows that the tire 2 does not lose contact which can indicate that the aircraft is more balanced. In this case, one can assume that there is no coupling between tires since the rebounds under-gone by tire 1 do not generate rebounds in tire 2. Nevertheless, the amplitudes and frequencies of generated rebounds in LGS (Figure 20a) are the highest.
In the case of LGM, the landing gear is also rolling in the heading direction (Figure 23), but the amplitudes are less important, and the tires’ displacements present a sinusoidal envelope corresponding to the elastic deformations undergone by the steel struts. In fact, energy in LGM is only dissipated through the tire’s deformation and lateral friction.
In conclusion, the overall dissipation response of the landing gear does not reflect necessarily the balance of the landing gear and phenomena such as rolling, or pitching should be taken into account.
The present study evaluates the behavior of a new landing gear equipped with a damper. Its response is compared to two classical solutions, a leaf landing gear and a sandow one. Each landing gear is modeled independently. All models use the same tire model, validated by experimental data on vertical deflection and contact area criteria. Realistic geometry and materials properties for struts, in addition of real shock absorber laws are considered. This modeling approach showed its validity in the literature and its efficiency through the numerical results obtained here. Also, the numerical model of the new landing gear is validated by drop test experimental data. The precision is sufficient for studying the problematic proposed in this paper. On the other hand, landing or rolling on irregular terrains is the main problem of these light aircrafts, for which the example of rolling over ramp is considered an illustrative test. This test case is studied. Landing gears dissipation efficiency is evaluated through the amplitudes and frequencies of the rebounds transmitted to the frame body after touchdown. The landing gear equipped with a damper seems to be the most efficient in the specific case of rolling over a ramp. Even in the case of rolling over one-sided ramp, its amplitudes are the lowest. Furthermore, the influence of simulation parameters such as velocity and inflating pressure on landing gears behavior on rolling over ramp are highlighted. Dissipation efficiency after going beyond the ramp is not affected by the velocity variation. More-over, the tires’ inflation pressure has a considerable effect on the rebounds’ amplitude although it does not affect the comparative conclusion.