Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2015) Volume 4, Issue 3
The objective of this study was to develop an efficient and accurate computational methodology to predict detailed thermo-fluid environments of a single flow element in a hypothetical solid-core nuclear thermal thrust chamber assembly. Several numerical and multi-physics thermo-fluid models, such as chemical reactions, turbulence, conjugate heat transfer, porosity, and power generation, were incorporated into an unstructured-grid, pressure-based computational fluid dynamics solver used in this investigation. A secondary objective was to develop a porosity model for simulation of the whole solid-core nuclear thermal engine without resolving thousands of flow channels inside the solid core. Detailed numerical simulations of a single flow element with different power generation profiles were conducted to investigate the root cause of a phenomenon called mid-section corrosion that severely damaged the flow element assembly of early solid-core reactors. Under the assumptions employed in this effort and for the first time, the result demonstrated flow choking in the flow element. The possibility of flow choking in part of the flow element indicated a potential coolant mass flow imbalance, which could lead to a high local thermal gradient in coolant-starved flow elements and possibly the eventual mid-section corrosion.
<Keywords: CFD; Nuclear thermal propulsion; Conjugate heat transfer; Porosity model
C1, C2, C3=turbulence modeling constants (1.15, 1.9, and 0.25)
CD=drag coefficient
Cf=friction factor
Cp=heat capacity
D=drag force
Dp=channel diameter of a flow element
d= pipe diameter
fD, fn,=modeling constants
h, ht=static and total enthalpies
I=time index during navigation
j=waypoint index
Lp=flow element length
q=surface heat flux
qp=heat source from power generation per volume
Re=Reynolds number
T=temperature
t=time
Vi, Vj, VI=tensor notation for velocity component in Cartesian coordinates
Wp=width of a flow element
Xi, Xj, XI=tensor notation for Cartesian coordinates
x=axial distance
δij=Kronecker delta
φ=magnitude of power generation
μ=fluid viscosity
μt=eddy viscosity
σk, σε=turbulence modeling constant (0.75, 1.15)
τij=stress tensor
Subscripts
b=boundary
c=cell center
d=diameter
g=gas/fluid
s=solid
t=turbulent flow
w=wall
The nuclear thermal rocket is one of the candidate propulsion systems for future space exploration, including traveling to Mars and other planets of the solar system. Nuclear thermal propulsion can provide a much higher specific impulse than the best chemical propulsion available today. A basic nuclear propulsion system consists of one or several nuclear reactors that heat the propellant/coolant (e.g. hydrogen) to high temperatures and then allow the heated working fluid and its reacting product to flow through a nozzle to produce thrust. In the 1970s, a solid-core design [1,2] for the nuclear reactor was developed and tested under the Rover/NERVA programs. Those studies showed that the solid-core reactor is a feasible concept producing specific impulses exceeding 850 sec. The solid-core reactor operates like a heat exchanger. It consists of hundreds of heat generating solid flow elements, with each flow element containing tens of flow channels through which the hydrogen propellant absorbs heat before entering a nozzle to generate thrust. Figure 1 shows a cross-sectional view of the layout of the flow element assembly and a 19-channel flow element.
To achieve maximum efficiency, the reactor often operates at a very high temperature and power density. However, the results of Rover/ NERVA tests indicated that under those conditions the flow element may fail due to a phenomenon called mid-section corrosion [3,4], which imposes real challenges to the integrity of the flow element. Mid-section corrosion refers to a crack in the coating layer between the solid fuel and hydrogen flow, which is designed to protect the solid fuel from chemical attack by the hot hydrogen. Mid-section corrosion can lead to an excessive mass loss of the flow element material in that region. The prevailing cause of mid-section corrosion is suspected to be unmatched thermal expansion coefficients between the flow element and its coating material [3]. Hence, most of the studies conducted to prevent the issue of mid-section corrosion were to match the thermal expansion coefficients of the flow element and its coating materials. We believe, however, the cracking of the coating material is the symptom and not the cause. According to the Rayleigh line theory, flow with continuous heat addition in a long channel could chock. That could cause hydrogen mass flow maldistribution among the flow channels, resulting in an uneven head load distribution in the solid-core, eventually cracking the coating material. Choking in the heated long flow channel is, therefore, the real cause of the mid-section corrosion. Demonstrating choking which occurs in the flow channel, however, is not trivial since it is extremely difficult and expensive to measure the detailed thermal-fluid environment within the entire flow element.
Therefore, the objective of this effort was to develop an efficient and accurate multiphysics thermal-fluid computational methodology to predict environments in a single flow element, similar in operating conditions and design parameters to those in a hypothetical Small Engine [1]. The computational methodology was based on an existing unstructured-grid Navier-Stokes internal-external computational fluid dynamics (CFD) code (UNIC [5-7]). The UNIC code has been well validated and employed to simulate a wide variety of engineering problems. Conjugate heat transfer (CHT) formulations for coupling fluid dynamics and conductive heat transfer in solids were developed and tested in the present study. Power profiles representative of those occurring in typical solid-core reactors were used in lieu of the neutronics modeling. In addition, in order to support a separate global analysis of the entire thrust chamber [8,9], a porosity model capable of describing the flow characteristics and heat transfer inside the entire solid-core was developed. The results of the detailed conjugate heat transfer modeling of a powered single flow element and the development of the porosity model are reported herein.
Computational fluid dynamics
The employed CFD solver, UNIC, solves a set of Reynolds-averaged governing equations (continuity, Navier-Stokes, energy, species mass fraction, etc.) that satisfies the conservation laws. The set of governing equations can be written in Cartesian tensor form:
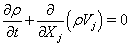 (1)
(1)
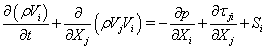 (2)
(2)
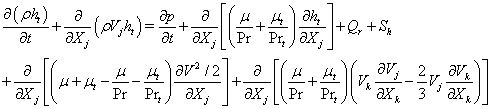 (3)
(3)
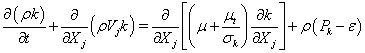 (4)
(4)
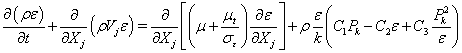 (5)
(5)
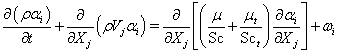 (6)
(6)
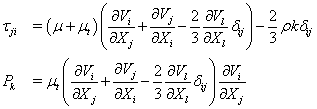 (7)
(7)
where ρ is the fluid density, p is the pressure, v is the mean total velocity, Vi, Vj and VI are the mean velocity components of the Cartesian coordinates, ht and h are the total and static enthalpies, k is the turbulence kinetic energy, Pk and ε are the production and dissipation rates of turbulence, αi and ωi are the mass fraction and production rate of i-th species, Q is the radiative heat flux, Si and Sh are the source and sink terms of the momentum in the i -th coordinate and energy equations, τji represents the sum of the viscous and Reynolds stress tensors, Pr and Prt are the Prandtl and turbulent Prandtl numbers, and Sc and Sct are the Schmidt and turbulent Schmidt numbers. Detailed expressions for the k-ε models and wall functions can be found in Ref. [10]. An extended k-ε turbulence model [11] was used to describe the turbulent flow. A modified wall function approach [12] was employed to provide wall boundary layer solutions that are less sensitive to the near-wall grid spacing.
A predictor and multi-corrector pressure-based solution algorithm [13,14] was employed in the UNIC code to couple the set of governing equations such that both compressible and incompressible flows could be solved in a unified framework without using ad-hoc artificial compressibility or a pre-conditioning method. The employed predictorcorrector solution method [5] is based on the modified pressurevelocity coupling approach of the SIMPLE-type [14] algorithm which includes the compressibility effects and is applicable to flows at all speeds. In order to handle problems with complex geometries, the UNIC code employs a cell-centered unstructured finite volume method [6,7] to solve for the governing equations in the curvilinear coordinates, in which the primary variables are the Cartesian velocity components, pressure, total enthalpy, turbulence kinetic energy, turbulence dissipation, and mass fractions of chemical species.
A second-order central-difference scheme is employed to discretize the diffusion fluxes and source terms. For the convection terms, a second-order multi-dimensional linear reconstruction approach, suggested by Barth and Jespersen [15], is used in the cell reconstruction to evaluate fluxes at the cell face based on the cell-centered solution. To enhance the temporal accuracy, a second-order dual-time subiteration method is used for time-marching computations. A pressure damping term by Rhie and Chow [16] is applied to the mass flux at the cell interface to avoid the even-odd decoupling of velocity and pressure fields. All of the discretized governing equations are solved using the preconditioned Bi-CGSTAB [17] matrix solver, except the pressurecorrection equation which has an option to be solved using GMRES [18] matrix solver when the matrix is ill-conditioned. An algebraic multi-grid (AMG) solver [19] is included such that users can activate it to improve the convergence if desired. In order to efficiently simulate problems involving large number of meshes, the UNIC code employs parallel computing with domain decomposition, where exchange of data between processors is done by using Message Passing Interface (MPI) [20]. Domain decomposition (partitioning the computational domain into several sub-domains handled by different computer processors) can be accomplished by using METIS [21] or a native partitioning routine in the UNIC code.
Conjugate heat transfer
The framework of conjugate heat transfer (CHT) is to solve the heat transfer in the fluid flow and the heat conduction in the solid in a coupled manner. The governing equation describing the heat transfer in the fluid flow is shown in Eq. (3), where the heat conduction in the solid can be written as:
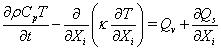 (8)
(8)
where Qv and Qp represent source terms from volumetric and boundary contributions, respectively. k and Cp denote the thermal conductivity and capacity of the solid material, respectively. In the case of simulating solid core with power generation, Qv includes the energy source Qp, which depends on power generation distribution functions employed. In the present study, two power distribution functions were examined: (i) pure cosine function in the axial direction with clipped cosine function in the radial direction and (ii) clipped cosine function in the axial direction with clipped cosine function in the radial direction. The temperature value at the fluid-solid interface was obtained by enforcing the heat flux continuity condition, i.e. Qs=-qw where qw is the heat flux from the fluid to the solid calculated by solving Eq. (3) including the turbulence effect, if applicable. In order to achieve numerical stability and enforce the heat flux continuity condition, an implicit treatment of the temperature at the fluid-solid interface was employed. In this approach, Eq. (8) can be discretized as
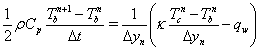 (9)
(9)
where the superscripts n + 1 and n denote the values at the next and current time levels, respectively. Tb and Tc are the temperatures at the fluid-solid interface and at the center of the solid cell next to the fluidsolid interface, in respect. 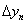 represents the normal distance from the interface to the center of the solid cell next to the fluid-solid interface. Only half of the solid cell is involved in the control volume, which accounts for the 1/2 factor on the left hand side of the above equation. It can be seen that this scheme can be applied to both transient- and steady-state simulations. For steady-state simulations, an acceleration factor can be used to improve convergence of heat conduction in the solid. Implementation of the implicit treatment has been validated [22] by comparing computed results with those of the standard heat transfer SINDA code [23].
represents the normal distance from the interface to the center of the solid cell next to the fluid-solid interface. Only half of the solid cell is involved in the control volume, which accounts for the 1/2 factor on the left hand side of the above equation. It can be seen that this scheme can be applied to both transient- and steady-state simulations. For steady-state simulations, an acceleration factor can be used to improve convergence of heat conduction in the solid. Implementation of the implicit treatment has been validated [22] by comparing computed results with those of the standard heat transfer SINDA code [23].
Porosity model
In the present study, a porosity model was developed to represent the momentum and energy transport through an assembly of flow pipes and the heat conduction through the solid material within a flow element. The porosity model computes separate temperatures and thermal conductivities for both the solid material and fluid flow. The momentum and energy equations for the fluid flow are similar to Eqs. (2) and (3), except the source terms are modified to account for the extra friction loss and heat transfer. The source term of the momentum equation in the i-th coordinate, Eq. (2), can be expressed as
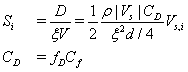 (10)
(10)
Where D is the drag force modeled by the porosity model, ξ is the porosity factor for the porous region, Vsi is the superficial flow velocity in the i-th coordinate through the porous region, d is diameter of the flow channel, V is the total volume of the porous region, CD is the drag coefficient, and fD is a modeling constant that will be tuned for the geometry of interest in the present study by comparing solutions of the porosity model and the detailed CHT model. An empirical correlation of the friction factor (Cf) for the flow through a pipe, known as the Blasius formula [24], is used and expressed as follows.
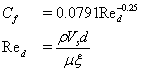 (11)
(11)
The source term for the energy equation (Eq. (3)) can be calculated as
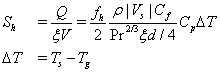 (12)
(12)
where Q is the heat sink/source due to the fluid-solid interaction in the porous region, Pr is the Prandtl number of the fluid, fh is a modeling constant that will be tuned by comparing solutions of the porosity model and the detailed CHT model, and Ts and Tg are the temperatures of the solid and fluid at the same location, respectively. In addition, the source term of the heat conduction equation (Eq. (8)) in the porous region can be calculated as
 (13)
(13)
Numerical meshes
In the present study, various flow element geometries were simulated, such as different flow channel diameters, with and without a coating layer in the solid core, and different flow channel lengths. A geometry/grid template was developed based on MiniCAD [25-27] to expedite the geometry and grid generation process by allowing the user to interactively change 1) the ratio of the gap between flow channels to the diameter of the flow channel, 2) the ratio of the size of the flow element to the diameter of the flow channel, 3) thickness of the coating layer, and 4) the length of the flow element. The procedures of using MiniCAD to generate geometries and solid meshes are detailed in Ref. [28]. The surface mesh used for creating a 3-D volume mesh was also generated with MiniCAD using a direct advancing front method [29,30]. For volume mesh generation, two approaches were used. One was a method to create regular hybrid meshes based on an advancing layers method. In this method, a multiple marching direction approach was employed to create better control volumes around sharp convex corners [31]. The other volume mesh generation method was an extrusion method based on a 2-D mesh to create volume meshes more easily. In the present study, a 60° pi-section of a single flow element, as shown in Figure 2, was simulated. Figure 3 shows the 2-D crosssectional mesh employed to generate the 3-D hybrid volume mesh inside the flow element, as shown in Figure 4, using the extrusion method. The purpose of these hybrid mesh generation efforts was to minimize numerical diffusion and the number of cells used to descritize the computational domain with a very large aspect ratio.
Full-length single flow element with power generation
A coolant (gaseous hydrogen) flowing through the full-length, innermost flow element with a hypothetical power generation profile was simulated. The purpose was to investigate the root cause of midsection corrosion in terms of fundamental flow and heat transfer principles and not noticeable symptoms such as mismatching thermal expansion coefficients between the flow element and its coating materials. The layout and geometric definitions of the single flow element simulated are similar to those illustrated in Figure 2, where only 1/6 of the flow element (shaded area in Figure 2) was considered in the numerical simulation due to geometrical symmetry. An adiabatic boundary condition was imposed at the top surface of the flow element. The geometric dimensions of the flow element and the inflow conditions were obtained from Ref. [4] and are listed in Table 1. The smallest flow channel diameter was selected among the three diameters considered in Ref. [4]. Not only because it provides the highest theoretical heat load to the working fluid, but also it is the most likely case for flow choking. In this study, a coating layer, which has different thermal properties from those of the flow element, with a thickness of 0.127 mm was also modeled for each flow channel. This was done to imitate those flow elements in the legacy engine test [3], in which the coating layer was added to protect the carbonaceous compound in the flow element from the chemical attack by the heated hydrogen. It is noted that, in the present simulation, the thermal properties of the flow element and the coating layer vary with temperatures, while the values listed in Table 2 are the properties at a temperature of 300 K only. A hybrid mesh system was used to model the flow element, as shown in Figure 4. An entrance region and an exit region were added to the upstream and downstream of the flow element, respectively. Total number of cells used was 4.5 million. The heat transfer between the fluid flow and the solid fuel was simulated with the CHT model. A one-step elementary reaction model was employed to model the hydrogen dissociation and recombination processes at high temperatures.
| Flow Element Geometry | Inflow conditions (H2) | ||||
|---|---|---|---|---|---|
| Element width (Wp) | Channel diameter (Dp) | Element length (Lp) | Pressure | Temperature | Mass flow rate |
| 19mm | 2.05 mm | 890 mm | 39.05atm | 279 K | 0.0147 kg/s/element |
Table 1: Geometry of a flow element and coolant flow inlet conditions.
| Thermal conductivity | Density | Specific heat | |
|---|---|---|---|
| Flow element | 91 W/m.K | 6142 kg/m3 | 468.4 W.s/kg.K |
| Coating layer | 19W/m.K | 6531 kg/m3 | 368 W.s/kg.K |
Table 2: Thermal properties of flow element and coating layer at 300 K.
For the power generation from the solid fuel grain, a cosine distribution in the radial direction (maximum power at the center of the innermost flow element and zero power at the edge of the outermost flow element) was specified. Two axial distribution curves of power generation (φ) were investigated. Case #1 has a pure cosine power distribution, Case #2 has a clipped-cosine power distribution, and those distributions can be expressed as
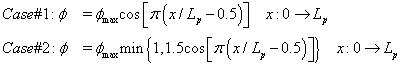
Where φmax is the maximum power and Lp is the length of the flow element. In this study, various power generation levels were simulated, and it was found that flow choking occurred in some coolant channels as the power level reached about 80% of the maximum power value. Once the flow choking occurs, further increase of heat addition will lead to the reduction of mass flow rate in the flow channel, equivalent to shifting from one Rayleigh line to another one as described in Ref. [32]. This could cause undesirable mass flow mal-distribution, resulting in uneven thermal load in the flow-element matrix, leading to the eventual cracking of the coating material. Unfortunately, further increase of the power led to unrealistic numerical solutions because of the boundary conditions employed (fixed mass at the inlet and mass conservation at the exit). This set of boundary conditions was used because only a 1/6 segment of one flow element was simulated, and thus, a nozzle that would have allowed mass flow reduction at higher power level cannot be included. Since determining whether flow choking could occur in the flow channel is our goal, hence, only the results obtained based on 80% maximum power level are presented herein.
The numerical results of power generation Cases #1 and #2 are plotted in Figures 5-10. Figure 5 shows the pressure, temperature, and Mach number contours at the symmetry boundaries and solid-fluid interfaces of the power generation Case #1, while Figure 8 shows those features of the power generation Case #2, respectively. As can be seen from the Mach number contours, the coolant is choked near the end of the flow channel for both power generation distributions. As stated earlier, the occurrence of flow choking in some of the flow channels can lead to uneven flow rate distributions among flow channels and may cause undesirable high temperatures. This clearly shows that the employed 3-D numerical model with detailed physics included can provide the critical information needed for assessing the mid- section corrosion phenomenon. It is noted that these two plots are re-scaled due to extremely large aspect (length-to-width) ratios such that the contours are viewable and distinguishable. Figure 6 shows the pressure distributions along the centerlines of the center and outer flow channels and temperature distributions along 7 axial lines of the power generation Case #1. The location of each line is depicted in Figure 3 (Line #1: centerlines of the center flow channel; Line #2: the line along the mid-point of the coating layer around the center flow channel; Line #3: the line along the mid-point between the center and outer flow channels; Line #4: the line along the inner mid-point of the coating layer around the outer flow channel; Line #5: centerlines of the outer flow channel; Line #6: the line along the outer mid-point of the coating layer around the outer flow channel; Line #7: the line between the outer flow channel and the edge of the flow element). In the temperature distribution plot, the location of the maximum temperature gradient along each line is also marked with a symbol which has the same color as each line. It can be seen that Lines #2 and #4 have the same maximum temperature gradient locations, which are very close to that of Line #3. The axial temperature distribution is qualitatively similar to that of 1-D calculation. Some researchers think that the location of the maximum temperature gradient is critically linked to the potential corrosion of the flow element caused by different thermal expansion coefficients between the coating layer and the fuel. Hence, temperature distributions in the radial direction (across the solid-fluid interface) at two maximum temperature gradient locations (of the coating layer and center flow channel) are shown in Figure 7. These two axial locations can be seen in Figure 6. The radial temperature profiles reveal that substantial thermal gradients occur at the fluid-coating interface and the coating-solid fuel interface. This may be attributed to the large difference of thermal conductivities between the coating material and the fuel, as shown in Table 2. Though 1-D calculations are efficient, they can only provide estimation of axial temperature distributions and maximum thermal gradient locations. Whereas, in addition to providing a flow environment, 3-D detailed simulations are able to predict detailed temperature gradients across different materials and fluid for thermal stress and fracture analyses of the flow elements. Hence, the numerical result presented in this paper is the first of its kind to provide a detailed thermal-fluid environment in the flow element needed for assessing the occurrence and cause of mid-section corrosion.
Figure 9 shows axial temperature distributions of power generation Case #2, which are similar to those of figure 6 except that the locations of maximum thermal gradient are further upstream than those of Case #1. This is expected because power generation Case #2 has a clipped cosine distribution, where the power rises up to its peak value faster in the axial direction. Temperature distributions in the radial direction at the same two maximum thermal gradient locations are plotted in Figure 10. Substantial thermal gradients at the fluid-coating interface and the coating-fuel interface also can be observed. However, the level of thermal gradient at the coating-fuel interface is relatively smaller than that of power generation Case #1. This can be attributed to the characteristics of the clipped cosine distribution, which has a larger area subjected to the peak power source but has a smaller peak power (such that the overall energy inputs for both cases are the same). The exit temperatures of both cases are almost identical, having a value about 2660 K. Though the predicted maximum temperature of the flow element simulated is below 3000 K for both power distributions, the results presented here were obtained based on 80% of a designed power level, and thus the maximum flow element temperature would be much higher. It is also noted that the results presented here were obtained from a steady-state study, and thus, the thermal gradient and the flow element temperature could be much larger during transient startup as pointed out by Wang et al., [10]. Furthermore, several approximations in boundary conditions and power distribution profiles were made in the present single-element simulation. For future study, 3-D numerical simulations of multiple flow elements with a downstream nozzle are necessary to include the inter-element effect and to improve the fidelity of the employed numerical model.
Porosity model development
Numerical experiments of simulating detailed coolant flow through short-length flow elements with a fixed boundary wall temperature (Tw) using the CHT model were conducted. The results were utilized to calibrate the modeling constant employed in the porosity model. The computational domain and boundary setup are shown in Figure 2. In the numerical experiments conducted, the flow element has a width of 19.1 mm, length of 110 mm, and the inlet flow conditions are the same as those shown in Table 1, except the pressure is 34 atm. Even though the flow element was shortened from 890 mm to 110 mm to save computational time, a length-diameter ratio (Lp/Dp) of 55 is long enough to obtain a fully developed flow for calibrating the porosity model. Two groups of numerical experiments were conducted. There first group consists of three cases, in which the flow channel diameter was 2.05 mm, and the wall temperatures were 3000 K, 2000 K, and 1000 K, respectively. In the second group, the wall temperature was set to be 3000K, while three flow channel diameters of 2.05 mm, 2.29 mm, and 2.54 mm were modeled. A hybrid mesh system of 1.8 millions cells was used to simulate the coolant flow through a flow element using CHT. In these numerical simulations, the thermal properties of the flow element (UC-C-ZrC composite) vary with temperature and can be found in Ref. [3], where the values of those properties at a temperature of 300 K are listed in Table 2.
The numerical results of the first group (varying wall temperatures) and second group (varying flow channel diameter) follow the similarity rule, and thus, only those in the case with a wall temperature of 3000 K and a flow channel diameter of 2.05 mm is plotted as shown in Figures 11-13. Figure 11 shows the pressure and temperature distributions at each boundary including the fluid-solid interface. The streamlines and velocity vectors of the fluid flow near the entrance and exit of the flow element are illustrated in Figure 12. Figure 13 shows the pressure distributions along the centerlines of the center and outer flow channels and temperature distributions along 4 axial lines (Line #1: centerlines of the center flow channel; Line #3: the line between the center and outer flow channels; Line #5: centerlines of the outer flow channel; Line #7: the line between the outer flow channel and the edge of the flow element). The location of these axial lines is illustrated in Figure 3. In the temperature plot of Figure 13, the temperatures in the fuel port for Lines #3 and #7 are those in the solid grain, while the rest are in the fluid flow. Meanwhile, the pressure drops as the temperature rises in the fuel port or flow element. The results with the detailed CHT model were used to calibrate the porosity model.
The aforementioned cases simulated using the CHT model were repeated with the porosity model. A hybrid mesh system of 23 k cells was used for cases with the porosity model, which is much coarser than that with the CHT model. The modeling constants of the employed porosity model, shown in Eqs. (10) and (11), were calibrated based on the case of Tw=3000 K and Dp=2.05 mm, and those were calibrated to be fD=18, and fh=0.22. That case was chosen because the 3000 K wall temperature is closest to that calculated in the simulation of the full-length flow element with power generation and CHT. Figure 14 shows the calculated temperature and pressure contours of this case. Figures 15 and 16 show comparisons of axial pressure gradients and temperatures between the CHT and porosity models. Figure 15 compares those at a fixed channel diameter (Dp=2.05 mm) and 3 different wall temperatures (Tw=1000, 2000, 3000 K), while Figure 16 compares those at a fixed wall temperature (Tw=3000 K) and 3 different channel diameters (Dp= 2.05, 2.29, 2.54 mm). At a fixed channel diameter, Figure 15 shows that temperature profiles calculated with the porosity model match very well with those of the CHT model. The predicted pressure drop of the porosity model agreed very well with that of the CHT model at a wall temperature of 3000 K, but the discrepancies are larger for the other two wall temperatures. At a fixed wall temperature of 3000 K, Figure 16 shows the predicted pressure drops of the porosity model agree reasonably well with those of the CHT model. The temperature profiles predicted by both models agree well at a channel diameter of 2.05 mm, but the discrepancies are larger for other two channel diameters. The cause for the discrepancy between the porosity and CHT models may be attributed to several factors. Since the local heat transfer and drag coefficients are highly dependent on the local flow Reynolds numbers, the value of the fluid viscosity needs to be accurately accounted for. In the present study, the fluid viscosity of air, instead of hydrogen, was used, which could be one of the causes of the discrepancy. The accuracy of the correlation between the fluid viscosity and temperature employed in the code also needs to be further examined. The Blasius formula for the friction loss coefficient, developed based on the isothermal flow, may cause some errors in the non-isothermal fluid, and thus requires further refinement. The result shows a need for further investigation of the empirical correlations of the porosity model employed. Nevertheless, it was estimated that the targeted design conditions are close to the calibrating conditions (maximum Tw=3000 K, Dp=2.05 mm); hence, the calibrated porosity modeling constants are a good starting point for computing the global performance of the targeted nuclear thermal thrust chamber of the hypothetical Small Engine [1].
In this effort, pertinent numerical models, such as conjugate heat transfer, power generation, and porosity modeling, were developed and implemented into an existing CFD code and were successfully applied in simulating the thermal-fluid environment of a single flow element in a nuclear thermal thrust chamber. The use of the porosity model showed promise as an efficient numerical approach for simulating an assembly of a huge number of flow elements, though further study may be needed to extend its applicability for general purposes. A detailed numerical analysis of a powered flow element using the CHT model provided the insight of the thermal-fluid environment. The results showed that detailed 3-D CFD simulations provided critical information that cannot be obtained from simple 1-D calculations. The numerical result indicated large thermal gradients at the fluidcoating and coating-fuel interfaces for the selected fuel and coating materials, which demonstrated the noticeable symptoms of the midsection corrosion problem. Most importantly and for the first time, the numerical results indicated that even at 80% of the maximum power level, some flow channels showed flow choking. The occurrence of flow choking in flow channels could cause non-uniform flow distributions among flow elements and produce undesirable high heat load in channels that were starved of coolant flow. No other researchers have ever raised the issue of flow choking in the flow elements, and the possibility of flow choking should be considered in the future solidcore nuclear thermal reactor design.
This study was supported by a Nuclear Systems Office task entitled “Multiphysics Thrust Chamber Modeling,” of which Wayne Bordelon was the project manager. Steve Simpson and Karl Nelson provided operating conditions for the hypothetical nuclear thermal engine. Bill Emrich suggested the cosine power profile. Thermal properties provided by Panda Binayak, Robert Hickman, and Bill Emrich are also acknowledged. Assistance by Doug Ross of the Enabling Technology Lab at UAB in developing the geometry/grid template to support this study is appreciated.