Advances in Automobile Engineering
Open Access
ISSN: 2167-7670
ISSN: 2167-7670
Research Article - (2016) Volume 5, Issue 1
Brake squeal is a manifestation of friction-induced self-excited instability in disc brake systems. This study investigated non-smooth bifurcations and chaotic dynamics in disc brake systems and elucidated a chaotic control system. Decreasing squeal noise which is dependent on chaos, increases passengers comfort; consequently, suppressing chaos is crucial. First, synchronization was used to estimate the largest Lyapunov exponent to identify periodic and chaotic motions. Next, complex nonlinear behaviors were thoroughly observed for a range of parameter values in the bifurcation diagram. Rich dynamics of the disc brake system were studied using a bifurcation diagram, phase portraits, a Poincaré map, frequency spectra, and Lyapunov exponents. Finally, the proposed technique was applied to a chaotic disc brake system through the addition of an external input that is a dither signal. Simulation results demonstrated the feasibility of the proposed approach.
<Keywords: Disc brake; Synchronization; Nonlinear; Lyapunov exponent; Dither
Many practical engineering systems, where dry friction, clearance, and impact often cause sudden changes in the vector fields describing the dynamic behavior of the mechanical systems. Such systems are not smooth and are referred to as non-smooth dynamical systems. Dry friction is a typical non-smooth factor that is influential in engineering applications. These sources of self-sustained oscillations, which are referred to as stick-slip oscillations, often because undesired effects, such as the squeaking noise of automotive windshield wipers [1] and the squealing noise of brakes. In the automotive industry, brake squeal is a critical problem because it reduces customer satisfaction. Because vehicle quality standards are setting increasingly low thresholds for noise level and vibration, many researchers have intensively studied brake squeal, by using various analytical and experimental methods [2-7]. For example, after analyzing automotive disc brake squeal, Ouyang et al. [2] concludes that chattering behavior is a self-excited vibration based on a stick-slip phenomenon and that it is induced only in a certain range of friction parameters; this feature of the stick-slip phenomenon also occurs in other physical systems [8-11].
Despite the progress and insight gained in recent years, brake squealing still occures frequently. Dynamic behaviors of the disc brake system must be studied to find effective methods of controlling brake vibrations and squealing noises. Thus, disc brake noise generation and suppression are important considerations when designing and manufacturing brake components.
Brake squeal is a nonlinear transient phenomenon, and numerous analytical and experimental studies on brake systems have indicated that it can be treated as chaotic motion. For example, [12-14] showed that a forced two-degree-of-freedom (2-DOF) dry friction model with negative velocity gradient develops chaotic pad motion when the pad and disc are in close proximity. Numerical features, such as bifurcation diagrams, phase portraits, Poincaré maps, frequency spectra, and Lyapunov exponents can be used to study periodic and chaotic motions.
For a broad range of parameters, using Lyapunov exponents is the optimal approach for measuring the sensitivity of a dynamical system to its initial conditions. Lyapunov exponents can be used to determine whether a system is in chaotic motion, and the algorithms for computing the Lyapunov exponents of smooth dynamical systems are well established [15-18]. However, these algorithms are inapplicable to some non-smooth dynamical systems with discontinuities, such as those associated with dry friction, backlash, and impact. Although several methods for calculating the Lyapunov exponents of nonsmooth dynamical systems have been proposed [19-21], the method proposed by Stefanski [21] was applied in this study for estimating the largest Lyapunov exponent of a disc brake system.
Although some chaotic behavior is desirable, it is generally unwanted because it reduces the performance and operating range of many electrical and mechanical devices. Recent studies have considerably advanced control of a chaotic stick-slip mechanical system, and various new techniques have proposed [22-24]. For example, Galvanetto [22] applied adaptive control to unstable periodic orbits embedded in the chaotic attractors of some discontinuous mechanical systems, and Feeny and Moon [24] used high-frequency excitation, or dither, to quench stick-slip chaos.
In this study, chaos was successfully controlled by injecting another external input (i.e., a dither signal) into the system just ahead of the nonlinearity. The effectiveness of injecting dither signals to improve the performance of nonlinear elements is well established. For instance, Tsouri and Rootenberg [25] eliminated undesirable limit cycles in coupled-core reactor control systems, and Bambini and Stenholm [26], applied dither signals to a ring-laser gyroscope to compensate for the dead zone phenomenon caused by imperfections in optical glass.
These studies demonstrate the various practical applications of dither, which may be a signal or a mechanism. Because dither is an external signal and does not require measurements, its main advantage is simplicity. Dither has also been successfully applied in actual nonlinear systems [27-30]. For example, Fuh and Tung [27] used dither signals to convert chaotic motion to a periodic orbit in circuit systems.Liaw and Tung [28] used a dither smoothing technique to control noisy chaotic systems. Tung and Chen [29] presented an approach for identifying a closed-loop DC motor system with unknown parameters and nonlinearities; in addition, they investigated why dither signals eliminate possible limit cycles in the system. Furthermore, Chang et al. [30], used dither signals to suppress a chaotic permanent magnet in the synchronous motor of an electric vehicle.
To improve the performance of automotive disc brake systems and to eliminate chatter vibration, chaotic motion must be transformed to a periodic orbit in a steady state. In this study, chaos was successfully controlled by injecting an external input a dither signal into the system, which is an efficient method to improve the performance of nonlinear systems. Simulation results verified the efficiency and feasibility of the proposed method.
Figure 1 uses a 2-DOF model to illustrate the basic dynamics of brake squeal noise [13,14]. The systems with subscripts 1 and 2 represent the pad and the disc, respectively, and m, k, and c denote mass, stiffness, and damping, respectively. The motion of the first mass (m1) represents the tangential motion of the pad and that of the second mass (m2) represents the in-plane motion of the disc. The normal force acting on the interface is N=P×S where P is the applied pressure and S is the surface area of the interface. The resulting frictional force Ff depends on the normal force and the dynamic coefficient of friction between the two sliding surfaces. Disc motion is the superposition of constant imposed velocity v0 and velocity , and the velocity of the pad motion is
, and the velocity of the pad motion is 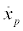 Stick motion is governed by a static friction force and slip motion is governed by a velocity-dependent friction force. In stick mode, the stick friction force is limited by the maximum friction force
Stick motion is governed by a static friction force and slip motion is governed by a velocity-dependent friction force. In stick mode, the stick friction force is limited by the maximum friction force 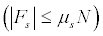 and is balanced by the reaction forces acting on the masses.μs is the static coefficient of friction and (Vr) is the dynamic coefficient of friction
and is balanced by the reaction forces acting on the masses.μs is the static coefficient of friction and (Vr) is the dynamic coefficient of friction 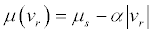 The relative velocity between the pad and the disc is vr. The negative gradient of the dynamic friction coefficient is a.
The relative velocity between the pad and the disc is vr. The negative gradient of the dynamic friction coefficient is a.
Considering relative motion between two masses, the static frictional force is
 (1)
(1)
Frictional force can be described as
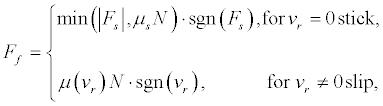 (2)
(2)
For numerical analysis, the frictional force is switched according to the motion, and a small region ε of the relative velocity is defined:  where
where  Thus, the equations of motion are
Thus, the equations of motion are
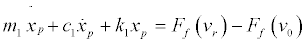 (3a)
(3a)
 (3b)
(3b)
where xp denotes the displacement variable of the pad and xd denotes the displacement variable of the disc, 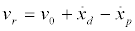 and the constant,
and the constant, 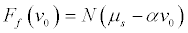 is introduced to compensate any offset. Let,
is introduced to compensate any offset. Let, 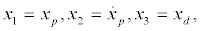 and
and 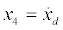 be the state variables such that the state equations of the friction model (Eqs. (3)) can be written as the following four first-order differential equations:
be the state variables such that the state equations of the friction model (Eqs. (3)) can be written as the following four first-order differential equations:

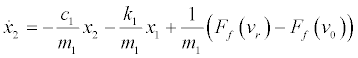

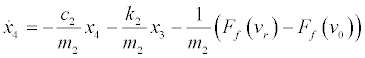 (4)
(4)
Table 1 presents the values of the parameters used in these equations [14].
| Parameter | Value |
|---|---|
| m1 | 1.0 |
| m2 | 1.0 |
| k1 | 1.0 |
| k2 | 3.0 |
| μs | 0.6 |
| v0 | 1.0 |
| N | 10.0 |
| a | 0.03 |
Table 1: Physical parameters of a disc brake system.
An indicator such as the largest Lyapunov exponent is one of the most useful diagnostic elements in any chaotic system. All dynamic systems have a spectrum of Lyapunov exponents (λ), which can be used to determine how length, area, and volume change in the phase space. In other words, Lyapunov exponents measure the rate of divergence (or convergence) of two initially nearby orbits. Chaos can be identified by simply calculating the largest Lyapunov exponent to determine whether nearby trajectories generally diverge (λ > 0) or converge (λ < 0). Any bounded motion in the system containing at least one positive Lyapunov exponent is defined as chaotic, whereas nonpositive Lyapunov exponents indicate periodic motion. Algorithms for computing the Lyapunov spectrum of smooth dynamic systems are well established [15-18]. However, these algorithms cannot be directly applied in discontinuous non-smooth dynamic systems such as dry friction, backlash, and stick-slip. In this study, the largest Lyapunov exponent was computed to describe chaotic behavior in an automotive disc brake system.
Recently, Stefanski [21] has recommended a simple method of estimating the largest Lyapunov exponent based on synchronization properties. Many recent studies have considered synchronization of two distinct systems, which structures may or may not be identical. Synchronization controls the response system by controlling the output of the drive system, such that the output of the response system asymptotically follows that of the drive system.
Stefanski’s method of estimating the largest Lyapunov exponent is briefly described herein [21].
The dynamic system is decomposed into the following two subsystems:
Drive system
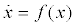 (5)
(5)
Response system
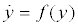 (6)
(6)
Consider a dynamic system comprising two identical n-dimensional subsystems, where the response system (6) is combined with a coupling coefficient d and the drive system (5) remains the same. Such a system can be expressed using the first-order differential equations as follows:
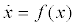
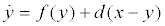 (7)
(7)
The synchronization condition (Eq. (7)) is
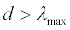 (8)
(8)
The smallest value of coupling coefficient d in synchronization ds is assumed to equal the maximum Lyapunov exponent, as follows:
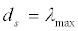 (9)
(9)
Eq. (7) yields the following augmented system based on Eq. (4):

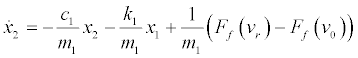
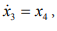
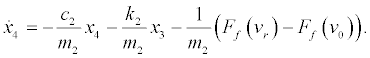
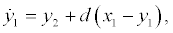
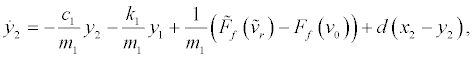
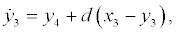
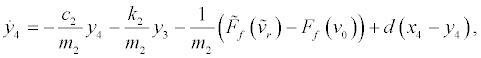 (10)
(10)
where
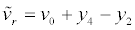
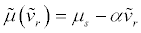

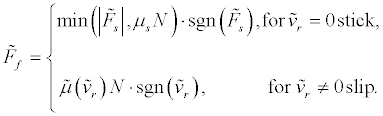 (11)
(11)
The next step determines the largest value of the Lyapunov exponent for the chosen parametric values according to the aforementioned method. Figure 2 presents the results of the numerical calculations required when using the described synchronization method to obtain the largest Lyapunov exponents. All the largest Lyapunov exponents are positive with respect to the damping coefficient (c1, c2) < 0.0168, which indicates chaotic motion. These calculations can be used to classify brake squeal mechanisms and to further elcuidate friction-related noise phenomena.
Disc brake system was characterized by performing numerical simulations according to Eq. (4); the simulations presented the dynamic behavior of the system over a range of parameter values as a bifurcation diagram, which is widely used to describe transitions from periodic to chaotic motion in dynamic systems. The commercial package DIVPRK of IMSL in the FORTRAN subroutine for mathematical applications was used to solve these ordinary differential equations [31]. Figure 3 presents the resulting bifurcation diagram, which clearly shows the chaotic motion in region III. Period-2n orbits appear in region II, and period-1 orbits occur in region I. A Poincaré map can be constructed by viewing the phase space diagram stroboscopically to reveal the periodic motion.
The phase portrait evolves from a set of trajectories emanating from various initial conditions in the state space. When the solution stabilizes, the asymptotic behavior of the phase trajectories is particularly interesting, and the transient behavior in the system can be ignored. Furthermore, a frequency spectrum can be used to differentiate between periodic, quasi-periodic, and chaotic motion in dynamic systems. A stable period-1 motion was observed in region I. Each response is characterized by a phase portrait, a Poincaré map (velocity vs. phase angle), and a frequency spectrum. Figure 4 illustrates that the periodic motion of Eq. (4) remains stable as long as the parameter (damping coefficient) falls within region I. When the parameter (damping coefficient) falls within region II, period-doubling bifurcations appear. Figure 5 presents the bifurcations resulting from the new frequency components at O/2, 3O/2, 5O/2, etc., which indicate that a cascade of period-doubling bifurcations can cause a series of subharmonic components. Figure 3 clearly shows that, when the parameter (damping coefficient) continues to decrease into region III, a cascade of period-doubling bifurcations causes chaotic motion. Chatter vibration and brake squeal can occur under these conditions.
The Poincaré map and frequency spectrum are two descriptors that can be used to characterize chaotic behavior. The Poincaré map presents an infinite set of points that are collectively referred to as a strange attractor. The frequency spectrum of chaotic motion covers a broad band. These two features of the strange attractor and the continuous type Fourier spectrum are strong indicators of chaos. Figure 3 shows that a period-doubling bifurcation occurring in region II eventually causes chaotic motion. The phase portrait, Poincaré map, and frequency spectrum in Figure 6 elucidate this behavior.
To improve the performance of a dynamic system, a chaotic system must be transformed to a periodic motion. This section describes how chaotic motion can be controlled by adding an external input, that is, a dither signal, to adjust only the nonlinear terms. A dither is a highfrequency signal introduced to modify system behaviors, mainly nonlinearity, in a nonlinear system. Because of its high frequency and periodic nature, a dither signal averages the nonlinearity. Dither smoothing techniques for stabilizing chaotic systems and widely used dither signals have been described [27,28,32].
The simplest dither signal is a square-wave dither, in which frequency and amplitude are 2000 rad/s and W, respectively, in front of the non-linearity f (y ± w). Consequently, the effective value of , the output of the nonlinear element, is
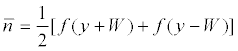 (12)
(12)
Therefore, the system equations are
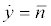 (13)
(13)
The simulation results have confirmed the effectiveness of the suggested method for suppressing chaos in an automotive disc brake system. To verify the efficiency of the proposed method, three damping coefficients have been selected from region III in Figure 3. In the absence of dither control, W = 0, Eq. (4) can be used to describe chaotic motion for damping coefficient c1 = c2 = 0.015. The effect of adding the square-wave dither control to the system given by Eq. (4) for the damping coefficient c1 = c2 = 0.015, have been also considered. By increasing the amplitude of the square-wave dither signal from W = 0 to 0.2 V, the dynamics change from chaotic behavior to periodic motion.
Figure 7 shows the evolution of the bifurcation diagram. Consider the disc brake system with the frictional force, i.e., the original nonlinearity f described by Eq. (2). The next steps are setting W = 0.15 V and plotting the effective nonlinearity n and original nonlinearity f in Figure 8. The time response of displacement is shown in Figure 9(a) where the squarewave dither signal is injected after 100 seconds. The chaotic behavior is converted into a period-one motion. Figure 9(b) is a phase portrait of the controlled system. Notably, the behavior of the system is chaotic but starts to be periodic after dither injection.
This study investigated complex nonlinear behaviors and the chaos control problem in a nonlinear automotive disc brake system. The system was characterized by numerical methods by using time responses, Poincaré maps, frequency spectra, and the largest Lyapunov exponent. The resulting bifurcation diagram showed many nonlinear dynamics and chaotic phenomena, and revealed that the disc brake system exhibited chaotic motion at low damping coefficients.
Nonlinear analysis by using a 2-DOF model demonstrated the rich nonlinear dynamics of the disc brake squeal noise and the importance of damping. The largest Lyapunov exponent a powerful tool for analyzing chaotic motion of the disc brake system was estimated from the properties of its synchronization phenomenon. These analytical results helped classify brake squeal mechanisms and further elucidate friction-related noise phenomena. Finally, a square-wave dither signal was used for efficient conversion of the chaotic system into a periodic orbit by injecting dither signals ahead of the nonlinearity of the chaotic system.
The proposed system can be used to model real disc brake systems in future studies. Figure 10 is a schema of the instrumentation used in the experimental study. The dither signal was supplied by a function generator with a frequency of 0-10000 Hz. Waveform analysis was performed using a HP 3562A dynamic signal analyzer. The analog signal was amplified by a voltage amplifier and servo amplifier that drove the DC motor. Studying the dynamics of automotive disc brake systems and controlling chaotic vibrations can enhance performance and prevent brake squeal noise.
The authors wish to thank the Ministry of Science and Technology of the Republic of China, Taiwan, for financially supporting this research under Contract No. MOST 104-2221-E-212-016 and NSC 102-2632-E-212-001-MY3.