Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2016) Volume 6, Issue 6
Nature of delocalization of the electrons from the ligands to metals in the first coordination sphere of the highspin complexes [Fe(H2O)6]2+/3+ and [Zn(H2O)6]2+ are computationally studied using density functional theory. Among the studied complexes, natural charge transfer from H2O ligands to metal ion is found to be maximum of 1.556e in [Fe(H2O)6]2+ and minimum of 0.621e in [Zn(H2O)6]2+. On the other hand, the interaction between the lone pairs of oxygen with metal ion is found to be stronger in [Zn(H2O)6]2+ than in the complexes with second coordination sphere. Number of such strong interactions in the first coordination sphere are found to be decreased with the addition of H2O ligands in the second coordination sphere.
<Keywords: Complex; Coordination sphere; Lone pairs; Natural charge; NBO; Delocalization
Metals are found in different forms in nature. One of the major forms is a molecule resulted from the coordination of metals with other molecules or ions. Such associations are often referred as coordination complexes [1]. These coordinated complexes play very important roles in the physiological activities of human and plant lives. For example, haemoglobin, a macromolecule responsible for the transportation of oxygen and carbon dioxide in blood, consists of coordination of iron with nitrogen bases around it [2]. Oxygen is transported by the first coordination sphere of the complex, whereas CO2 is transported by the second coordination sphere of the iron complex called heme. In plants, photosynthesis is carried out by the pigments called chlorophyll where coordination of magnesium with other molecules plays a vital role. Such prevalence of metal complexes indubitably make them a wide branch of study. The transition metal complexes are rich in structural diversity. Many successful computational study of aqua complexes have validated the outcomes of ab-initio methods using density functional theory. Structure and vibrational properties of the complexes [Fe(H2O)6]2+ and [Fe(H2O)6]2+ have been fastidiously studied by Jarzecki and co-workers [3] with DFT approach. The geometries of the complexes are precisely determined computationally at B3LYP level of approximation. With the same DFT approach the aqua complexes of Zn2+ ion have been studied by Rul´?sek? and Havlas [4]. Geometries of the complexes [Zn(H2O)6]2+ and [Ni(H2O)6]2+ have been calculated at B3LYP level of approximation using different basis sets ranging from 3-21G(d) to 6-311++G(d,p), and interaction energies have been determined by replacing water by one of the ligands CH3OH, CH3SH, or NH3 in the first coordination sphere. Varadwaj and co-workers [5] have studied the coordination chemistry of aqua complexes and mixed aqua-amine complexes in very detail to determine the geometry, ligands to metal charge transfer using UX3LYP level of approximation. These successful results have shed light on the reliability of the computational methods.
The structural diversity of the transition metal complexes is largely determined by the charge transfers between metals to surrounding molecules and vice-versa. Two types of charge transfers are prominent, Mulliken and Natural charge transfers. Among them, natural charge transfer has been opted as it explores the hybridization of the orbitals in the bond constituents. Metal orbitals form hybrid orbitals as the ligand orbitals do to form a bond. These hybrid orbitals are overlapped in the complexes to make it stable and this stability highly depends on the amount of charge exchange or transfer that take place between the ligands and metal ions [1]. In the present work we have comparatively studied the natural charge transfers in high-spin aqua complexes [Fe(H2O)6]2+=3+ and [Zn(H2O)6]2+. The change in the ligands to metal ion charge transfer in the first coordination sphere of the complex [Zn(H2O)6]2+ after adding one to four H2O in the second coordination sphere has also been studied. As [Zn(H2O)6]2+ is a closed shell system and [Fe(H2O)6]2+=3+ are open-shell systems, comparable but slightly different results are expected. The study of the transition metal complexes is now a wide branch of chemistry, physics, and biology as well. Any kind of careful study about these complexes may become fruitful for the advancement of the field.
Gaussian [6] program package was used to perform the calculations. Gaussian inputs of metal complexes were prepared and the outputs were visualized by using Gaussview 4.1.2. The geometries of the complexes were first optimized with different basis sets at the B3LYP level of approximation which merges Becke’s gradient-correlated exchange functional (B3) [7] and the Lee-Yang-Parr (LYP) [8]. The inputs were prepared by keeping the ligands in pseudo-octahedral geometry. Any restriction of symmetry was not imposed and the optimization were carried out with C1 point group symmetry. After the geometry optimization, frequency calculations were performed and global minima were confirmed. All of the calculations were performed by using the basis set 6-311+G(d) at B3LYP level of approximation. The loss of natural charge densities from the lone pairs of the oxygen atoms of the ligands H2O were studied by Natural Bond Orbital (NBO) analysis. NBOs give the direct insight to the nature of electronic conjugation between the bonds in the molecules. In the metal complexes, when the hybrid orbitals of the ligands are overlapped with the hybrid orbitals of the metal ions, delocalization of electrons take place. To figure our these delocalizations of the electrons, NBO analysis is a powerful tool. NBOs closely correspond to the picture of localized bonds and lone pairs as basic units of molecular structure, so that it is possible to conveniently interpret ab initio wave-functions in terms of the classical Lewis structure concepts by transforming these functions to NBO form [8]. The work is primarily focused on the results of second-order perturbation theory analysis of Fock matrix within NBO of the complexes. For each donor NBO (i) and acceptor NBO (j), the stabilization energy E(2) associated with delocalization is determined as [9].
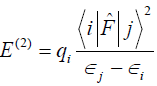
where qi is the donor orbital occupancy, ?i and ?j are the orbital energies, and F (i, j) is the off-diagonal NBO Fock matrix element. The larger the value of the E(2) the more intensive the interaction between the donors and acceptors [10].
The NBO partial charges on the metal ion Zn2+ and Fe2+/3+ and the charge transfer from the ligands to metal in the complexes [Zn(H2O)6]2+ and [Fe(H2O)6]2+/3+ are presented in the Table 1. Table 1 shows that the charge transfer has taken place from the ligands to metal ions in all cases. The degree of delocalization of the electrons of the lone pairs of oxygen as well as the metal orbitals are enumerated in the subsequent Tables. Among all interactions, only first two strongest interactions are mentioned in the Tables. The interaction of lone pairs of oxygen atom with the n* orbitals of metal is found to be the strongest in case of [Zn(H2O)6]2+ complex. In addition, the interaction of metal orbital with the virtual orbital is also found to be strongest in this complex (Figures 1-3). Table 2 shows that the delocalization of electrons from the lone pairs of oxygen to the n* orbitals of Zn2+ resulted in the strongest interaction of LP* O(5) with LP Zn with occupancy of 0.12384e stabilizing the complex [Zn(H2O)6]2+ by 47.20 kcal/mol. The interactions due to delocalization of electrons from the lone pair orbitals of oxygen atom to the n* orbitals of Fe2+ ion in the complex [Fe(H2O)6]2+ are present in the Table 3. It is seen in Table 3 that the interactions are weaker in [Fe(H2O)6]2+ than those in the complex [Zn(H2O)6]2+. The strongest interaction of LP O(2) with LP* Fe with occupancy of 0.08562e has stabilized the complex [Fe(H2O)6]2+ by 23.12 kcal/mol. The second strongest interaction is due to the delocalization of the electrons from the lone pairs of O(4) with LP* Fe with occupancy of 0.08562e which has been stabilizing the complex by 20.77 kcal/mol. Remaining all such interactions are found to be with E(2) less than 20 kcal/mol. A partial result of the the second-order perturbation theory analysis of Fock matrix within NBO of the complex [Fe(H2O)6]2+ at B3LYP/6-311+G(d) is presented in the Table 4. Two of the strongest interactions of lone pairs of oxygen with n* orbitals of Fe ion for each oxygen atom are mentioned in the table. Here the strongest interaction among all interactions is due to the delocalization of electrons from lone pairs of O(4) to the LP* Fe with occupancy 0.21613e resulting in E(2) equals to 20.32 kcal/mol. If the results of Tables 4 and 5 are compared, it is seen that when the contribution of the p orbital in the donor orbital is small, more amount of charge has been transferred from the metal ligands to the metal ions in case of the chosen iron complexes. The maximum charge transfer of 1.556e in the complex [Fe(H2O)6]2+ from the ligands to the metal ions confirms this fact. The most significant results of second-order perturbation theory analysis of Fock matrix within NBO of the complexes are presented in the Tables 6-9. In all of the cases only one stabilization energy due to delocalization of the electrons from the lone pairs of oxygen atoms in water ligands in the first coordination sphere to the n orbitals of Zn2+ is found to be greater than 4 kcal/mol. For this reason, only the strongest of all interactions are mentioned in these tables. For example, other interactions due to the delocalization of the electrons of LP O(5) in different RY* Zn orbitals have the values of E(2) equal to 0.09, 0.34, 0.07, 0.98, 0.99, 0.40, 2.58, 0.39, 1.14, 0.15, 0.29, 0.24, 0.69, 0.55, 2.63, 1.32, and 3.13 kcal/mol. Only the transfer of electrons from LP O(5) to LP Zn has stabilized the complex by 24.68 kcal/mol.
| Complex | QM (e) | Q (e) |
|---|---|---|
| [Zn(H2O)6]2+ | 1.379 | 0.621 |
| [Fe(H2O)6]2+ | 1.243 | 0.757 |
| [Fe(H2O)6]2+ | 1.444 | 1.556 |
Table 1: Natural charges on the metal ion QM and ligands-metal charge transfer Q in the complexes [Zn(H2O)6]2+, [Fe(H2O)6]2+ and [Fe(H2O)6]2+.
| Donor NBOs | occupancy (e) | hybrid | Acceptor NBOs | occupancy(e) | hybrid | E(2) (kcal/mol) |
|---|---|---|---|---|---|---|
| LP O (2) | 1.90290 | sp1.14 | LP* Zn | 0.24066 | sp0 | 27.35 |
| LP O (2) | 1.90290 | sp1.14 | LP* Zn | 0.12365 | sp1 | 27.48 |
| LP O (3) | 1.90282 | sp1.14 | LP* Zn | 0.24066 | sp1 | 27.40 |
| LP O (3) | 1.90282 | sp1.14 | LP* Zn | 0.12384 | sp1 | 47.18 |
| LP O (4) | 1.90291 | sp1.14 | LP* Zn | 0.24066 | sp0 | 27.34 |
| LP O (4) | 1.90291 | sp1.14 | LP* Zn | 0.12365 | sp1 | 27.39 |
| LP O (5) | 1.90282 | sp1.14 | LP* Zn | 0.24066 | sp0 | 27.39 |
| LP O (5) | 1.90282 | sp1.14 | LP* Zn | 0.12384 | sp1 | 47.20 |
| LP O (6) | 1.90288 | sp1.14 | LP* Zn | 0.24066 | sp0 | 27.38 |
| LP O (6) | 1.90288 | sp1.14 | LP* Zn | 0.12401 | sp1 | 28.20 |
| LP O (7) | 1.90274 | sp1.14 | LP* Zn | 0.24066 | sp0 | 27.42 |
| LP O (7) | 1.90274 | sp1.14 | LP* Zn | 0.12401 | sp1 | 28.26 |
Table 2: Results of second-order perturbation theory analysis of Fock matrix within NBO of the complex [Zn(H2O)6]2+.
| Donor NBOs | Occupancy (e) | Hybrid | Acceptor NBOs | Occupancy (e) | Hybrid | E(2) (kcal/mol) |
|---|---|---|---|---|---|---|
| LP O(2) | 0.93069 | sp1.11 | LP* Fe | 0.08562 | sp0d5.17 | 23.12 |
| LP O(2) | 0.93069 | sp1.11 | LP* Fe | 0.05902 | sp1d0 | 17.28 |
| LP O(3) | 0.92739 | sp1.14 | LP* Fe | 0.08827 | sp0d0.21 | 14.30 |
| LP O(3) | 0.92739 | sp1.14 | LP* Fe | 0.06108 | sp1d0 | 13.90 |
| LP O(4) | 0.93159 | sp1.11 | LP* Fe | 0.08562 | sp0d5.17 | 20.77 |
| LP O(4) | 0.93159 | sp1.11 | LP* Fe | 0.05901 | sp0d5.17 | 17.70 |
| LP O(5) | 0.92766 | sp1.14 | LP* Fe | 0.08827 | sp0d0.21 | 14.17 |
| LP O(5) | 0.92766 | sp1.14 | LP* Fe | 0.06108 | sp1d0 | 13.67 |
| LP O(6) | 0.92875 | sp1.12 | LP* Fe | 0.08827 | sp0d0.21 | 17.43 |
| LP O(6) | 0.92875 | sp1.12 | LP* Fe | 0.06108 | sp1d0 | 11.66 |
| LP O(7) | 0.92832 | sp1.12 | LP* Fe | 0.08827 | sp0d0.21 | 17.34 |
| LP O(7) | 0.92875 | sp1.12 | LP* Fe | 0.06108 | sp1d0 | 11.83 |
Table 3: Results of second-order perturbation theory analysis of Fock matrix within NBO of the complex Fe(H2O)6]2+.
| Donor NBOs | Occupancy (e) | Hybrid | Acceptor NBOs | Occupancy (e) | Hybrid | E(2) (kcal/mol) |
|---|---|---|---|---|---|---|
| LP O(2) | 0.90736 | sp9.1 | LP* Fe | 0.21613 | sp0d1 | 20.21 |
| LP O(2) | 0.90736 | sp9.1 | LP* Fe | 0.12644 | sp0d0 | 18.75 |
| LP O(3) | 0.90719 | sp9.1 | LP* Fe | 0.12644 | sp0d0 | 18.85 |
| LP O(3) | 0.90719 | sp9.1 | LP* Fe | 0.21631 | sp0d1 | 11.45 |
| LP O(4) | 0.90708 | sp9.1 | LP* Fe | 0.21613 | sp0d1 | 20.32 |
| LP O(4) | 0.90714 | sp9.1 | LP* Fe | 0.12644 | sp0d0 | 18.86 |
| LP O(5) | 0.90736 | sp9.1 | LP* Fe | 0.12644 | sp0d0 | 18.75 |
| LP O(5) | 0.90736 | sp9.1 | LP* Fe | 0.21631 | sp0d1 | 11.43 |
| LP O(6) | 0.90734 | sp9.1 | LP* Fe | 0.21631 | sp0d1 | 19.68 |
| LP O(6) | 0.90734 | sp9.1 | LP* Fe | 0.12644 | sp0d0 | 18.94 |
| LP O(7) | 0.90694 | sp9.0 | LP* Fe | 0.21631 | sp0d1 | 19.69 |
| LP O(7) | 0.90694 | sp9.0 | LP* Fe | 0.21631 | sp0d1 | 19.69 |
Table 4: Results of second-order perturbation theory analysis of Fock matrix within NBO of the complex [Fe(H2O)6]2+.
| Complex | QZn (e) | DQ (e) |
|---|---|---|
| [Zn(H2O)6](H2O)2+ | 1.736 | 0.264 |
| [Zn(H2O)6](H2O)22+ | 1.735 | 0.265 |
| [Zn(H2O)6](H2O)32+ | 1.732 | 0.268 |
| [Zn(H2O)6](H2O)42+ | 1.731 | 0.269 |
Table 5: Natural charge on the metal ion QZn and ligands to metal charge transferΔQ in the complexes [Zn(H2O)6](H2O)2+ n=1-4.
Table 6 summarises the strongest stabilization energy values of all oxygen atoms. Among them, the strongest interaction is the one where electrons from the lone pairs of O(2) are delocalized in the LP* with occupancy 0.24310e. This is the oxygen atom of water ligand in the first coordination sphere where one ligand in the second coordination sphere is attached. In the Table 7, it is seen that there are two highest values of E(2) closer to each other. One is due to the delocalization of the electrons from the lone pairs of O(2) to the LP Zn with occupancy 0.24430e and another is due to the delocalization of the electrons from the lone pairs of O(4) to the metal orbital. These are the oxygen atoms of water ligands in the first coordination sphere on which the ligands in the second coordination sphere are attached. Table 8 shows that in the complex 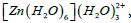 the strongest interaction is due to the delocalization of the electrons from the lone pairs of O(4) to the LP Zn with occupancy 0.24699e which has stabilized the complex by 29.29 kcal/mol. This is the oxygen atom of water ligand in the first coordination sphere lying closest to the Zn2+ ion. All of the strongest interactions are found to be due to the delocalization of the electrons to the same n* Zn orbitals from the lone pair orbitals of oxygen atom in the first coordination sphere. Finally, Table 9 presents the interactions with maximum E(2). In the complex
the strongest interaction is due to the delocalization of the electrons from the lone pairs of O(4) to the LP Zn with occupancy 0.24699e which has stabilized the complex by 29.29 kcal/mol. This is the oxygen atom of water ligand in the first coordination sphere lying closest to the Zn2+ ion. All of the strongest interactions are found to be due to the delocalization of the electrons to the same n* Zn orbitals from the lone pair orbitals of oxygen atom in the first coordination sphere. Finally, Table 9 presents the interactions with maximum E(2). In the complex 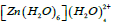 as seen from the table, the strongest interactions are due to the delocalization of the electrons from the lone pairs of O(2) and O(4). These are the two atoms of the water ligands present in the first coordination sphere lying closest to the Zn2+ ion and on which the water ligands in the second coordination sphere are attached.
as seen from the table, the strongest interactions are due to the delocalization of the electrons from the lone pairs of O(2) and O(4). These are the two atoms of the water ligands present in the first coordination sphere lying closest to the Zn2+ ion and on which the water ligands in the second coordination sphere are attached.
| Donor NBOs | Occupancy (e) | Hybrid | Acceptor NBOs | Occupancy (e) | Hybrid | E(2) (kcal/mol) |
|---|---|---|---|---|---|---|
| LP O(2) | 1.94302 | sp1.29 | LP* Zn | 0.24310 | sp0 | 30.60 |
| LP O(3) | 1.95802 | sp1.10 | LP* Zn | 0.24310 | sp0 | 24.72 |
| LP O(4) | 1.95681 | sp1.11 | LP* Zn | 0.24310 | sp0 | 24.74 |
| LP O(5) | 1.95811 | sp1.10 | LP* Zn | 0.24310 | sp0 | 24.68 |
| LP O(6) | 1.95843 | sp1.10 | LP* Zn | 0.24310 | sp0 | 24.35 |
| LP O(7) | 1.95641 | sp1.22 | LP* Zn | 0.24310 | sp0 | 25.20 |
Table 6: Results of second-order perturbation theory analysis of Fock matrix within NBO of the complex [Zn(H2O)6](H2O)2+.
| Donor NBOs | Occupancy (e) | Hybrid | Acceptor NBOs | Occupancy (e) | Hybrid | E(2) (kcal/mol) |
|---|---|---|---|---|---|---|
| LP O(2) | 1.94480 | sp1.27 | LP* Zn | 0.24430 | sp0 | 29.20 |
| LP O(3) | 1.96010 | sp1.10 | LP* Zn | 0.24430 | sp0 | 23.90 |
| LP O(4) | 1.94474 | sp1.27 | LP* Zn | 0.24430 | sp0 | 29.24 |
| LP O(5) | 1.96012 | sp1.10 | LP* Zn | 0.24430 | sp0 | 23.89 |
| LP O(6) | 1.99822 | sp1.00 | LP* Zn | 0.24430 | sp0 | 22.31 |
| LP O(7) | 1.95748 | sp1.1 | LP* Zn | 0.24430 | sp0 | 25.24 |
Table 7: Results of second-order perturbation theory analysis of Fock matrix within NBO of the complex [Zn(H2O)6](H2O)22+.
| Donor NBOs | Occupancy (e) | Hybrid | Acceptor NBOs | Occupancy (e) | Hybrid | E(2) (kcal/mol) |
|---|---|---|---|---|---|---|
| LP O(2) | 1.94831 | sp1.26 | LP* Zn | 0.24699 | sp0 | 27.27 |
| LP O(3) | 1.96093 | sp1.31 | LP* Zn | 0.24699 | sp0 | 22.93 |
| LP O(4) | 1.94358 | sp1.39 | LP* Zn | 0.24699 | sp0 | 29.29 |
| LP O(5) | 1.96086 | sp1.28 | LP* Zn | 0.24699 | sp0 | 23.07 |
| LP O(6) | 1.95862 | sp1.13 | LP* Zn | 0.24699 | sp0 | 24.43 |
| LP O(7) | 1.95376 | sp1.32 | LP* Zn | 0.24699 | sp0 | 25.97 |
Table 8: Results of second-order perturbation theory analysis of Fock matrix within NBO of the complex 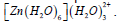
| Donor NBOs | Occupancy (e) | Hybrid | Acceptor NBOs | Occupancy (e) | Hybrid | E(2) (kcal/mol) |
|---|---|---|---|---|---|---|
| LP O(2) | 1.94489 | sp1.39 | LP* Zn | 0.24815 | sp0 | 28.85 |
| LP O(3) | 1.96281 | sp1.36 | LP* Zn | 0.24815 | sp0 | 21.97 |
| LP O(4) | 1.94490 | sp1.39 | LP* Zn | 0.24815 | sp0 | 28.85 |
| LP O(5) | 1.94463 | sp1.36 | LP* Zn | 0.24815 | sp0 | 21.99 |
| LP O(6) | 1.95879 | sp1.12 | LP* Zn | 0.24815 | sp0 | 24.49 |
| LP O(7) | 1.95048 | sp1.37 | LP* Zn | 0.24815 | sp0 | 27.42 |
Table 9: Results of second-order perturbation theory analysis of Fock matrix within NBO of the complex 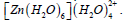
Nature of hybridization and charge transfer in the metal complexes 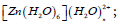 n=0-4 and [Fe(H2O)6]2+/3+ using natural bond orbitals has been successfully studied. Ligands to metal natural charge transfer is found to be maximum in [Fe(H2O)6]3+ among [Zn(H2O)6]2+ and [Fe(H2O)6]2+/3+. In [Zn(H2O)6]2+, this natural charge transfer is significantly reduced to 0.264e from 0.621 with the addition of one H2O in the second coordination sphere. However, it is increased slightly when the number of H2O ligands in the second coordination sphere is increased. In case of the complex [Zn(H2O)6]2+ and [Fe(H2O)6]2+, hybridization in donor NBOs are uniform. In case of the complex [Zn(H2O)6]2+, changes in different bond lengths have taken place with the addition of water in the second coordination sphere. It is found that whenever the oxygen atoms of water in the first coordination sphere approaches the metal ions, the contributions of p orbital in the hybrid orbitals increase. These changes in bond lengths have brought changes in the values of stabilization energy E(2). Mocking these structures can be intensified by increasing the number of ligands surrounding the first coordination sphere of the complexes. This will be fruitful in generalizing the findings of this work. Every attempt in doing so may significantly produce accurate and useful results in future.
n=0-4 and [Fe(H2O)6]2+/3+ using natural bond orbitals has been successfully studied. Ligands to metal natural charge transfer is found to be maximum in [Fe(H2O)6]3+ among [Zn(H2O)6]2+ and [Fe(H2O)6]2+/3+. In [Zn(H2O)6]2+, this natural charge transfer is significantly reduced to 0.264e from 0.621 with the addition of one H2O in the second coordination sphere. However, it is increased slightly when the number of H2O ligands in the second coordination sphere is increased. In case of the complex [Zn(H2O)6]2+ and [Fe(H2O)6]2+, hybridization in donor NBOs are uniform. In case of the complex [Zn(H2O)6]2+, changes in different bond lengths have taken place with the addition of water in the second coordination sphere. It is found that whenever the oxygen atoms of water in the first coordination sphere approaches the metal ions, the contributions of p orbital in the hybrid orbitals increase. These changes in bond lengths have brought changes in the values of stabilization energy E(2). Mocking these structures can be intensified by increasing the number of ligands surrounding the first coordination sphere of the complexes. This will be fruitful in generalizing the findings of this work. Every attempt in doing so may significantly produce accurate and useful results in future.
Our sincere gratitude to Associate Professor Dr. Rajendra Parajuli from the Department of Physics, Amrit Campus for all the suggestions he provided. We would like to extend this gratitude to Central Department of Physics, Tribhuvan University for providing Gaussian 03 suite of program. We are also thankful to Ms. Astha KC for the support during calculations and Mr. Mangesh Bhattarai from IIT, Guwahati for his valuable suggestions and support.