MD: Molecular Dynamics; BPTI: Bovine Pancreatic Trypsin Inhibitor; FDBP: Finite Differences Poisson-Boltzmann; FEP: Free Energy of Perturbation; NVT: Number of molecules/atoms in assemby, Volume, Temperature; NPT: Number of molecules/atoms in assembly, Pressure, Temperature; NVE: Number of molecules/atoms in assembly, Volume, Energy; PBC: Periodic Boundary Conditions; PDB: Protein Data Bank; PDLD: Protein Dipole-Langevin Dipole; PTP1B: Protein-Tyrosine Phosphatase 1B; QM/MM: Quantum Mechanics/ Molecular Mechanics;RMSD: Root Mean Sqared Displacement; Force fields; AMBER: Assisted Model Building with Energy Refinement; CHARMM: Chemistry at Harvard Macromolecular Mechanics; GROMOS: Groningen Molecular Simulation force field; OPLS-AA: Optimized Potentials for Liquid Simulations-all atoms; Water models; SPC/E flexible: Simple Point Charge 3-site water model (/E extended with average polarization correction to the potential energy function); TIP3P/4P/5P: Transferable Intermolecular Potential 3/4/5-site water models

MD methods were originally devised within the theoretical physics community during the 1950s and in 1957 when Alder and Wainwright [1] performed the first MD simulation using a hard-sphere model. The first macromolecular simulation, of BPTI, was done in 1975 with a crude molecular mechanics potential, and lasted for only 9.2 ps [2]. MD simulations mimic the physical motions of atoms in the protein molecule present in the actual environment. The atoms are allowed to interact for a certain period of time, which will help to compute their trajectory in and around the protein molecule. Simulation provides great detail of information about individual motion of atoms as a function of time. The potentials used in simulation procedures are approximate and under the control of the user by removing and altering specific contribution terms, their role in determining a given property can be examined.

Molecular Mechanics force fields are the cornerstone of biomolecular simulations, being used to compute the potential energy of a system of particles. The role of solvent is very important in simulation to determine the internal motion [3] of proteins at different temperatures, particularly below the glass transition [4] temperature, since experimentally it may be sometimes difficult to capture the dynamics associated with the internal motion of proteins. Molecular dynamics simulations provide connection between structure and dynamics by enabling the study of the conformational energy landscape accessible to protein molecules [5]. In recent years, some widely used MD simulation packages such as NAMD [6], GROMACS [7], and AMBER [8], have all substantially improved their algorithmic sophistication and parallel performance, being able to deliver up to ~10-100 ns/day/workstation/cluster [9]. MD simulation provides an alternate approach to the study of protein dynamics at NMR relaxation time scales. MD simulation studies are done at NMR timescales to calculate order parameter [10] and residual dipolar coupling [11] of proteins. Residual dipolar coupling provides information about the relative orientation of the parts of the protein that are present far apart in the structure. NMR spectroscopy enables the measurement of order parameters that gives an atomistic description of fluctuations in protein structure over pico- and nanoseconds [12]. Contrast between NMR spectroscopy and MD simulations can be used to interpret experimental results [13] and to improve the quality of simulationrelated force fields and integration methods [14]. Over time a large number of ingenious alternative approaches to classical MD simulation have been developed such as Monte-Carlo sampling of conformational space, simulated annealing, steered MD, hybrid Quantum Mechanics/ Molecular Mechanics (QM/MM), coarse-grained dynamics, Brownian dynamics, normal vibration modes analysis, molecular docking simulations and other non-dynamic methods, all leading to spectacular applications and developments in biomolecular simulation.

Force fields provide information about the potential energy of a system of particles. Force field parameters are obtained from experimental and quantum mechanical studies of small molecules, and it is postulated that such parameters may be transferred to desired larger molecules. Force field function comprises bonded and non-bonded interaction terms. Bonded interactions include harmonic oscillator energy of bond lengths, bond angles, and sometimes improper dihedrals (hard terms) and torsional dihedral angles (soft terms, sometimes including improper dihedrals), while Van der Waals interactions and electrostatic interactions contribute to non-bonded interactions. It is worth mentioning that Van der Waals interaction terms, described by a Lennard-Jones (6-12) potential function, include only dispersion or London interactions between transient dipoles, while Keesom interactions (between permanent dipoles) and Debye (induced dipole) interactions are included in the electrostatic (Coulomb) term, without explicit development into charge distribution momenta. Following is the most widely used energy function [15] [Manual for the Molecular Dynamics Package Q, v5.0 http://xray.bmc.uu.se/~aqwww/q/]:

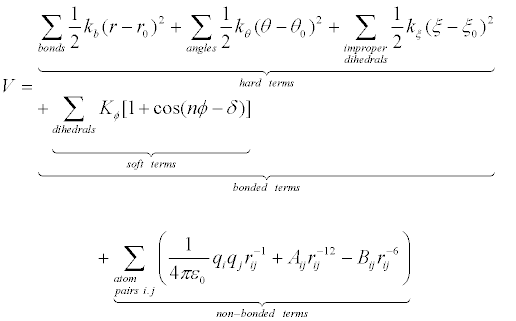(1)

In equation 1, potential energy V is a function of the Cartesian coordinate set R, specifying the positions of all atoms, from which the internal coordinates for bond lengths (r), bond angles (θ), dihedral angles (ϕ) and interparticle distances (r_ij) are calculated. There are multiple force fields available, and selection of the most adequate force field for a specific application is essential in simulation studies. For biomolecular simulations widely used molecular force fields include AMBER03 [16], AMBER94 [17], AMBER96 [18], CHARMM27 [19], OPLS-AA [20], GROMOS87 [21], GROMOS96 [22].

There are multiple steps involved in simulation and Figure 1 shows some of the most important ones. MD simulation starts with the knowledge of the potential energy of the system with respect to its position coordinates. The first derivative of the potential function to the position coordinates helps to compute the force acting on individual atoms of the system. The essential steps involved in the MD simulations of proteins are as follows.

Figure 1: Flow chart depicting steps involved in MD simulation of a protein.

Simulation environment

Protein simulation is done to replicate the experimental conditions, so several parameters for the different physical conditions are considered (such as pressure, temperature). In general the protein simulation is done in canonical ensemble (NVT), particularly the initial equilibration steps, or isothermal-isobaric (NPT) ensemble. For simulation, the protein molecules should be kept in the unit cell and solvated with explicit solvent. There is a broad range of explicit water models available and most popular of these models include TIP3P, TIP4P [23], TIP5P [24], SPC, and SPC/E [25]. The aforementioned water models are determined by Quantum mechanics-driven Molecular mechanics and validated by experimental methods. Water models are used to imitate the specific nature and complexity of molecule hydration, including orientation of solvent dipoles and effective electrostatic shielding, subtle hydrogen bond network rearrangements, clathration of hydrophobic surfaces, and accompanying changes in entropy. Unfortunately, due to limited time resolution of MD simulations and the intricate quantum nature of hydrogen bonds, most simulation environments do not treat them explicitly, including instead an average energy contribution to the non-bonded terms and using shake algorithms for solvent hydrogens repositioning. On the other hand, the use of implicit solvent models seeks to approximate the solute potential of the mean force, which determines the statistical weight of solute conformations, and is obtained by averaging over the solvent degrees of freedom [26]. To avoid polarization of the simulation ensemble, the total charge of the system should be kept zero by replacing certain solvent molecules with ions. To avoid interaction problems at system boundary, constrained spherical boundary models for solute and solvent can be applied, with specific corrections for density and polarization effects or the highly popular approach of cubic or rectangular periodic boundary conditions (PBC) consisting of repetitions of the system in the 26 adjacent unit cells. When a molecule leaves the system on one side, its equivalent image enters from the adjacent system on the opposite side, leading to conservation of mass and number of particles. Molecules within image systems are used for computation of long-range non-bonded interactions, and the Ewald summation has been directly applied in standard solvated periodic boundary simulations of biomolecular systems to compute the electrostatic interaction in the system [27].

Energy minimization

This step involves finding the global minimum energy with respect to the position of side chains atoms that represents the geometry of the particular arrangements of atoms in which the net attractive force on each atom reaches a maximum. There are various methods to compute the minimum energy but most widely used methods are steepest descent and conjugate gradient. Steepest descent method is one of several first-order iterative descent methods and utilizes the gradient of the potential energy surface. It directly relates to the forces in the Molecular mechanical description of molecular systems, to guide a search path toward the nearest energy minimum [28]. An essential issue is correcting the protonation state of titratable residues. This task can be performed using either free energy of perturbation (FEP) MD simulations or with continuum electrostatics models such as finite differences Poisson-Boltzmann (FDPB) or protein dipole-Langevin dipole (PDLD).

Heating the system and equilibration

In heating phase, initial velocities (at 0 K) are assigned to each atom of the system during energy minimization and Newton’s equations of motion that represent the time evolution of system are numerically integrated. At short predefined intervals, new velocities are assigned corresponding to a slightly higher temperature and the simulation is allowed to continue until desired temperature is achieved. Force constrains on different subdomains of the simulation system are gradually removed as structural tensions dissipate by heating. Thermalization is usually performed at constant volume with Langevin dynamics.

Equilibration stage is used to equilibrate kinetic and potential energies means distribute the kinetic energy “pumped” into the system during heating among all degrees of freedom. In explicit solvent simulation, protein positions are fixed and waters move accordingly. Once the solvent is equilibrated, the constraints on the protein can be removed and the whole system (protein + solvent) can evolve in time.

Production phase

Production phase is the last step of the simulation methodology to remove constraints on protein. It is carried out for desired time scale to generate trajectory of protein molecule in compliance with particular equilibrium conditions such as NVT, NPT and NVE. The timescale can be varied from several hundred picoseconds to microseconds or more. To avoid large trajectory artifacts during long runs, a 2D grid correction map of backbone ϕ and ψ parameters obtained from alanine, proline and glycine dipeptide surfaces (CMAP correction) has been included in more recent versions of CHARMM protein parameter files.

Analysis

In this step, stored coordinates and velocities of the system are used for further analysis. MD simulations can help to visualize and understand conformational changes at an atomic level when combined with visualization software which can display the structural parameters of interest in a time dependent way. MD simulation routinely calculates the following quantities 1) Time average structure 2) Radius of Gyration 3) Total energy of system 4) RMSD difference between two structures 5) interface related terms like order parameter, density of groups, electrostatic potential [29] . As an example we present a 3-nanosecond MD simulation of Protein-tyrosine phosphatase 1B (PTP1B) and inhibitor SNA complex [30]. Figure 2A shows that the total energy of PTP1B complexed with inhibitor decreases more sharply, and Figure 2B shows that the energy of uncomplexed PTP1B does not change too much. Root mean square deviation (RMSD) values of PTP1B (uncomplexed) and PTP1B-inhibitor (complexed) become stabilized after 1700 ps and 500 ps equilibrations, as shown in Figure 3. There is larger fluctuation in Radius of gyration in uncomplexed PTP1B relative to PTP1B complexed with inhibitor, as shown in Figure 4.

Figure 2: Total energy of (A) the uncomplexed PTP1B and (B) PTP1B-SNA complex as a function of simulation time for 3 –ns MD simulation. Reproduced with permission from Nature Publishing Group Copyright @ 2006

Figure 3: Time dependence of the RMS deviation from the crystal structure of the uncomplexed PTP1B (black) and the PTP1B-SNA complex (red) for all atoms over the 3-ns MD simulation. Reproduced with permission from Nature Publishing Group Copyright @ 2006

Figure 4: Radius of gyration as a function of time of uncomplexed PTP1B (black) and the PTP1B-SNA complex (red) during individual 3-ns MD simulation. Reproduced with permission from Nature Publishing Group Copyright @ 2006

In the current scenario, advancement in algorithms of MD simulation and computational facilities helps us to explore bigger biological systems for a longer timescale. A typical simulation of system size about 10⁵-10⁶ atoms for several nanoseconds simulation will probably require 10⁶ -10⁷ time steps and is expected to take a couple of days on workstation/cluster. During the period of simulation run it produces gigabytes of data for further analysis and visualization. Simulation analysis with visualization software enables investigation of motions and conformational changes that have functional inference and yields information that is not available through any other means. MD simulation results can be validated by protein dynamics by NMR and use to improve parameterization of the force fields. MD simulations yield great level of information but the challenge is to establish its validation. Molecular Dynamics simulation is more effective when it is coupled with experimental results on protein function at routinely basis, which play an essential role in validating and improving the simulations [31].

SP and DC gratefully acknowledge the IISER-BHOPAL team for research facilities and infrastructure.