Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Review Article - (2025)Volume 14, Issue 2
This paper presents a detailed overview about the modelling of hypersonic flows and their applications like scramjets and detonation phenomenon. The computational analysis of a wedge as well as blunt shaped 2D re-entry vehicle was carried out in order to compare the drag. Also, the aerodynamic properties were studied for re-entry vehicle at different mach numbers. Various turbulence models were used to compare the hypersonic simulations. In the application part, NASA Hyper X-43A scramjet geometry was used a s a reference geometry and the throat areas of the combustion chamber section were used by 1.4 and 2.8 times respectively in order to improve the thrust and specific impulse. Two spike shaped struts were used as fuel injectors and simulations were carried out at different mach numbers. Simulations were also carried out for the outer section of NASA Hyper X-43A scramjet vehicle. For the detonation phenomenon, a single wedge shaped fuel injector was used for checking the stability of detonation waves and comparing it with deflagration.
Hypersonic flows; Fuel injector; Hypersonics; Rareified gas dynamics
The physics used to simulate these turbulent flows is provided by the Navier-Stokes equations. Additional conditions must be provided in addition to the standard inlet, outlet and wall conditions in order to perform simulations for any kind of turbulent flow. The additional parameters consist of the rate of freestream dissipation, the thickness of the boundary layer formed and the intensity of the turbulence. One of the main obstacles to verifying these simulations is that the boundary layer's thickness cannot be obtained through hypersonics. With the aid of the codes and an examination of the grid's convergence for the intended geometry, the numerical accuracy can be verified. When analyzing grid convergence, discretization error is a key factor. What separates the accurate solutions of partial differential equations from the difference equations is what matters
Rareified gas dynamics
As the Poissulle equations failed to hold above a certain pressure limit, the need for riefied gas dynamics emerged. Knudsen number, which is dependent on the mean free path of the molecules, is a characteristic of this field of gas dynamics. This Knudsen number's extremely low values indicate the flow's hydrodynamic basis. Medium and large Knudsen numbers, which indicate transition and free-molecular nature, respectively, are calculated using the direct monte carlo simulation method. The inversely proportional rarefaction parameter to the Kunsen number must also be taken into account. A velocity distribution function was used to calculate the macro properties like pressure, stress tensor, temperature and many more. These distribution functions were satisfying the Bolzman’s equation [1].
Modelling of turbulence in hypersonic flows
For biconic vehicle heat prediction in hypersonic flows, Shutian Yu, et al. proposed a CFD modeling strategy. To make the number of cells reliant on the first layer's density, they maintained the height of the first cell and the expansion ratio simultaneously. For modeling the turbulence of the hypersonic flows, they employed various solvers. Kinematic viscosity, the sole variable in the Spallart Alamars model, is expressed in a single equation. Two equations that further alter the eddy viscosity provided by Spallart Alamaras are presented as part of the SST k-w model. Changes in the grid size had no effect on the contours of pressure and temperature. However, it was found that the heat flux varied with grid size, particularly close to the stagnation point. The wall cell Reynolds number of 1 corresponded to the highest accuracy of the heat transfer rate and any value greater than 16 resulted in very low accuracy. Furthermore, they noted that the accuracy increase ceased after three million cells. Generally speaking, the vehicle's highest temperature is reached at the leading edge stagnation point. Here is where an accurate temperature prediction becomes crucial to maintaining the vehicle in a safe condition.
When the hypersonic mach number is attained at higher altitudes, non-equilibrium hot spot regions form. The Monte Carlo relations model these regions. Intermolecular collisions are what keep the gas's equilibrium stable. When both the density and the length scale decrease, non-equilibrium regions are created. The mean free path increases and both viscosity and thermal conductivity cannot be transported at a Knudsen number close to zero. The current methods to simulate these flows break down as the Knudsen number rises above 0.01.
Shock-boundary layer interaction
A work on modeling hypersonic flows with equilibrium and non-equilibrium regimes was presented by Wenqing Zhang, et al. Thermal and chemical characteristics can also be used to categorize these regimes. At lower altitudes, the equilibrium regimes occur with a higher density. The Knudsen number serves as a defining feature of them. Because this condition forms the equilibrium flow regime, hypersonic flow modeling uses Navier-Stokes equations if the Knudsen number is less than 0.001. For modeling, the non-equilibrium Navier-Stokes equations are applied when the flow lies between the 0.001 and 0.1 Knudsen numbers. Additionally, there are no slip boundary conditions used because this regime cannot accurately predict properties like shear stresses and heat flux [2].
Boltzmans equation is used for mentioning all the microscopic phenomenon of the flow. Two methods are used for the solving of these equations namely DSMC and discrete velocity method. DSMC follows the approach of particle while DVM solves the equations directly. The flow which occurs at lower altitude within 4 km is referred to as thermochemical flow. This flow uses single temperature model for solving of governing equations. The authors have also mentioned various methods for lowering the Gibbs free energy.
Non-equilibrium flows use the non-equilibrium Navier-Stoke’s equations for modelling which consist of two temperatures as well as three temperature models also. These additional temperatures are vibrational temperature and electronic energy temperature. The two temperature model assumes both above temperatures are same. The no-slip boundary conditions near the wall fail for this regime as the momentum transfer near the wall is not same, so the temperature and velocity near the wall is not same as that of flow. The molecules and ions formed due to the occurrence of shock can come together again to release high amount of energy which can act as aerothermal load or aerodynamic heating making disadvantage for the vehicle.
Every microscopic phenomenon related to the flow is mentioned using Boltzman's equation. The discrete velocity approach and the DSMC are the two techniques used to solve these equations. Although DVM solves the equations directly, DSMC uses a particle approach. Thermal chemical flow is the term used to describe the flow that happens within 4 km at lower altitudes. Here, the governing equations are solved using a single temperature model. A number of techniques for reducing the Gibbs free energy have also been mentioned by the authors.
Hypersonic modelling of ballistic missiles
S. C. Lean and J. D. Teare studied various hypersonic parameters in addition to the chemical rates dot the strength of the bow shock waves that these stream tubes are passing through determines how many stream tubes are formed out of an inviscid flow. By integrating the chemical rate equation behind the shock, one can find the functions of temperature, density and many other chemical parameters. In terms of distance, these parameters can be found. We use iterative methods to calculate the pressure distribution in the hypersonic flow. The flows that can take into consideration the equilibrium pressure are those that resemble equilibrium conditions. The chemistry, however, will play a very minor part in the frozen flows. For leading-edge bodies with sharp edges, it is imperative to compute the pressure distributions by subtracting the equilibrium pressure distributions from the frozen conditions. Given that it is extremely rapid; this expansion adheres to the Prandtl-Meyer expansion method. Conversely, for the blunt-shaped bodies, expansion occurs gradually.
The area of the stream tube cross section was computed using the continuity equation after the density and velocity distributions were taken into account. This will reveal the location of the outermost active stream tube. The solid boundary is established by taking normal shockwaves close to the stagnation point into consideration. Consequently, even though we took into account approximative parameters with errors, the values of the initial pressure distributions in the hypersonic flows come out precisely. and the boosters that were employed. Because of the body's blunt shape, the wake region was forming behind the body and the flow was separating. Furthermore, because the hammerhead was blunt, self-excited oscillations were beginning to form.
Traditional method of modelling of hypersonic flow over missiles
S.C. Lean and J.D. Teare conducted a study on various hypersonic parameters and chemical rates. The inviscid flow was divided into multiple stream tubes based on the strength of the bow shock waves they passed through. The functions of temperature, density and other chemical parameters were determined by integrating the chemical rate equation behind the shock. These parameters were expressed in terms of distance. Pressure distribution in hypersonic flow was calculated using iterative methods. Flows resembling equilibrium situations considered equilibrium pressure, while the role of chemistry was minimal in frozen flows. Pressure distributions for sharp leading edge bodies were calculated by comparing equilibrium and frozen pressure conditions, following the Prandtl-Meyer expansion method for rapid expansions. Contrastingly, gradual expansion was observed for blunt shaped bodies.
The area of the stream tube cross section was computed using the continuity equation after the density and velocity distributions were taken into account. This will reveal the location of the outermost active stream tube. The solid boundary is established by taking normal shockwaves close to the stagnation point. into consideration. Consequently, even though we took into account approximative parameters with errors, the values of the initial pressure distributions in the hypersonic flows come out precisely and the boosters that were employed. Because of the body's blunt shape, the wake region was forming behind the body and the flow was separating. Furthermore, because the hammerhead was blunt, self-excited oscillations were beginning to form.
Comparison for different shapes of warheads of a missile
By altering the fineness ratios of spherically and parabolically shaped bodies, the current study compares the distribution of shockwaves and the variation of several aerodynamic properties. We performed a computational analysis using the Spallart Allmaras model. In addition to destroying the turbulent viscosity close to the walls, this model accounts for the transportation of eddy viscosities. The measurements demonstrated that as the fineness ratio decreased, so did the separation between the detached shocks and the geometry. Furthermore, a five percent deviation from the theory of the spherically-shaped blunted nosecones was observed, according to the computational analysis results.
The shockwave is connected to the parabollically blunted nosecone; however, the spherically blunted body experiences a bow shock, which is normal to the direction of the incoming flow and becomes stagnant as it approaches the nosecone. The flow in the bow shock of a spherically blunted body must descend to coincide with the other streamlines in the flow. The expansion waves that formed at the base were responsible for this. In contrast, oblique shocks cause the flow to be parabollically blunted, which leads to the formation of expansion shocks. However, in contrast to the spherical case, expansion shocks did not form at the turning point. Reducing the fineness ratio entails increasing the nosecone's width while decreasing its length.
The heat flux was found to be greater in the vicinity of the stagnation points and then nearly constant for both bodies along the path. More so for the spherical case than the parabolic case was it observed. The cause is still unknown. In comparison to spherical bodies, parabolically blunted bodies are better suited for high fineness ratios because they produce less drag. This is stated in the concluding remarks [3].
Application of hypersonic flows
Scramjets: An examination of the scramjet was given by Nikimoni Das, et al. Working at extremely high speeds, a scramjet is a supersonic ramjet dot. Because of its high speed, the incoming air is compressed as well as arriving at very high speeds. Because of the way the scramjet is made, when air enters the inlet, it creates shock waves upon impact. Because of the shape of the scramjet inlet, the compression is accomplished by a number of shocks. Modern aerospace applications include reusable vehicles and many more that make use of the scramjet engine. It utilizes the oxygen in the atmosphere since it lacks its own supply. The air entering the scramjet is traveling at a hypersonic speed. No rotating parts are present in scramjet. A hollow scramjet tube takes the place of the compressor. Such high velocity is not possible for a scramjet to start at ground speed. Therefore, by carrying its own rocket engine for the ignition, it is most likely used in the second stage. By combining two adiabatic and two isentropic processes, the Brayton cycle serves as its basis of operation. Only a small number of nations had this technology when it was first tested by the USSR in 1991. But as for the application of this technology, even developing nations like India are keeping up.
Sukanta Roga gave a presentation on her work on the computer analysis of the scramjet injector's diamond shape. The fact that scramjets can mix fuel and take in air at high mach numbers gives them an advantage over ramjets. Inappropriate fuel-air mixing could result from this, which could have an impact on thrust production. Studies are being conducted to reduce the combustion distance and employ hydrocarbons, which have the unique property of delaying combustion in comparison to conventional fuel hydrogen, in an effort to improve this feature. For the correct mixing of fuel and incoming air separated by a flat plate parallel to the inlet, a parallel injection technique can be employed. However, this results in a change in the velocity gradients, which generates the shear layers. On the other hand, barrel shocks from an injector positioned on the wall perpendicular to the inlet mix with the boundary layer and separate the fuel both upstream and downstream. The efficiency of the combustion is impacted by pressure losses resulting from this approach.
The H2O mass fraction contours revealed that the middle of the chamber has the highest recorded mass fraction, corresponding to about half of the total mass fraction. At the end of the combustion chamber, or roughly one ninth of its length, the H2 mass fraction, as determined by the contours of H2 , was largest. Using a stoichiometric ratio of 1, the highest combustion efficiency of 88 percent was observed.
Transverse fuel injection was suggested by Jeong-Yeol Choia, et al. Research on the transverse injection of fluid in the presence of a combustion chamber cavity has been presented in this paper. To simulate the interactions in the combustion chamber, a Mentor's shear stress transport model is used. From the conventional k-epsilon model, this model was developed. It was also noticed that the Shear Stress Transport (SST) model produced better results than the others and that it was independent of the initial boundary conditions. In order to select spatial discretization techniques appropriate for the transverse velocity distribution, the MUSCL approach was employed for the computational analysis. To determine the geometry of the combustion chamber, about 1,50,000 mesh cells were used. For accurate prediction of flow interactions, the grid density was increased close to the injector and walls. For the injector hole, about 50 grid points were allocated and the minimum mesh grid element size surrounding a wall was approximately 7 × 10-7 m. Each solid wall was taken to have adiabatic properties and no slip, but the slip properties were assigned to the upper wall.
The Laurie A. computerized analysis of the scramjet has been provided by Marshall, et al. The authors of this research study discussed the necessity of modeling NASA's HYPER X-43 A scramjet. The first two flights were teste and it was discovered that the tests were very expensive. The vehicle's leading edge and the heat exchanger were corroding as a result of the intense heat. Nevertheless, the rates of likage caused by corrosion were not accurately provided by the wind tunnel tests. Consequently, they made the decision to focus on the avatars. Another reason for the simulations was that they lacked the database needed to run the HYPERX-43A scramjet, which was supposed to be used for scramjety. The vehicle's stability and aerodynamic performance would be examined using the data.
In order to fuel the scramjet, Kumari Ambe Verma, et al. used a parallel injection technique. They checked the outcomes and changed the angles of attack as well. The RANS k-w model was employed by the authors after the grid independence test, in conjunction with species transport. A non-reacting layer called shear layer is created by the wakes created by the combustion chamber's heat release. Shocks cannot mix with this layer. In one instance, authors have examined the characteristics of nonreacting flows by treating incoming gas as inert gas. The strut's angles of attack were changed from -50 to 00 to +50 in the mixing case. According to the results, even at 00 angle of attack, the 5-degree angle of attack was more efficient [4].
Concept of detonation in scramjets: An experimental and analytical investigation into the oblique shockwave in scramjet detonation was carried out by Menees, et al. On the other hand, oblique shock waves result in comparatively smaller pressure losses than normal shock waves. However, the authors were unsure if stabilized oblique shock waves existed. On the other hand, Chapman-Jouguet waves, behind which the flow has sonic velocity, are thought to be the normal shock waves. Numerous investigations have demonstrated that the scramjets' heat addition is comparable to that of oblique shock waves. In multi shock diffusers, the detonation wave may also function as the final wave. For the LEO space application, a rocket engine was taken into consideration. The mixture's temperature rises as a result of the fuel injection, but the fuel's temperature stays constant. Thus, heat loads begin to affect the scramjet material. The material absorbs about 90 percent of the heat loads. For higher mach numbers, ODE performed better than scramjet. Conversely, specific impulse declines at mach numbers below 15. This happens as a result of the oblique shock wave's increased angle. Here, the scramjet length is also very important. For ODE, shorter is better and for scramjet, longer is better. The shockwave's potential detonation-causing distance should be shortened by the experimental assembly's increased pressure behind the wedge. Premature combustion may result from raising the temperature and pressure in addition to the stagnation PR.
Types of detonation: A summary regarding the detonation engines was presented by Piotr WolaÄski. Around 1-3 km/s is the velocity produced by the detonation process. On the other hand, deflagration velocity is measured in meters per second? At that point, as temperature rises due to deflagration, pressure drops, complicating the design of adding more air to cool the turbine before it is assembled. Yet, detonation results in a low combustion temperature and high pressure. Together with a rise in specific impulse, detonation also yields a theoretical efficiency gain of the jet cycles of greater than 10%. The detonations can be broadly classified into three categories. An elongated tube loaded with an oxidizer and fuel mixture makes up the pulse detonation. Deflagration is produced during the ignition process, which subsequently transitions to detonation. Every time, the generated thrust is started and depends on the time. In order to use this kind of detonation with turbojet engines, more air must be added before the turbine. Stand-alone detonation engines are the second kind. In this kind, detonation waves are stabilized by a wedge and fuel is injected at supersonic velocity. It’s extremely constrained operating range is a drawback, however. There will be more pressure losses than thrust after Mach 7. Detonation in the toroidal combustion chamber of the rotating detonation engine is continuously propagating. Through holes in the structure, fuel is injected and oxygen is supplied. Rocket engines are able to use it.
Issues in scramjet engines: The solutions for the scramjet propulsion technology were proposed by Zonglin Jiang, et al. Shockwaves that could travel upstream and cause the turbomachinery to surge were one of the main drawbacks of the scramjet engine. That being said, the standing oblique detonation engine was suggested by the authors. Shorter combustion chamber length and higher specific impulse compared to scramjet engines are two advantages of this engine type. Rapid dissipation is possible for the sound waves created by the subsonic flow's diffusion. Experiments demonstrated that oscillating combustion, which consists of dying and rekindling flames, is caused by supersonic combustion. Three main problems primarily arise in supersonic combustion. The mach cone's mechanism is shared by the first shock wave, which is spherical in nature. A planar shock wave is created when a spherical shock wave is reflected and its effects are not as strong as those of a spherical shock wave. A negative temperature gradient in the combustor region is created by the numerous oblique shock wave reflections, which causes shock to decay later in the scramjet than in the open space. As the flow moves forward, the simulation results indicated the existence of a spherical shockwave that eventually transforms into a planar shockwave. Yet, as the flow continued, the shockwave propagation was lessened in relation to the rising mach number. A low equivalent ratio was addressed using this technique. The primary subject of this research paper is discussed.
Computational analysis
Geometry: A wedge geometry of 20 m × 20 m (base and height) was chosen for the analysis. A rectangular domain of 250 m × 150 m was chosen in which wedge was placed at 65 m from both the upper and lower fair field. On the other hand, the wedge was at a distance of 90 m from the inlet and 160 m from the outlet (Figure 1) [5].
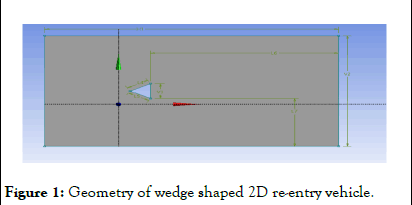
Figure 1: Geometry of wedge shaped 2D re-entry vehicle.
Meshing: Face meshing was done for the wedge with element size of 0.1 m and the overall meshing was done by taking the 0.75 m size of each element. The total number of nodes was 70355 and the total number of cells was 69548. The named selections were inlet, outlet and ff1, ff2 (Figure 2).

Figure 2: Meshing of wedge shaped 2D re-entry vehicle.
Results: The simulation was carried out by using the pressure based solving approach as the incoming flow is subsonic. The energy equation was also used for calculating the temperature. The realizable k-epsilon model was used as it was more accurate than other models. The incoming gas was chosen to be ideal gas whose density was varying along with the Sutherland law. The inlet boundary condition was set as 0.58 mach number. The residual value was set upto 10-6 . The coupled method was used along with the second order scheme for spatial discretizations like pressure, density, momentum, turbulent kinetic energy, turbulent dissipation rate and energy. A global time step method was used for the computation along with the least squares method. 1000 iterations were performed to achieve the 10-6 value of the scaled residuals for converging the solution (Figure 3-13).

Figure 3: Static pressure contour of a 2D wedge shaped re-entry vehicle at mach number 3.

Figure 4: Static temperature contour of a 2D wedge shaped re-entry vehicle for mach number 3.

Figure 5: Mach number contour of a 2D wedge shaped re-entry vehicle for mach number 3.
At mach number 5.
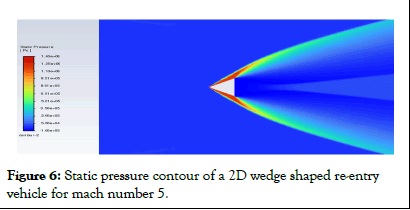
Figure 6: Static pressure contour of a 2D wedge shaped re-entry vehicle for mach number 5.

Figure 7: Static temperature contour of a 2D wedge shaped re-entry vehicle for mach number 5.

Figure 8: Mach number contour of a 2D wedge shaped re-entry vehicle for mach number 5.

Figure 9: Static pressure contour of a 2D wedge shaped re-entry vehicle for mach number 8.

Figure 10: Static temperature contour of a 2D wedge shaped reentry vehicle for mach number 8.

Figure 11: Mach number contour of a 2D wedge shaped re-entry vehicle for mach number 8.
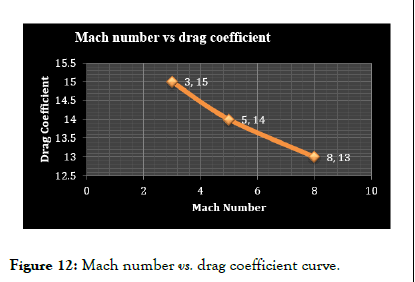
Figure 12: Mach number vs. drag coefficient curve.
Bluff body and bluff body with spike
Geometry

Figure 13: Geometry of a bluff body without spike
A bluff body of length 5 m and diameter 3 m is placed into a rectangular domain of 100 m length and 60 m height at a distance of 30 m from inlet and 27 m from bottom far field.
Meshing: The meshing was done for domain by considering the element size of 0.25 m. The inflation was done for the bluff body with the transition layer of 0.272 and the maximum layers were 7. The growth rate was 1.4 (Figure 14-37) [6].
Figure 14: Meshing of a bluff body without spike.
Figure 15: Static pressure contour of a bluff body without spike shaped re-entry vehicle for mach number 5.
Figure 16: Static temperature contour of a bluff body without spike shaped re-entry vehicle for mach number 5.
Mach number contours
Figure 17: Static temperature contour of a bluff body without spike shaped re-entry vehicle for mach number 5.
Bluff body with spike
Geometry
Figure 18: Static temperature contour of a bluff body without spike shaped re-entry vehicle for mach number.
Meshing
Figure 19: Static temperature contour of a bluff body without spike shaped re-entry vehicle for mach number 5.
Computational analysis
Figure 20: Static temperature contour of a bluff body without spike shaped re-entry vehicle for mach number 5.
Figure 21: Static temperature contour of a bluff body without spike shaped re-entry vehicle for mach number 5.
Figure 22: Static temperature contour of a bluff body without spike shaped re-entry vehicle for mach number 5.
Comparison
Figure 23: Drag coefficient curve for the comparison of bluff body with spike and bluff body without spike.
Computational analysis of hypersonic flows at different models k-epsilon
Figure 24: Static pressure contour of a 2D wedge shaped re-entry vehicle for k-epsilon model.
Figure 25: Mach number contour of a 2D wedge shaped re-entry vehicle for k-epsilon model.
Figure 26: Static temperature contour of a 2D wedge shaped reentry vehicle for k-epsilon model.
SST-k-w
Figure 27: Static pressure contour of a 2D wedge shaped re-entry vehicle for SST-K-w model.
Figure 28: Static temperature contour of a 2D wedge shaped re-entry vehicle for SST-k-w model.
Figure 29: Mach number contour of a 2D wedge shaped reentry vehicle for k-epsilon model.
Comparison of blunt body with different models
Geometry
A geometry having area equal to the edge was drawn by considering an appropriate domain.
Figure 30: Geometry of blunt shaped 2D re-entry vehicle
Meshing
The meshing was done for the blunt body by considering element size as 0.1 m and the overall meshing for domain was done by making.
Figure 31: Meshing of blunt shaped re-entry vehicle.
Spallart Allmaras model
Figure 32: Mach number contour of blunt shaped 2D re-entry vehicle for Spallart Alamaras model.
Figure 33: Static temperature contour of blunt shaped 2D re-entry vehicle for Spallart Alamaras model.
Figure 34: Static temperature contour of blunt shaped 2D re-entry vehicle for Spallart Alamaras model.
K-epsilon model
Figure 35: Static pressure contour of blunt shaped 2D re-entry vehicle for k-epsilon model.
Figure 36: Static temperature contour of blunt shaped 2D re-entry vehicle for k-epsilon model.
Figure 37: Mach number contour of blunt shaped 2D re-entry vehicle for k-epsilon model.
Observations
At mach number 5, the wedge-shaped re-entry vehicle generates two oblique shock waves at its apex, accompanied by two expansion fans at the base vertices. These shock waves cause a decrease in mach number, resulting in an increase in pressure and temperature. This change is visually represented by a transition from a higher mach number (depicted in red) to a lower mach number (depicted in lighter green). On the other hand, the expansion fans cause an increase in mach number,leading to a reduction in pressure and temperature. This transformation is illustrated by a transition from a light green shade back to red. Additionally, the presence of vortices and wake-like structures at the base of the wedge creates a region of lower mach number, represented by the color blue. Similar changes in pressure and temperature can be observed in different colors.
In the case of a blunt body, a bow shock forms at the frontal section, unlike the two oblique shocks in a wedge structure. However, all other phenomena remain consistent with the wedge configuration. For a bluff body, a bow shockwave emerges along with three smaller spherical wave fronts at the frontal extremity. In simulations involving a bluff body with a spike, an initial normal shockwave appears in front of the spike, followed by the formation of a bow shock at the forefront of the bluff body. The interaction between the normal shock and bow shock further reduces the flow velocity, resulting in a decrease in the drag coefficient. Comparative analysis shows that as the mach number increases, the drag coefficient of the wedge-shaped reentry vehicle decreases. Furthermore, a comparison between a bluff body without a spike and one with a spike indicates a decrease in drag (Figure 38-45 and Table 1) [7].
NASA X-43 a Scramjet
Geometry
Figure 38: Geometry of NASA X-43A Scramjet.
Meshing
Figure 39: Meshing of NASA X-43A Scramjet.
| Boundary name | Boundary condition type | Boundary condition value |
| Inlet | Velocity inlet | Mach no 5, Gaugage pressure 0, Temperature 300 k, Turbulent intensity 10% |
| Far field | Wall | Wall conditions |
| Outlet | Pressure outlet | Outlet guage pressure 0, Temperature 300 K, Turbulence intensity 10% |
Table 1: Boundary conditions for NASA x-43 a scramjet.
At 0 degrees angle of attack
Figure 40: Static temperature contour of NASA X-43A Scramjet at mach 5 and 0 degrees angle of attack.
Figure 41: Mach Number contour of NASA X-43A Scramjet at mach 5 and 0 degrees angle of attack.
At 5 degrees AOA
Figure 42: Static temperature contour of NASA X-43A Scramjet at mach 5 and 5 degrees angle of attack.
Figure 43: Mach number contour of NASA X-43A Scramjet at mach 5 and 5 degrees angle of attack.
Figure 44: Mach number contour of NASA X-43A Scramjet at mach 5 and 10 degrees angle of attack.
Figure 45: Static temperature contour of NASA X-43A Scramjet at mach 5 and 10 degrees angle of attack.
Observations
An external geometry of NASA X-43A hyper scramjet vehicle was simulated at mach 5 and different angles of attack 0, 5 and 10. All major parts of external geometry of scramjet were producing the shocks including inlet leading edge, engine intake, rudder and elevator.
The leading edge was producing oblique shock which was weak. The shock interaction was happening in between rudder and elevator shocks. A region of high temperature was produced starting from the tail section.
The static temperature contours showed that the temperature was maximum around the scramjet and it decreased as the distance from the scramjet was decreased. This was shown by the red coloured layer followed by a light green coloured layer around the scramjet. One light green coloured layer starting from the engine intake went downwards with the diminishing intensity. This was due to the shock occurred due to the nozzle inlet shape which increased the pressure of incoming flow. Similar phenomenon was occurred for the shock produced around the rudder. The mach number contours also showed the shocks occurred due to the engine inlet and rudder. In addition to this, it also showed a weak oblique shockwave at the tip of the scramjet vehicle. But, after angle of attack 10 degrees it diminished. The yellow coloured region in the mach number contour at 10 degress shows the formation of region similar to the stagnation region having lower velocity. It also showed that the nozzle inlet and the rudder shocks were nullified. As the angle of attack was increased, the thickness of the red layer around the vehicle increased, which showed the increase of heat. This also represents increase in drag. Also the temperature distribution from the 10 degrees angle of attack was changed to concentric circles for each zone (Table 2 and Figures 45,46) [8].
Simulations on internal geometry of scramjet
Geometry
|
Scramjet section |
Area |
|
Inlet nozzle |
0.4095 m2 |
|
Throat |
0.2426 m2 |
|
Outlet of isolator |
0.2426 m2 |
|
Oultet of 1st section of combustion chamber |
0.3397 m2 |
|
Outlet of 2nd section of combustion chamber |
0.67 m2 |
|
Exhaust |
0.9 m2 |
Table 2: Dimensions of internal scramjet geometry.
Figure 45: Geometry of internal scramjet geometry of NASA X-43 A.
Meshing
Figure 46: Meshing of internal scramjet geometry of NASA X-43 A.
Pre-processing
A simple approach was followed for the computational analysis of the scramjet. First a density based approach was selected by selecting the energy equation along with double temperature model. The k-epsilon realizable turbulence model was selected for the analysis. The incoming air was chosen to be an ideal gas and viscosity was kept tpo vary with Sutherland’s law. The boundary conditions were chosen according to the below mentioned table. Spatial discretization methods were chosen to be implicit, along with the AUSM Scheme. All other schemes were chosen to be third order MUSCL. The residuals were set to be 10-6 and the solution was initialized standardly from inlet (Table 3 and Figures 48-61).
| Boundary name | Type | Conditions |
| Inlet | Pressure far field | Mach=5,7.5,10 P=0 Pa T=300K |
| Far field | Wall | Wall conditions |
| Fuel injector | Pressure far field | M=1,2,3 P=0 Pa T=300K |
| Outlet | PRESSURE outlet | M=0.6 P=0 Pa T=300K |
Table 3: Boundary conditions of internal scramjet geometry of NASA X-43 A.
Figure 48: Mach number contour of internal scramjet geometry of NASA X-43 A.
Figure 49: Static temperature contour of internal scramjet geometry of NASA X-43 A.
Figure 50: Static pressure contour of internal scramjet geometry of NASA X-43 A.
Figure 51: Static temperature contour of internal scramjet geometry of NASA X-43 A at mach 7.5.
Figure 52: Static pressure contour of internal scramjet geometry of NASA X-43 A at mach 7.5.
Figure 53: Mach number contour of internal scramjet geometry of NASA X-43 A at mach 7.5.
Figure 54: Static pressure contour of internal scramjet geometry of NASA X-43 A at mach 10.
Figure 55: Static temperature contour of internal scramjet geometry of NASA X-43.
Figure 56: Static pressure contour of internal scramjet geometry of NASA X-43 A at mach 7.5 and 5 deg AOA.
Figure 57: Static temperature contour of internal scramjet geometry of NASA X-43 A at mach 7.5.
Figure 58: Mach number contour of internal scramjet geometry of NASA X-43 A at mach 7.5 and 5 deg AOA.
Figure 59: Static temperature contour of internal scramjet geometry of NASA X-43 A at AOA10 deg and mach 7.5.
Figure 60: Static pressure contour of internal scramjet geometry of NASA X-43 A at AOA 10 and mach 7.5.
Figure 61: Mach number contour of internal scramjet geometry of NASA X-43.
Observation
When air came inside the combustion chamber through the inlet of a scramjet engine, it produced oblique shocks due to striking on the aerospike shaped fuel injectors. These shocks then reduced the speed of the incoming flow and due to the shock and boundary layer interaction the fuel was mixed with the incoming air effectively. As the mach number was increased the number of reflections of the shocks of incoming air were reduced. This was because the increased mach number causes increase in the speed of the incoming air which causes less time of air to have interaction with fuel in the combustion chamber.
Hence, the efficiency of mixing of fuel with the air decreases. The static temperature contours showed that the temperatures of the flames were increased after the mixing of fuel with the air due to the shockwave boundary layer interaction. The mach number of the fuel was lesser as compared to the incoming air. As the flow goes ahead, the mach number increased due to the mixing of fuel with air but, it decreased at the regions were shockwave interacted with the flame. At the last, the intensity of shocks was diminished and the mach number of the flame was increased. As the angle of attack of the injection of fuel was increased, the fuel was mixed with the air more efficiently along with the decrease in speed and increased pressure regions were formed. With the increasing angle of attack, the flame was spread more in the combustion chamber. Increasing mach number also increases the thickness of thermal boundary layer along with increased temperature of flame (Figures 62,63) [9].
Detonation
Geometry
Figure 62: Geometry of internal scramjet with a single wedge shaped fuel injector.
Figure 63: Meshing of internal scramjet with a single wedge shaped fuel injector.
Pre-processing
A simple approach was followed for the computational analysis of the scramjet. First a density based approach was selected by selecting the energy equation along with double temperature model. The k-epsilon realizable turbulence model was selected for the analysis. The incoming air was chosen to be an ideal gas and viscosity was kept tpo vary with Sutherland’s law. The boundary conditions were chosen according to the below mentioned table. Spatial discretization methods were chosen to be implicit, along with the AUSM Scheme. All other schemes were chosen to be third order MUSCL. The residuals were set to be 10 ^ -6 and the solution was initialized standardly from inlet (Tables 4,5 and Figures 64-79).
|
Boundary name |
Type |
Conditions |
|
Inlet |
Pressure far field |
Mach=5,7.5,10 |
|
Far field |
Wall |
Wall conditions |
|
Fuel injector |
Pressure far field |
M=1,2,3 |
|
Outlet |
Pressure outlet |
M=0.6 |
Table 4: Boundary conditions of internal modified scramjet geometry of NASA X-43 A hyper scramjet.
| O2 | 0.232 |
| N2 | 0.736 |
| H2O | 0.032 |
| H2 | 0 |
Table 5: Species mole fraction for inlet air.
Figure 64: Static pressure contour of internal scramjet at Mach 5.
Figure 65: Static temperature contour of internal scramjet at Mach 5.
Figure 66: Velocity contour of internal scramjet at Mach 5.
Figure 67: Mach no contour of internal scramjet at Mach 10.
Figure 68: Static pressure contour of internal scramjet at Mach 10.
Figure 69: Static temperature contour of internal scramjet at Mach 10.
Variation of fuel
Figure 70: Static pressure contour of internal scramjet when used ethanol as fuel at Mach 10.
Figure 71: Mach no contour of internal scramjet when used ethanol as a fuel at Mach 10.
Figure 72: Velocity magnitude contour when ethanol is used a fuel at Mach 10.
Variation of angle of attack
Figure 73: Mach no contour of internal scramjet when ethanol is used at Mach 10 and AOA 5.
Figure 74: Static temperature contour of internal scramjet engine.
Figure 75: Velocity contour at Mach 10 and AOA 5.
Figure 76: Velocity contour at mach 10 and 5 degrees angle of attack.
Figure 77: Temperature contour of internal scramjet at Mach 10 and AOA 10.
Figure 78: Velocity contour of internal scramjet at Mach 10 and AOA 10.
Figure 79: Pressure contour of internal scramjet at MACH 10 at AOA 10.
Observations
A detonation wave preceding the isolator segment exhibited a velocity lower than that of the flow within the isolator segment, thereby serving to avert the occurrence of an upstream shockwave and the consequent unstart of the engine. The stability of detonation waves was assessed subsequent to the computational scrutiny of a scramjet featuring a solitary fuel injector. The simulations entailed the alteration of the mach numbers to 5 and 10, alongside the substitution of hydrogen with diverse fuel ethanol. Furthermore, the assessment of stability involved the variation of angles of attack up to 5 and 10 degrees [10].
Upon reaching an Angle of Attack (AOA) of 10 degrees, it was observed that the pressure attained its peak subsequent to the flow impacting the fuel injector wall. The pressure then commences a decline as the flow transitions in an upward trajectory, coinciding with the maximum temperature post the formation of a shockwave at the wall's surface.
With an escalation in the mach number, a reduction in the thickness of the detonation wave was noted. Additionally, the utilization of ethanol as a fuel source led to the observation of an asymmetrical detonation wave, characterized by the presence of two minor bow shocks. Moreover, an increase in the angle of attack resulted in an upward inclination of the detonation wave.
Modeling hypersonic flows and their practical implications have revealed several key findings:
The increase in mach number was found to correspond to an escalation in the drag experienced by re-entry vehicles. Moreover, the configuration of these vehicles played a crucial role in determining the nature of shock waves surrounding them. Specifically, wedge-shaped re-entry vehicles were associated with oblique shocks at their apex, while blunt-shaped ones exhibited bow shocks. In addition, it was observed that a bluff body featuring a spike generated less drag compared to a spikeless counterpart.
The verification of the external geometry of the NASA X-43 A hyper scramjet vehicle facilitated an in-depth exploration of external flow patterns around the craft. Furthermore, it was noted that the efficiency of fuel mixing within the combustion chamber of the internal scramjet varied inversely with Mach number but directly with the angle of attack.
Computational analysis focusing on the stability of detonation waves highlighted that alterations in fuel composition led to changes in the shape of the detonation wave. Additionally, modifications in the bow structure of the detonation wave were observed, with a tendency for it to lean more towards an upward orientation.
[Crossref]
Citation: Surwase P (2025) Modelling of Hypersonic Flows and their Applications. J Aeronaut Aerospace Eng. 14:376.
Received: 06-Jun-2024, Manuscript No. jaae-24-31908; Editor assigned: 11-Jun-2024, Pre QC No. jaae-24-31908 (PQ); Reviewed: 25-Jun-2024, QC No. jaae-24-31908; Revised: 21-May-2025, Manuscript No. jaae-24-31908 (R); Published: 28-May-2025 , DOI: 10.35841/2168-9792.25.14.376
Copyright: © 2025 Surwase P. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.