Journal of Antivirals & Antiretrovirals
Open Access
ISSN: 1948-5964
ISSN: 1948-5964
Research Article - (2015) Volume 7, Issue 2
Among people infected with HIV, liver related complications have become the second leading causes of morbidity and mortality. A mathematical model is developed and analysed to investigate the ability of different combinational therapy to inhibit viral production in liver cells. Therapy efficacy in form of dose-response function is incorporated. Analysis of the model suggests that it is possible to reduce the effective reproductive number below unity provided that therapy efficacy is more than 90%. Simulation results show that combinational therapy of didanosine, lamivudine, atazanavir and nelfinavir is the most effective while zidovudine, stavudine, atazanavir and nelfinavir is the least effective in terms of inhibiting viral production. The findings suggest that mathematical models can be employed to recognize which of the current treatment protocols perform best in controlling HIV replication in the liver.
<Keywords: HIV inhibition, Hepatocytes cells, CD4+ cells, Antiretroviral therapy
Infectious diseases are the second leading cause of death among humans worldwide and the number one cause of death in developing countries [1]. Among all other previous pandemic like cholera and influenza, the human immunodeficiency virus (HIV) has for three decades socially and economically affected the world and has claimed over 25 million lives [2].
Among people infected with HIV, liver disease has become the second leading cause of morbidity and mortality [3]. Various researches reveal that liver disease can occur solely due to HIV infection [4-7].
During HIV infection, the virus uses envelope glycoprotein 120 (gp120) to access entry into the host cell by binding on the CD4 receptor or a coreceptor on the host cell. The most common coreceptors for HIV are C-X-C chemokine receptor type 4 (CXCR4) and C-X-C chemokine receptor type 5 (CXCR5) [8-11]. Recent studies show that in addition to CD4+ cells, HIV can infect other cells provided they possess either of the coreceptors [8].
Human hepatocytes possess CXCR4 making them susceptible to HIV invasion and hence causing hepatocyte apoptosis by viral signaling through CXCR4 [12]. A study by Kong et al. [13] indicates that although there has been a number of contradictions regarding HIV replication in hepatocytes [11,12], the cells support the first and last stages of HIV production. However, Kong et al. [13], reveals that replication in hepatocytes is low compared to viral replication in CD4+ cells. In addition to hepatocytes, HIV productively infects other hepatic cells and macrophages, especially, kupffer cells [14,15].
Since the introduction of antiretroviral therapy (ART) scientists have aimed at getting the drug that can limit HIV replication and hence reduce the viral load in the body. To date, no drug with 100% efficacy and ability to eradicate the virus from within HIV infected bodies has been found.
Mathematical models have been used to study within-host dynamics of HIV. Gumel et al. [16] uses a heaviside function to investigate the effects of intermittent IL-2 plus ART on the dynamics of HIV, after using therapy for 200 days. The findings show that in spite of the combined effect of the theoretical maximum, anti-HIV cytotoxic Tlymphocytes (CTLs) action and 100% efficacies of therapy coupled with IL-2 therapy, the virus continues to persist.
Rong et al. [17] includes a combination of reverse transcriptase inhibitors (RTIs) and protease inhibitors (PIs) in a mathematical model of HIV infection with two strains of HIV. They assess the progression rate of exposed CD4+ cells (eclipse phase) back to uninfected stage and viral production on the evolution of drugresistant virus. They further investigate the evolution of drug resistant strains in the presence of antiretroviral treatment and the range of drug efficacies under which drug-resistant strain will be able to invade and out-compete the wild-type strain. Results show that when the drug efficacy is not high enough to exert sufficient selective pressure (RTI efficacy of 0.5 and PI efficacy of 0.3), the resistant strain is unable to invade the established sensitive strain.
Arnaout et al. [18] uses a basic within host model, as by Perelson and Nelson [19], to analyse HIV dynamics in vivo. They incorporate treatment as drug effectiveness parameter between 0 and 1 to assess the dynamics of infection below and above the threshold efficacy. Results from model analysis show that if effectiveness is below a certain threshold (1%), viral load may bounce back after a transient reduction. They further deduce that if effectiveness is below but sufficiently near the threshold, viral load may still be reduced to quite low level.
Liver disease in HIV infected people who are not co-infected with viral hepatitis, is linked to use of ART [7], because of the toxic nature of all classes of ART. However, recent studies, [4,6,7] show that HIV infection and replication in the liver cells can cause liver disease in HIV mono-infection prior to initiation of ART. Despite their unwanted effects, antiretroviral drugs have improved the long term outlook of HIV infected patients. A number of within-host mathematical models of HIV dynamics are focusing on viral progression in CD4+ cells [16-18]. Since there is evidence that HIV infect other cells, we study the progression of HIV in hepatocytes when antiretroviral therapy is administered.
This study therefore intends to use a mathematical model coupled with numerical simulations to study the ability of individual drugs as well as recommended therapy combinations, to inhibit viral replication in liver cells. Unlike most studies, [16,20-22], this study considers drug efficacy as a dose-response function as recommended by Perelson and Deeks [23].
In the model formulation, we define the eight variables as follows: uninfected CD4+ (Tc), exposed CD4+ cells (Ec), infectious CD4+ cells (Ic), uninfected hepatocytes (Th), latently infected and not activated hepatocytes (If) as by [24], productively infected hepatocytes (Ia), HIVspecific cytotoxic T-lymphocytes (L) and viral load (V).
Model parameters are as follows: CD4+ cells and hepatocytes are produced from within the body at rates λ1 and λ2, and die naturally at rates b1 and b3, respectively. At infection, the virus infects target hepatocytes with probability q at rate β2 and target CD4+ cell with probability (1-q) at rate β1 [17-20]. Propose that when HIV enters a resting CD4+ cell, the RNA may not be completely reverse transcribed into DNA and the unintegrated virus may decay before reverse transcription. This results in a proportion of exposed cells reverting to the uninfected state at a rate α. If reverse transcription takes place, however, the cell becomes infectious at a rate π. This implies that if reverse transcription takes place in a period 1/α, where 1/α<1/π, then the exposed cell reverts to uninfected state; otherwise, it will proceed to the infectious state. Infected CD4+ cells die at rate b2 where b2>b1 and are cleared by HIV-specific CTLs at a rate k1.
When a hepatocyte is exposed to the virus, there is a probability p that it becomes productively infected (viral replication takes place after successful reverse transcription) and probability (1-p) that the cell becomes latently infected, such that there is no viral production until cell activation (the extent of stimulation of cellular processes initiated as a response to external stimuli reaching the cell). Latently infected hepatocytes are activated to become productively infected at rate μ. Decay rates for productive hepatocytes and latently infected hepatocytes are b4 and b3, respectively, where b4>b3 as shown in a study [21-24]. It is assumed that latently infected hepatocytes and healthy hepatocytes decay at the same rate (b3). Productively infected 4 hepatocytes are killed by HIV-specific CTLs at rate k1 and, until activated, latently infected hepatocytes will not trigger the action of CTLs. Based on a study [20], this study assumes that latently infected hepatocytes will either get activated to become infectious or die. Thus there is no possibility of them becoming uninfected again.
With or without any pathogen in the body, CTLs proliferate naturally at rate x and in the presence of HIV infection they proliferate at rate k2 proportional to the number of infectious cells. The CTLs are cleared at rate b5. HIV is produced by infectious CD4+ and productively infected hepatocytes at average rates s1 and s2 per cell, respectively. In addition to CD4+ and hepatocytes, research by [14,15,25], argue that HIV productively infects other cells and macrophages, like Kupffer cells in the liver. These cells produce virions at rate m. Virions die naturally at rate b6.
There are three types of antiretroviral drugs currently used as therapy for HIV. Non-nucleoside reverse transcriptase inhibitors (NNRTI), nucleoside reverse transcriptase inhibitors (NRTI) and protease inhibitors (PI). NNRTIs prevent the enzyme (reverse transcriptase) from converting RNA of HIV to DNA, so that HIV does not multiply. NRTI latches onto the new strand of DNA that reverse transcriptase tries to build. PIs prevent final assembly and completion of new HIV viruses within the cell, resulting in the infected cells producing non-infectious virus. However, this study considers only infectious virus.
Mathematical models such as [16,20-22] include therapy efficacy as a number between 0 and 1. There are however, a number of underlying dynamics especially the pharmacokinetics of the medication that influence the drug efficacy. For example, in a recent study by Perelson and Deeks [23], the importance of determining a dose that gives 50% of the maximum response, as a way of quantifying the potency of the drug, is highly emphasized. This finding follows an earlier research by Shen et al. [26] who uses a Hill equation to describe the effectiveness of HIV medication. Perelson and Deeks [23] hence recommend that it would be of great contribution if the efficacy of ART would be modeled as a dose-response function.
Shen et al. [26] explain the importance of the dose-response curves in terms of predicting which medication works perfectly in inhibiting viral replication. They find that PIs have higher gradients implying better efficacies, leading to a conclusion that, this is the reason why PIs are very effective in treating HIV.
However, in a typical dose-response relationship, response to a dose depends on a number of factors including the dose administered, the frequency of dosing as well as the pharmacokinetics of the particular drug. In this study, we assume that dose and rate of dosing lead to a "steady state" dose response, that is, after administering a particular dose repeatedly, the drug concentration reaches a steady state. We therefore assume a steady effective therapeutic exposure to the drug because with infections such as HIV, "steady state" pharmacokinetics as opposed to initial or loading doses is more reliable for the effects of the treatment.
This study further assumes sufficient exposure to the drug (no under dosing or poor exposure due to use of substandard drugs), thus ruling out the possibility of partial suppression, which would lead to selection pressure. The model also considers early stages of treatment where the infection is presumed to be sensitive to the drugs, thus, leading to negligible drug resistance.
Taking φ1 as the therapeutic response of reverse transcriptase inhibitors and φ2 as the therapeutic response of protease inhibitors, where 0 ≤ φ1, φ2 ≤ 1, the therapeutic response function is taken to be a Hill equation (2.1) that describes the effectiveness of the drug and is given by
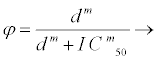 (2.1)
(2.1)
where φ=φ1 or φ2, d is variable drug dose concentration, IC50 is drug concentration that leads to 50% of the maximal viral inhibition and m is gradient of the dose-response curve corresponding to individual drugs. The response in this case is the drug efficacy or ability to inhibit viral replication [26]. The gradients of the dose-response curves of HIV drugs are given by [27]. φ1 describes the ability of a drug to stop the new strand of HIV DNA that the enzyme reverse transcriptase is trying to make from the ribonucleic acid (RNA). φ2 on the other hand is the ability of the drug to prevent the final assembly and completion of new HIV viruses within the cell.
This study assumes that reverse transcription in CD4+ cells does not occur immediately at infection, as suggested by Rong et al. [17]. So reverse transcriptase inhibitors (RTIs) reduce the rate of transfer of cells from exposed to infectious class (π). In hepatocytes, it is the infection rate that gets reduced by RTIs, because it is assumed that at infection, reverse transcription takes place after which the cell becomes latent or productive. It is for this reason that a cell cannot become uninfected again like in the case of CD4+ cells.
If protease inhibitors are 100% effective, no latently infected cell becomes productive. The study therefore assumes that PIs reduces the rate of activation from latent to infectious (μ). It is further assumed that the effect of medication is translated generally into minimal viral load. Thus, viral productions from macrophages are also inhibited by both RTIs and PIs. The combined responses of PIs and RTIs in macrophages are therefore (1−φ1)(1−φ2), as stated in [24].
From the assumptions and description above we got the following system of ordinary differential equations (2.2)-(2.9).
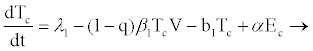 (2.2)
(2.2)
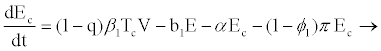 (2.3)
(2.3)
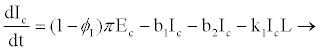 (2.4)
(2.4)
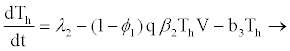 (2.5)
(2.5)
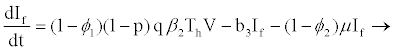 (2.6)
(2.6)
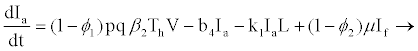 (2.7)
(2.7)
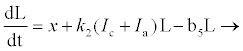 (2.8)
(2.8)
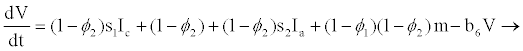 (2.9)
(2.9)
The system of equations (2.2)-(2.9) settles to a disease-free equilibrium point
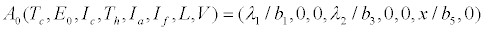
The effective reproduction number for the system (2.2)-(2.9), calculated using the next generation method as in [28] is
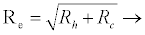 (3.1)
(3.1)
Where
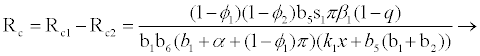 (3.2)
(3.2)
for
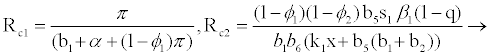 (3.3)
(3.3)
and
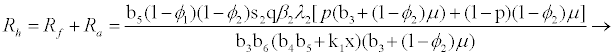 (3.4)
(3.4)
for
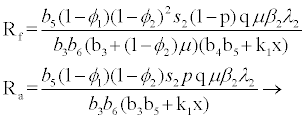 (3.5)
(3.5)
Rf and Ra are the number of secondary infections from latently and productively infected hepatocytes respectively. Rc1 and Rc2 are the number of secondary infections produced by cells in the eclipse phase (latent) and virus producing CD4+ cells respectively. Rc and Rh is the number of secondary infections produced by one virus in CD4+ and hepatocyte, respectively. Re is the total number of secondary infections in the liver. The total number of secondary infections is directly proportional to the clearance rate of CTLs and inversely proportional to the clearance rate of virions. Secondary infections in either type of cells largely depend on the drug efficacy. It can be seen that if the drug is 100% effective (φ1=φ2=1), then there is no secondary infections in either cell type.
Generally, the number of secondary infections (Re) is dependent on antigen-independent CTLs proliferation rate (x) and independent of antigen-dependent proliferation rate (k2). This indicates that if the CTLs are boosted prior to infection, then the body can handle infection better than when they proliferate in the presence of infection.
We study the behaviour of the effective reproduction number for specific model parameter values as presented in Table 1. When p=0, then with the activation rate μ =0.019 and 50% efficacy of both PIs and RTIs and all other parameters as shown in Table 1, numerical simulations show that the effective reproductive number of hepatocytes can be reduced below unity, as shown in Figure 1.
| Par | Description | Value | Source |
|---|---|---|---|
| λ1 | rate of creation of CD4+ from within the body | 10(ml)−1 | [21] |
| b1 | natural death rate of uninfected CD4+ | 0.01 | [20] |
| q | probability that HIV infects hepatocytes | 0.2 | Estimate |
| p | probability that at infection, hepatocyte becomes productively infected | 0.3 | Estimate |
| µ | rate at which latently infected hepatocytes become productive | 0.006 | Estimate |
| β1 | rate of transmission of HIV in CD4+ | 0.00015(ml)−1 | [21] |
| x | antigen-independent CTLs proliferation rate | 20 | [16] |
| k2 | antigen-dependent proliferation rate of CTLs | 0.2 | [24] |
| α | rate at which exposed CD4+ become uninfected | 0.01 | [17] |
| π | rate at which exposed CD4+ become infectious | 0.23 | [17] |
| b2 | death rate of infected CD4+ due to infection | 0.5 | [29] |
| k1 | rate at which CTLs kill infected CD4+ and hepatocytes | 0.4 | Estimate |
| λ2 | rate of creation of hepatocytes from within the body | 100(ml)−1 | Estimate |
| b3 | natural death rate of hepatocytes | 0.002 | [30] |
| β2 | rate of transmission of HIV in hepatocytes | 0.000015(ml)−1 | Estimate |
| b4 | death rate of hepatocytes due to infection | 0.05 | Estimate |
| b5 | rate of clearance of CTLS by all means | 0.15 | [18] |
| s1 | average rate of production of virions by an infected CD4+ | 50,000 | [31] |
| s2 | average rate of production of virions by an infected hepatocyte | 1000 | Estimate |
| b6 | death rate of HIV | 2 | [29] |
| m | rate of production of virions from macroghages | 5 | [16] |
Table 1: Parameters values as used in the model of HIV infection in the liver while therapy is administered.
However, if the probability p=1, that is, every exposed cell becomes infectious at infection, then the number of secondary infections is greater than unity. It can also be seen that to keep Rh below unity, p should be less than 0.4093. Thus, it can be considered important to increase drug efficacy as well as reduce activation rate of latently infected hepatocytes in order to reduce the effective reproductive number below unity. Figure 1 shows that with only 30% of hepatocytes becoming productive at infection, the threshold activation rate below which the hepatocytes effective reproductive number can be below unity is 0.0096.
Analysing the combined dependence of the effective reproductive number on p and μ at the same time, it is noted from the right panel of Figure 2 that, there are multiple parameter value combinations for p and μ at which the effective reproductive number is unity. That is, with the probability of a hepatocyte becoming productive at infection less than 0.6, the corresponding activation rate μ lower than 0.019, therapy efficacy of 50% and all other parameters as stated in Table 1, HIV infection in hepatocytes can possibly be managed.
Considering CD4+ cells, with the rate of transfer of exposed to infectious stage π=0.23 and assuming therapy efficacy of 50%, the effective reproductive number is below unity when the probability p is above 0.9266, as noted in Figure 3. Thus, it can be possible to manage HIV infection in CD4+ cells given the parameter values listed in Table 1 and if almost all HIV were to infect only hepatocytes. However, it is stated in [13] that HIV has higher affinity for CD4+ cells than hepatocytes. We therefore assume a probability of 0.8 that HIV infects a CD4+ as shown in the right panel of Figure 3. The effective reproductive number is seen to be below unity given that the rate of transfer from exposed to infectious CD4+ cells is below 0.019. The range of values of q and π that give the effective reproductive number below unity were as shown in Figure 4.
In all the previous simulations, the therapy efficacy has been fixed at 50% for both drug classes. However, medically it is not the case that all classes of ART are 50% effective. We therefore investigate the drug efficacy that would lead to an effective reproductive number less than unity. Figure 6 shows that, given μ=0.0096, p=0.4093, q=0.9266 and π=0.019, it is possible to have Re<1 provided the therapy efficacies are greater than 90%.
Figure 5: Effective reproduction number Re (left panel) and its corresponding level lines (right panel). The number is calculated with varying drug infection rates β1 and β2, with values of p, μ, q and π as optimized with respect to Rh=1 and Rc=1, and with all the other parameters as given in Table 1.
Figure 6: Effective reproduction number Re (left panel) and its corresponding level lines (right panel). The number is calculated with varying drug efficacies Φ1 and Φ2, with values of p, μ, q, π and m as optimized with respect to Rh=1 and Rc=1, and with all the other parameters as given in Table 1.
In Figure 5 we show the dependence of the effective reproduction number Re on the infection rates β1 and β2. Apparently, the infection might not proceed to endemic state if drug efficacies are fixed at 50% given the infection rates β1<0.0015 and β2<0.00015 for CD4+ cells and hepatocytes, respectively.
In this section we present numerical simulations of model equations (2.2)-(2.9). Parameter values for the model are all shown in Tables 1-4. Some parameters are from literature where as some are estimated. The estimates include; probability that HIV infects hepatocytes, probability that at infection, hepatocyte becomes productively infected, rate at which latently infected hepatocytes become productive, rate of transmission of HIV in hepatocytes, death rate of hepatocytes due to infection, average rate of production of virions by an infected hepatocyte. Parameter values for all these rates are assumed lower than the corresponding values of CD4+ cells. This is because Kong et al. explain that much as HIV infects and replicates in hepatocytes, but the affinity as well as the level of viral production is low in these cells as compared to CD4+ cells. On the other hand, rate of creation of hepatocytes from within the body was estimated to be higher than that of CD4+ cells because we assumed that inside the liver, hepatocytes are more dominant than CD4+ cells.
| Medication | d [μM] | m | IC50 [nM] |
|---|---|---|---|
| Zidovudine (AZT) | 37.41 | 0.1452 | 29.40 |
| Didanosine (DDI) | 28.22 | 0.1774 | 28.93 |
| Lamivudine (3TC) | 5.00 | 0.1935 | 4.80 |
| Stavudine (d4T) | 1.00 | 0.1855 | 89.09 |
Table 2: Parameter values of NRTIs medication used in therapy efficacy equation.
| Medication | d [µM] | m | EC50 [nM] |
|---|---|---|---|
| Efavirenz (EFV) | 3.17 | 0.2742 | 0.87 |
Table 3: Parameter values of NNRTIs medication used in therapy efficacy equation.
| Medication | d [μM] | m | EC50 [nM] |
|---|---|---|---|
| Atazanavir (ATV) | 7.09 | 0.4354 | 2.19 |
| Nelfinavir (NFV) | 62.76 | 0.2903 | 26.90 |
Table 4: Parameter values of PIs medication used in therapy efficacy equation.
Figure 7 shows the general dynamics of HIV infection prior to initiation of therapy. The viral load (V) grows steeply in the first days, leading to increased number of latently infected CD4+ (Ec), productively infected CD4+ (Ic), latently infected hepatocytes (If) and productively infected hepatocytes (Ia). This results in a clear drop in the numbers of uninfected CD4+ (Tc) and hepatocytes (Th) cells. That significant decrease takes place within the first day of infection and it can be seen that most of those previously uninfected cells start to contribute to all the classes of infected cells. Following the progression of the infection, there is a significant response of HIV-specific CTLs to infection at a rate k2, as shown in equation (2.8). That helps the liver to reduce the viral population but cannot eliminate it completely. As we have seen in the Re analysis in Figure 6, the number of secondary infections will always be greater than unity when the drug efficacies are zero (φ1=φ2=0). The graphs show that without any medical intervention the infection is destructive to the liver.
Analysing the model with therapeutic effect of the drugs (equations (2.2)-(2.9)), the study considers medication as listed in Tables 2-4. The sample drugs under study are representatives of all classes of ART commonly used as medication for HIV, namely, NRTIs, NNRTIs and PIs. Tables 2-4 present all the parameters which are used to calculate drug efficacy as shown in equation (2.1). All doses are expressed as concentrations in moles per liter.
Antiretroviral treatments are always used in combinations of three or four drugs from specific classes. However, we first simulate the infection dynamics when each drug is administered individually with its usual dose. The goal is to verify how every individual drug is able to inhibit viral production and hence reduce the viral load. Figure 8 depicts the dynamics. The first immediate observation is that the infection level reduces when either drug is used. However, the severity of the influence varies significantly from one medicine to another. Apparently, a drug that reduces the number of infected CD4+ most effectively does not perform equally well in hepatocytes. The most distinct aspects of infection dynamics are the time delay before the infection peaks and the maximum level reached by the infection.
In particular, the study considers the detailed Figure 9 for the viral load when individual drugs are used. If drug efficacy is measured by reduction in viral population, then atazanavir is clearly the best performing drug. Of all medications considered in this study, ATV is clearly the treatment which is capable of delaying and dampening the peak of infection.
Considering 2007 World Health Organisation recommendations of using ART, that is, two NRTI and one NNRTI drug (2NRTI+1NNRTI) or two NRTI and two PI drugs (2NRTI+2PI), the study presents simulation results when the aforementioned combinations are considered. Out of the drugs used in the study, as shown in Tables 2-4, we obtained six different pairs of NRTI drugs combined with a single NNRTI drug or with the two PI drugs. Figure 10 shows the infection dynamics for the 2NRTI+1NNRTI combinations.
Combinations have higher efficacy than each single drug on its own. The number of uninfected cells remains at higher levels when combinations are used as compared to single drug. Consequently, the number of infected cells and viral populations are reduced more with combinations than with single drugs. In most of the cell types it is visible that the best combination in all aspects is DDI+3TC+EFV, whereas the worst one is AZT+d4T+EFV.
We then consider the drug combinations of 2NRTI+2PI. As presented in Figure 11, these options are even more efficient in infection reduction. This is consistent with the previous simulations of individual drugs that reveal how ATV is the best in viral reduction among the considered drugs. When combined with another PI drug and two more drugs from NRTI class, ATV proves to be the strongest of all treatments studied in this work. Simulation results show that DDI+3TC+ATV+NFV is the best combination and AZT+d4T+ATV +NFV is the worst one.
The aim of this study was to find the most and least effective drug combination that inhibits viral production in liver cells during HIV monoinfection. HIV infection and replication in CD4+ cells, hepatocytes and macrophages were considered. In CD4+ cells, reverse transcription was considered not to occur immediately at infection. The same consideration is taken for hepatocytes, though unlike CD4+ cells that can return to uninfected state, hepatocytes could only die or proceeds to infectious state after being exposed to the virus. HIV therapy included the three classes of enzyme inhibitors, namely, NRTIs, NNRTIs and PIs. Drug efficacy was considered as a doseresponse function with parameters obtained from pharmacological studies of [26,27].
Analysis of the model’s effective reproduction number showed that the key parameters to control the infection are: p-the probability that at infection, a hepatocyte becomes productively infected, q-the probability that HIV infects hepatocyte and not CD4+, μ-the rate at which latently infected hepatocytes become productive, and π-the rate at which exposed CD4+ become infectious. In particular, considering all the other parameters as shown in Table 1 and fixing each drug efficacy at 50%, it was shown that in order to possibly keep the number of secondary infections below unity, the crucial parameters need to satisfy the conditions, p<0.4093, q>0.9266, μ<0.0096 and π<0.019. This means that if more hepatocytes become latent than productive at infection, then the infection would be controlled. This reduces the viral population in the liver since there is a possibility that the virus would die while within the cell before the final viral assembly [17].
The effective reproduction number was found to be below unity only when the infection rates for CD4+ cells and hepatocytes were respectively β1<0.0015 and β2<0.00015, whereas these values are sometimes suggested as high as 0.005 [21]. With all parameters fixed at their theoretical values in Table 1, it was seen that strict control of the infection may be possible when the drug efficacy of either type of enzyme inhibitor exceeds 90%. This is, however, in contradiction with a study by Gumel et al. [16] who found that even if HIV drugs are 100% effective, the infection would still persist in CD4 cells.
Simulation results further suggest that ATV is possibly the best single drug and 4dT the worst in terms of viral load reduction. This was consistent with literature that protease inhibitors are more effective than reverse transcriptase inhibitors in terms of viral load reduction in HIV infection [26-31]. Among the considered full ART combinations, with effectiveness measured in terms of reducing the viral load as well as the number of infectious hepatocytes, DDI, 3TC, ATV and NFV was the best option and AZT, d4T, ATV and NFV was the worst. Since the PIs used are the same, we can therefore say that the difference in antiviral activity is due to the NRTIs used. 3TC and DDI that are known to have a good antiviral activity are recommended to be used as initial therapy for HIV as compared to 3TC, AZT or 3TC, d4T [32]. On the other hand it has been recommended that AZT should not be combined with d4T because the combination does not lead to increase in CD4+ cells after initiation, and that it actually perform worse than d4T alone due to pharmacological antagonism [33]. We have shown that PIs are more effective than NNRTIs in terms of viral load reduction. In either PI-based or NNRTI-based regimen, with parameter values as shown in Table 1, DDI combined with 3TC seem to be the most effective first line HIV medication while d4T combined with AZT have the least antiviral activity.