Journal of Physical Chemistry & Biophysics
Open Access

Methane Second Virial Coefficient Analysis

Yilkal Dessie^{* *}Correspondence: Yilkal Dessie, Department of Applied Natural Science, Adama Science and Technology University, P.O. Box: 1888, Adama, Oromia, Ethiopia, Email:

Author info »

Abstract

The virial coefficients provide valuable information on the intermolecular forces of a particle. Thus measurement of the second virial coefficients for Methane is described. The result of second virial coefficient for Lennard Jones is tabulated over a wide range of temperature. At low temperatures (T ≤ 300 (K), the virial coefficients B (T) is negative, where the attractive part of the interaction potential so that there is a good agreement between experimental and calculated results. There is a large discrepancy at higher temperatures (T˃300 (K), the second virial coefficients B (T) is positive, and where the repulsive part of the interaction potential for molecule is dominates. For Methane, from the calculated second virial coefficient, we obtain the Boyle’s temperature, . At this temperature methane molecule is considered as an ideal molecule.

Introduction

The virial coefficients provide valuable information on the intermolecular forces of a particle. Using different type of potential, the virial coefficients for several materials have been calculated over a wide range of temperature [1-3]. The behavior of a substance in its gaseous or liquid state tends to be dominated by the fact that the molecules within it exert forces upon one another. We do, of course, have the concept of a perfect gas, for which PV=RT, an equation which results when all intermolecular forces are set to zero, but real substances only approximate to this in the gaseous state at low pressures. At higher pressures, generally above a few bars, the influence of the intermolecular forces becomes increasingly important until at about 100 bars pressure they may even dominate [4,5]. This conditions cause the intermolecular forces become different from zero i.e., the molecule is highly affected by interaction either by an attraction or repulsion with an equation of a state given by [6,7].

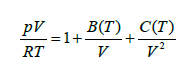
Where V, p, and T are the molar volume, pressure, and absolute temperature while R is gas constant. The temperature dependent quantities B (T) are known as C (T) the second and third virial coefficients, respectively. Lennard-Jones showed in another remarkable work showed that for intermolecular potentials written as binomials of arbitrary powers of the intermolecular distance, the corresponding second virial coefficient B (T) can be calculated exactly as an infinite power series. The intermolecular potential between the molecules of the real gas is the Lennard-Jones potential. So, the second method consists in finding the inversion temperature Ti evaluating dB/dT=0 numerically. Hence, the temperature at which B (T)=0 is called the Boyle temperature [8].

The brief description of intermolecular potentials would be understood from the energy of interaction, U, of two molecules at a separation, R, with the function rewrite as, U(R). Then the energy dependent second virial coefficients is

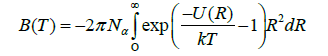
Where N_a Avogadro’s number and k is is Boltzmann’s constant. A fair Approximation to U(R) for many molecules is given by the Lennard-Jones potential:

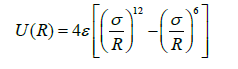
This is strongly repulsive (positive) at small R and weakly attractive (negative) at large R. the potential contains only two parameters; σ and ε. σ is called the collision diameter of the molecule. It is equal to the separation at which U(R)=0. ε is the depth of the potential well at the point at which is a minimum.

Reasonable values for σ methane can be obtained from the size of the molecule 3.8 Å. But information on ε is more difficult to obtain. Thus one reasonable way to obtain this result is to compare calculated value for B (T) with experimental one [9].

The purpose of this work is to prepare theoretical estimation values of effective temperature dependent potential, second virial coefficient for Methane (CH₄) which helps to obtain the Boyle’s temperature. This is used to calculate the temperaturedependence of second virial coefficient for Methane which compares the work with the experimental results.

Experimental

For evaluating the second viral coefficient and Boyle temperature ‘’VIRIAL’’ program was applicable at a given and known values of σ and ε/k.

Results and Discussion

From the plot of root mean square value (Δ) versus ε/k is perfectly an upward parabolic curve shown from Figure 1. This parabola has a minimum value so that from this graph by using the equation given and using mathematical laws the first derivative of the function (i.e., dy/dx=0), results x=ε/k=177.26 (at this value the respective y coordinate=RMS (root mean square value)=Δ=error=6.39). R-squared (regression coefficient) value R2=0.975, this indicates that the constructed curve would be acceptable and relate the parameter between Δ and ε/k (i.e., the failure between them is week). The minimum value of the parabola indicates an optimum value for ε/k. There for, analyzing such a parameter once help to understand deviations become minimum between calculated and experimental values of second virial coefficient B(T).

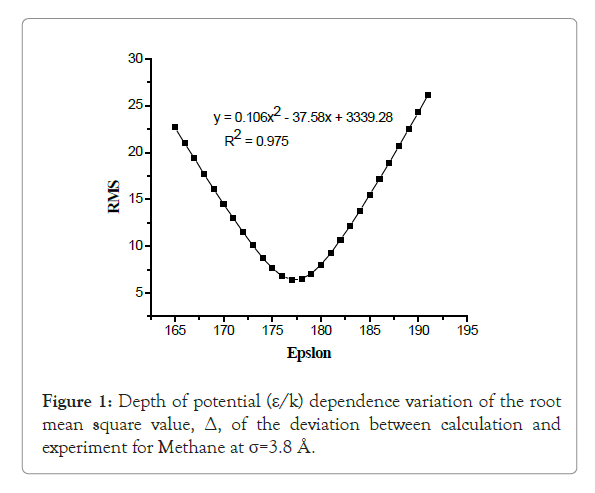
Figure 1: Depth of potential (ε/k) dependence variation of the root mean square value, Δ, of the deviation between calculation and experiment for Methane at σ=3.8 Å.

The variation of second viral coefficients B (T) with temperature is shown in Table 1 and Figure 2. From the table and graph the calculated values of B(T) over the given temperature range coincide closely with the experimental values. This relation indicates the parameter ε/k is a good estimation of that which describes the molecule. Second virial coefficient, B (T) shows qualitative agreement with experimental values.

Table 1: Comparison of calculated and experimental values of B (T) with temperature in (K) at ε /k=177.26 (K) and σ=3.8 Å.

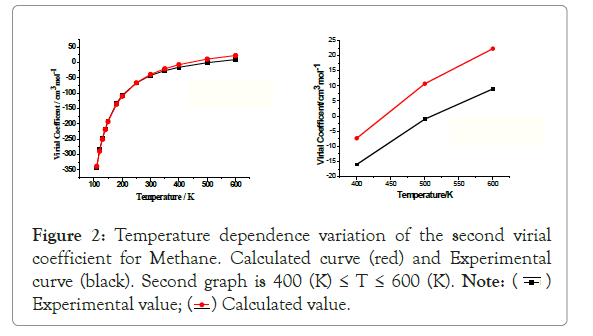
Figure 2: Temperature dependence variation of the second virial coefficient for Methane. Calculated curve (red) and Experimental curve (black). Second graph is 400 (K) ≤ T ≤ 600 (K).

From experimental data on the second virial coefficient of B (T) methane shown from Figure 2 is the best fit of Lennard- Jones parameters [1]. At low temperatures (T ≤ 300 (K), the virial coefficients B (T) is negative, where the attractive part of the interaction potential so that there is a good agreement between experimental and calculated results. There is a large discrepancy at higher temperatures (T˃300 (K), the second virial coefficients B (T) is positive, and where the repulsive part of the interaction potential for molecule is dominates shown in Figure 2. The temperature at which B (T) tends to zero is called the Boyle’s Temperature TB [1]. For Methane, from the calculated second virial coefficient, we obtain the Boyle’s temperature, . At this temperature methane molecule is considered as an ideal molecule (i.e., neither attraction nor repulsion is dominated) [6].

Conclusion

The virial coefficients provide valuable information on the intermolecular forces of a particle. Thus measurement of the second virial coefficients for Methane is described. The result of second virial coefficient for Lennard Jones is tabulated over a wide range of temperature. At low temperatures (T ≤ 300 (K), the virial coefficients B (T) is negative, where the attractive part of the interaction potential so that there is a good agreement between experimental and calculated results. There is a large discrepancy at higher temperatures (T˃300 (K), the second virial coefficients B (T) is positive, and where the repulsive part of the interaction potential for molecule is dominates.

Acknowledgements

The Author greatly thanks to applied chemistry program, Adama Science and Technology University, for financing.

References

1. Kumar R, Tomar R. Numerical evaluation of second virial coefficient and boyle’s temperature for argon. Int J Appl Sci Technol. 2014;5:1-4.

   [Google Scholar]

2. De Rocco AG, Halford JO. Intermolecular potentials of argon, methane, and ethane. J Chem Phys. 1958; 28(6):1152-1154.

   [Crossref] [Google Scholar]

3. Harvey AH, Lemmon EW. Correlation for the second virial coefficient of water. J Phys Chem Ref Data. 2004; 33(1):369-376.

   [Crossref] [Google Scholar]

4. Shokouhi M, Parsafar GA. A new equation of state derived by the statistical mechanical perturbation theory. Fluid Ph Equilibria. 2008;264(2):1.

   [Crossref] [Google Scholar]

5. Tulegenov AS, Wheatley RJ, Hodges MP, Harvey AH. Intermolecular potential and second virial coefficient of the water-nitrogen complex. J Chem Phys. 2007;126(9):094305.

   [Crossref] [Google Scholar] [PubMed]

6. Korfali O. The second and third density virial coefficients of six Ar-Ne mixtures at 25.0° C. Turk J Chem. 2002;26(5):641-652.

   [Google Scholar]

7. Koga K. Osmotic second virial coefficient of methane in water. J Phys Chem. 2013;117(41):12619-12624.

   [Crossref] [Google Scholar] [PubMed]

8. Wisniak J. On the boyle temperature. Indian J Chem Technol.1994;1:261-265.
9. Atkins P, De Paula J. Physical chemistry for the life sciences. Oxford University Press. 2011.

   [Google Scholar]