Journal of Drug Metabolism & Toxicology
Open Access
ISSN: 2157-7609
ISSN: 2157-7609
Research Article - (2016) Volume 7, Issue 2
Keywords: Methotrexate; Psoriasis; Oral administration; Mathematical model
MTX: Methotrexate; 7OH-MTX: 7-Hydroxymethotrexate; C7OHMTX( s) : The Laplace Transform of a Mathematical Function Approximating the Plasma Concentration-Time Profile of 7- Hydroxymethotrexate of the Patient; CMTX(s) : The Laplace Transform of a Mathematical Function Approximating the Plasma Concentration-Time Profile of Methotrexate of the Patient; s: The Complex Laplace Variable; H : The Dynamic System; H(s) : The Transfers Function
The study [1] described the early phase (3 months) of therapy of psoriatic patients with MTX. Besides that, it described an investigation of pharmacokinetics and pharmacodynamics of methotrexate (MTX) and 7-hydroxymethotrexate (7OH-MTX), the major metabolite of MTX [1-9]. In the initial pilot study [2], coauthored by the author of this study, an advanced mathematical modeling method was developed and used to create combined mathematical models for MTX and 7OHMTX using the data obtained from the authors of the study [1]. The current study provided a further example of a successful use of an advanced mathematical modeling in pharmacokinetics [2,10-15]. The method considered here was exemplified by the mathematical modeling of the formation of 7OH-MTX from MTX in patients treated for psoriasis with MTX over the time period of 3 months.
In the study [1], MTX was administered to psoriatic patients in an oral dose of 15 mg once per week. In an initial pilot study [2], coauthored by the author of the current study, an advanced modeling method was developed and successfully used to model the formation of 7OH-MTX from MTX. The current study is a sequel to the previous studies [1,2], therefore, combined mathematical models for MTX and 7OH-MTX were developed.
The mathematical modeling started with the definition of a patientspecific dynamic system, denoted by H , in the complex domain [2,10-15]. The patient-specific dynamic system H was defined in such a way that the Laplace transform of a mathematical function approximating the plasma concentration-time profile of MTX of a patient (see Figure 1) was used as the mathematically relevant input of MTX to the patient’s body and/or to the dynamic system H and the Laplace transform of a mathematical function approximating the plasma concentration-time profile of 7OH-MTX of a subject (see Figure 2) was used as the mathematically relevant output of the dynamic system defined. After that, the dynamic system defined was described with the transfer function (denoted by H(s) ) in the complex domain:
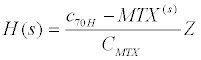 (1)
(1)
In Eq. (1), C7OH-MTX(s) is the Laplace transform of a mathematical function approximating the plasma concentration-time profile of 7OH-MTX of the patient, CMTX(s) is the Laplace transform of a mathematical function approximating the plasma concentrationtime profile of MTX of the patient, and s is the complex Laplace variable. In the following text, the patient-specific dynamic systems were simply called the dynamic systems H .
A mathematical model of a dynamic system defined was developed using the advanced mathematical modeling method described in the studies published previously [2,10-15]. The mathematical models developed were used to determine: plasma metabolic ratios of MTX, rates of the formation of 7OH-MTX from MTX, and mean formation time of 7OH-MTX from MTX.
Patient No.1 was randomly selected among all patients enrolled in the study [1] and in the current study, to show an example of the results obtained. Figure 1 shows observed plasma concentration-time profile of MTX.
Figure 2 shows observed plasma concentration-time profile of 7OHMTX and the description of the observed profile with the developed model of the dynamic system defined.
Figure 3a, 3b, and 3c shows the rate of the formation of 7OH-MTX from MTX in the first, the second and third phase of treatment, respectively.
As seen, the rate of the formation of 7OH-MTX from MTX decreased from the maximum value of about 0.52±0.09 l/h in the first phase of treatment to the maximum value of about 0.29±0.07 l/h in the third phase of treatment, respectively.
The determined quantities: metabolic ratios of MTX to 7OH-MTX, mean time of the formation of 7OH-MTX from MTX are listed in Table 1.
| The first phase of treatment | The second phase of treatment | The third phase of treatment | |
|---|---|---|---|
| Metabolic ratio | 0.67 ± 0.08* | 0.58 ± 0.05 | 0.59 ± 0.09 |
| Mean formation time of 7OH-MTX from MTX (h) | 9.35 ± 1.79 | 9.90 ± 1.02 | 15.59 ± 2.22 |
| *SD; MTX: Methotrexate; 7OH-MTX: 7-hydroxymethotrexate. | |||
Table 1: Shows metabolic ratios of MTX to 7OH-MTX, mean time of the formation of 7OH-MTX from MTX and rates of the formation of 7OHMTX from MTX.
It can be observed that metabolic ratios remained approximately constant during the first three phases of treatment.
However, the mean time of the formation of 7OH-MTX from MTX increased from the value of about 9.35 ± 1.78 h in first phase of treatment to value of about 15.9 ± 2.22 h in the third phase of treatment. The mean formation time of 7OH-MTX from MTX increased from the value of about 9.35 ± 1.79 h, in the first phase of treatment to the value of about 15.59 ± 2.22 h in the third phase of treatment. Analogous results hold for all patients enrolled in the study [1] and in the current study.
The dynamic systems used in the current study were mathematical objects, without physiological significance.
They were merely working tools, used: 1) to mathematically represent static and dynamic properties of the formation of 7OH-MTX from MTX [16-18] in all patients enrolled in the study published previously [1], and in the current study; 2) to describe how one state of the formation process of 7OH-MTX from MTX developed into another state of the formation process over the time course of treatment [16-18]; 3) to mathematically represent dynamic processes associated with methotrexate metabolism in all psoriatic patients.
The mathematical modeling method used in the current study has been described in detail in the previous studies authored and/or coauthored10 by the author of the current study [2,-15].
Transfer functions, used in the current study, are fundamental equations of the theory of dynamic systems. They are not unknown in pharmacokinetics [19,20], where transfer functions are usually called disposition functions [21-23].
Even though the metabolic pathways of MTX have been well elucidated and several studies [3-9], little is known about time dependent changes in the formation of 7OH-MTX from MTX in patients undergoing treatment for psoriasis with MTX.
Therefore, computational investigation of time dependent changes in the formation of 7OH-MTX from MTX in patients undergoing treatment for psoriasis with MTX was performed in the current study.
On purpose, mathematical details of the method used were not included. Instead, readers interested in the mathematical details of the method used were referred to literature.
The models developed in the current study did not attempt to address all aspects of the formation process of 7OH-MTX from MTX in patients treated for psoriasis, because no mathematical model can exactly describe such a complicated process as is a metabolic formation proces. Therefore, further investigations in humans are required to identify un-modeled aspects of the formation of 7OH-MTX from MTX in the current study.
The theory of dynamic systems is a well-established theory which deals with analyses of dynamic systems. Disadvantages of modeling methods that use tools from the theory of dynamic systems are as follows: these methods seems to be quite computationally complex, equations used are formulated in terms of Laplace transforms in the complex domain, what gives rise to different problems, some of them being unexpected. The methods considered here require an appropriate theoretical framework; see for example full text articles, available free of charge at: http://www.uef.sav.sk/durisova.htm. However, the use of tools from the dynamic systems for modeling purposes offers the following advantages: no specific model structures are necessary, no abstract unrealistic assumptions of homogenous wellmixed body parts (in general unrealistic) are not necessary.
Computational and modeling tools from the theory of dynamic systems are not commonly used in pharmacokinetics. However, these tools can be employed advantageously in pharmacokinetic studies, as exemplified in the previous studies [10-15] and in the current study. More information about successful use of computational and modeling tools from the theory of dynamic system in pharmacokinetics can be found in several full-text articles which are available free of charge at the author’s web page (an English version): http://www.uef.sav.sk/ advanced.htm.
Much work remains to be done for further development of the modeling method used in the current study, and the implementation of the modeling method used in user-friendly modeling software. Clinical significance of the results obtained in the current study with respect to the use of MTX in the treatment of different cancers must be verified by additional investigations. For this reason a full utilization of the results obtained lies far in the future.
The modeling method employed in the current study can be used to model any drug metabolized in the body; under the condition that drug disposition in the body is at least approximately linear and parent and metabolite blood concentration-time profiles are available.
The current study reaffirmed that an integration of key concepts from pharmacokinetics and bioengineering is a good and efficient way to study dynamic processes in pharmacokinetics, because such integration combines mathematical rigor with biological insight.
The author gratefully acknowledges the financial support from the Slovak Academy of Sciences in Bratislava, Slovak Republic. The author also thanks the authors of the study Chládek et al. who provided the data used in the current study.
No potential conflicts of interest relevant to this article.