ADS: Advanced Design System; DMA: Dodecahedron Microstrip Antenna; FIS: Fuzzy Interference System; NUSS: New Ultra Small Satellite; MAN: Microstrip Antenna Network

Ultra-Small Universities researches, that allows researchers to participate and contribute in USS [1,2] development and use various satellite technology and participate in several original scientific experimental implementations that results researches opting to test new technologies before they are explored in space. In this context, we study the development of a 3D structure with dodecahed microstrip antenna [3] network modeling for new USS development. Proposed new architecture permits a full visibility of USS with corresponds station [4]. New USS technologies appeared ten years ago, and hundreds of copies have already been in orbit. The Femto Satellite is a USS weighing less than one hundred grams and operating with some mW of Electric power consumption [5]. Accurate standard was established, called N–Prize, which defined the constraints of Femto Satellite in order to classify the USS and determine its mission in Leo [6]. The work proposes a solution for maximizing USS visibility with corresponding station, we develop a new Dodecahed Microstrip Antenna network. To synthesize a total visibility USS radio transmission access solution capable of meeting the ever-increasing demands for improvements inter station/ Femto Satellite disconnection rates. Proposed architecture uses antenna element of the Dodecahed MA as a fundamental component of this overall system solution.

Proposed dodecahedron architecture for femto satellite

In geometry, a dodecahedron is any polyhedron with twelve flat faces. Dodeca is a prefix meaning "twelve". But usually a regular dodecahedron is meant: a Platonic solid. It is composed of 12 regular pentagonal faces, with three meeting at each vertex. It has 20 vertices, 30 edges as well. Its dual polyhedron is the Icosahedron. The dodecahedron, described by Buckminster Fuller as 6 pentagonal spheres, is a polyhedron of which is composed entirely of regular pentagons. We have done this mathematical analysis inorder to build this polyhedron.

Studied mathematical dodecahedron volume

In order to determine the volume of the dodecahedron, we will use the pyramid method. There are 12 pentagonal pyramids, one for each face, each pyramid beginning at O. The volume of any n-sided pyramid is 1/3 * area of base * pyramid height (Figure 1).

Figure 1: Pentagon is the area of the 5 triangles.

First, we need to get the area of the base, which is the area of each pentagonal face, and the area of the pentagon is the area of the 5 triangles which compose it.

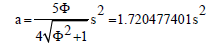
** The height of the pyramid, OU

To do that, we need to find the distance from O to a vertex, let’s say, OH. This distance will be the hypotenuse of the right triangle OUH. Since we already know UH, we can then get OU from the Pythagorean Theorem. Imagine a sphere surrounding the dodecahedron and touching all of its vertices. OH is just the radius of the enclosing sphere. If you look at Figure 2, HOZ=GON=Diameter. There is a line through HOZ to show the diameter.

Figure 2: Rectangle MIFK.

Now, if we look at the rectangle MIFK. The diagonal of it, MF, is also a diameter (MF=HZ). Notice that the long sides of the rectangle, MK, and IF, are diagonals of the two large pentagons ADMQK and FEIRP. We know that the diagonal of a pentagon is Φ* side of pentagon.

We also can see from Figure 2 that the sides of the large pentagons themselves are diagonals of the pentagonal faces of the dodecahedron DA is a diagonal of the face ABCDE). That means each side of the large pentagons is Φ * s and that MK (any of the diagonals of a large pentagon) is Φ* Φ * s.

So MK=Φ ² s.

In fact, the dodecahedron is composed of rectangles divided in Extreme and Mean Ratio. In the icosahedron, we found these rectangles to Φ rectangles.

In the dodecahedron, they are Φ rectangles.

In rectangle MKIF, MK=IF=Φ² s, MI=KF=s, as shown in Figure 3.

Figure 3: MK=IF=Φ² s, MI=KF=s shown in rectangle MKIF.

There are 30 sides to the dodecahedron, and therefore 15 different Φ² rectangles. All of this as explanation of finding the distance OH from Figure 1, and because, we do not use a trigonometry, we need OH in order to get the pyramid height, OU in Figure 2. Notice that MHFZ is also a Φ ² rectangle and that HZ is the diagonal of it. We find HZ, then OH is just 1/2 of that.

Diameter² = HZ²= MZ²+ HM²=Φ 4 +1= (3 Φ+2) +1= 3 Φ +3 = 3 Φ²

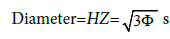
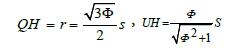
Now, we find OU, the height of the pyramid (Figure 4). From area of pentagon, we know the distance mid-face to any vertex of a pentagon. So,

Figure 4: Dodecahedron central angle.

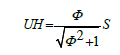
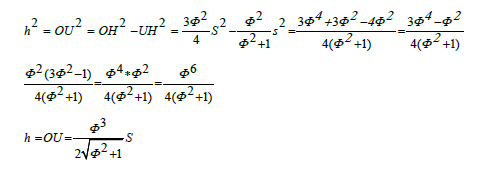
The volume of 1 pyramid =1/3 * area base * pyramid height

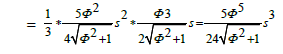
The volume of dodecahedron =12 * the volume of 1 pyramid=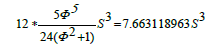

Or,

The volume of dodecahedron

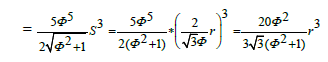
Note that (from Figure 1)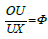

Mathematically, it is equals to:

The surface area of the dodecahedron =12

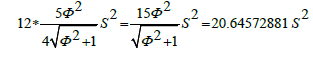
Or,

The surface area of the dodecahedron =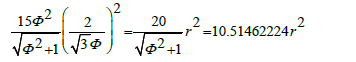

Let’s determine the central angle of the proposed dodecahedron, for example angle HOC

HC=side of dodecahedron, so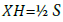

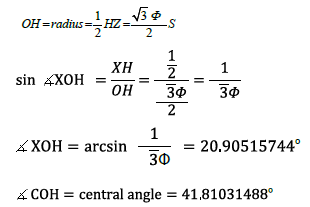
Since each face of the dodecahedron is a pentagon, the surface angle=180°. For evaluation of distance from the centroid to any midedge, while we're at it, as in Figure 4, let’s get OX, the distance from the centroid to any mid- edge.

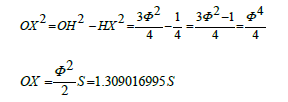
The dihedral angle is AXH. AH is one of the long sides of any of the 15 Φ² rectangles which compose the dodecahedron. AX and HX are the height h of the pentagon.

We know from the characteristic of the pentagon that the height h of the pentagon is:

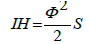
We know from Figure 3 that AH is Φ² s,

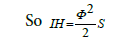
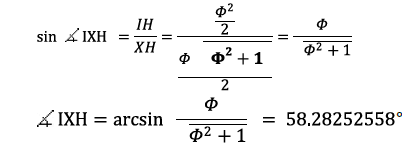
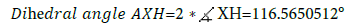so, to summarize, we obtained:

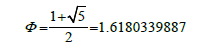
Now let us look in more detail of a fuzzy controller for the antenna network. The input of the controller is the dozen signal (signal_1, signal_2…signal_12). It is admitted that the controller named its inputs at moment of receiving the signals. So, the first signal received is taken as signal_1, the second as signal_2 and so on. The output or decision of the controller is a constant result (sugeno) representing the decision between the 12 antenna existed. The linguistic labels are modelled as fuzzy subsets of signal_1, signal_2…signal_12 (Figures 5 and 6).

Figure 5: Dodecahedron dihedral angle study.

Figure 6: Fuzzy logic models.

The Particular choice of membership functions chosen to represent the linguistic labels is not arbitrary. One of the adjustments made during testing of the control system will be experimenting with different membership functions, that is, changing the parameters of these triangular functions The FIS Editor displays as Figure 7 general information about a fuzzy inference system. There is a simple diagram at the top that shows the names of each input variable on the left, and those of each output variable on the right. The sample membership functions shown in the boxes are just icons and do not depict the actual shapes of the membership functions. Used FIS Structure as Figure 5 is the MatLab object that contains all the fuzzy inference system information. This structure is stored inside each GUI tool.

Figure 7: Upper part of FIS editor.

Access functions such as getfisand setfis make it easy to examine this structure. All the information for a given Fuzzy Interference System is contained in the FIS structure, including variable names, membership function definitions, etc. Successful simulation result on Microstrip Antenna element, resonance frequency equals 2.8 Ghz (S band) as presented in Figures 8 and 9.

Figure 8: Structure of fuzzy inference system.

Figure 9: Antenna element of dodecahedron MA model simulation results.

The Dodecahedron Microstrip Antenna (DMA) developed model is mainly studied to ensure the need of full visibility in 360 degrees. By mathematical modelling, we obtained a spherical antenna network form the element is studied by ADS tools, and successful results are obtained. We can externally control the resonance frequency by varying the tensor permeability which is a function of the magnetization of used materials for the Dodecahedron antenna network.

The Authors would like to acknowledge the financial support of this work by grants from General Direction of Scientific Research (DGRST), Tunisia, under the ARUB program. We acknowledge also the Professor Elya B. Joffs for his contribution towards the present article.