Journal of Oceanography and Marine Research
Open Access
ISSN: 2572-3103
ISSN: 2572-3103
Review Article - (2014) Volume 2, Issue 1
Two papers published before the Apollo landings showed that the ring spacing of a plurality of multi-ringed lunar maria precisely fit the pattern for explosion-generated gravity waves in a “liquid” overlying a rigid substrate, if frozen at times related to their respective explosion energies. Liquidity was attributed to transient melting of an initially hot, plastic layer beneath a rubble crust, owing to pressure relief behind the shock fronts from energetic meteoroid impacts, and freezing to subsequent solidification, upon restoration of isostatic pressure. This interpretation was largely ignored; most geophysicists thought the moon too rigid to sustain gravity waves. Here I show that current acceptance of an initially molten proto-moon with a thin crust credibly supports the “tsunami-like” generation of the lunar maria and provides new insight to the moon’s thermal history.
<Keywords: Lunar tsunamis, Moon, Lunar maria
For nearly forty years lunar scientists have searched in vain for some formulation giving the unique ring spacing of the multi-ringed maria [1]. Yet, all this time, the long sought formulation was published as a single line in a 1968 paper [2]. In that paper it has been shown that the theory for explosion–generated water waves provided a perfect fit to the five mountain rings of the lunar Mare Orientale (Figure 1), subject to the constraint that the waves propagated over a 50 km rigid substrate, and solidified abruptly after an hour. In a second paper [3], it has been demonstrated that the same formulations fit the rings of some sixteen other maria, suggesting that a 50 km mantle layer overlying a denser substrate was a universal property of the early moon. This layer is now recognized as the lunar Moho [4]. Following the Apollo landings, my papers remained virtually unnoticed. Lacking any credible alternative, I now show that: (1) an updated theoretical model for explosion-generated water waves applies beyond coincidence to the impact-generated ring structures of six principal maria, both in amplitude and phase; and (2) recent acceptance of a molten proto moon [5], supported by an existing model of the moon’s early thermal structure [6] and its behavior under impact stress [7], can be interpreted as providing the transient fluidity necessary to produce the maria as they exist today.
Figure 1: Near vertical photograph of Mare Orientale, showing close agreement between all five computed (white) and observed mountain rings. Ring 3 (Rook Mountains) rises 3 km above the equilibrium lunar surface. All rings show collinear traces of ejecta from the (invisible) crater, and the valleys between them show post facto evidence of subsurface lava venting.
Relevant theory is reviewed here for lack of important details omitted from the original papers [2,3]. The 1968 interpretation of the tsunami-like character of multi-ring Maria resulted from a 1950’s investigation of the wave making potential of large thermonuclear devices being tested in the Marshall Islands [8]. That investigation prompted a concurrent extension of the Cauchy-Poisson wave problem [9] to impulsive sources of finite size in water of finite depth [10], which only required calibration by large chemical explosions [11] to establish a scaling factor between explosive vis-à-vis water wave energy.
In a cylindrical coordinate system with the origin at the surface of a liquid of depth h, the displacement from equilibrium η following the gravitational collapse of a parabolic crater of radius ro and depth d is given for any radial distance r and time t by [11]:
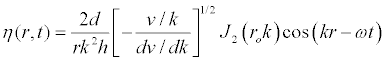 (1)
(1)
where, k = 2π/λ is the wave number, λ = wavelength, ω = wave frequency, v = group velocity, and g = gravity. Group velocity and frequency are related to wave number by the auxiliary equations:
ω2 = gk tanh kh (a); and v = (ω/2k) (1 + 2kh/sinh 2kh) (b). (2a,b)
In equation (1), the factorable cosine term gives the positions of the wave phases (crests or troughs) in the r,t plane; for example, wave crests will occur whenever
kr – ωt = π(2n – 1), n = 1, 2, (3)
where, n is the crest order number, reckoned from the point n = 0 when r = t √ gh, which marks the (invisible) wave front in r,t space.
Equation (3) is the long sought formula giving the positions of the mare rings at any time t or distance r from the center (r = t = 0) of the arbitrary disturbance that produced them.
Figure 2 shows the (invisible) Wave front, moving at constant speed r = t√gh, and the trajectories of the first six wave crests (1 - 6) calculated from Equation (3), radiating from the origin and curving upward to the right. The six vertical dashed lines connect points denoting the observed radii of rings of the six major lunar maria listed in Table 1. The fact that, with few exceptions, the crest trajectories also intersect the same points is perhaps the best evidence of their tsunamilike origin. The vertical dashed lines are, in fact, particular solutions of Equation (3), obtained graphically by plotting the observed crest radii for each mare vertically on a separate sheet of paper, and then sliding it along the time axis of Figure 2, so as to obtain the best fit to all the crest trajectories. The resulting intersections of these lines with the time axis were also interpreted as the “freezing time” (t = to) for each mare listed in Table 1.
| Mare | impactor radii (km) | Crater radii (km) | Ring radii (km) | Freezing time (min) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||||
| Imbrium | A | 11.4 | 81 | 1125 | 850 | 580 | 495 | 275 | 86 |
| Serenitatis | B | 9.7 | 71 | 900 | 650 | 460 | 310 | 205 | 75 |
| Crisium | C | 8.9 | 68 | 750 | 540 | 370 | 270 | 175 | 69 |
| Nectaris | D | 7 | 57 | 660 | 430 | 310 | 200 | 120 | 59 |
| Humorum | E | 6.2 | 51 | 600 | 400 | 212 | 170 | 105 | 55 |
| Orientale | na | 9,1 | 68 | 680 | 465 | 310 | 240 | 180 | 62 |
Table 1: Comparative impactor, crater, and mountain ring radii (km) for Orientale and five front side maria, assuming common impactor-target density, and 12 km sec–1 impact velocity. Ring data are from Reference [12]. Highest amplitude crests are shown in boldface.
Wave theory, of course, has no freezing time for wave crests. Freezing is here attributed to prompt solidification of the transient magma layer in which the waves were formed and propagated (see Lunar mare formation).
The intersections of the heavy dashed line labeled Basin locus with the wave crest curves give the locus in r,t space of the highest wave in the system, denoted by any vertical line; ergo, the first maximum of the Bessel function J2 (rok) which modulates the wave amplitudes in Equation (1), (see dashed curve bounding wave crests in Figure 3c). Thus the diamond point in each of the six mare lines lying closest to the Basin locus denotes the wave of greatest amplitude. The equation of the Basin locus is: r = 0.39 t √gh.
Figure 3: Conceptualization of the generation of the Orientale wave system. The fluidity necessary for crater collapse into the high spike leading to wave formation is presumed to arise from impact (Bingham) conversion of hot rock into viscous magma. Freezing of the wave system, and local mantle uplift to form a mascon, are presumed to result from degradation of shear-strain in the wave system resulting in recrystallization of the magma.
As with Orientale, these basins are much larger than the impact craters that produced their respective ring systems. Their crater radii, ro (Table 1), are also determined from the above Bessel function, whose argument has a maximum, (rok = 3.0) at the mare freezing time, t = to. For Orientale, the appropriate wave number k, is determined by eliminating the wave frequency ω between Equations (2a) and (3) and solving for the maximum ring radius (n = 2):
k r2 - to (gk tanh kh)1/2 = 3π (4)
where, bold characters indicate evaluation at to = 62 min. (3720 sec), r2 = 465 km, g = 1.62 m/sec, and h = 50 km = constant for all maria [3]. The solution for k is simplified by defining the dimensionless wave number σ ≡ kh and iterating to find σ = 2.20. Substituting k = σ/h into the above Bessel argument yields ro = 3.0 h/σ = 68.2 km for the Orientale impact crater radius.
The amplitude η of the highest ring, however, cannot be estimated without some specification of the transient, crater depth d. Adopting the generic, scalable relation, d ≈ ro, developed by O’Keefe and Ahrens [13] for hypervelocity impacts into zero strength, like-density targets, and taking [(v/k)/(dv/dk)]1/2 = 2.2, [6], Equation (1) becomes:
η = 2 dh [(v/k)/(dv/dk)]1/2 J2(rok)/r σ = 3.3 km , (5)
which is surprisingly close to the maximum Orientale crest height (3.0 km) reported to me from shadow lengths [2].
Figure 3 shows a simulated conjecture of the impact-generation of Orientale, in which an 18.6 km diameter sphere, traveling at 12 km/sec, penetrates the moon’s zero strength crust and hot substrate to a depth of 68 km (3a). Crater Ejecta is assumed to be distributed quite evenly to an observable radius of about 700 km. Assuming impact-induced fluidization of the hot crustal substrate, the 136 km transient crater forms within 2.4 min and collapses within 10 min to a molten lava spike 70 km high (3b). Crater collapse is accompanied by a permanent massive uplift (mascon) of about 40 km in the mantle beneath [14]. Like a pebble dropped into a shallow pond, a series of five circular waves radiate outward. Wave amplitudes are governed by the Bessel function, J2(rok) shown by the dashed wave envelope (3c) at time t = to = 62 min, when freezing occurs.
Corresponding data for five front side lunar maria, calculated in the same manner, are included in Table 1. Figure 4 shows them grouped together in what I shall call the “Imbrium Cluster” (IC). They are distinguished from Orientale, which lies on the moon’s southwest limb, by massive post-forma venting of lava layers, most of which precede Orientale by as much as O.5 Gy [15]. The production of such a long-lasting lava surplus seemingly requires a different explanation from that of ring and mascon production.
Figure 4: Nearside maria comprising the IC: Imbrium (A), Serenetatis (B), Crisium(C), Nectaris (D), and Humorum (E), are shown as ellipses. Solid curves denote their basalt-filled mountain ring “basins”, and dashed curves the approximate extent of ejecta fallout. Contiguous basalt flood plains (F-K) are shown by irregular shaded areas. Triangles indicate Apollo landing sites. Lunar Highlands (M) denote remainder (83%) of cratered lunar highlands. See Table 1 for mare specifications.
Note first, that the highest amplitude (bold) rings are all basalt filled. Their impact penetration depths, equated to their respective crater radii, (Table 1), plunge so deeply into the crustal matrix that the these craters actually penetrated the moon’s basalt mantle, 50 km beneath the surface. Thus, it is not surprising that researchers have found complete strata of crustal material down to the lunar mantle exposed in the Imbrium ejecta, including radioactive element abundances much higher than those found elsewhere on the lunar surface [16].
But these ejecta, laid down within a few minutes after impact, were succeeded by 10-50 kilometer waves, which virtually destroyed the fragile plagioclase crust to radii of 600-1,000 km within hours. Then followed untold eons of magma venting, up through the shattered crust, during which layer upon layer of basalt were deposited within the highest mountain rings. The dashed curves surrounding the maria correspond to the largest rings (Table 1: column 1). Mostly covered by ejecta from their respective impact craters, it is suggested that they mark the greatest extent of subsequent wave induced volcanism, as exemplified by extensive basalt lakes not identified as impact sites. For instance, the outer ring of Mare Imbrium clearly encompasses most of Mare Frigoris (F), Mare Vaporum (G), Mare Aestuum (G), and specific venting sources for the gigantic Oceanus Procellarum (P) [16]. Similarly, the outer rings of Maria Serenitatis (B), Crisium (C), and Nectaris (D) overlap Mare Tranquilitatis (H), and may contribute to Mare Fecunditatis (I). Lastly, Mare Humorum (E) abuts Maria Cognitum (J) and Nubium (K).
Like the basalts filling the maria basins, most of these extraneous deposits are multi-layered and appear to have been built up during the Late Imbrium Period (3.7-3.3 Ga) [17]. Progressive layering appears to have been a long cumulative process, in which local volcanic flux of lighter magma to the shattered surface was driven by sinking of the entire Imbrium complex, as evidenced by depression of the Procellarum region by about one km, and the Crisium region by about five km, below the equilibrium lunar surface [18].
Perception of the maria as solidified tsunamis reverses the usual course of scientific effort. Given an analytic solution in considerable detail, we here seek a convincing scenario that might have brought it about.
It is now widely accepted that the Maria were generated within the period 4.0-3.7 Gya by a “hailstorm” of objects from the asteroid belt, after a 400 my “rain” of billions of much smaller intra solar system debris that had brecciated the thin (10 km) plagioclase crust of the previously molten moon, which was then orbiting the earth at about half its present radius [19]. Only the largest impacts were sufficiently energetic to perforate the crust and plunge through its substrate, as evidenced today by the ejection of mantle basalts in various amounts, among which least 66 multi-ring structures have been catalogued as maria [12], or, in present context, frozen tsunamis.
To produce a cavity capable of collapsing into a wave system, as described above, the impact must penetrate the frangible crust and somehow produce, a quasi-fluid layer about 50 km deep, overlying a denser substrate capable of plastic uplift to form an anomalous mass concentration (mascon). The waves must also be high enough (10-30 km) to thoroughly brecciate 10 km of frangible crust so that it conforms to their underlying profile. According to Miles [2], the fluid layer can have an initial viscosity as high as 106 poises (104 Pa s) without affecting the dispersion pattern (wave spacing). Yet, most of the fluid layer must solidify within hours, seemingly at some threshold wave energy level, and yet remain supported on its underlying higher density substrate.
According to Bingham[ 20], crystalline colloids can undergo reversible solid-plastic-fluid transitions through shear-strain rupture of their crystal structure and their subsequent recrystallization. Liquid Kilauea basalts have been observed to solidify selectively at temperatures near 1,130 K by strain rate reduction [21], and yet to remain relatively fluid in an unstrained condition as low as 875 K [22]. The composition and temperatures of these basalts are close enough to those of early lunar subcrustal models [6] to expect cavity collapse, mantle uplift, and wave generation, if liquefied under sufficiently energetic impact conditions, and to suddenly resolidify upon degrading to some threshold Bingham shear strain rate. At depths below 200 km, radioactive heating might maintain the observed late stage lava venting for 1-2 billion years after the surface waves have solidified [6,16,17].
Thus, reconcilable computation models exist for all phases of the above-stated constraints, except for that of viscous-rubble rheology along the crust-mantle interface. Lacking facilities for such computations, I have prevailed upon others, whose ongoing computational simulations have satisfied most of the above constraints [7].
The perception of multi-ring maria as tsunamis with their underlying mantle uplifts (mascons), implies that during its heavy bombardment (≈ 400 – 370 Gya), and beneath its thin highly insulative, crust the moon was everywhere hot enough (1,200 – 1,300 K) to undergo massive Bingham fluidization, and subsequent venting decompression upon sufficiently energetic impacts, and to solidify superficially within hours to preserve surface waveforms. It also implies sufficient internal radioactive heating to maintain surface basalt venting for more than a billion years. These conclusions are consistent with a current lunar cooling model [23,24].
To: wvandorn@ucsd.edu (06/02/08)
Your suggestion we should be looking at non Newtonian “fluidization” after the passage of a shock wave through the rock has resulted in a lot of modeling to test the concept. Assuming that the moon rock behaves much like a viscous fluid, one can get the crater to rebound, make a jet which then collapses, sending out a few “waves” that finally freeze as result of the small amount of strength left in the pulverized crust. The results so far suggest that we have a valid model for reproducing your moon “tsunamis.” An mvi of these results is available. (Charles Mader, mccohi@aol.com) [7].