Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2017) Volume 7, Issue 5
Three theoretical expressions for the adsorption isotherms of hydrogen on Fe-Ti at three temperatures 100 K, 80 K and 60 K have been established. Our objective in this modeling is to select the adequate model that presents a high correlation with the experimental curves. The establishment of these new expressions is based on statistical physics formalism. This method has allowed the estimation of physicochemical parameters in the theoretical model. The parameters intervening in the adsorption process have been deduced directly from experimental adsorption isotherms by numerical simulation. We will mainly introduce three main parameters affecting the adsorption process, namely: the density of hydrogen receptor sites Nm, the number of molecules per site n and the pressure at half saturation P1 which characterizes the binding between the hydrogen and receptor sites on Fe-Ti. Then we apply the model to calculate the internal energies in an isothermal transformation, an isobaric transformation and an isosteric transformation.
<Keywords: Hydrogen; Statistical physics; Adsorption isotherm; Internal energy; Monolayer model
Hydrogen as an ideal energy carrier has attracted a great deal of attention in recent years. Its application in vehicles and portable electronics is limited by the difficulty of achieving a capable storage method [1]. For meeting the requirement of storability and portability, it is necessary to make the hydrogen storage in solid state. Therefore, the development of hydrogen storage compounds and the behavior of hydrogen in compounds have become focuses of both experimental and theoretical studies in recent years [2]. There are several hydrogen storage methods, including compressed gas, liquefaction, metal hydrides, and physisorption [3]. However, the main concern about its effective usage stems from the fact that it requires a complicated activation process, namely, high temperature treatment and high hydrogen pressure [4]. Despite numerous research efforts and many obvious developments, problems associated with the storage and transportation of hydrogen has remained unsolved. In the beginning, the metal alloys have been suggested as proper material for hydrogen storage [5]. Among different metal alloys, FeTi intermetallic powders are very promising media for reversible hydrogen storage [6] and has been selected for practical employment, because it is lighter and cheaper than other rare earth metals [7] and a hydrogen storage capacity around H/FeTi=1.9. Although more theoretical experimental works have been reported, many fundamental aspects of hydrogen adsorption are still an active field of research [8-10] and there is no sufficient theoretical interpretation for hydrogen adsorption on FeTi. Various mathematical empirical or semi-empirical models for the description of adsorption isotherms such Langmuir, Freundlich and many other models have been widely used in the several literatures works. These theoretical or empirical mathematical models are important since the first descriptions of the adsorption processes, based on these models are frequently used in literatures [11,12]. However, to describe accurately the adsorption isotherm empirical Langmuir and Freundlich models should be treated by statistical physics formalism to give an analytical expression in which physicochemical parameters are involved. In addition, this development allows us to interpret and to deduce information about physical adsorption at the molecular level which remains unapproachable by means of empirical methods. With these parameters (adsorption energy and receptor sites density), the adsorption process description is becoming very significant. This shows the importance of these models. The Langmuir-Fiendish model is more general than Langmuir or Frendlich models since it can give additional information about the number of adsorbed molecules per site. In this paper, our aim is to understand much better the hydrogen storage on Fe-Ti, the adsorption isotherm of molecular hydrogen was interpreted by the monolayer model with one energy, established by the statistical physics. One of the advantages of applying this theory is to give a physicochemical meaning to the parameters involved in the model and then to provide new interpretations of the adsorption process at molecular level. Then, using the thermodynamic theory of internal energy, the evolution of internal energies is studied in three deferent transformations: isotherm, isobar and isoster. The model has been applied for the first time to the adsorption isotherms of hydrogen molecules on Fe-Ti to allowed new physical interpretations at microscopic levels.
In order to treat the adsorption problem using the statistical physics method, we will perform with some assumptions as a basis of our calculations. Firstly, we consider that the adsorbed molecules are treated as an ideal gas. Since the mutual interaction between the adsorbed molecules will be neglected. Secondly, the freedom degree of vibration can be neglected in comparison with the translation degree [9,10]. Then, we consider that the rotational degree of freedom is neglected, since it is freezed in the solution.
The model supposes that a variable number of gas molecules are adsorbed onto N m receptor sites located on a unit mass of the adsorbent. The adsorption reaction of gas molecules (A) onto a receptor site (S) formed AnS adsorbed–receptor complex and should include a stoichiometric coefficient n as shown in the following equation:
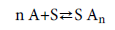 (1)
(1)
The n parameter as a stoichiometric coefficient represents the number of adsorbate molecules per site and is in general a whole or a fractional number but in our fitted values it could take any value, integer or not, since it is an average and it can also be greater or smaller than 1.
If n value greater than 1 it represents the number of anchored molecules per site, according to a multimolecular adsorption mechanism and if n is smaller than 1, it would represent the fraction of molecule per site [13-15]. The process is called a multi-anchorage adsorption. A multi-anchorage adsorption cannot be performed without considering a parallel position of the molecule to the adsorbent surface [14,15]. So, a multi-anchorage adsorption is also called a parallel adsorption. According to this hypothesis, 1/n would represent the anchorage number of one molecule on several different receptor sites [15].
In this treatment, the microscopic states of the adsorption process are described by using the grand canonical partition function. The receptor site is supposed to be empty or occupied by n molecules at a time. The state of occupation by a number Ni is defined by the situation in which this receptor site is placed. If Ni is 1, the site is occupied and if Ni is 0, the site is empty [10,11]. The grand canonical partition function zgc of one site is:
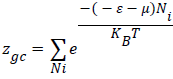 (2)
(2)
Where (-ɛ) is the receptor site adsorption energy, μ is the chemical potential of the adsorbed state and precisely of n adsorbed molecules, Ni is the receptor site occupation, β is defined as 1/KBT where KB is the Boltzmann constant and T is the absolute temperature in Kelvin.
The total grand canonical function related to Nm receptor sites per unit mass, which we assume independent and identical, is equal to:
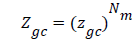 (3)
(3)
This total grand canonical partition function allows us to determine the average site occupation number No which can be written as [10,12]:
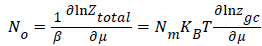 (4)
(4)
When the thermodynamic equilibrium is reached, the equality related to the chemical potential equilibrium, which expresses the mass action law, can be written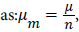 where μ is the chemical potential on a site, n is the number or fraction of molecule(s) per site, and μm is the chemical potential of a whole molecule.
where μ is the chemical potential on a site, n is the number or fraction of molecule(s) per site, and μm is the chemical potential of a whole molecule.
In the case of the approximation of an ideal gas, the chemical potential can be written as [13]:
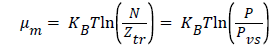 ( 5)
( 5)
Where P is the pressure at equilibrium, Pvs is the saturated vapor pressure and Ztr is the translation partition function of the adsorbed molecule which is defined by this expression:
With m being the adsorbed molecule mass, V the volume of the system and h the Planck’s constant.
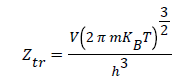 (6)
(6)
In the case of n molecules anchored per site the total number of adsorbed molecules Na is given by:
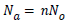 (7)
(7)
Isotherm equations of the simulation models
Monolayer model (Hill): A receptor site can be assumed to be either empty or occupied by one or more molecules. Thus, the grand canonical partition function calculated for one site is written [14-18].
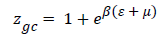 (8)
(8)
Where is the receptor site adsorption energy level of one receptor site, m is the chemical potential of the adsorbed molecule, and b is the Boltzmann factor. The average number of the occupied receptor sites calculated from Eq (8) and (4) is to be further simplified [14-18] in order to obtain:
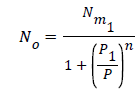 (9)
(9)
Where P1 is the pressure at half saturation.
Finally, the number of adsorbed hydrogen molecules as a function of pressure is given by the following expression [18]
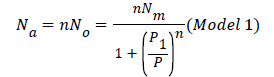
By simulating an isotherm with this relation, four parameters can be fitted: the number of molecules per site (n), the density of hydrogen molecules receptor sites Nm, the pressure at half saturation P1 and the adsorbed coverage θ. The monolayer amount of adsorbed molecules can be deduced by this relation Q=nNm.
Monolayer model with two energies: We consider that a variable number of molecules Na are adsorbed onto two types of independent sites. The number of the first type sites per unit mass is Nm1 and the number of the second type is Nm2. We suppose that the adsorption onto the first type is carried out with an energy (-ɛ1) and onto the second type with an energy (-ɛ2). In this case, the total grand canonical partition function can be written as follows if we consider the two sites are independent:
partition function can be written as follows if we consider the two sites are independent:
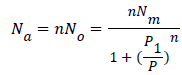 (10)
(10)
With z1gc and z2gc being the partition functions of the two types of site; they are expressed by the following relations:
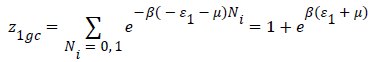 (11)
(11)
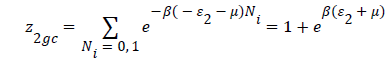 (12)
(12)
Where μ are the chemical potential son site, respectively, and Ni is the number of occupation.
Using the previous definition of occupation number, the total number of occupied sites is:
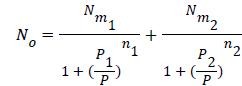 (13)
(13)
Where n1 and n2 are the number of molecules per site, corresponding to the first and the second receptor sites respectively. Using Eq.(7) we obtain the expression of the number of adsorbed hydrogen molecules versus the pressure [19].
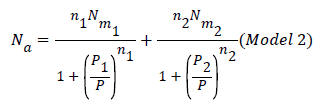
Double layer model with two energies: The adsorption on the first layer is assumed at an ε1 adsorption energy level and the adsorption on the second layer at a different ε2 adsorption energy level which should be lower than ε1 (as the first adsorbed layer interacts directly with the surface sites at the highest energy). The partition function developed for either empty or occupied sites can be written as follows:
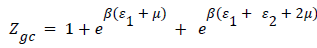 (14)
(14)
The expression of the double layer model with two energies can be written after simplifications as the following expression [20].
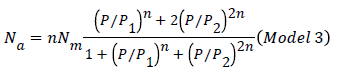
Our objective in this modeling part is to select the adequate model, which presents a high correlation with the experimental data. We have adjusted the experimental curves with the expressions of three different established models based on statistical physics treatment like monolayer with one energy (Hill model) (Model 1), monolayer with two energies (Model 2), and double layer with two energies (Model 3), and in terms of comparison with these statistical physics models, our isotherms have been fitted also by two known models like Langmuir and Freundlich.
In general, the choice of the appropriate model is based first numerically on the values of the adjustment coefficient R2 corresponding to the model and which is given by numerical simulation. But also, physical consideration must be taken into account for this choice. We note that the experimental curve shows a high correlation with the proposed model whenever the adjustment coefficient R2 is close to unit. In Table 1 we present the adjustment correlation coefficients of the four-treated model for all three temperatures.
| T(K) | (Model 1) | (Model 2) | (Model 3) | Langmuir | Freundlich |
|---|---|---|---|---|---|
| 60 | 0.999 | 0.997 | 0.97 | 0.87 | 0.78 |
| 80 | 0.998 | 0.987 | 0.978 | 0.94 | 0.86 |
| 100 | 0.999 | 0.988 | 0.985 | 0.78 | 0.75 |
Table 1: Values of R2 adjustment coefficient of each model.
Choice of adequate model
Based on the calculated adjustment coefficients given for each model, we can draw some conclusion on the variation of these coefficients.
The fitting mathematical method was based on the Levenberg- Marquardt iterating algorithm using a multivariable non-linear regression. The best fitting result has been established once the residuals between the experimental data and values predicted by the model were minimized according to a 95% level of confidence. The monolayer model with one energy presents the highest R2 values (from 0.998 to 0.999), compared to the other models. However, these values were close to the R2 values of the model 2 in the range of 0.997-0.998. So, we can investigate that the variation of the coefficient of correlation R2 was not a significant parameter to define the best model. Indeed, the adjusted physicochemical parameters values should be physically acceptable and should facilitate the interpretation of the adsorption process.
In term of comparison between the values of physicochemical parameters of the model 1 and the model 2, it seems that the values of the model 2 have not to take into account its physical meaning. Consequently, the model 1 was considered as the adequate model to describe and to interpret the adsorption process of the experimental isotherms of Hydrogen on Fe-Ti.
The fitting of the experimental isotherms of hydrogen on Fe-Ti at all temperatures: 100 K, 80 K and 60 K (Figure 1) exhibits a good adequation between the model 1 curve and the experimental data. The theoretical curves are presented in Figure 1.
Figure 1: Adsorption isotherms of hydrogen molecules on Fe-Ti at three various temperatures: T=100 K, T=80 K and T=60 K. The squares, circles and triangles are the experimental data [21] and the red lines are the simulation data.
Three physicochemical parameters such as a number of molecules per site n, the density of a receptor site Nm and the pressure at half saturation P1 have been directly obtained from the fitting of the experimental adsorption isotherms by numerical simulation. These parameters are related to the adsorption process and introduced in the analytical model expression of the adequate model. There are two categories of parameters [15]. On one hand like: n and Nm are parameters showing the anchorage properties between adsorbed hydrogen gas and receptor sites according to the geometry of the hydrogen molecules. On the other hand, energetic parameter like P1 is giving the adsorption energy which characterizes the binding between the hydrogen molecules and receptor sites on Fe-Ti. These parameters are resumed in Table 2.
| T(k) | n | Nm | Q=nNm | θ | P1 (MPa) |
|---|---|---|---|---|---|
| 60 | 1.55 | 2.5 | 2.32 | 1.5 | 32.7 |
| 80 | 1.6 | 1.9 | 3.04 | 3.4 | 45 |
| 100 | 1.4 | 1.5 | 3.5 | 5.7 | 25.5 |
Table 2: Fitting results of experimental data with the model 1.
Stereographic interpretations
In this section we are going to try to interpret the adsorption isotherms by the model parameters. The usefulness of the parameters meaning plays in general a main role to much better understand the adsorption process of hydrogen. Thus, the evolution of such parameters as a function of experimental conditions will be investigated in great details in order to interpret and understand the physical process at the molecular level. In this way, two interpretations, steric and energetic are derived.
Number of hydrogen molecules per site n: The n stoichiometric coefficient value gives information about the orientation of the molecule with respect to the adsorbent surface. In fact, the molecule has several manners to be anchored on the receptor site according to its geometry and its angle of incidence with the adsorbent surface. We figured in Figure 2 the number of hydrogen molecules per sites in function of the temperature, calculated with model 1. We have noticed that the number of adsorbed molecules per site, n at three different temperatures is always greater than unity for the hydrogen. This means that the hydrogen molecules might be anchored either by one molecule per site or by two molecules per site. So, the adsorption of hydrogen molecules would be a multimolecular adsorption in this case. The Figure 2 shows that the temperature has a strong influence on the stereography of the adsorption process. This parameter increased with temperature and then decreased at the highest temperature. The increase can be due to the appearance of some hidden receptor sites and the decrease can be probably attributed to the decrease in the density of receptors sites Nm with temperature.
Density of receptors sites Nm: The variation versus temperature of the receptor sites density (Nm) which is proportional to the adsorbed quantity Q is reported in Figure 3. The receptor sites density of hydrogen molecules has decreased with temperature. This evolution is due to the tendency to aggregation. This aggregation could hinder the accessibility to the adsorption receptor sites for the molecules of hydrogen.
The amount of adsorbed molecules Q: The amount of adsorption quantity depends on the number of molecules per site and the density of receptor sites Nm which represents the ability of the surface of Fe-Ti to retain hydrogen molecules. In Figure 4 the evolution of this parameter versus the temperature is reported. It can be noticed that the temperature has had a significant effect on the amount of adsorption quantity. Indeed, the increase in the temperature has led to increase in the amount of adsorbed hydrogen molecules. This is due to the endothermic nature of adsorption which is not usual in a classical adsorption phenomenon.
Adsorption energies: Using the values of the parameters P1, and Pvs we have calculated the molar adsorption of energies at three temperatures 100 K, 80 and 60 K using this following equation:
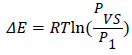 (15)
(15)
Where R = 8.314472 J/mol k is the ideal gas constant and PVS is determined by the following expression [16].
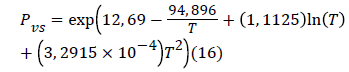
This energy inform us about the interaction between hydrogen molecules and the surface. We note that the values of calculated energies at three temperatures allow supporting the fact that binding between molecules and surface takes place via a physical adsorption (Vander Waals interactions, or hydrogen binding), since, the different values were less than 40 kJ/mol [8]. In Table 3 we present the values corresponding to the energies of adsorption for each adsorption isotherm.
| T(k) | Pvs (P) | E(kJ/mol) |
|---|---|---|
| 60 | 2.0753107 | 4.6663 |
| 80 | 1.06648108 | 11.822 |
| 100 | 5.6672108 | 29.7 |
Table 3: Values corresponding to the molar adsorption energies.
Evolution of internal energy in an isothermal process, an isobaric process and an isosteric process.
In order to understand the influence of those three main parameters like temperature, pressure and number of adsorbed molecules Na, on the evolution of internal energies during the adsorption hydrogen mechanism, we suggested three different transformations of our system: an isothermal process, an isobaric and an isosteric process. The total number of hydrogen molecules in our system is defined as follows: N=Ng+Na within Ng is the number of hydrogen gas molecules in the free phase and the Na is the number of adsorbed hydrogen molecules in the adsorbed phase.
Internal energy in an isothermal process: Internal energy (Eint) is, defined by the total energy forms present within a system in isotherm process. It is particularly due to existing interactions between the adsorbate particles of the system and the adsorbent. The energy of the system is given by the following relation:
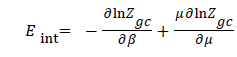 (17)
(17)
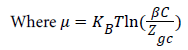
The total internal energy of our system is defined as follows:
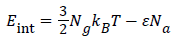 (18)
(18)
Where 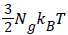 is the energy of hydrogen gas molecules in a free phase and εNa is the adsorbed energy of hydrogen molecules in an adsorbed phase. Finally using the expression of model 1 the total internal energy can be written as:
is the energy of hydrogen gas molecules in a free phase and εNa is the adsorbed energy of hydrogen molecules in an adsorbed phase. Finally using the expression of model 1 the total internal energy can be written as:
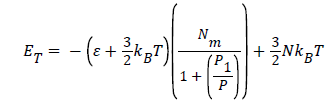 (19)
(19)
In this, isothermal transformation, the temperature is an unvaried parameter, however, the two parameters pressure P and number of adsorbed hydrogen molecules Na have been varied in this process.
Figure 5 shows, that the values of the isothermal internal energy are decreased algebraically with the increase of the pressure, however, they are increased in absolute value. This is due to the increase of the amount of adsorption quantity with the pressure during this process. Moreover, we have suggested that the maximum stored hydrogen energy attained in absolute value of energy around 2 kJ. Here, we have deduced that it is necessary to increase the pressure to attain the maximum stored hydrogen energy. This evolution of isothermal internal energy can confirm the physisorption phenomenon which explains that our system has not yet attained the saturation of storage hydrogen molecules on Fe-Ti [22].
Internal energy in an isobaric process
In this isobaric transformation, the internal energy has the following expression:
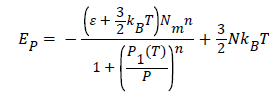 (20)
(20)
The evolution of the internal energy in this case is depending only to the temperature and number of adsorbed hydrogen molecules Na, however, the pressure is unvaried parameter during this process. From Figure 6, we notice that the isobaric internal energy increased algebraically and decreased in absolute value. Moreover, the disorder increases with the increasing of temperature, thereby, the isobaric internal energy tends to zero [23].
Internal energy in an isosteric process
During this transformation, the number of adsorbed molecules Na has been varied, that means the adsorption process isn’t considered during this process, however, the temperature and the pressure are considered like varied parameters and they are proportionally related. Here, the internal energy is defined by this following equation:
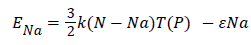 (21)
(21)
In Figure 7 we suggested that the internal energy increases approximately linearly in the lowest pressure region and then remains constant in the highest-pressure region. This negative energy has been attributed not only to the isosteric transformation energy but also to the energy of agitation gas in the free state.
In summarize, to use the grand canonical ensemble in statistical physics and to apply some simplifying approaches, we have established three theoretical expressions to fit the adsorption isotherms of hydrogen on, Fe-Ti alloy at 100 K, 80 K and 60 K. These models are thermodynamically consistent and the physicochemical parameters intervening in the adsorption process have been taken account into the theoretical treatment. It has been found that the proposed statistical treatment is sufficiently flexible to give a good representation of the experimental data. The appropriate model for fitting the different adsorption isotherms was a monolayer model with one energy (Hill). The study of the parameter n shows that the anchorage of hydrogen molecules on the receptor sites will would be a multi-anchorage. The evolution of the two parameters n and the density site receptor Nm with the temperature have proven the presence of the aggregation phenomenon. The study of the evolution of amount adsorbed molecules indicates that the adsorption process of hydrogen molecules is endothermic. The tree parameters like: T, P, Na have been found to have a significant effect on the evolution of internal energy in three different transformations: an isobaric transformation, an isosteric transformation and an isothermal transformation.
The Langmuir model is a particular case of the Hill model, n takes the value of the unit
The expression is defined as:
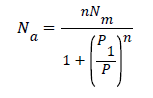 − (A1)
− (A1)
The Freundlich model is itself a particular case of Hill model but with very low pressure. The model expression becomes:
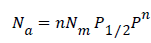 − (A2)
− (A2)