Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2016) Volume 6, Issue 2
The influence of localized charge distributions at the interfaces of spherical colloidal particles in aqueous suspension is discussed in the light of the effective medium approximation theory of heterogeneous systems. The approach is shown to give analytical results in the case of shelled particles with the presence of two distinct interfaces. The whole dielectric response of the system gives rise to different relaxation contributions, falling in different frequency regions and attributed to different polarization mechanisms, at a molecular level. In particular, the number and the strength of the dielectric relaxations associated with the presence of localized charges is discussed.
<Keywords: Dielectric relaxation; Colloidal particles; Biological cells; Charge-induced polarization
The dielectric relaxation spectra of aqueous suspension of spherical colloidal particles, covering an exceptional wide frequency window, reflect the occurrence of different relaxation mechanisms which interest different regions of the whole system, from the polarization of the ionic atmosphere, at lower frequencies, to the interfacial polarization at intermediate frequencies, up to the orientational polarization of the aqueous medium at higher frequencies.
These different relaxation regions generally present a complex structure, being due to more than a single dielectric mechanisms that partially overlap. This exceptional rich phenomenology, if on one side offers the possibility of investigating what happens in the presence of an external electric field, on the other hand, makes the interpretation of the dielectric spectra of colloidal particle aqueous suspensions rather difficult and, in some cases, questionable.
The general problem we facing with when we are dealing with the analysis of a dielectric relaxation spectrum is that of separating the influence of the different polarization mechanisms, at a molecular level, assigning to each of them a particular relaxation region together with the extraction of the dielectric parameters which govern that particular polarization mechanism.
In this note, we will treat, in a rather general scenario, the influence of charge distributions localized at the particle surface on the dielectric spectra of charged colloidal particle suspensions. We will consider a composite spherical particle built up by a core covered by a concentric shell bearing at each of its boundaries a superficial charge distribution. Charges are constrained to move on the surfaces under the gradients of the electrical potential and the charge density. We will do this taking advantage of the dielectric model proposed by Prodan et al. [1] some years ago to describe the dielectric behavior of spherical live cell in suspension, assuming the presence of charge distributions at the outer and inner faces of the cell membrane. These charge distributions have been introduced by Prodan et al. [1] and Bot et al. [2] to justify in a quantitative way the presence of the membrane potential in biological cells, whose value is related to the conductivity of the superficial charges through the relationship
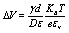 (1)
(1)
where γ is the surface conductivity of ions with diffusion coefficient D moving at the surface of a medium of permittivity ε, d is the membrane thickness and e is the elementary charge and KBT the thermal energy and ev the dielectric constant of free space.
However, the same picture can be applied to any colloidal particle characterized by an internal core covered by a concentric shell with a localized charge distribution at each of the two interfaces. The model is rather general and can be applied to a variety of different colloidal particles by simply defining, from a dielectric point of view, their relevant electrical and/or geometrical parameters. They are the permittivities ek and the electrical conductivity sk (k=0,1,2) of each of the dielectric medium that describes the system from an electrical point of view and the surface conductivity γ and the diffusion coefficient D that characterize the electrical polarization of the surface charge distributions.
The general solution of the dielectric problem can be obtained, in the light of the effective medium approximation theory, from the solution of the Laplace equation in the dipolar approximation (far-field approximation) with the appropriate boundary conditions, that, in this case, beyond the usual electrical and geometrical constrains, must take into account the presence of the two localized charge distributions at the particle interfaces.
In the case of particles dispersed in an aqueous solution of moderate to high electrical conductivity, such as for example biological cell suspensions, the Debye screening length may be rather small (of the order of 0.5 nm for bulk ionic concentration of about 0.15 mM). In these systems, we expect a uniform ionic distribution outside the membrane particle, except in a very thin layer close to the membrane itself, with a thickness of the order of some Angstroms. Consequently, the model is particularly suitable to describe the dielectric behavior of a biological cell suspension and the numerical simulations have been carried out considering values of the electrical parameters typical of these systems.
Our results furnish the full description of the whole dielectric spectrum of charged colloidal particles in aqueous suspension. In particular, the present analysis predicts the presence of some unexpected and interesting results, for instance the ones concerning the role played by the charge distributions and their shielding effects, providing valuable information for the interpretation of experimental data.
We will consider a spherical particle of complex dielectric constant 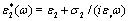 , radius R2, covered by a concentric shell of complex dielectric constant
, radius R2, covered by a concentric shell of complex dielectric constant  and thickness d = R1- R2 and dispersed in an aqueous medium of complex dielectric constant
and thickness d = R1- R2 and dispersed in an aqueous medium of complex dielectric constant 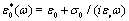 Here, ω is the angular frequency of the applied external electric field.
Here, ω is the angular frequency of the applied external electric field.
At each of the two interfaces, i.e., the outer and inner shell surfaces (of radii R1 and R2, respectively), the presence of two localized charge distributions ρ1 and ρ2, being the charges obligated to move at the membrane surfaces, produces two surface current densities described by
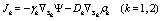 (2)
(2)
Here, γk and Dk are the surface conductivities and the diffusion coefficients, respectively, of the bound charges at the two interfaces Sk.
This model is appropriate enough to describe, by a dielectric point of view, a biological cell, at least in a spherical geometry, where the particle core models the cytosol, the shell models the cell membrane and the aqueous medium the extracellular medium. Moreover, the surface currents generated by the surface charge distributions assume a biological meaning since they influence the membrane potential ΔV, as extensively discussed by Bot and Prodan [2,3]. Finally, in biological cells, the surface charge distributions are originated by the effective membrane structure where the presence of small charged molecules and a variety of organic ions free to move in the direction tangential to the membrane surface with the consequent increase of the tangential membrane conductivity. However, the same model yields to describe, in a rather general way, the behavior of any colloidal particle in aqueous suspension and most of the results obtained in the biological framework can be transported in the colloidal one by simply changing the meaning of the characteristic parameters.
A sketch of the above stated dielectric model is shown in Figure 1.
The presence of the two charge distributions produces a rather intricate dielectric response and the dielectric spectra show at least two different relaxation regions. They are located, the first (named α-dispersion), in the low-frequency range and is due to the polarization induced by the bound charge distributions, and the second (named β-dispersion), located at higher frequencies and due to the usual Maxwell-Wagner effect, typical of highly heterogeneous systems. The interplay between the two above stated dispersions, when the values of the electrical parameters of the different media involved cause a more or less overlap, is basically the origin of the complexity of the dielectric response of a colloidal particle suspension.
Moreover, this partial overlap makes the deconvolution of the spectra difficult and in some cases prejudices the correct extraction of the values of the dielectric parameters (in the case of a biological cell, the membrane permittivity and the membrane conductivity).
In the light of the mean-field approximation, the complex dielectric constant ε*(ω) of a collection of dielectric objects uniformly dispersed in a continuous phase is given by
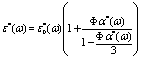 (3)
(3)
Where Φ is the particle volume fraction (defines as Φ =Nvp/Vtot, with vp the volume of each particle at the numerical concentration N/Vtot) and α*(ω) is the frequency dependent polarizability defines as
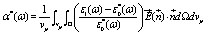 (4)
(4)
where 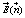 is the total electric field acting on the single dielectric object with direction
is the total electric field acting on the single dielectric object with direction  and dΩ indicates the solid angle element generated by direction
and dΩ indicates the solid angle element generated by direction  . The evaluation of the electrical polarizability α*(ω) is the main roblem of our task.
. The evaluation of the electrical polarizability α*(ω) is the main roblem of our task.
Polarizability α*(ω) for a generically shaped dielectric particle
The determination of the electrical polarizability α*(ω) of a particle requires solving the electrostatic problem where the particle is in a uniform applied electric field  . In the present case, besides the surface charge density polarization σp at the interface due to the mismatch of the complex dielectric constants (the polarizations which originates the classical Maxwell-Wagner effect), we have to consider the localized charge density distribution σl, once the equilibrium is attained, due to the charges bounded to the particle surfaces. Taking into account the polarization charge distribution and that the difference of the normal component of the electric displacement at the interface must equal the localized surface charge density, the total contribution at the interface can be written as
. In the present case, besides the surface charge density polarization σp at the interface due to the mismatch of the complex dielectric constants (the polarizations which originates the classical Maxwell-Wagner effect), we have to consider the localized charge density distribution σl, once the equilibrium is attained, due to the charges bounded to the particle surfaces. Taking into account the polarization charge distribution and that the difference of the normal component of the electric displacement at the interface must equal the localized surface charge density, the total contribution at the interface can be written as
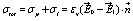 (5)
(5)
where 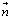 and
and 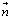 are the electric fields outer and inner the dielectric particle, respectively and
are the electric fields outer and inner the dielectric particle, respectively and 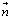 is the unit normal vector directed outword the interface.
is the unit normal vector directed outword the interface.
Consequently, the total potential 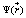 , due to the sum of the surface charge contributions (localized charge and polarization charge distributions), takes the form
, due to the sum of the surface charge contributions (localized charge and polarization charge distributions), takes the form
 (6)
(6)
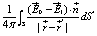
By applying the Gauss theorem, in the absence of bulk charge distribution, the potential can be written as an integral over the volume V of the particle
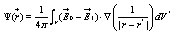 (7)
(7)
and, in the dipolar approximation, the polarizability α*(ω) of the particle is given by
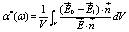 (8)
(8)
Equation 8, depending on the electrical fields outside and inside the the particle generated by the applied electric field  , represents the general expression of the polarizability of a generic particle.
, represents the general expression of the polarizability of a generic particle.
In the absence of localized surface charge distribution, equation 8 reduces to
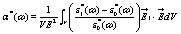 (9)
(9)
taking the form of a weighted average with weight given by the difference in the permittivities between the media inside and outside the particle.
In this framework, the dielectric problem is turned into the calculation of the polarizability α*(ω) (equation 4). Following the procedure suggested by Sebastian et al. [4,5], this quantity can be written as
 (10)
(10)
This general expression includes the case in which an electrical charge distribution is present at the particle interfaces, through the addition of the term in the volume integral of equation 10.
The problem of the polarizability of a shelled sphere (and also of shelled particles of arbitrary shape) has been recently considered by Sebastian et al. [4,5] who show that, within the dipolar approximation, the complex polarizability of shelled particles can be written as an appropriate weighted average of the electric field inside the particle, where the weights are determined by the differences in the complex dielectric constants between the different adjacent dielectric media involved in the construction of the cell. Also in this case, however, these authors limited ourselves to the charge distributions originated at the interfaces under the influence of the external electric field, without considering any added (localized) charge distributions.
In the present case, besides the surface charge polarizations at the two interfaces due to the mismatch of the complex dielectric constants (the polarization which originates the classical Maxwell- Wagner effect), we have to consider the localized charge distributions, once the equilibrium is attained, due to the charges bounded to the two membrane surfaces. Taking into account the polarization charge distribution and that the difference of the normal components of the electric displacement at any interface must equal the localized surface charge density, the two total contributions at the two interfaces can be written as
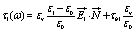 (11)
(11)
at the surface of radius R1 and as
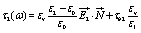 (12)
(12)
at the surface of radius R2, respectively. Here, τb1 and τb2 are the surface charge distributions at the two membrane interfaces of radius R1 and R2, respectively.
Consequently, the total potential, as the sum of the two surface charge contributions (localized charge and polarization charge distributions), takes the form
 (13)
(13)
The two charge distributions τb1 and τb2 can be written, according to the derivation of Prodan et al. [1], as a function of the external electric field 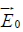 , in the form
, in the form
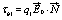 (14)
(14)
 (15)
(15)
where q1 and q2 are given by equation 30 of the work by Prodan et al. [1].
Following the procedure proposed by Sebastian et al. [4,5], equation 13 becomes
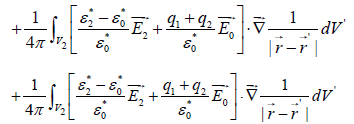 (16)
(16)
By comparing equation 16 to the potential created by a dipole in vacuum, the polarizability α*(ω) can be written as
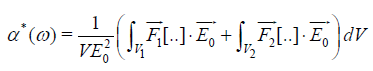 (17)
(17)
where the functions 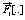 and
and 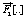 are given by
are given by
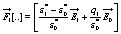 (18)
(18)
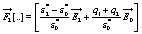 (19)
(19)
The knowledge of the electric fields 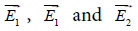 furnishes the total polarizability of the shelled particle in the presence of the localized charged distributions and, according to equation 4, the complex dielectric constant of a collection of these composite particles uniformly distributed in an aqueous medium.
furnishes the total polarizability of the shelled particle in the presence of the localized charged distributions and, according to equation 4, the complex dielectric constant of a collection of these composite particles uniformly distributed in an aqueous medium.
A further comment is in order. Equation 19 contains the term ∇2Ψ that is lacking in the original work by Prodan et al. [1]. This term corrects some inconsistences found in the original derivation of these authors. We have discussed in detail this important point in an our previous work [6,7].
Finally, although equation 3 has been derived for spherical particles in the limit Φ = 1, it can be employed for non-spherical particles too, provided that the fractional volume is maintained moderately low, widening the applicability of this model to differently shaped dielectric objects.
The shelled sphere: the electrical fields
The electric field inside and outside the particle is obtained by solving the Laplace equation for the electrical potential Ψ. In spherical coordinates (r,θ,?), the general solution of the Laplace equation ∇2Ψ =0 is given by
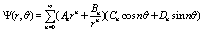 (20)
(20)
The solution for a uniform electric field  applied along the x-axis, because the axial symmetry, is much simpler and can be read as
applied along the x-axis, because the axial symmetry, is much simpler and can be read as
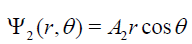 (21)
(21)
for r > R1 and
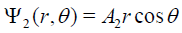 (22)
(22)
for r < R2, and
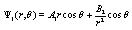 (23)
(23)
for R2 < r < R1 where the constants A1, B1, A2, and B2 are appropriate constants to be determined through the boundary conditions. They imply that the potential must be continuous across the boundary (for r = R1, r = R2) and the displacement in the normal direction to the boundary surfaces must obey to the condition
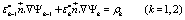 (24)
(24)
where the quantities ρk must satisfy the conditions
 (25)
(25)
After some cumbersome algebra, the constants A1 and B1 are given by
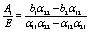 (26)
(26)
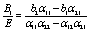 (27)
(27)
where the quantities αij and bi are defined as
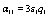 (28)
(28)
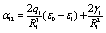 (29)
(29)
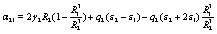 (30)
(30)
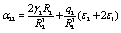 (31)
(31)
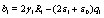 (32)
(32)
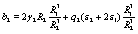 (33)
(33)
where qk are defined as
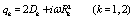 (34)
(34)
Finally, the other constants that define the potentials are given by
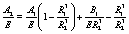 (35)
(35)
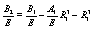 (36)
(36)
The knowledge of the coefficients A1, B1, A2, and B2 allows the electric fields to be completely defined and consequently the polarizability α*(ω) can be obtained and hence, from equation 3, the whole dielectric relaxation of the system.
In the following, we will present some characteristic spectra over a wide enough frequency range, paying attention to the role played by the localized surface charge distributions in the whole dielectric response of the system.
The typical spectrum of the dielectric permittivity ε´(ω) and the electrical conductivity σ(ω) as a function of frequency of the applied electric field of a suspension of spherical shelled particles (fractional volume Φ =0.10) is shown in Figure 2.
Figure 2: Permittivity ε´(ω) of a concentric shelled spherical particle suspension as a function of the frequency for localized surface charge distributions γ1=γ2=1 × 10-9. The dielectric phase parameters are: Φ=0.10, ε0=80, σ0=0.0001 mho/m; ε1=20, σ1=106 mho/m; ε2=10, σ2=1 × 107 mho/m. The charge diffusion coefficients are varied from D1 = D2=10-10, 10-9, 10-8, 10-7 and 10-6 m2/s, (marked in the increasing order by the arrow). The sphere is modeled with R1=10-6 m, R2=0.5 × 10-6 m. The inset shows the electrical conductivity σ(ω) as a function of frequency, for the same set of values of the parameters. The numbers represent SI units.
Depending on the choice of the values assumed by the dielectric phase parameters, at least two different dielectric relaxation regions appear, falling in well-separated frequency range. The first is unequivocally attributed to the polarization effect induced by the charge motion at the particle membrane surfaces, which adds to the usual Maxwell-Wagner polarization, due to the mismatch in the dielectric properties of the media adjoining the interfaces. This latter relaxation occurs in the higher frequency range without overlapping, because of the values of the parameters employed, with the relaxation at lower frequencies. However, in some cases, for particular values of the dielectric phase parameters, the two relaxation partially overlap. This situation may lead to serious problems in the deconvolution of the entire spectrum when the values of the dielectric parameter (or only some of them) must be evaluated from the whole spectrum. In this case, in the fitting procedure, one is obliged to take into consideration the whole spectrum and the analysis of the data must necessarily involve the contribution of the surface charge distribution.
The influence of the surface charge distributions at the two interfaces on the whole dielectric response of the system is shown in Figures 3 and 4, where the dielectric spectra (the permittivity ε´(ω) and the electrical conductivity σ(ω) in two different extreme cases, i.e., γ1 =0 and γ2 varied from γ2=10-11 to γ2=10-8 and γ2=0 and γ1 varied from γ1=10-11 to γ1=10-8, are reported. The numerical values are given in SI units.
Figure 3: Permittivity ε´(ω) of a concentric shelled spherical particle suspension as a function of the frequency for a localized surface charge distributions characterized by γ1 =0, for different values of γ2 (1 × 10-11, 5 × 10-11, 1 × 10-10, 5 × 10-10, 1 × 10-9, 5 × 10-9, 1 × 10-8, marked in the increasing order by the arrow). The dielectric phase parameters are: Φ=0.10, ε0=80, σ0=0.0001 S/m; ε1=20, σ1=10-6 S/m; ε2=10, σ2=1 × 10-7 S/m. The charge diffusion coefficients are assumed to be D1 = D2=10-8. The sphere is modeled with R1=10-6 m, R2=0.5 × 10-6 m. The inset shows the electrical conductivity σ(ω) as a function of frequency, for the same set of values of the parameters. The numbers represent SI units.
Figure 4: Permittivity ε´(ω) of a concentric shelled spherical particle suspension as a function of the frequency for a localized surface charge distributions characterized by γ2 =0, for different values of γ1 (1 × 10-11, 5 × 10-11, 1 × 10-10, 5 × 10-10, 1 × 10-9, 5 × 10-9, 1 × 10-8, marked in the increasing order by the arrow). The dielectric phase parameters are: Φ=0.10, ε0=80, σ0=0.0001 S/m; ε1=20, σ1=10-6 S/m; ε2=10, σ2 =1 × 10-7 S/m. The charge diffusion coefficients are assumed to be D1 = D2=10-8. The sphere is modeled with R1=10-6 m, R2=0.5 × 10-6 m. The inset shows the electrical conductivity σ(ω) as a function of frequency, for the same set of values of the parameters. The numbers represent SI units.
As can be seen, the dielectric response is rather different in the two cases, evidencing how the surface charge distributions exert a different effect not only in dependence of their magnitude but also in dependence of their geometrical localization. These results make even more evident the fact that the shielding effect of the external surface charge distribution is partial and that the influence of the inner charges even in presence of outer charges cannot be neglected. In order to make more evident this mutual interconnection between the different charge distributions present in the system, in Figure 5, we show a panel where the permittivities and the electrical conductivities for γ1=0 and two extreme values of γ2 and for γ2=0 and two extreme values of γ1 are collected together.
Figure 5: Permittivity ε´(ω) and electrical conductivity σ(ω) of a concentric shelled spherical particle suspension as a function of the frequency with the presence of a single localized surface charge distribution localized alternatively at the inner or outer interface. Left panels: Low values of γ (γ =5 × 10-11) at the outer or at the inner interface. Upper panel: the permittivity ε´(ω); bottom panel: the electrical conductivity σ(ω). Insets show the dispersion curves in an enlarged scale. Right panels: high values of γ (γ =5 × 10-9) at the outer or at the inner interface. Upper panel: the permittivity ε´(ω); bottom panel: the electrical conductivity σ(ω). The dielectric phase parameters are: Φ=0.10, ε0=80, σ0=0.0001 S/m; ε1=20, σ1=10-6 S/m; ε2=10, σ2=1 × 10-7 S/m. The charge diffusion coefficients are assumed to be D1 = D2=10-8. The sphere is modeled with R1=10-6 m, R2=0.5 × 10-6 m. The numbers represent SI units.
As can be seen, the influence of the charge localization (on the outer or on the inner interfaces of the shelled particle) is rather marked, depending on its absolute value. For instance, when the value of γ is low (of the order of γ =5 × 10-11), the localization of the charge distribution on the inner or outer interface does not influence markedly the dielectric response, neither in the permittivity ε´ nor in the electrical conductivity σ(ω), (Figure 5, left panels). On the contrary, when γ is moderately high (of the order of γ=5 × 10-9), the charge localization produces a rather different dielectric response, (Figure 5, right panel). In particular, in the second case, when the the external distribution is absent, the charge distribution at the inner surfaces gives rise to a further relaxation region, which is absent in the opposite case. This behavior is a clear example of the shielding effect of a charge distribution on the appearance of a dielectric relaxation in the whole dielectric spectrum.
The number of interfaces and the associated dielectric relaxations in heterogeneous systems has been discussed many years ago by Hanai et al. [8], who stated that the dielectric relaxations are equal to the interfaces in the number. This sentence is rigorously correct in the absence of any localized charge distribution, the surface charge being due to the interfacial polarization effect. On the contrary, when charges originated by different effects are also present, as in the cases we have simulated in the present note, the situation is even more intrigued, the whole effect depending on the geometrical charge localization too.
On the basis of the Prodan et al. model [1], in the light of the effective medium approximation, we have investigated the influence of localized charge distributions at the interfaces of spherical shelled particles dispersed in aqueous solution on the dielectric relaxation spectra, over a wide frequency range.
The system described in this note is appropriate enough to model the dielectric behavior of biological cell suspensions, where the membrane potential is originated by the presence of charge distributions at the membrane interfaces. In this case, we show how the high-frequency relaxation due to the Maxwell-Wagner effect is influenced by the low-frequency relaxation region caused by the presence of interfacvial localized charge distributions. The partial overlap of these two relaxation regions may cause uncertainties in the derivation of dielectric phase parameters from dielectric spectra of such highly dispersed heterogeneous systems.