Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2017) Volume 6, Issue 3
Current Federal Aviation Administration regulations require that passing aircraft must either meet a specified horizontal or vertical separation distance. However, solving for optimal avoidance trajectories with conditional inequality path constraints is problematic for gradient-based numerical nonlinear programming solvers since conditional constraints typically possess non-differentiable points. Further, the literature is silent on robust treatment of approximation methods to implement conditional inequality path constraints for gradient-based numerical nonlinear programming solvers. This paper proposes two efficient methods to enforce conditional inequality path constraints in the optimal control problem formulation and compares and contrasts these approaches on representative airborne avoidance scenarios. The first approach is based on a minimum area enclosing superellipse function and the second is based on use of sigmoid functions. These proposed methods are not only robust, but also conservative, that is, their construction is such that the approximate feasible region is a subset of the true feasible region. Further, these methods admit analytically derived bounds for the over-estimation of the infeasible region with a demonstrated maximum error of no greater than 0.3% using the superellipse method, which is less than the resolution of typical sensors used to calculate aircraft position or altitude. However, the superellipse method is not practical in all cases to enforce conditional inequality path constraints that may arise in the nonlinear airborne collision avoidance problem. Therefore, this paper also highlights by example when the use of sigmoid functions are more appropriate.
<Keywords: Aviation; Collision; Inequality
χ: Heading angle (radians); Δxy: Horizontal separation distance (ft); Δz: Vertical separation distance (ft); δ: Overestimation error; ∈: Sigmoid exponential; γ: Flight path angle (radians); λ: Lagrange multiplierg Inequality constraintu Control; x: State trajectory; μ: Bank angle (radians); φ: Terminal cost function; ψ: Equality constraint; τ: Time transformation; g: Gravity constant ( ft/sec2); H: Hamiltonianh Horizontal constraint (ft); J: Performance measure; L: Cost function; N: Superellipse exponential; Nz: Normal acceleration; S: Sigmoid values Sigmoid stiffness; TCPA: Time to closest point of approach (CPA) (sec); V: Ground speed (ft/sec); v: Vertical constraint (ft)
Under the Federal Aviation Administration (FAA) Modernization and Reform Act of 2012, the United States Congress tasked the FAA to “provide for the safe integration of civil unmanned aircraft systems into the national airspace system” [faa_reform_act]. A means to meet this integration mandate is through the use of algorithms that autonomously generate optimal collision avoidance trajectories to satisfy current FAA regulations that mandate passing aircraft meet either a minimum horizontal or vertical separation distance. A number of works have looked at trajectory planning and optimization for air vehicles using optimal control problem formulations Raghunathan [1], Eele [2], Horn [3] and some, such as Geiger [4] have even demonstrated this method in flight on a small-size unmanned vehicle. However, a potential limitation of this method is enforcing conditional inequality constraints such as maintaining either a minimum horizontal or vertical separation distance from an approaching aircraft or complying with FAA right of way (ROW) rules. For example, according to FAR 91.113 if two aircraft are approaching nearly head on, then “each aircraft shall alter course to the right.” Optimal control problems are often solved using gradient based numerical nonlinear programming (NLP) solvers which require smooth differentiable constraints; however, conditional constraints are not always differentiable, and thus can cause gradient-based numerical solvers to fail. This paper proposes and analyzes two different methods to address the issue of non-differentiable conditional inequality path constraints. The first approach is based on a minimum area enclosing superellipse (MAES) function and the second is based on the use of sigmoid functions. Both of these approaches are differentiable, allowing the NLP solver to calculate gradients and find an optimal solution.
Standard methods for implementing conditional inequality constraints can be classified as indicator methods, including Big M Borrelli [5], Winston [6] and active set Hintermuller [7] methods, and mixed-norm methods Sadovsky [8]; however, these methods are not everywhere-differentiable, and therefore, they often cause gradientbased NLP solvers to fail to generate an optimal solution. For instance, Big M methods implement “either-or constraints” Winston [7] using a binary indicator variable along with a sufficiently large constraint variable (M); thus, constraints become non-differentiable with respect to the binary indicator variable. Similarly, active set methods use the conditional constraints to define sub-sets of feasible solutions and then optimize over each sub-set when it is indicated as the active set. However, these methods are not well suited for dynamic conditional constraints such as the time varying airborne collision avoidance problem since the continuous-time constraints implicitly define an uncountable number of feasible sub-sets, while discretizing the constraints introduces an implicit or explicit binary indicator variable equivalent to those in Big M methods [7]. In addition, mixed-norm methods typically formulate a set of conditional constraints as a single constraint involving the maximum of a set of norms from each conditional constraint Sadovsky [8]; thus, the constraint’s derivative at a point is a function of the derivative of the norm that obtains the maximum value at that point. Therefore, if the mixed set of norms do not have identical derivatives at points where the maximum norm changes from one norm to another in the set, the mixed-norm formulation will not be everywhere-differentiable. In the context of collision avoidance, Raghunathan [1] devised a novel approach for enforcing a conditional inequality constraint of maintaining either a minimum horizontal or vertical separation distance from an approaching aircraft; however, their approach did not address situations with more than two conditional constraints and required the introduction of an additional control variable appended to the objective function. An approach that is similar to the methods in this paper is known as artificial potential fields or functions, or APF. While APF methods are differentiable Ren [9], Paul [10] they do not truly enforce conditional inequality constraints. Instead, APF methods treat path constraints as “soft” obstacles and incorporate them as weighted penalties in the cost function which may result in generating infeasible trajectories [9]. However, the methods proposed in this paper provide conservative and differentiable approximations for indicator methods as well as mixed-norm methods, thus ensuring differentiability for the gradient-based NLP solver while maintaining feasibility for the optimal control problem.
The overview of this paper is as follows: Section 2 introduces and develops the MAES and sigmoid conditional constraint approximation methods. Sections 3 - 5 describe and then analyze the simulation results from the two example problems in this paper and Section 6 summarizes the results.
This section begins by introducing the first of the two example problems in this paper to properly motivate the development of the conditional constraint formulation methods presented herein. In the first example problem, the objective is for the ownship to minimize deviations from a 3D flight path corridor while maintaining either a horizontal separation distance (Δxy) of at least 2460 ft or a vertical separation distance (Δz) of at least 820 ft from an intruder aircraft where1:
 (1)
(1)
 (2)
(2)
Using logic ‘if statements’, this inequality constraint formulation appears algorithmically as:
for each collocation node i=1ton
if Δxy (i) > 2460
hsep(i)=1
end
if Δz(i)>820
vsep(i)=1
end
end
 (3)
(3)
This definition for the conditional inequality path constraint in equation (3) was evaluated using two different gradient-based NLP solvers, IPOPT and SNOPT; however, as expected, due to the non-differentiable conditional constraint caused by the logic ‘if statements’, both solvers failed to converge to a solution since they could not determine a gradient direction to search in order to find an extremal point. Therefore, an alternate approach is needed to enforce a conditional constraint without the use of logic ‘if statements’. The two approaches analyzed in this paper are (1) MAES and (2) sigmoid functions to approximate inequality path constraints for the optimal control problem. The next sections describe these two approaches.
Minimum area enclosing superellipse (MAES)
The equation for a superellipse appears as:
 (4)
(4)
where a and b represent the semi-major and semi-minor axes of the superellipse while N ≥ 2 is an even number Weisstein [11]. The equation for the area of a superellipse Farrell [12] appears as:
Area=4abc (N) (5)
where C(N) is a ratio of gamma functions of N defined as described by Farrell in 2013:
 (6)
(6)
Additionally, a superellipse that encloses a rectangle with length (2h) and width (2v) centered at the origin must intersect each of the 4 corners of the rectangle. That is, the minimum area enclosing superellipse must satisfy,
 (7)
(7)
Since N must always be an even number, all 4 constraint expressions in equation (7) are equivalent. Furthermore, since 4C(N) in equation (5) is not a function of a or b, the optimization problem to determine the semimajor and semi-minor axes values, a* and b* respectively, that minimize the area of an enclosing superellipse for any even N ≥ 2 reduces to:
Minimize ab
such that
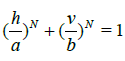 , where a,b ≥ 0
, where a,b ≥ 0
It is easy to verify that the values a*=21/N h and b*=21/Nv satisfy the first-order KKT and second-order sufficiency conditions for optimality. Therefore, the equation of the minimum area superellipse that encloses the minimum separation rectangle appears as:
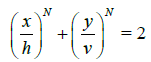 (8)
(8)
where h and v represent the minimum horizontal and vertical separation distance constraint, respectively.
Raising the exponential term, N, in equation (8) to higher-order even powers causes the superellipse to appear increasingly rectangular. Figure 1 graphically shows the results of increasing the exponential terms in equation (8). In this figure, the x-axis represents the horizontal separation constraint (Δxy) and the y-axis the vertical separation constraint (Δz). The red dashed lines depict the minimum separation distance of ± 2460 ft and ±820 ft in the horizontal (h) and vertical (v), respectively.
From Figure 1, in the limit as N→∞ the superellipse approaches the rectangular conditional constraints. Substituting x and y in equation (8) with Δxy and Δz, respectively, gives the superellipse equation as:
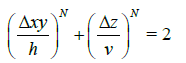 (9)
(9)
Note that,
 (10)
(10)
Furthermore Luenberger [13];
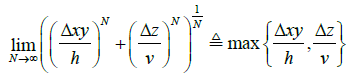 (11)
(11)
Therefore, if the mixed-norm is defined as described by Sadovsky in 2012:
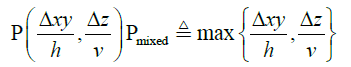 (12)
(12)
Then in the limit as N→∞ the superellipse equation (9) is equivalent to the dashed-red rectangle in Figure 1 given by the mixed-norm equation:
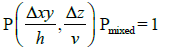 (13)
(13)
since,
 (14)
(14)
An advantage of using a MAES to approximate the conditional inequality constraint is that since the semi-major and semi-minor axes are defined as a*=21/N h and b*=21/Nv, respectively, the overestimation errors (δh and δv) for infeasible values of Δxy and Δz are bounded such that:
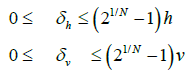 (15)
(15)
From equation (15), for given h and v the MAES overestimation error is strictly a function of N. For the example in this paper, the MAES method used a value of N=200, resulting in a maximum overestimation error of 0.3%, which is less than the typical resolution of an aircraft’s onboard sensors used to calculate position or altitude. Therefore, system designers should select the appropriate value of N based on sensor resolution. The minimum value of N necessary to guarantee the overestimation error is less than the sensor tolerance, Δs, is given by the smallest even number that satisfies the following relationships:
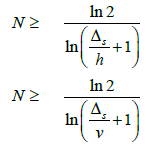 (16)
(16)
For example, if Δs=12 feet while h=2460 feet and v=820 feet, then:
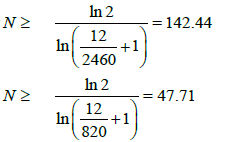 (17)
(17)
Therefore, N would be set to 144.
However, for large values of N, constraints involving the equation of the superellipse become computationally difficult to evaluate. This issue of constraint scaling is addressed by applying the natural log on equation (8) to generate the equivalent equation of the minimizing enclosing superellipse. The adapted equation appear as:
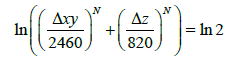 (18)
(18)
Therefore, the standard form of the inequality path constraint for the optimal control problem appears as:
 (19)
(19)
Equation (19) is the form of the MAES method used with equations (1) and (2) at each collocation node to solve the first example problem in this paper. However, it may be impractical to apply the MAES method to optimal control problems with multiple, compound (or nested) conditional inequality constraints, represented by the second example problem. To address this limitation, the next section develops differentiable approximations of indicator methods using a sigmoid function form of the conditional inequality path constraint.
Sigmoid function
Another approach to incorporate a conditional constraint is to use a sigmoid function approximation of a conditional indicator function. The earlier section described the problem that gradient-based NLP solvers have with non-differentiable conditional constraints. Like the MAES, sigmoid functions avoid this problem since they too are continuous and differentiable. Framing the development in the context of the first example problem, two unique sigmoid functions are defined to approximate the horizontal and vertical inequality path constraint indicator functions separately. The equations for the horizontal and vertical sigmoid functions, Sh and Sv, that approximate the inequality path constraint indicator functions appear as:
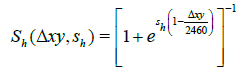 (20)
(20)
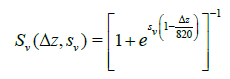 (21)
(21)
where Sh and Sv are user-defined positive stiffness factors for the smoothness and orientation of their respective sigmoid is as follows:
2 -2 cm - 2 cm [Desired Trigger Distance 2,460 ft] [Desired Trigger Distance: 820 ft.
Figure 2 shows the results of plotting equations (20) and (21) for varying values of positive Sh and Sv. Negative values of Sh and Sv merely reflect the image of the sigmoid function about the critical values (2460 and 820). From Figure 2, when Δxy=2460 or Δz=820 the value of the respective sigmoid equals 0.5. When Δxy < 2460 or Δz < 820 then the value of the respective sigmoid approaches zero. Likewise, when Δxy > 2460 or Δz > 820, the value of the respective sigmoid approaches unity. Therefore, the sigmoid functions define the inequality constraint indicator function approximations which appear as:
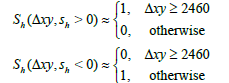 (22)
(22)
 (23)
(23)
This paper proposes and evaluates two different methods of using these sigmoid functions (a sum and then a product method) to approximate the conditional inequality path constraint. The first method involves summing the horizontal and vertical sigmoid values and the second involves taking the product of these two sigmoids. The following sections detail both methods where for convenience of notation, the exponential terms in equations (20) and (21) are defined as:
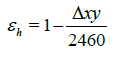 (24)
(24)
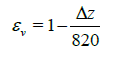 (25)
(25)
Sigmoid sum method: The sigmoid sum method is the more conservative of the two sigmoid methods. Given the conditional inequality path constraint of satisfying either a horizontal (h) or vertical (v) separation distance constraint, the sigmoid sum approximation of the conditional inequality path constraint appears as:
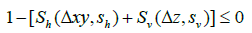 (26)
(26)
Where Sh and Sv are always positive. Therefore, if Δxy < 2460 and Δz < 820, then equation (26) is greater than zero. Thus, the sigmoid sum approximation method does not admit solutions that violate the true conditional inequality path constraint. However, if Δxy > 2460 while Δz < 820 or Δxy < 2460 while Δz > 820 then equation (26) may still be greater than zero, and thus, this method could fail to admit viable solutions that satisfy the true conditional inequality path constraint. The tolerance for when viable solutions are not admitted is a function of the user defined stiffness factor S. The relationships that determines if the sigmoid sum method will admit a viable solution are given by equations (27) - (29).
If Δxy ≥ 2460 and Δz ≥ 820 then,
 (27)
(27)
which implies that Sh (Δxy, Sh ) ≥ 0.5 and Sv (Δz, Sv) ≥ 0.5 so equation (26) is correctly satisfied.
If Δxy ≥ 2460 and Δz < 820 then,
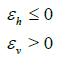 (28)
(28)
which implies that Sh(Δx, Sh) ≥ 0.5 and Sv (Δz, Sv) < 0.5 so equation (26) is correctly satisfied if and only if 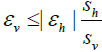 .
.
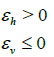 (29)
(29)
which implies that Sh(Δx, Sh) < 0.5 and Sv (Δz, Sv) ≥ 0.5 so equation (26) is correctly satisfied if and only if 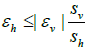 .
.
Equations (27) - (29) guarantee that the sigmoid sum method will only reject feasible solutions if one constraint is violated by more than the slack of the satisfied constraint times the ratio of the two stiffness factors. Furthermore, in the worst-case when Δz=0 then εv=1, so the minimum value of Δxy that will satisfy the sigmoid sum approximation of the conditional inequality constraint is given by the following relation:
if Δz=0, then
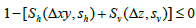 (30)
(30)

Similarly, in the worst-case when Δxy=0 then εh=1, so the minimum value of Δz that will satisfy the sigmoid sum approximation of the conditional inequality constraint is given by the following relation:
if Δxy=0, then
 (31)
(31)
Equations (30) - (31) indicate that the worst-case overestimation error can be very large. Additionally, the complexity of the sigmoid sum approximation surface indicates that NLP solvers could have difficulty estimating the gradient of the constraint (Figure 3). Therefore, a second sigmoid function method which reduces much of the overestimation error and improves differentiability is described next.
Sigmoid product method: Compared to the sigmoid sum method, the sigmoid product method allows greater precision in approximating conditional inequality constraints by reducing the maximum overestimation error that occurs when only one constraint is satisfied. Given the conditional inequality path constraint of satisfying a minimum horizontal (h) or vertical (v) separation distance constraint, the sigmoid product approximation of the conditional inequality path constraint appears as:
 (32)
(32)
where Sh and Sv are now both negative. The relationships given by equations (27) - (29) in the sigmoid sum method also determine if the sigmoid product method will admit a viable solution. However, for the sigmoid product method, if the horizontal constraint is satisfied but the vertical is not, that is, Δxy ≥ 2460 and Δz < 820 then equation (32) is correctly satisfied if:
 (33)
(33)
Similarly, if Δxy < 2460 and Δz ≥ 820, then equation (32) is correctly satisfied if:
 (34)
(34)
In the worst-case when Δz=0, then the minimum value of Δxy that will satisfy equation (32) is given by the following relationship:
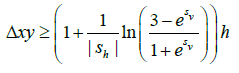 (35)
(35)
However, esv →0 as Sv→ -∞, so equation (35) can be approximated conservatively as:
 (36)
(36)
Likewise, when Δxy=0, then the minimum value of Δz that will satisfy equation (32) is given by the following relationship:
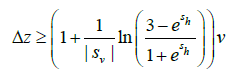 (37)
(37)
which can also be approximated conservatively as:
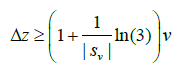 (38)
(38)
Therefore, the sigmoid product method bounds the overestimation errors (δh and δv) for infeasible values of Δxy and Δz such that::
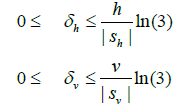 (39)
(39)
From equation (39), the maximum overestimation error is strictly a function of |Sh | and |Sv | . Due to the computational difficulty resulting from large exponential powers, with 40 fixed collocation nodes the largest absolute values for the sigmoid product parameters that were achieved were |Sh |= 240 and |Sv |= 80 . With these values the maximum overestimation error was 0.5% in the horizontal and 1.4% in the vertical. These values are much lower than the sigmoid sum method while comparable to the maximum overestimation error obtained in the MAES method. As with the MAES method, system designers can select the appropriate value of Sh and Sv based on sensor resolution. The minimum values of |Sh | and |Sv | necessary to guarantee that the overestimation error is less than the sensor tolerance, Δs, are given by the following relationships:
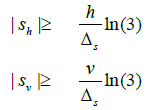 (40)
(40)
Since h=2460 and v=820 in the example problem, the minimum value of |Sv | needed to achieve a given tolerance will be 3 × greater than the minimum value of |Sv | needed to achieve the same tolerance.
Additionally, Figure 3 shows the normalized 3D constraint contour plots for the sigmoid sum and product methods for stiffness values of S=4 and 64 where S=Sh=Sv. The blue-colored area in the figure represents the feasible region where at least one constraint is satisfied and the redcolored area represents the infeasible region where neither constraint is satisfied. The thin black line on the constraint surface represents the true feasibility threshold and the thicker dashed line represents the conservative approximation to the feasibility threshold. For the sigmoid sum method the inequality constraint values, equation (26), range between ± 1 where negative values indicate at least one constraint is satisfied and values above 0.5 indicate neither constraint is satisfied. In the sigmoid product method the inequality constraint values, equation (32), range between -0.25 and 0.75 where negative values indicate at least one constraint is satisfied and values above 0.25 indicate neither constraint is satisfied. Therefore, to compare the two sigmoid methods the constraint contours (g*) in Figure 3 are normalized using:
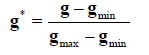 (41)
(41)
such that the constraint contour plots for both methods range between 0 and 1 where 0 indicates at least one constraint is satisfied and 1 indicates neither constraint is satisfied is shown as follows:
1 -2 cm -2 cm [Sigmoid Sum, S=4] [Sigmoid Sum, S=64] [Sigmoid Product, S=4] [Sigmoid Product, S=64]
During the optimization, the gradients of these constraint surfaces need to be calculated. Clearly, the sigmoid sum gradient is more complex due to the “stair-steps” and “sharp valleys” in the contour plots and thus is more difficult for the optimizer to establish the correct search direction. Subsequently, as shown in the analysis and confirmed by the results, the sigmoid product method is more efficient and allows higher stiffness values compared to the sigmoid sum method. Thus, the sigmoid product method was selected for use in the general case to resolve optimal control problems with multiple, compound (or nested) conditional inequality constraints. For problems of this type, it is necessary to use the generalized form of the sigmoid product constraint formulation given by:
 (42)
(42)
where K is the total number of conditional constraints being evaluated, gk ≤ max{gk} is a bounded constraint function such that hk - gk ≤ 0 if and only if condition k is satisfied and hk - gk > 0 if and only if the condition is not satisfied, and Sk< 0 is the stiffness factor. The overestimation error for each constraint in the generalized sigmoid product method is bounded similarly to the two-sigmoid case such that:
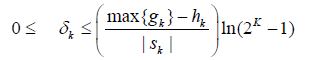 (43)
(43)
where δk is the overestimation error for values that violate conditional constraint k. Equation (43) also indicates system designers can select the appropriate value of Sk based on desired precision. The minimum value of |Sk | necessary to guarantee that the overestimation error is less than the precision tolerance, Δk, is given by the following relationships:
 (44)
(44)
Thus, equations (39) and (40) were used to determine the sigmoid product method parameters for the first example problem, while equations (43) and (44) were used to determine the sigmoid product method parameters for the second example problem.
The following section describes the example problems in this paper. The objective of the first example problem, as described earlier, is for the ownship to minimize deviations from a 3D flight path corridor while maintaining either a horizontal separation distance (Δxy) of at least 2460 ft or a vertical separation distance (Δz) of at least 820 ft from an intruder. The objective of the second example problem is identical to the first but requires the ownship to also adhere to FAA right of way (ROW) rules in addition to maintaining the intruder separation distances above. In this problem, the turn direction is conditioned on time and range from the intruder. The setup conditions for both example problems are identical. For both example problems, the collocation is performed at Legendre-Gauss-Radau quadrature points as described by Patterson in 2013.
Constraints
Equation (45) represents the dynamic constraints for the ownship that the optimization algorithm must satisfy when generating the optimal collision avoidance trajectory [musica:ddd]:
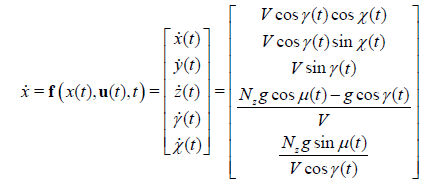 (45)
(45)
The states, x(t), in equation (45) consist of the cartesian directions (x,y,z), flight path angle (γ), and heading angle (χ). The controls, u(t), are bank angle (μ) for horizontal control and normal acceleration (Nz) for longitudinal or z-axis control where Nz is defined in the velocityaxis frame [musica:ddd]. The remaining variables in equation (45) are ground speed (V) and gravitational acceleration (g). An assumption for this model is that the aircraft’s flight control system will keep the vehicle speed constant throughout the avoidance maneuver.
In this problem the intruder aircraft maintains a constant speed of 300 ft/sec, a constant heading of 180° and a constant altitude of 6,000 feet. Although the optimal control problem formulation can easily accommodate multiple intruders and more complex and even stochastic models Smith [14] in this example problem we intentionally limited the problem to a single intruder and kept the intruder dynamic constraints simple in order to focus on the methodology for enforcing the conditional inequality path constraints. Thus, the intruder dynamic constraints appear as:
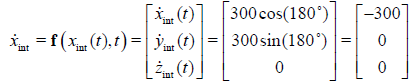 (46)
(46)
The equality boundary constraints are time initial (t0), time final (tf), ownship initial position (x0, y0, z0), and intruder initial position ( x0int, y0int, z0int) . These boundary constraints appear as:
 (47)
(47)
The inequality path constraint for the collision avoidance problem is the ownship must maintain at least 2460 feet separation distance horizontally or 820 feet vertically at all time from the intruder. To approximate this conditionally inequality constraint, the MAES, sigmoid sum, and sigmoid product methods are evaluated as described by equations (19), (26), and (32), respectively. In addition, the inequality control constraints, u(t), appear as:
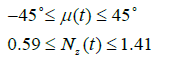 (48)
(48)
The symmetric control bounds on Nz(t) are reasonable maneuver limits for commercial transport or large remotely piloted aircraft. In addition, the upper bound on Nz(t) corresponds to the upper bound on μ(t) such that when both controls are at their maximum value the aircraft performs a level turn.
Performance measure
The performance measure for this problem is to minimize overall deviation distance (d) from the specified 3D flight path corridor centerline. In Figure 3 adapted from [wolfram: 3D_distance], x1 and x2 identify two consecutive waypoints, x(t) the current ownship position, and (d) the deviation distance such that [wolfram: 3D_distance]:
 (49)
(49)
where  (50)
(50)
r=0.55tw
Point Line Distance. Adapted from [wolfram: 3D_distance].
In this problem, x1 and x2 are defined in feet as:
x1 = [0, 2000,6000]
x2 = [25000, 2000,6000] (51)
Note that the ownship is trying to fly along the line through x1 and x2, but there is no time specified with either point.
In this section we first analyze the results of using the MAES to approximate the inequality path constraint and then examine the results of using the sigmoid methods for the first example problem. For comparison, in each case we used a global polynomial with 40 fixed collocation nodes and used IPOPT as the NLP solver. Simulations in this paper used Matlab version 2012 b on a laptop computer operating with OS X version 10.9 operating system and a 2.3 GHz Intel Core I 5 processor with 16 GB 1333 MHz DDR3 memory. The performance measure for this scenario was to minimize path deviation, as in equation (49). Since the minimum horizontal separation distance was 3× greater than the minimum vertical separation distance, intuitively the minimum deviation trajectory was for the ownship to intercept the 3D flight path corridor and change altitude only when required to meet the conditional separation constraint. The simulation results confirmed this intuition. The primary differences in these two approaches was the accuracy of the approximation and the time required for the optimizer to achieve a solution is as follows:
1 - 2 cm - 2 cm [Time 0 seconds] [Time 14.8 seconds] [Time 37.6 seconds] [Time 60 seconds]
To standardize the results we provided the NLP solver with the same conservative initial guess for each simulation run which consisted of the ownship flying level at the initial condition heading of 0 degrees.
The minimum path deviation trajectory for all three methods appeared similar. Although Figure 4 is a time-series quad chart of only the MAES simulation results, the minimum path deviation trajectories from the sigmoid methods appeared the same as the results in this figure. In this figure, the ownship is depicted in blue, the intruder in red, and the desired 3D flight path corridor in black. Both aircraft started the scenario at the same altitude of 6,000 feet MSL with the ownship 2,000 feet south (positive y-axis) of the 3D corridor while the intruder started and remained on the corridor.
As seen in panel (a) of Figure 4, at the start of the scenario the ownship began an immediate left turn to intercept the 3D flight path corridor and then continued on the corridor at the specified corridor altitude of 6,000 feet as shown in panel (b). In panel (c), the ownship then deviated from the corridor altitude by climbing only when required to meet the conditional separation inequality constraint. After satisfying this conditional constraint, the ownship then descended and maintained the desired 3D flight path corridor for the duration of the time horizon shown in panel (d).
MAES simulation results
Table 1 summarizes the effects of increasing the exponential terms in equation (19) on the normalized cost (J), number of NLP inequality constraint evaluations, CPU time in NLP evaluations, and the vertical and horizontal separation distances from the intruder at the closest point of approach (CPA).
| 2*MAES Order (N) |
2*Normalized Cost (J) | 2*# Inequality Constraint Evaluations | 2*CPU time in NLP Evaluations (sec) | Separation at CPA | |
|---|---|---|---|---|---|
| Vertical (ft) | Horizontal (ft) | ||||
| 2 | 1.666 | 130 | 26.41 | 1129 | 795 |
| 4 | 1.46 | 59 | 23.32 | 974 | 775 |
| 100 | 1.344 | 64 | 22.8 | 875 | 772 |
| 200 | 1.341 | 69 | 27.26 | 872 | 761 |
Table 1: IPOPT simulation results for MAES approximation of conditional inequality constraint.
The normalized cost (J) in Table 1 represents the ratio of the cost of intercepting the 33 corridor with an avoidance maneuver normalized by the cost of intercepting the 3D corridor without an avoidance maneuver. Note that these results are for 40 collocation nodes. While the number of nodes will affect the results, increasing the number of nodes will not necessarily cause the generated trajectory at the CPA to achieve the minimum feasible separation distances. In fact, due to the interaction between the aircraft dynamics and cost function, equations (45) and (49), the minimum vertical and horizontal separation distances at the CPA may overshoot the minimum feasible separation distances of the active constraint for any number of collocation nodes.
Figure 5 graphically displays the results for N=200. The blue asterisks in the plots show the horizontal (Δxy) and vertical (Δz) separation distances between the ownship and the intruder aircraft respectively at each collocation node for the 60 second time-horizon. The redline in each plot depicts the minimum horizontal (2460 ft) or vertical (820 ft) separation distance. Figure 5 shows that at approximately 12 seconds, the ownship began a climb so that as the horizontal separation decreased to below 2460 ft, at approximately 26 seconds, the ownship achieved the required vertical separation of at least 820 ft. In this plot, the ownship climbed above the minimum altitude of 820 ft and peaked at an altitude of approximately 870 ft. The results for both sigmoid methods appeared similar to the results in Figure 5.
Sigmoid simulation results
Sigmoid sum results: Table 2 summarizes the results of increasing the stiffness factors (Sh and Sv) in equation (26) on the cost (J), number of inequality constraint evaluations, CPU time in NLP evaluations, maximum vertical separation distance from the intruder, and the minimum horizontal separation distance from the intruder.
| 2*Stiffness factor ( Sh, Sv) | 2*Normalized Cost (J ) | 2*# Inequality Constraint Evaluations | 2*CPU time in NLP Evaluations (sec) | Separation at CPA | |
|---|---|---|---|---|---|
| Vertical (ft) | Horizontal (ft) | ||||
| (50, 50) | 1.656 | 583 | 228.70 | 1122 | 790 |
| (100, 100) | 1.458 | 1174 | 365.56 | 971 | 776 |
| (125, 125) | 1.423 | 1189 | 400.82 | 941 | 777 |
Table 2: IPOPT simulation results for sigmoid sum approximation of conditional inequality constraint.
Sigmoid product results: Table 3 summarizes the results for the sigmoid product method of increasing the stiffness factors (Sh and Sv) in equation (32) on the cost (J), number of inequality constraint evaluations, CPU time in NLP evaluations, maximum vertical separation distance from the intruder, and the minimum horizontal separation distance from the intruder.
| 2*Stiffness factor ( Sh, Sv ) | 2*Normalized Cost (J) | 2*# Inequality Constraint Evaluations | 2*CPU time in NLP Evaluations (sec) | Separation at CPA | |
|---|---|---|---|---|---|
| Vertical (ft) | Horizontal (ft) | ||||
| (180, 60) | 1.443 | 121 | 50.81 | 825 | 989 |
| (210, 70) | 1.422 | 128 | 52.9 | 824 | 968 |
| (240, 80) | 1.403 | 80 | 38.69 | 824 | 915 |
Table 3: IPOPT simulation results for sigmoid product approximation of conditional inequality constraint.
Sensor tolerance evaluation results
The sigmoid sum method had the largest computational time and was the most conservative of the three methods. Therefore, the following sensor tolerance evaluation focuses on the performance of the MAES and sigmoid product methods with parameters chosen to guarantee maximum overestimation errors less than a given sensor tolerance. For simplicity, this evaluation assumes the horizontal and vertical sensor tolerances are equal. From the previous example, for a sensor tolerance of ± 12 feet, the minimum value of N for the MAES method to guarantee the maximum overestimation error is less than the sensor tolerance are N=144. Similarly, from equation (40) for the sigmoid product method the minimum values of |Sv | and |Sv | required to guarantee the maximum overestimation error is less than the sensor tolerance are |Sv |= 76 and |Sv |= 76 . Table 4 shows the results for the MAES and sigmoid product methods with parameter values that guarantee the maximum overestimation error is less than sensor tolerances of 12, 25 and 50 feet [15-19].
| Sensor Tolerance (ft) |
Method | Normalized Cost (J) |
Constraint Activation times (sec) |
CPU time in NLP (sec) |
Separation at CPA | |
|---|---|---|---|---|---|---|
| Vertical (ft) | Horizontal (ft) | |||||
| 12 | MAES | 1.399 | t1 = 25.69 | 254.88 | 919 | 116 |
| N = 144 | t2 = 32.73 | |||||
| Sigmoid Product |
1.394 | t1 = 25.81 | 346.13 | 929 | 102 | |
| t2 = 32.86 | ||||||
| sh = -226 | ||||||
| sv = -76 | ||||||
| 25 | MAES | 1.406 | t1 = 25.81 | 236.54 | 918 | 110 |
| N = 70 | t2 = 32.86 | |||||
| Sigmoid Product |
1.396 | t1 = 25.81 | 285.51 | 931 | 102 | |
| t2 = 32.85 | ||||||
| sh = -109 | ||||||
| sv = -37 | ||||||
| 50 | MAES | 1.401 | t1 = 25.80 | 147.1 | 936 | 107 |
| N = 36 | t2 = 32.85 | |||||
| Sigmoid Product |
1.399 | t1 = 25.81 | 162.75 | 934 | 107 | |
| t2 = 32.86 | ||||||
| sh = -55 | ||||||
| sv = -19 | ||||||
Table 4: Comparison of methods for achieving error less than sensor tolerance.
The previous results in Sections 4.1 and 4.2 used only 40 collocation nodes and these nodes spanned the entire trajectory as a single “global” interpolating polynomial. However, to increase the fidelity of the solution especially near the constraint activation boundaries, the results in table are divided the trajectory into 20 equal-spaced segments with 10 collocation nodes per segment by Huntington in 2007. Although not reflected in the table, an alternate formulation applied an adaptive mesh refinement strategy by Patterson in 2013, which adaptively increased the number and placement of collocation nodes to achieve a user-defined level of accuracy. However, since the execution times for the adaptive node placement strategy varied significantly based on the number of mesh refinements, for standardization and comparison of results, a fixed number of collocation nodes was preferred for this analysis. Furthermore, due to the longer execution times of an adaptive node placement strategy, any eventual implementation of a real-time airborne collision avoidance algorithm would likely use fixed collocation nodes.
To better gauge the changes in the ownship trajectory as a function of the change in the sensor tolerance, the results in Table 4 replaced the column showing the number of inequality constraints evaluations in Tables 4 with a new column that showed the constraint activation times. As seen in Figure 5, the intersection of the red-dashed line and blue-asterisk indicate the constraint activation times. For the sensor tolerance evaluation, changes in the constraint activation times can provide additional insight into the sensitivity of the aircraft dynamics to the sensor tolerance. For instance, the performance measure (J) in this problem should force the optimal trajectory towards the “corner” of the constraint boundary where the horizontal and vertical constraints are active since in both MAES and sigmoid methods, these constraint corners are where the overestimation error is zero. This fact is particularly evident in Figure 1 where the formulation of the MAES optimization problem in equation (7) minimized the overestimation error at the corners of the rectangular constraint area.
In general the normalized cost (J) in Table 4 increased slightly as the predicted overestimation error increased. However, the constraint activation times remained consistent with the constant ground speed assumption, and the minimum separation distances at the CPA did not noticeably change as the sensor tolerance increased. These results indicate that the aircraft dynamics and trajectory optimization process were not sensitive to the range of sensor tolerances in the table. Since the overestimation error achieved its minimum value at the constraint corner, the optimizer forced the trajectory to intersect this corner as seen by the consistent constraint activation times. Even at a sensor tolerance of 50 feet, the ownship dynamic constraints were still what drove the optimal trajectory to start a climb away from the desired flight path in order to intersect the constraint corner; that is, the ownship climbed to reach an altitude of 820 feet above the intruder at the exact moment the horizontal separation distance decreased to less than 2460 feet. Likewise, after the two aircraft passed, the ownship then descended below 820 feet above the intruder at the exact moment when the horizontal separation distance again increased to greater than 2460. Thus, the trajectory was insensitive to sensor tolerances up to 50 feet. This was because the ownship’s dynamics forced the aircraft to climb to intersect the constraint corner rather than to avoid the worst-case overestimation region corresponding to sensor tolerances up to 50 feet. As a result, based on the intercept geometry of this example problem, the optimal trajectory should not change significantly until the sensor tolerance is significantly greater than the aircraft’s dynamic constraints required to intersect the constraint corner. For example, the earlier MAES results with N=2 correspond to sensor tolerances of greater than 330 feet which was reflected in the fact that at the CPA the altitude separation was approximately 360 feet greater than the minimum required separation distance. Therefore, based on the intercept geometry the aircraft dynamics may be more important in determining the precision of the approximation rather than the sensor tolerance since the optimal trajectory may remain unchanged for varying values of realistic sensor tolerances and scaling may not be required.
Nonetheless, Table 4 confirmed the methods presented in the paper and provides users a means to implement conditional inequality path constraints with a gradient-based numerical solver to the desired level of precision. Additionally, the results confirm that if the problem involves only two simple constraints, then the MAES method is the superior approximation method.
Unlike the previous example problem of satisfying a minimum horizontal or vertical separation distance where the MAES method performed well, an optimal control problem formulation may include multiple, compound (or nested) conditional constraints that do not lend themselves practically to the MAES formulation. An example of this type of complication is adhering to FAA right of way (ROW) rules, which state that if two aircraft are approaching nearly head on, then “each aircraft shall alter course to the right.” Since air traffic control procedures prefer horizontal over vertical maneuvers to maintain safe separation, in addition to implementing this conditional ROW constraint, this example problem also uses a new weighted cost function that separately penalizes ownship horizontal and vertical deviations from “each aircraft shall alter course to the right.” Since air traffic control procedures prefer horizontal over vertical maneuvers to maintain safe separation, in addition to implementing this conditional ROW constraint, this example problem also uses a new weighted cost function that separately penalizes ownship horizontal and vertical deviations from a desired 3D flight path corridor. This new cost function appears as,
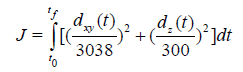 (52)
(52)
Where dxy(t) is the horizontal deviation from the 3D corridor centerline and dz(t) is the vertical deviation. The quadratic penalty in equation (52) is based on an assumed 3D corridor defined as ± 3038 feet (half a nautical mile) horizontally and ±300 feet vertically from centerline. Because this new cost function will likely cause the ownship to maneuver horizontally instead of vertically to maintain safe separation, the ownship will need to comply with the horizontal ROW constraint and alter course to the right since their approach will be nearly head on in this example problem.
Right of way formulation
In formulating the conditional ROW constraint, the sigmoid product method is used to implement a set of conditional logic ‘if statements.’ The feasibility region for the conditional ROW constraint is described by the following set of compounded logic OR conditions: If the separation distance between the ownship and intruder is greater than or equal to 2× the horizontal keep out radius of 2460 feet OR the time to CPA (TCPA) is greater than or equal to 30 seconds OR time from CPA is less than or equal to -5 seconds OR the relative azimuth angle (θ) between the ownship and the intruder is greater than or equal to zero (so the ownship will pass to the right of the intruder) then the solution is feasible; otherwise, the trajectory is not feasible. This inequality constraint formulation appears algorithmically as follows:
if 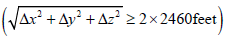
feasible
else if (TCPA ≤ -5 seconds)
feasible
else if ( TCPA 30 Seconds)
feasible
else if (θ 0)
feasible
else
infeasible
end
Each of the four conditional constraints in the ROW formulation are approximated using unique sigmoid functions. The range separation indicator function approximation at each point appears as:
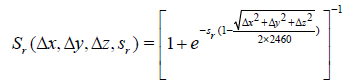 (53)
(53)
Thus, when  , the range indicator function approximation is active. By assuming a constant velocity and solving for the time that minimizes the instantaneous separation distance, the time to CPA (TCPA) appears as:
, the range indicator function approximation is active. By assuming a constant velocity and solving for the time that minimizes the instantaneous separation distance, the time to CPA (TCPA) appears as:
 (54)
(54)
where negative values indicate the two aircraft have passed or their velocity vectors are on non-convergent paths. Thus, the TCPA indicator function approximations appear as:
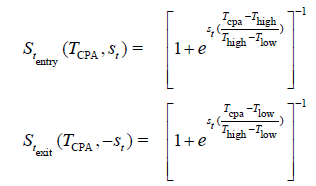 (55)
(55)
where Tlow=-5 seconds and Thigh=30 seconds, and when (TCPA> -5) OR ( TCPA< 30) the TCPA indicator function approximation is active. Finally, the turn direction constraint (Sθ) is formulated based on relative azimuth angle (θ) where,
 (56)
(56)
and is approximated at each instance in time using the following sigmoid function,
 (57)
(57)
where  . Thus, when ( >0) the “right turn” constraint approximated by equation (57) is satisfied. Therefore, based on equation (42) with K=4, the approximation of the ROW conditional inequality path constraint appears as:
. Thus, when ( >0) the “right turn” constraint approximated by equation (57) is satisfied. Therefore, based on equation (42) with K=4, the approximation of the ROW conditional inequality path constraint appears as:
 (58)
(58)
where  and
and  are defined in equations (53), (55), and (57), respectively.
are defined in equations (53), (55), and (57), respectively.
Simulation results
As described in Section 3, the setup for this second example problem is identical to the first problem; however, the cost function in equation (49) is now replaced by the weighted cost function in equation (52) is as follows:
1 -2 cm -2 cm [Time 0 seconds] [Time 18 seconds] [Time 45 seconds] [Time 60 seconds]
In addition, the ownship must now not only satisfy the conditional inequality path constraint in equation (19) formulated using the MAES method (N=200), but also satisfy the conditional inequality ROW constraint in equation (58) formulated using the sigmoid product method (St=Sr=Sθ=200). Like the sensor tolerance evaluation in the first example problem, this example divided the trajectory into 20 equal-spaced segments with 10 collocation nodes per segment. Figure 6 shows the simulation results. As in the first example problem, at the start of the scenario the ownship immediately maneuvered north (positive y axis) to minimize the path deviation from the 3D flight path corridor. However, due to the weighted cost function the ownship now maneuvered horizontally instead of vertically to keep out of the minimum separation distance from the intruder and correctly altered course to the right to comply with the conditional horizontal ROW constraint.
This example problem demonstrated that the sigmoid product method can effectively resolve multiple conditional constraints, to include constraints that are not naturally bounded (such as conditions that involve time or variables that are unrestricted in sign), and offers a robust alternative for problems where the MAES method is not suitable. Further, even with four conditional constraints as in this example problem, the error bounds for the sigmoid product method are valid. For example, based on equation (43) with St=Sr=200, the maximum overestimation error for the time and range conditional constraints was only 2.7%. Nevertheless, the use of this approach requires an understanding of the potential limitations. For instance, a well-known and often-stated critique of gradient-based NLP search methods is they produce local optimal solutions, which may or may not be global solutions. The formulation and testing of the ROW formulation highlighted the potential applicability of this critique in the context of airborne collision avoidance. For instance, given identical initial conditions, to enforce a “left turn” constraint required an initial trajectory guess to the left in order for the optimizer to locate the global vice the local optimal solution. A follow-on research effort explores potential methods such as those listed by Raghunathan in 2004, for appropriately choosing “smart” initial guesses for complex compounded conditional constraints. Another important consideration is the number of collocation nodes and stiffness of the sigmoid function. For instance, if the nodes are too sparse then the sigmoid appears as a binary switching function causing the NLP to fail since the conditional constraint approximation is no longer differentiable. For example, Figure 7 shows the NLP approximation of the conditional constraint (TCPA ≤ -5 seconds) for 200 fixed collocation nodes; panel (a) shows the results for (-St=200) where the NLP successfully converged and panel (b) shows the results for (-St=300) where the NLP failed to converge is as follows:
1 - 1 cm - 1 cm [NLP Converged] [NLP Failed to Converge]
Thus, the number and location of collocation nodes along with the sigmoid stiffness plays an important role in determining differentiability of the conditional constraint. Besides increasing collocation nodes and/ or decreasing the sigmoid stiffness factor, an additional remedy to this situation is to use an adaptive mesh refinement strategy by Patterson in 2013, as previously discussed which adaptively increases the number and placement of collocation nodes to help maintain differentiability of the conditional constraints approximated by the sigmoid functions. A final consideration when using this method is the potential for long convergence times. With 200 collocation nodes the NLP took 184.5 seconds to converge to a solution; however, in this paper the simulation algorithms were not necessarily optimized for speed but were coded for robust post-processing analysis. For real-time implementation these convergence times will need to be improved using techniques such as parallel processing or a more efficient programing language (Figure 8).
This paper motivated the application of conditional inequality path constraints in the nonlinear airborne collision avoidance optimal control problem. This paper then developed and demonstrated two different methods to enforce conditional inequality path constraints using numerical gradient-based solvers by approximating the mixednorm and indicator function classes of constraint formulations. In addition, this paper analytically derived the maximum overestimation error bounds associated with these different approximation methods and also provided designers a means to determine the minimum computational complexity needed to achieve desired results based on sensor performance. Using realistic collision avoidance scenarios, this paper demonstrated the performance of these methods and confirmed the validity of the error bounds. Furthermore, both the minimum area enclosing superellipse (MAES) and sigmoid product methods yielded good results; however, due to the geometric intuition and faster computation times the MAES method may be more advantageous for normalized and non-complex constraints. However, the MAES method is not well-suited if the conditional constraints are not continuous or if the constraints are compounded. In these cases, the sigmoid product method provides a robust means to satisfy conditional constraints and has good error bounds.
The authors would like to thank the United States Air Force Research Laboratory (AFRL/RQ) for sponsoring this research. In addition, the authors declare that there is no conflict of interest regarding the publication of this paper.