Journal of Geography & Natural Disasters
Open Access
ISSN: 2167-0587
ISSN: 2167-0587
Research Article - (2015) Volume 5, Issue 3
Climate Change is a hot issue in the world. Effect of climate change on yield of two varieties of boro rice has been assessed using the CERES Rice model of the DSSAT modeling system. The yield of BR3 and BR14 boro varieties for the years 2008, 2030, 2050 and 2070 have been simulated for 12 locations (districts) of Bangladesh, which were selected from among the major rice growing areas in different regions of Bangladesh. The CERES-Rice model uses a detailed set of crop specific genetic coefficients for predicting yield (BR3 and BR14) because “genetic coefficients” for these varieties are available in the DSSAT modeling system. Available data on soil and hydrologic characteristics of these locations, and typical crop management practice for boro rice were used in the simulations. The weather data required for the model (daily maximum and minimum temperatures, daily solar radiation and daily precipitation) were generated for the selected years and for the selected locations using the regional climate model PRECIS. The model predicted significant reduction in yield of both varieties of boro rice due to climate change; yield reductions of over 20% and 50% have been predicted for both rice varieties for the years 2050 and 2070, respectively. Increases in daily maximum and minimum temperatures have been found to be primarily responsible for reduction in yield. Increases in incoming solar radiation and atmospheric carbon-di-oxide concentration increases rice yield to some extent, but their effect is not significant compared to the negative effects of temperature. Variations in rainfall pattern over the growing period have also been found to affect rice yield. Increasing temperatures and solar radiation have been found to reduce the duration of physiological maturity of the rice varieties. Model results also suggest that in addition to reducing yield, climate change may also make rice yield more vulnerable to transplanting date, predicting significant reduction in yield as transplanting date is delayed, especially beyond 15 January. DSSAT modeling system could be a useful for assessing possible impacts of climate change and management practices on different varieties rice and other crops.
Keywords: Bangladesh; Climate change; Boro rice; Rice yield; CERES-Rice model
This article based on empirical nexus between three climate variables and rice yield has been estimated using aggregate level time series data. However, average aggregate data at the national level does not take into account potentially large differences between different crop producing regions or districts [1]. In reality, different areas are impacted heterogeneously by climate change [2,3]. Even then, the impact of climate change varies within and between agro-ecological regions of the same country [3,4]. This, therefore, warrants research using more disaggregated climate and rice yield data for a clearer understanding of the economic impact of climate change on rice production. Therefore, this work aims to estimate the economic impact of climate change on rice yields using cross-sectional time series data as well as disaggregated climate and rice yield data at the district level. These local levelestimates have the potential to reflect more accurately the relationship between the variables of interest [1,5]. This estimation will address research question two. In so doing, specific additional research questions are formulated to direct our analysis further:
• Is there any difference in climate variables across the regions or areas?
• How do the changes in temperature and rainfall affect the mean and variability of yield of three different rice varieties (Aus, Aman and Boro) transversely all seven climate zones?
• What will be the influence of future climate change setups on rice yields?
The organization of this part is as follows a brief overview of the literature, presents the methodology used for estimation purposes. Empirical findings are reported and discussed in this part.
A brief overview of the literature
One of the major determinants of fluctuations in crop yield is yearto- year changes in climatic variables [6,7]. There have been several studies measuring the effects of climate variables on crop productivity using either simulation models such as CERES-maize, CERESrice or EPIC [8,9] or regression models [4,10]. Mostly, two major methodologies were employed in these studies to assess the impact of climate on agriculture: the production function approach (also known as crop modelling or agronomic models) and the Ricardian approach [10].
The first approach, based on controlled experiments, simulates data on climate factors and crop yields in a laboratory-type setting. With careful control and randomized application of environmental conditions, this approach has its capability to forecast the potential climatic impacts on agricultural yields. However, this approach does not take into consideration farmers’ attitudes toward adaptation and thus results in an over estimation of negative impacts and an underestimation of positive effects [4,10].
In contrast, the Ricardian approach estimates the relationship between land values and agro-climatic factors by making use of cross-sectional data [10]. The main strength of this approach is that it captures farmers’ Mitigations that affect land values (net revenue or farm income). Consequently, the model has been successfully applied in many countries including the USA [10,11]; England and Wales [12]; Kenya [13]; Taiwan; South Africa [3]; Cameroon; China; and India and Brazil. However, the model, in its original form, cannot be applied to most developing countries because of the absence of efficient land markets. The major weakness of a Ricardian model lies in its in ability to incorporate omitted variables such as unobservable skills of farmers and quality of soil which are also known as time independent and location specific factors [14]. However, although variability in yield is found to be affected by climate variables in some studies [1,15,16] a Ricardian model is unable to assess the effect of climate change on yield variability. This has already led some economists to use a panel data approach to account for the problem of omitted variables by including district or regional dummies in the model [1,14,16-18]. Moreover, panel data provides more information and degrees of freedom, and can control individual heterogeneity. Furthermore, there are several other advantages in using a panel data approach such as increasing sample size considerably and it being better suited to study the dynamics of change by employing repeated cross-section observations [19].
Previous studies carried out internationally are based on the theoretical framework of Just and Pope’s (1978) stochastic production function approach. However, there have been, to the best of the researcher’s knowledge, no studies applying the panel data approach in Bangladesh. There are a few regional and national level studies on the impact of climate change or of droughts on rural livelihoods and crop agriculture using descriptive statistics and simulation models [20-22]. Therefore, there is a need to assess the effects of climate variables on mean rice yield and its variability in Bangladesh using a panel data approach. The analysis in this work is based on the stochastic production function approach introduced by Just and Pope.
This work will contribute to the literature in some important ways. First, there are few empirical studies about the impact of climate change on mean crop yield and its variability [1,16]. Second, earlier studies using panel data have used average temperature and rainfall as the two climate variables [1,16] Average temperature was constructed as an average of maximum temperature and minimum temperature. However, the inclusion of maximum and minimum temperature is only able to capture the differential impacts of day and night temperature [23]. Therefore, this study is the first that has employed both maximum and minimum temperature as temperature-related climate variables as well as rainfall in a panel data approach. Third, past studies using panel data evaluated the impact of climate change on a particular crop or a group of crops as a whole [1,14,16,18]. However, different varieties of a crop are impacted differently by climate change [13] which warrants crop-variety specific research. In this study, the impacts of climate variables are assessed for all three major rice crops in Bangladesh.
The methodology for estimation purposes
This section has used pooled cross-sectional time series data for the three major rice crops (Aus, Aman and Boro) for 13 out of 19 greater districts in Bangladesh. The selection of the districts was based on the availability of consistent data both on climate and rice yield. District level data on climate and rice yield for the 1972-2009 period are grouped into seven climatic sub-zones of Bangladesh as outlined by Rashid and discussed in Chapter Four (the time period for analysis matches available climate and rice production data). The summary statistics of data are described in Table 1. These data reveal that there is a correlation between higher mean values and higher standard deviation values. Both maximum and minimum temperature is higher during Aus rice period and lowest during Boro rice period. But absolute variability in temperature is higher for Boro rice. The variability in rainfall varies considerably among the three rice varieties which in large part correspond to their growing seasons.
| Rice Variety | Variables | Unit | Obs | Mean | Standard Deviation | Maximum | Minimum |
|---|---|---|---|---|---|---|---|
| Aus | Yield | (kg/acre) | 494 | 627.09 | 725.17 | 9714.6 | 48.35 |
| Maxt | (°C) | 494 | 32.43 | 0.99 | 35.4 | 29.32 | |
| Mint | (°C) | 494 | 24.83 | 0.70 | 26.3 | 18.4 | |
| Train | (mm) | 494 | 1597.61 | 627.58 | 4296 | 303 | |
| Aman | Yield | (kg/acre) | 494 | 621.73 | 180.66 | 1115.6 | 82.56 |
| Maxt | (°C) | 494 | 30.42 | 0.57 | 32.4 | 28.98 | |
| Mint | (°C) | 494 | 22.10 | 0.61 | 23.9 | 19.9 | |
| Train | (mm) | 494 | 1315.61 | 472.89 | 3647 | 347 | |
| Boro | Yield | (kg/acre) | 494 | 1073.68 | 308.88 | 4687.3 | 103.9 |
| Maxt | (°C) | 494 | 29.50 | 1.02 | 32.5 | 24.4 | |
| Mint | (°C) | 494 | 17.69 | 1.06 | 20.2 | 12.1 | |
| Train | (mm) | 494 | 478.27 | 280.09 | 70 | 1684 |
Source: Bangladesh Meteorological Department evaluated by Rashid
Table 1: Summary statistics on yields and climate variables.
Graphic statistics for district level climate variability
Descriptive statistics such as mean, standard deviation and CV are used to examine the district level variability for climate variables. Since the first objective of this chapter is primarily to examine the interdistrict or inter-region variations in climate, the relative variability expressed by the CV is a more appropriate measure than the standard error.
Panel unit roots and stationary
It is essential to investigate the presence of unit roots for each potential variable before we estimate the model either using the FGLS or MLE method. One important assumption of the Just and Pope model is that the variables under estimation are stationary [1]. Therefore, variables having the properties of I(1)must be differenced before panel estimation occurs. Otherwise, using anon-stationary data set directly might yield spurious results [15]. However, the time series properties of one variable comprising many regions in a panel data setting are hard to characterize [1]. This study uses the Fisher-type test as proposed in Maddala and Wu. The Fisher test obtains more precise results and achieves higher power compared to other tests such as LLC [14].
Empirical model specification and estimation method
In order to determine the effects of climate variables on the level of yield and its variability, the stochastic production function approach pioneered by Just and Pope is applied here. The fundamental concept underpinning this approach is that the production function can be decomposed into two segments: the first segment is linked to the mean output level while the second segment is associated with the variability of that output [16]. The general form of the Just and Pope production function is:
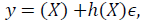
Where y is yield, X is a set of explanatory variables. The parameter estimation of (X) provides the average impact of the explanatory variables on yield while h(X) offers theireffect on the variability of yield [15]. Based on Saha et al. (1997) and Chen et al. [1] the following form of production function is estimated:
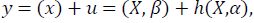
where, y is rice yield (Aus, Aman and Boro), X is a set of independent variables (e.g., temperature, rainfall, location and time period) and ε is the exogenous production shock with 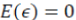 and
and 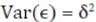 With this formulation, explanatory variables affect both mean and variability of rice yield because
With this formulation, explanatory variables affect both mean and variability of rice yield because 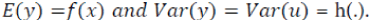 The parameter estimation of (.) gives the average effects of the independent variables on yield, while h(.) reveals the impacts of the covariates on the variability of yield. It is not worthy that a positive sign on any parameter of h(.) implies arise in that variable, i.e., an increase of the variability of yield. A negative sign on the same function indicates a decrease of the variability indicating that weather variables are risk declining inputs.
The parameter estimation of (.) gives the average effects of the independent variables on yield, while h(.) reveals the impacts of the covariates on the variability of yield. It is not worthy that a positive sign on any parameter of h(.) implies arise in that variable, i.e., an increase of the variability of yield. A negative sign on the same function indicates a decrease of the variability indicating that weather variables are risk declining inputs.
Three functional forms of production functions (Cobb-Douglas, quadratic and translog) are used for the estimation of the Just and Pope Production function [1,16,24] Because of the multiplicative interaction between the mean and variance, a translog functional form violates the Just and Pope postulates [24,25]. Therefore, Cobb-Douglas and linear quadratic forms are selected forthemean yield function estimation. These two forms are consistent with the Just and Pope postulates [16,25].
Mean function
The mean function is specified as: Cobb-Douglas form
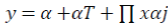
Linear- Quadratic Form
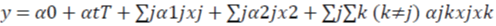
Where  are explanatory variables that include weather variables, Trepresents time trend and
are explanatory variables that include weather variables, Trepresents time trend and 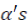 imply coefficients to be estimated. The justification of including the time trend is that it can capture technological progress over the period under consideration.
imply coefficients to be estimated. The justification of including the time trend is that it can capture technological progress over the period under consideration.
Variance function
Only the linear functional (CD) form is considered for the variability function because the variance function has a non-linear form and the inclusion of quadratic terms for explanatory variables makes the analysis more difficult. Following Just and Pope, Kumbhakar and Tveteras (2003) and Koundouri and Nauges (2005), the variability Function h(.) is modelled as a Cobb-Douglas form:
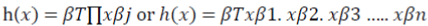
Logarithmic transformation of this function (Equation 5.6) produces the linear function as follows:
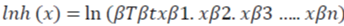
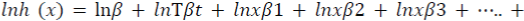
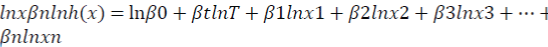
where 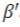 are parameters to be estimated.
are parameters to be estimated.
Fixed effects and random effects models are usually used for a panel model [26]. This study has used the fixed effects model purposely for two reasons. First, it allows region or district specific characteristics to be included which are one of the motivations of using a panel model. To take into account the regional differences in the mean yield function, regional dummies are included in the model. Second, the fixed effects model is appropriate in situations where there is a possibility of correlation between regressors and time-invariant distinctiveness [26]. In contrast, the random effects model necessitates the assumption of no correlation between unobserved time-invariant characteristics and the explanatory variables. Therefore, the fixed effects model is selected for this study and this selection is consistent with past studies [14,16] Both MLE and a three-step FGLS were prescribed in Just and Pope for estimating both functional forms. However, FGLS estimation has been employed in most quantitative studies, although MLE is more efficient and unbiased than FGLS for small samples. Given the large sample here, FGLS was used in this study as described in Judge et al, to estimate a form of fixed effects panel model for the above equations. Moreover, both FGLS and MLE were used in the preliminary analyses but FGLS was found to produce better results. This is another reason for the choice of FGLS as an estimation method. Furthermore, panel model estimation involving both cross-section and time series data may encounter the problems of heteroscedasticity and auto-co-relation [19,27]. These two problems are better addressed in FGLS since it assumes that panels are homoscedastic and there is no auto-correlation.
Descriptive statistics for climate variability at district level
In this section, climate variability is examined for each district and for each climatic zone. Table 2 sets out the inter-district climate variability. It is evident from the table that values of descriptive statistics for different climate variables vary considerably across and/or between the districts or regions. The districts of Rajshahi, Jessore and sathkhira have experienced highest mean maximum temperature whereas the relative variability is the highest for Rangpur and Sylhet.
| Greater district | Yearly mean maximum temperature | Yearly mean minimum temperature | Yearly average total rainfall | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | CV | Mean | Std | CV | Mean | Std | CV | |
| Dinajpur | 30.09 | 0.39 | 1.29 | 19.93 | 0.40 | 2.02 | 1958 | 449 | 22.96 |
| Rangpur | 29.60 | 0.61 | 2.05 | 20.00 | 0.70 | 3.49 | 2262 | 478 | 21.14 |
| Rajshahi | 31.11 | 0.38 | 1.21 | 20.54 | 0.44 | 2.15 | 1505 | 316 | 21.02 |
| Bogra | 30.67 | 0.40 | 1.31 | 20.86 | 0.35 | 1.70 | 1810 | 381 | 21.04 |
| Mymensingh | 29.92 | 0.37 | 1.24 | 20.74 | 0.46 | 2.22 | 2228 | 612 | 27.47 |
| Sylhet | 29.83 | 0.61 | 2.06 | 20.38 | 0.54 | 2.67 | 4071 | 612 | 15.04 |
| Dhaka | 30.65 | 0.54 | 1.77 | 21.64 | 0.44 | 2.04 | 2130 | 405 | 19.02 |
| Comilla | 30.20 | 0.43 | 1.42 | 20.93 | 0.33 | 1.57 | 2080 | 378 | 18.18 |
| Jessore | 31.55 | 0.50 | 1.58 | 20.85 | 0.30 | 1.44 | 1665 | 332 | 19.97 |
| Faridpur | 30.49 | 0.45 | 1.46 | 21.18 | 0.63 | 2.96 | 1872 | 347 | 18.53 |
| Sathkhira | 31.16 | 0.44 | 1.41 | 21.73 | 0.46 | 2.13 | 1842 | 358 | 19.46 |
| Barisal | 30.53 | 0.43 | 1.40 | 21.20 | 0.36 | 1.70 | 2116 | 363 | 17.17 |
| Chittagong | 30.35 | 0.54 | 1.79 | 21.68 | 0.44 | 2.01 | 2898 | 492 | 16.97 |
Source: calculation based on data collected from BMD (2010) by Sarker
Table 2: Inter-district climate variability for the 1972-2009 period.
In terms of mean minimum temperature, the districts of Faridpur, Sathkhira, Chittagong, Dhaka and Barisal have the maximum values while the Dinajpur district has the lowest value. From the view point of relative variability, the Rangpurdi strict experiences the highest variability. Other districts having high coefficients of variation include Rajshahi, Mymensingh, Sylhet, Dhaka, Faridpur, Khulna and Chittagong. Lowest variability in minimum temperature is found in the Jessore district. For rainfall data, the Sylhet district experiences highest yearly average total rainfall which is justabove 4000 mm while the average total rainfall is lowest in Jessore. In terms of rainfall variability, the districts ofMymensingh, Rajshahi, Rangpur, DinajpurJessore, Sathkhira&Bogra experience larger variations. This rubric picture becomes more comprehensive if these are analyzed in the context of climatic zones as illustrated in Table 3.
| Climatic zone | Yearly mean maximum temperature(°C) | Annual mean minimum temperature(°C) | Yearly average total rainfall(mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | CV | Mean | Std | CV | Mean | Std | CV | |
| Southeastern | 30.35 | 0.54 | 1.79 | 21.68 | 0.44 | 2.01 | 2898 | 492 | 16.97 |
| Northeastern | 29.83 | 0.61 | 2.06 | 20.38 | 0.54 | 2.67 | 4071 | 612 | 15.04 |
| Northern part of the north | 29.60 | 0.61 | 2.05 | 20.00 | 0.70 | 3.49 | 2262 | 478 | 21.14 |
| Northwestern | 30.38 | 0.32 | 1.06 | 20.40 | 0.36 | 1.76 | 1884 | 359 | 19.03 |
| Western | 31.11 | 0.38 | 1.21 | 20.54 | 0.44 | 2.15 | 1505 | 316 | 21.02 |
| Southwestern | 31.07 | 0.42 | 1.35 | 21.25 | 0.37 | 1.75 | 1793 | 285 | 15.90 |
| South central | 30.32 | 0.36 | 1.19 | 21.13 | 0.32 | 1.51 | 2138 | 359 | 16.77 |
Source: calculation based on data collected from BMD (2010) by Rashid
Table 3: Inter-climate zones variability in climate variables for the 1972-2009 period.
The data reveals that variability in climate variables changes across climate zones. Annual mean maximum temperature is highest for the western zone while it is lowest for the southern part of the south zone. The zones having the highest relative variability in maximum temperature include the southeastern and the southern part of the south. In terms of minimum temperature, the southeastern, northeastern, southern part of the south and south western zones experience the highest variability. From the view point of rain fall, the southwestern zone receives the lowest annual mean total rainfall. Variability in rainfall is also higher for the southwestern and the southern part of the south zones. Overall, there have been significant variations in climate variables across the districts and climate zones. However, the changes are more profound when seen in the context of climate zones. One important dimension of this finding is that the southwestern zone (i.e., Jessore and sathkhira district) has the highest maximum temperature and the lowest annual rainfall which has made the zone the most severely drought-prone area of Bangladesh. These findings are consistent with Islam and Neelim (2010). This is a strong basis for separate research focusing on the southwestern zone (i.e., the greater Jessore district), which is the focal point of Chapters 6 and 7.
The panel unit root test
The Fisher-type test is used to examine the stationarity properties of the variables under a panel model. There are two versions of the Fisher-type test: ADF and PP. This study finds identical results from these two versions and produces the results using ADF test. Moreover, another test, Harris-Tzavalis (HT), is also used to ensure the robustness of the results. The results are reported in Table 4.
| Rice variety | Variables | ADF test statistic(P-value) | Harris-Tzavalis test statistic | ||
|---|---|---|---|---|---|
| Without trend | With trend | Without trend | With trend | ||
| Aus | Yield | 87.00(0.000) | 115.76(0.000) | 0.67(0.000) | 0.64(0.000) |
| Maxt | 287.53(0.000) | 395.38(0.000) | 0.27(0.000) | -0.04(0.000) | |
| Mint | 237.48(0.000) | 255.32(0.000) | 0.28(0.000) | 0.16(0.000) | |
| Train | 530.41(0.000) | 481.65(0.000) | -0.11(0.000) | -0.15(0.000) | |
| Aman | Yield | 51.46(0.002) | 161.90(0.000) | 0.78(0.000) | 0.26(0.000) |
| Maxt | 217.89(0.000) | 401.00(0.000) | 0.46(0.000) | 0.12(0.000) | |
| Mint | 184.20(0.000) | 185.39(0.000) | 0.41(0.000) | 0.30(0.000) | |
| Train | 477.22(0.000) | 414.80(0.000) | -0.02(0.000) | -0.06(0.000) | |
| Boro | Yield | 119.53(0.000) | 186.35(0.000) | 0.32(0.000) | 0.01(0.000) |
| Maxt | 301.56(0.000) | 316.74(0.000) | 0.14(0.000) | 0.01(0.000) | |
| Mint | 199.68(0.000) | 269.67(0.000) | 0.38(0.000) | 0.17(0.000) | |
| Train | 499.39(0.000) | 459.50(0.000) | -0.11(0.000) | -0.15(0.000) | |
Notes: Hypothesis under ADF Test: Ho: All panels contain unit roots; Ha: At least one panel is stationary. Hypothesis under HT test: Ho: Panels contain unit roots; Ha: Panels are stationary. Source: Bangladesh Meteorological Department by sarker
Table 4: Panel unit root tests.
The estimated test statistics implies that rice yields and climate variables exhibit similar results under both with and without time trend. This suggests that the null hypothesis of unit roots (i.e., nonstationary) is rejected at the 1% level of significance for all variables in the table. This implies that all variables under the model are stationary. These results are consistent with McCarl et al and Kim and Pang [16]. Therefore, the three- stage FGLS can be applied to analyze the data without differencing.
The Quantitative model
Estimates of the linear Cobb-Douglas and linear quadratic functions form can yield and linear functions for yield variability are made using the FGLS estimation method. Regional dummies are included to the mean yield function but not to the variability function assuming different regions have different mean yields with almost identical variances across zones. Six regional dummies for seven climate zones are included to avoid dummy variable trap [19]. The estimated results for the three rice varieties are now presented.
Result for Aus rice
The regressors for the Aus rice model are jointly statistically significant because the overall Wald statistic of 984.36 under the linear functional form hasa P-value of 0.000 and that of the quadratic form is 788.01 has also a P-value of 0.000.
The detailed results are illustrated in Table 5. The sign and statistical significance of the estimated coefficients for the regressors in the mean yield function are found to be different between the linear and quadratic functional forms. Rainfall has a negative effect on mean Aus yield in the linear model but a positive effect in the quadratic model. It is statistically significant in the linear model, but not in the quadratic model. Both maximum and minimum temperatures are positively related to mean yield in the linear model while they have a negative effect in the quadratic model. However, both temperatures are statistically in significant in either model. No quadratic and interaction terms for climate variables in the quadratic model are statistically significant. All regional dummies in the linear model are individually statistically significant apart from the southwestern region. The statistically significant regions are the southeastern, northeastern, southern part of the south. Therefore, most of the regional dummies are statistically significant in both models. The trend is positively related to the mean yield and statistically significant in both models.
| Variables | Linear Model(Cobb- Douglas) | QuadraticModel | ||
|---|---|---|---|---|
| Coefficients | P-value | Coefficients | P-value | |
| Meanyield | ||||
| Trend | 0.019*** | 0.000 | 0.195*** | 0.000 |
| Tmax | 1.150 | 0.404 | -392.280* | 0.099 |
| Tmin | 0.167 | 0.875 | -37.331 | 0.881 |
| R | -0.246** | 0.030 | 1.478 | 0.936 |
| T2max | 46.631 | 0.175 | ||
| T2min | -8.303 | 0.424 | ||
| R2 | -0.021 | 0.944 | ||
| Tmax*Tmin | 21.010 | 0.670 | ||
| Tmax*R | -2.603 | 0.593 | ||
| Tmin*R | 2.342 | 0.670 | ||
| South-eastern | 0.564*** | 0.000 | 0.527*** | 0.000 |
| North-eastern | 0.447*** | 0.000 | 0.347* | 0.081 |
| Northern part of thenorth | 0.355*** | 0.000 | 0.357*** | 0.000 |
| Northwestern | 0.339*** | 0.000 | 0.334*** | 0.000 |
| Western | 0.234** | 0.040 | 0.106 | 0.387 |
| South-western | 0.033 | 0.666 | -0.010 | 0.894 |
| South central (omitted to avoid dummyvariabletrap) | ||||
| Constant | 35.815*** | 0.000 | 703.142 | 0.266 |
| Yield variability | ||||
| Trend | 0.007*** | 0.000 | 0.006*** | 0.000 |
| Tmax | 0.720*** | 0.000 | 0.691*** | 0.000 |
| Tmin | -0.658*** | 0.000 | -0.649*** | 0.000 |
| R | -0.008 | 0.446 | -0.007 | 0.496 |
| Constant | -9.849*** | 0.000 | -9.796*** | 0.000 |
| Model Summary | ||||
| Log likelihood | 739.56 | 686.17 | ||
| Waldchi-square | 984.36 | 788.01 | ||
| Prob>chi-square | 0.00 | 0.00 | ||
| AIC | -1469.12 | -1362.34 | ||
| BIC | -1448.10 | -1341.32 | ||
Note: ***, ** and * represent levels of significance at 1%, 5% and 10% respectively estimated by Rashid Calculated by Rashid
Table 5: Estimation results for Aus-rice.
For the yield variability function, the estimated coefficients show that increases in minimum temperature diminishes the variability of Aus rice yield. That is, minimum temperature is risk reducing whereas maximum temperature and total seasonal rainfall are risk increasing. However, only maximum temperature is individually statistically significant in the yield variability function. The trend variable is also statistically significant. This implies that crop yields increase over time due to technological progress such as improved irrigation coverage, expansion of HYVs and increased use of fertilizer.
These results are also in line with the findings of Anderson and Hazell [7], Isik and Devadoss, and Kim and Pang [16].
Results for Aman rice
The impact of climate change on Aman rice yield is reported in Table 6. The Wald statistics have a P-value of 0.000 both for the linear and quadratic models. This implies that the regressors under both models are statistically significant. The values of the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) were used to select the better functional form. The linear model is marginally better because it has a higher negative value.
| Variables | Linear Model(Cobb- Douglas) | Quadratic Model | ||
|---|---|---|---|---|
| Coefficients | P-value | Coefficients | P-value | |
| Mean yield | ||||
| Trend | 0.016*** | 0.000 | 0.015*** | 0.000 |
| Tmax | 4.054*** | 0.000 | -134.129*** | 0.011 |
| Tmin | -1.586*** | 0.000 | 113.628** | 0.057 |
| R | 0.018 | 0.624 | 6.614 | 0.229 |
| T2max | 20.334 | 0.110 | ||
| T2min | -19.145** | 0.028 | ||
| R2 | 0.019 | 0.759 | ||
| Tmax*Tmin | 2.696 | 0.868 | ||
| Tmax*R | -1.246 | 0.433 | ||
| Tmin*R | -0.841 | 0.443 | ||
| Southeastern | 0.374*** | 0.000 | 0.381*** | 0.000 |
| Northeastern | 0.021 | 0.616 | 0.001 | 0.984 |
| Northern part of thenorth | 0.220*** | 0.000 | 0.212*** | 0.000 |
| Northwestern | 0.099*** | 0.001 | 0.099*** | 0.001 |
| Western | 0.046 | 0.226 | 0.046 | 0.224 |
| Southwestern | -0.091*** | 0.001 | -0.091*** | 0.001 |
| South central (omitted to avoiddummyvariabletrap) | ||||
| Constant | -34.014*** | 0.000 | (omitted) | (omitted) |
| Yieldvariability | ||||
| Trend | 0.005*** | 0.000 | 0.005*** | 0.000 |
| Tmax | 1.151*** | 0.000 | 1.147*** | 0.000 |
| Tmin | -0.581*** | 0.000 | -0.580*** | 0.000 |
| R | 0.039*** | 0.000 | 0.039*** | 0.000 |
| Constant | -8.623*** | 0.000 | -8.615*** | 0.000 |
| Modelsummary | ||||
| Loglikelihood | 922.41 | 909.30 | ||
| Waldchi-square | 1495.62 | 1417.29 | ||
| Prob>chi-square | 0.00 | 0.00 | ||
| AIC | -1834.82 | -1808.60 | ||
| BIC | -1813.81 | -1787.59 | ||
Note: ***, ** and * represent levels of significance at 1%, 5% and 10% respectively estimated by Rashid
Table 6: Estimation results for Aman-rice.
The sign and level of significance for the impacts of climate variables for Aman rice differ between the linear and quadratic models. Maximum temperature has a positive impact on mean yields in the linear model and a negative effect in the quadratic model. Minimum temperature has a negative effect on rice yield in the linear model while a positive impact in the quadratic model. Finally, rainfall has a positive impact on rice yield though the effect is not statistically significant in either functional form. In the quadratic model, the quadratic term for minimum temperature is statistically significant with a negative effect on rice yield. The other two quadratic terms have positive impact but with no statistical significance. None of the three interaction terms are statistically significant but the interaction between maximum and minimum temperature has a positive effect on rice yield while the other two interaction terms have a negative impact.
All of the regional dummies are statistically significant in both models aside from the northeastern and western zones. Moreover, most of the significant regions have positive impact on yield except the southwestern which has a negative effect.
For the yield variability function, the effects of maximum temperature and rainfall on rice yield variability are positive and statistically significant. The impact of minimum temperature on rice yield is negative with statistical significance. This implies that minimum temperature is risk decreasing while maximum temperature and rainfall are risk increasing. Finally, the trend variable has a positive impact on both rice yield and variability in both models.
Results for Boro rice
Unlike Aman, Boro is an entirely irrigated rice crop. The impact of climate change on the mean and variability of Boro rice yield are illustrated in Table 7. The P-values of the Wald statistic confirm that both functional forms have overall statistical significance. However, the values of AIC and BIC make the linear model more significant.
| Variables | Linear Model(Cobb-Douglas) | Quadratic Model | ||
|---|---|---|---|---|
| Coefficients | P-value | Coefficients | P-value | |
| Mean yield | ||||
| Trend | 0.013*** | 0.000 | 0.013*** | 0.000 |
| Tmax | -0.036 | 0.949 | -71.304 | 0.139 |
| Tmin | 1.416*** | 0.000 | 6.631 | 0.828 |
| R | -0.018 | 0.584 | -1.613 | 0.597 |
| T2 max | 12.330 | 0.130 | ||
| T2 min | 0.209 | 0.918 | ||
| R2 | -0.045 | 0.298 | ||
| Tmax*Tmin | -3.734 | 0.662 | ||
| Tmax*R | -0.276 | 0.782 | ||
| Tmin*R | 1.067* | 0.070 | ||
| Southeastern | -0.114** | 0.040 | -0.139*** | 0.018 |
| Northeastern | -0.326*** | 0.000 | -0.280*** | 0.000 |
| Northern part of the north | 0.009 | 0.886 | -0.015 | 0.828 |
| Northwestern | 0.133*** | 0.005 | 0.125*** | 0.011 |
| Western | 0.063 | 0.303 | 0.051 | 0.421 |
| Southwestern | -0.007 | 0.846 | -0.011 | 0.786 |
| South central (omitted to avoid dummy variable trap) | ||||
| Constant | 3.109* | 0.094 | 121.082 | 0.175 |
| Yield variability | ||||
| Trend | 0.004*** | 0.000 | 0.003*** | 0.000 |
| Tmax | -0.007 | 0.869 | -0.006 | 0.904 |
| Tmin | 0.315*** | 0.000 | 0.315 | 0.000*** |
| R | -0.038*** | 0.000 | -0.037 | 0.000*** |
| Constant | 3.220*** | 0.000 | 3.216 | 0.000*** |
| Model summary | ||||
| Log likelihood | 1100.58 | -1063.44 | ||
| Waldchi-square | 532.95 | 460.23 | ||
| Prob>chi-square | 0.00 | 0.00 | ||
| AIC | -2193.16 | -2118.87 | ||
| BIC | -2176.35 | -2102.06 | ||
Note: ***, ** and * represent levels of significance at 1%, 5% and 10% respectively estimated by Rashid
Source: Bangladesh Meteorological Department
Table 7: Estimation results for Boro-rice.
The effects of climate variables on the mean and variability of rice yields differ between the linear and the quadratic models. The effect of minimum temperature on mean rice yield in the linear model is positive and statistically significant. The other statistically significant climate variable is the interaction term for minimum temperature and rainfall in the quadratic model. The remaining coefficients on the climate variables are not statistically significant in either model. Nevertheless, maximum temperature and rainfall have negative impacts on mean rice yield in both models. Of the regional dummies, the southeastern, northeastern and northwestern are statistically significant. However, the southeastern and northeastern have positive effects whilst the southwestern has a negative impact on mean rice yield.
For the yield variability function, the effects of minimum temperature and seasonal total rainfall on rice yield variability are statistically significant. However, the effect of minimum temperature is positive while that of rainfall is negative. This indicates that the minimum temperature is risk increasing while rainfall is risk decreasing in production.
Though the effects of maximum temperature on yield variability are not statistically significant, they have a negative effect. This implies that the maximum temperature is risk decreasing.
Climate elasticities of rice yields
Since the quadratic models have both quadratic and interaction terms, it is not possible to compare the signs and extent of the estimated coefficients in that model to those of the linear model. The estimation of elasticities is used to assess and compare the effects of climate variables both in the linear Cobb-Douglas and quadratic functional models. The elasticities are calculated at the mean values of the explanatory variables. The coefficients for climate variables such as maximum temperature, minimum temperature and rainfall can be translated into elasticities by multiplying the average climate variable and dividing by average yield [1]. These elasticities are reported in Table 8. The estimated elasticities are different between the linear and quadratic models for mean yield while the values for elasticities are slightly different in the yield variability function.
| Yield function | Climate variables | Rice variety | Linear Cobb-Douglas Model | Quadratic Model |
|---|---|---|---|---|
| Mean Yield | Maximum temperature | Aus | 0.0598 | -20.2934 |
| Aman | 0.1984 | -6.5645 | ||
| Boro | -0.0010 | -1.9598 | ||
| Minimum temperature | Aus | 0.0066 | -1.4788 | |
| Aman | -0.0564 | 4.0406 | ||
| Boro | 0.0233 | 0.1093 | ||
| Rainfall | Aus | -0.6265 | 3.7657 | |
| Aman | 0.0372 | 13.9959 | ||
| Boro | -0.0080 | -0.7187 | ||
| Yield Variability | Maximum temperature | Aus | 0.0372 | 0.0358 |
| Aman | 0.0563 | 0.0562 | ||
| Boro | -0.0002 | -0.0002 | ||
| Minimum temperature | Aus | -0.0260 | -0.0257 | |
| Aman | -0.0206 | -0.0206 | ||
| Boro | 0.0052 | 0.0052 | ||
| Rainfall | Aus | -0.0189 | -0.0188 | |
| Aman | 0.0829 | 0.0833 | ||
| Boro | -0.0168 | -0.7187 |
Source: Calculated by sarker, Bangladesh Meteorological Department
Table 8: Elasticities of climate variables.
The elasticities of the maximum temperature vary from-0.0010 to 0.1984 in the mean yield function for the three varieties of rice and -0.0002 to 0.0563 in the variance functions. Since these values are less than unity, the response of mean yields and variability of all three rice varieties to the changes in the maximum temperature are, therefore, inelastic. An increase in maximum temperature level usually decreases the mean and variance of Boro rice yield while it increases the mean and variability of Aus and Aman rice. Moreover, the estimated elasticities’ range is from -1.9598 to -20.2934 in the quadratic model implying mean yield changes to maximum temperature is elastic. This leads to the conclusion that the maximum temperature is yield decreasing for all rice varieties in the quadratic model. Furthermore, the estimated elasticities of maximum temperature are higher for Aman and Aus than that of Boro in both the mean yield and yield variability functions.
The estimated elasticities of the minimum temperature range from -1.4788 to 4.0406 in the mean yield functions while the range is between-0.0260 and 0.0052 in the yield variability functions. The estimated elasticities of minimum temperature for mean yields in the linear function are less than unity and thus in elastic for Aus, Aman and Boro. The elasticity for mean yield for Boro rice in the quadratic model is also in elastic. However, the estimated elasticities for the mean yields of Aus and Aman are greater than 1 in the quadratic model and thus elastic. The response of yield variability of all three rice yields to changes in minimum temperature is inelastic. An increase in minimum temperature reduces the variability of Aus and Aman rice yields, while it increases the variability of Boro rice yield.
The estimated elasticities of rainfall vary from-0.6265 to 13.9959 in the mean yield functions and -0.7187 to 0.0833 in the yield variability functions. Thus, the response of mean yields of Aus, Aman and Boro to changes in rainfall is mixed. More precisely, the mean yields for Aus and Aman to changes in rainfall are inelastic in the linear model, but elastic in the quadratic model. However, the mean yield for Boro is inelastic in both linear and quadratic models. The estimated elasticities are less than 1 in the yield variability function which makes the variance of the three rice yields to changes in rainfall inelastic. The signs of the elasticities imply that rainfall is risk increasing for Aman rice whilst it is risk decreasing for Aus and Boro yields.
Effects of future climate change
The elasticity estimates are now used in order to estimate the impacts of future climate change scenarios on rice yield and its variability. In so doing, a few climate change scenarios are modelled, based on scenarios from the Ministry of Environment and Forest [28]. This is applied to the growing periods of the three rice varieties and is shown in Tables 9 to 11. The changes in rice yields for each climate scenario are measured using the percentage changes in maximum temperature, minimum temperature and rainfall together with the elasticity estimates from Table 8. The percentage changes in mean Aus yield and variance for the years 2030, 2050 and 2100 are presented in Table 9.
| Changes in climate conditions | Changes in Aus rice yield | ||||||
|---|---|---|---|---|---|---|---|
| Year | Maximum temperature | Minimum temperature | Rainfall | Mean | Variability | ||
| LC | LQ | LC | LQ | ||||
| 2030 | 0.3 | 1.18 | 4.1 | -0.074 | -24.82 | -0.094 | -0.093 |
| 2050 | 0.2 | 1.24 | 2.3 | -0.020 | -19.35 | -0.109 | -0.109 |
| 2100 | -1.6 | -0.74 | 6.7 | -0.577 | +106.05 | -0.114 | -0.107 |
Note: LC = linear Cobb-Douglas and LQ = linear quadratic
Source: Calculated by sarker, collected data from Bangladesh Meteorological Department
Table 9: Change in mean Aus yield and yield variability (percentage).
| Changes in climate conditions | Changes in Aman rice yield | ||||||
|---|---|---|---|---|---|---|---|
| Year | Maximum temperature | Minimum temperature | Rainfall | Mean | Variability | ||
| LC | LQ | LC | LQ | ||||
| 2030 | 1.3 | 1.78 | 3.8 | +0.404 | +8.54 | +0.099 | +0.098 |
| 2050 | 0.89 | 1.65 | 3.0 | +0.168 | +14.16 | +0.030 | +0.030 |
| 2100 | 1.54 | 1.98 | 12 | +0.533 | +15.74 | +1.76 | +1.76 |
Note: LC = linear Cobb-Douglas and LQ = linear quadratic
Source: Calculated by sarker, collected data from Bangladesh Meteorological Department
Table 10: Change in mean Aman yield and yield variability (percentage).
| Changes in climate conditions | Changes in Boro rice yield | ||||||
|---|---|---|---|---|---|---|---|
| Year | Maximum temperature | Minimum temperature | Rainfall | Mean | Variability | ||
| LC | LQ | LC | LQ | ||||
| 2030 | 0.02 | 0.65 | -8.7 | +0.100 | +1.58 | +0.04 | +1.33 |
| 2050 | 0.07 | 0.59 | -4.7 | +0.085 | +0.60 | +0.03 | +0.72 |
| 2100 | -0.009 | 1.80 | -10 | +0.254 | +2.68 | +0.08 | +1.56 |
Note: LC = linear Cobb-Douglas and LQ = linear quadratic
Source: Calculated by sarker, collected data from Bangladesh Meteorological Department
Table 11: Change in mean Boro yield and yield variability (percentage).
These results imply that the mean yields for Aus rice would fall, to some extent, in response to the projected climate changes for the years 2030 and 2050. However, the percentage decrease in mean yield under the quadratic model is far greater than that of the linear model. Furthermore, mean yield for 2100 decreases in the linear model where a sit increases in the quadratic model. The variability of Aus rice yield would decline by almost the same percentage in both functional forms over the three periods. Most importantly, the decrease in variability increases overtime.
The percentage changes in mean Aman yield and variance for 2030, 2050 and 2100 are presented in Table 10. These data indicate that all three scenarios of climate change would result in an increase in mean rice yield in both the linear and quadratic models. However, mean yield increase in the quadratic model is well above the value for the linear model. On the other hand, future climate changes would increase Aman yield variability over the years and the variations are profound when comparing 2030 and 2100. However, the percentage variability changes are very similar in both models.
The change in Boro rice yield would increase for all the three time periods and in both models as shown in Table 11. For example, the percentage increases in mean yield are 0.10% and 1.58% for the linear and quadratic models respectively for 2030 while the values are 0.25% and 2.68% for 2100, respectively. The variance of Boroyield would increase over the three periods. It is not worthy that mean yield and variability for rice yields however expand at decreasing rates. However, future climate change would have adverse impacts on rice yield variability which might result in production fluctuations and spiral price changes for rice [16].
Climate change will impact upon the mean and variability of rice crop yields [1,16]. This work was to assess climate variability at the district and climate zone levels. Descriptive statistics reveal that there are significant variations in climate variables across the districts and climate zones during the 1972-2009 periods. However, the changes are more profound when district level data are aggregated to climate zone. One important dimension of the findings is that the Southwestern zone (i.e., the greater jessore and Sathkhira districts) has the highest maximum temperature and the lowest annual rainfall which makes the zone the most severe drought-prone area of Bangladesh. These findings are also consistent with other studies [29].
The second, and main, research objective of this work was to evaluate the effects of climate changes on the yield and variability of three main rice varieties using disaggregated data. The Just-Pope production function was used as the theoretical frame work and a balanced panel data model was utilized to achieve this objective. The results reveal that the impacts of climate variables vary among the three rice varieties. Maximum temperature is positively related to Aus and Aman mean rice yield in the linear model while the relationship is negative in the quadratic model. The elasticity values under the variance function imply that maximum temperature is risk increasing for Aus and Aman rice while risk decreasing for Boro rice production. However, the impacts of minimum temperature on yield variability are different. An increase in minimum temperature is likely to decrease the yield variability for Aus and Aman rice production while the yield variability for Boro rice is increased. Therefore, minimum temperature is risk increasing for Boro rice and risk decreasing for Aus and Aman varieties. Finally, the impacts of rainfall on yield variability are positive for Aman rice and negative for Aus and Boro rice. This confirms that rainfall is risk increasing for Aman rice while risk decreasing for Aus and Aman rice.
These results provide further evidence of the potential productivity losses which will occur with changes in climate. Moreover, most of the regional dummy variables are statistically significant with differential impacts on rice yield. This proves that different climate zones are impacted differently by climate change. Therefore, the severity of climate change effects on rice yields varies among the climate zones. This cautions against national or state level adaptation policies which maybe in effective and consequently suggests region specific or climate zone specific adaptation policies. This then warrants the need for more location-focused research on climate change and agricultural production to devise local or micro level adaptation policies for reducing yield variability, ensuring food security and all aviating rural poverty in the presence of climate change.
Three time scenarios (2030, 2050 and 2100) were developed to model potential climate changes on rice yield and its variability. The changes in rice yield for each of these scenarios were measured using the percentage changes in maximum temperature, minimum temperature and rainfall in an aggregate form. The results reveal that future climate change is expected to increase the variability of rice yield for Aman and Boro varieties. However, the variability will be higher for rain-fed Aman rice compared to the irrigated Boro rice crops.
Finally, a major caveat is that although the panel data model is an improvement overtime series and cross-sectional data; the model does not always provide a cure-all for the econometrician’s problems [19]. For example, how individual farmers are affected by climate change is not discernable from the panel data model results. It has been found elsewhere that the impact of climate change is more profound at the farm level. Data from a survey of farmers thus can indicate the impact of climate change and climate related extreme events more explicitly.