Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2013) Volume 2, Issue 1
Engineering improvements, technology enhancements and advanced operations have an important role to play in reducing aviation fuel consumption and environmental emissions. Currently several organizations worldwide are focusing their efforts towards large collaborative projects whose main objective is to identify the best technologies or routes to reduce the environmental impact and fuel efficiency of aircraft operations. The paper describes the capability of a multi-disciplinary optimization framework named GATAC (Green Aircraft Trajectories under ATM Constrains) developed as part of the Clean Sky project to identify the potential cleaner and quieter aircraft trajectories.
The main objective of the framework is to integrate a set of specific models and perform multi-objective optimization of flight trajectories according to predetermined operational and environmental constraints. The models considered for this study include the Aircraft Performance Model, Engine Performance Simulation Model and the Gaseous Emissions Model. The paper, further discusses the results of a test case to demonstrate trade-offs between fuel consumption, flight time and NOx emissions that the trajectory optimization activity achieves at a primary level. It thereby forms the basis of a complete reference base-line trajectory which will be used to determine more accurate environmental gains that can be expected through optimization with the integration of more models within the framework in the future.
<Keywords: GATAC; Aircraft performance model; Engine Performance simulation Model; NOx emissions
The air transport industry today is paying a lot of attention to growing public concern about the environmental issues of air pollution, noise and climate change. The past decade has witnessed rapid changes both in the regulations for controlling emissions and in the technologies used to meet these regulations. Considering the critical nature of the problem regarding the environmental footprint of aviation several organizations worldwide have focused their efforts through large collaborative projects such as Clean Sky Joint Technical Initiative (JTI). Clean Sky is a European public private partnership between the aeronautical industry and the European Commission. It will advance the demonstration, integration and validation of different technologies making a major step towards the achievement of the environmental goals set by ACARE (Advisory Council for Aeronautics Research in Europe). The ACARE Vision 2020 and associated Strategic Research Agendas (SRAs) have successfully steered European aeronautics research in recent years by setting the objectives of reducing CO2 by 50%, NOx by 80% and Noise by 50% compared to year 2000 [1]. Ability to meet these challenges only is possible with a strong commitment to the vigorous evolution of technologies and achieving new breakthroughs. Over the last few years several alternatives have been proposed and most of them are long term solutions such as changing the aircraft and engine configurations and architectures. Hence all the manufacturers have started focusing and developing their strategies along the other possible options. The management of trajectory and mission is one of the key identified solutions found in achieving the above set goals and is a measure that can readily be implemented.
In order to truly understand the optimized environmental friendly trajectories it is necessary to simultaneously consider the combined effects of aircraft performance, propulsion system and engine performance, environmental emissions, noise and flying trajectories. GATAC (Green Aircraft Trajectories under ATM Constrains) is a multidisciplinary optimization frame work which is being collaboratively developed to achieve the above requirement by Cranfield University and other partners as part of the Systems for Green Operations - Integrated Technical Demonstrator (SGO-ITD) under the Clean Sky Joint Technical Initiative [1].
This section presents an overview of the main features and capabilities of the GATAC multi-disciplinary optimization framework. It can be considered as a state-of the-art optimization framework with optimizers and simulation models to perform multi-objective optimization of flight trajectories under Air Traffic Management (ATM) constraints. The top level structure of the GATAC framework is shown in Figure 1.
The framework consists of, the GATAC Core, Model Suite, Graphical User Interface (GUI) and Post-Processing Suite. It interacts with a suite of models as configured at set-up time. The GATAC core is the core engine of the interaction framework and provides the connectivity between the various models. It also provides for the organization of an evaluation process (within the Evaluation Handler) and includes functionalities such as parameter stores, data parsing, translation function and interfacing with models. It also supports the repeated calling of sets of models to enable trajectories to be evaluated step by step with number of steps being defined by the user at set-up time. The core, therefore, is programmable as the user sets-up the problem at hand within the Evaluation Handler by defining connectivity between models and any data translation and other similar functions. This can be done either directly using a purposely defined domain specific language or graphically via GUI. In this way, the user effectively defines (formulates) the optimization problem. The optimization process takes place in the GATAC Core, which accesses an optimization function chosen from a suite by the user [2,3].
A key feature of GATAC is that, he user can select any algorithm from the optimization suite without the need to modify the problem formulation because; the framework caters for normalization of data. Indeed, the algorithm in the optimization suite are designed to handle normalize variable parameters. The normalized parameters are then de-normalized by the integration framework as specified by the user before being input to the evaluation handler. Similarly the data that are output from the evaluation handler are again normalized before being input to the optimizer to close the optimization loop (Figure 1).
As the data exchanged between the optimization core and the models need to be defined according to the input and output data of each model and module. GATAC caters for the automatic definition of data structures by means of a dictionary. The automatic definition is carried out by GATAC at set-up time according to the output and input variables of the specific models and modules invoked in the problem definition. These data structures then enable the correct data transfer between the models and modules.
The GATAC can be run either on a single stand-alone machine or a distributed system with multiple computers (Figure 2). In the latter case the model suite is replicated on a number of different machines, on which a daemon will be running in the background. The daemon is even-triggered and instructed to run particular models by the Framework Manager, where the GATAC core resides. When its particular job is complete, the relevant daemon will return the results to the GATAC core. In this way, the core maintains full control of the optimization process. Data exchange between the GATAC core and the daemons is achieved through Ethernet LAN connectivity between the respective computers. The model suite is distributed on a single machine or different machines acting as hosts. The data exchange between components carried out through Ethernet LAN. The Figure 2 illustrates the architecture and operating network of the GATAC distributed system [2,3].
The NSGAMO (Non Dominated Sorting Genetic Algorithm Multi- Objective) is one of the genetic based optimizers incorporated in the GATAC framework. This optimizer is able to perform optimization of two objectives without or with constraints. Figure 3 shows the sequence of steps of the NSGAMO genetic algorithm.
According to the flowchart, at the first step an initial population of the test cases (candidate trajectories) is created randomly. The size of the initial population determined by the product of the prescribed population size with an initialization factor (>=1) A larger initial population size increases the probability of the optimizer converging to the global optimum point but slows down the optimization process. The optimizer then sends all the cases to the GATAC framework for the evaluation handler to evaluate and return the results (optimization objective) to the optimizer. On receipt of the results, the optimizer performs fitness evaluation on the data (i.e. qualifies the population). As optimum point is identified on the first generation, a second generation population is created and the process repeated. The process is repeated until convergence criteria are met (either a maximum number of generations will have been generated and evaluated or Pareto convergence will have been reached). In order to reduce the computational time of subsequent generation is reduced to prescribed population size. To achieve this only the best solution s of the previous population are selected to generate the next generation. New generations are created using different methods such as stochastic universal sampling, random selection and genetic operators (crossover and mutation). In the case of single objective optimization the result is the best-case while for a multi-objective optimization, the final result is a Pareto Front [3].
The implementation of the NSGAMO algorithm allows, for via a text file, the user definition of the various parameters associated with the optimization, which include population size, optimization method, mutation and crossover ratio, selection method and type of mutation and crossover and other parameters. A detailed description of the testing and benchmarking of the optimizer performance is presented in reference [4].
Engine model
The engine model developed for this study is based on Trent 895 which is a 3-spool high by-pass ratio turbofan engine with separate exhausts. The engine model is designated as CUHBR (Cranfield University High By-Pass Ratio) and was modeled using data available from public domain and making educated engineering assumptions where necessary. This engine has been selected to power the longrange aircraft which has been used to develop the aircraft performance model. The engine model has been developed and simulated using TURBOMATCH which is an in-house gas-turbine performance simulation and diagnostics software developed at Cranfield University [5]. The tool is used to model the design point of the engine and study its off-design performance. TURBOMATCH is a fully modular engine cycle simulator that can perform design point, off-design, steady state, and transient conditions as well as degraded performance analysis of gas turbines.
The TURBOMATCH engine model is assembled from a collection of existing interconnected elements called ‘Bricks’. Individual bricks are controlled by a numerical solver and represent the thermodynamic equivalent of gas turbine components including; intake, fan, compressor, combustion chamber, turbine, duct, and nozzle. Bricks are called up to model the architecture of the gas turbine and a numerical solver is used to solve the mass and energy balances between the interconnected bricks. TURBOMATCH also allows for the modeling of different fuels, extraction of bleed air and the shaft power off-takes, cooling air, component degradation, reheating, or sequential combustion etc. The outputs from the tool include the calculation of the overall performance of the engine in terms of gross and net thrust, fuel flow, Specific Fuel Consumption (SFC) as well as the thermodynamic parameters and gas properties at the inlet and outlet of each component. Detailed operational parameters such as efficiency, rotational speed, power required/power delivered, surge margin in case of the fan and compressor or thrust coefficients in the case of nozzles, are also provided. For the purpose of this study, the engine is modeled by developing a representative input file that represents the configuration of the CUHBR engine. Figure 4 is a schematic of the CUHBR TURBOMATCH model.
As shown in the figure, the LP turbine drives the fan. Similarly, IP turbine and HP turbine drive the IP compressor and HP compressor respectively. It has been assumed that part of the air is bleed from the HP compressor to cool the HP turbine and no cooling air bleeds for the IP turbine and LP turbines. The secondary air system has been largely simplified and handling bleed has not been considered.
The engine design point has been selected at maximum rated thrust during take-off under ambient International Standard Atmospheric (ISA) conditions at sea level, and the engine mass flow, bypass ratio and overall pressure ratio have been obtained from the public domain. An iterative trial and error process has been required in order to match the performance of the engine model with the reference engine performance data at DP as well as cruise phase. At the design point assumptions are made with regards to the pressure ratio split between the compressors, component efficiencies, surge margin, cooling mass flows, duct/intake and burner pressure losses, burner efficiency, as well as bleed and power off-takes. The fan pressure ratio is iterated and optimized for the maximum thrust and minimum SFC. The Turbine Entry Temperature (TET) of the cycle is iterated until the calculated thrust and the fuel consumption match the values found in the public domain with marginal difference. Being the differences in percentage about 2% the engine model can be considered verified for the scope of this project. The performance comparison of the CUHPR engine and summary of component specifications are shown in the Table 1 and 2 respectively.
| Parameter | Value | Unit |
|---|---|---|
| Engine Mass Flow | 1,208 | Kg/S |
| Overall Pressure Ratio | 41.7 | |
| Bypass Ratio | 5.8 | |
| Fan Pressure Ratio | 1.81 | |
| Ipc Pressure Ratio | 4.79 | |
| Hpc Pressure Ratio | 4.79 | |
| Fan Efficiency | 89.5 | % |
| Ipc Efficiency | 88 | % |
| Hpc Efficiency | 88 | % |
| Combustor Efficiency | 99.9 | % |
| Combustional Fractional Pressure Loss | 5 | % |
| Turbine Inlet Temperature | 1,771 | K |
| Hpt Cooling Flow | 13 | % |
| Hpt Efficiency | 89 | % |
| Ipt Efficiency | 90 | % |
| Lpt Efficiency | 91 | % |
Table 1: Cuhbr Engine Performance At Design Point [Take-Off Is A Sls Condition].
| TAKE-OFF | CRUISE | |||||
|---|---|---|---|---|---|---|
| T895 | CUHBR | % | T895 | CUHBR | % | |
| W (Kg/S) | 1,208 | 1,208 | 0.00 | - | 441.0 | - |
| FPR | 1.81 | 1.81 | 0.00 | - | 1.66 | - |
| BPR | 5.8 | 5.8 | 0.04 | - | 6.551 | - |
| PR | 41.6 | 41.6 | 0.00 | - | 32.66 | - |
| TET[K] | - | 1771 | - | - | 1383 | - |
| Wf [Kg/S] | - | 4.19 | - | - | 0.972 | - |
| SFC [Mg/Ns] | - | 9.90 | - | - | 16.20 | 2.14 |
| Fn [Kn] | 422.6 | 422.8 | 0.04 | - | 60.01 | -0.06 |
| Wc [Kg/S] | 178.2 | 177.6 | -0.35 | - | 4.00 | - |
Table 2: Real Engine Vs Engine Model Performance.
With the fixed design point, a series of Off-Design (OD) performance simulations have been performed in order to simulate the effects of ambient temperature, altitude, flight Mach number and TET on net thrust and SFC as a further model verification process. The Figure 5 and 6 shows the variation of net thrust and specific fuel consumption for different flight Mach numbers at different altitudes under OD performance.
As the flight velocity increases the performance of the engine is influenced by three main factors: momentum drag, ram compression and ram temperature rise. The momentum drag rises with the flight speed with a consequence reduction of the momentum imparted to the air by the engine. Therefore, the net thrust, which is defined as the difference between gross thrust and intake momentum drag, drops with the rising of flight Mach number. The second effect is the ram compression and it has a double effect. Firstly, it increases the nozzle pressure ratio and therefore the net thrust. Secondly, it raises the inlet pressure and thus air density along with mass flow. The last effect is the ram temperature rise, which produces an increment of air temperature at fan inlet. This leads, at constant shaft speed, to a decrement of non-dimensional power setting and hence thermal efficiency. The momentum drag and the ram compression are generally the main effects. At low speed, momentum drag is the main effect and the net thrust drops quickly with the rising of flight speed. Since Mach number is less than 0.3 the effects of temperature rise and am compression are small. At higher Mach number the effect of compressor rise starts to be important and, as it is possible to observe, the gradual decrease in net thrust.
As shown in Figure 5 the net thrust decreases when the altitude increases with a constant Mach number. When the altitude increases the air density drops, leading to a reduction of mass flow and hence net thrust. The reduction of air density does not alter the non-dimensional power setting of the engine. Moreover, in the troposphere the reduction of net thrust due to the drop of the air density is in partly offset by the positive effect of the decrement in ambient temperature. Indeed, the ambient temperature falls linearly in the troposphere, from 15°C at sea level to -56°C at the top of the Troposphere at 11 km. At constant shaft speed, when the temperature drops the non-dimensional power setting raises leading to an increment in pressure ratio therefore in net-thrust. Figure 6 shows how the increases with flight Mach number. In order to fly at faster speed more fuel is required. The increment of the fuel flow overcomes the decreasing on net thrust and rises with Mach number.
In Figure 7 and 8 are the effects of ambient temperature and on net thrust and are shown. At low TET give rise to low thermal efficiency and jet velocity which create a high propulsive efficiency which resulted in high SFC. Similarly at high TET leads to give high thermal efficiency and high jet velocity which result in low propulsive efficiency. The figure 7 shows the best compromise between thermal efficiency and propulsive efficiency for several ISA deviations.
With the variation of ambient temperature there are two main effects that have to be considered [6]. The first effect is well described in Figure 9 whereas considering an ideal cycle between fixed values of overall pressure ratio is shown.
Figure 9 shows that on a ‘hot day’ the compressor work will be greater than in a ‘normal day’. This is due to the fact that compressing hot air requires more work. However, the turbine’s work is not affected by ambient temperature because in this case the overall pressure ratio does not change. Consequently on a hot day, the difference between turbine work and compressor work will be less than the normal day therefore the net thrusts will decrease. Also this effect is reflected with a shift in compressor operating point with a variation in ambient temperature. This is due to the fact that, the non-dimensional rotational speed 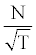 depends on shaft speed and temperature. Assuming constant the rotational speed of the shaft, in a hot day the ambient temperature increases and hence the non-dimensional rotational speed decreases. Therefore, the operating point will move to the left and downwards so the pressure ratio and the non-dimensional mass flow will decrease. The opposite will occur in a cold day. For constant ambient temperature, with the increment of the pressure ratio and net thrust increase. For constant with the rising of ambient temperature the net thrust drops. Vice versa, with the decrement of ambient temperature the net thrust rises.
depends on shaft speed and temperature. Assuming constant the rotational speed of the shaft, in a hot day the ambient temperature increases and hence the non-dimensional rotational speed decreases. Therefore, the operating point will move to the left and downwards so the pressure ratio and the non-dimensional mass flow will decrease. The opposite will occur in a cold day. For constant ambient temperature, with the increment of the pressure ratio and net thrust increase. For constant with the rising of ambient temperature the net thrust drops. Vice versa, with the decrement of ambient temperature the net thrust rises.
The software that has been used to simulate the integrated aircraftengine performance is called HERMES. It has been developed at Cranfield University in order to assess the potential benefit of adopting new aircrafts, engine concepts and technologies [7]. The aircraft model is capable to simulate the performance of different types of aircrafts, from a baseline aircraft to an advanced one for a given civil mission. The software consists of six different modules;
a. Input data
b. Mission profile module
c. Atmospheric module
d. Engine module
e. Aerodynamic module
f. Aircraft performance module
The aircraft model computation starts reading the required input data from an input file. As described below, these data regard the general arrangement of the aircraft and mission profile. Some of these data are usually available from the public domain or defined by the user. The user has to specify as an input the MTOW and the weight of the payload. Moreover, the user has to set either the fuel load or the mission range. In the first case HERMES will compute the mission range whilst in the second case HERMES will assess the required amount of fuel to complete the mission. In the case that the user has set the initial amount of fuel, the value of the range will be considered as an initial guess and will not influence the resulting values.
The range is calculated iteratively. In each iteration process the fuel required for a trial distance is computed. As soon as the total fuel is consumed the convergence is achieved. This is obtained calculating the trial OEW by subtracting the assessed total fuel, which is given by the sum of mission fuel plus reserve, and the payload from the MTOW. The trial OEW is then compared with the OEW set up in the input file and the difference is used to redefine the distance and the time spent at the cruise. The convergence is achieved when the difference of OEW is within 0.1 %.
Input data module
The input data required for the aircraft model are information regarding the geometry, configuration and the required performance of the aircraft. These input data are used by the aircraft performance and aerodynamic modules to calculate the performance and aerodynamics characteristics of the aircraft.
Mission profile module
The mission profile is subdivided into different phases. The overall mission profile is defined by the user and is used by the aircraft performance module to compute the distance, fuel and time for each the each segment in which the mission is subdivide. In addition, TURBOMATCH refers to the mission profile in order to calculate the engine performance.
Atmospheric module
The atmospheric conditions for a given Mach number and altitude have a great influence on the aircraft and engine performance. Therefore, the atmospheric module calculates the ISA conditions both in the lower atmosphere and stratosphere. Moreover, the user has the possibility to alter the temperature from ISA standard values to simulate non-standard conditions.
Engine data module
The performance of the engine greatly influences the aircraft performance. The engine data usually includes, maximum take-off thrust: required to assess the length, fuel and time required for the take-off; maximum climb thrust and SFC: required to compute fuel consumed, horizontal distance covered, rate of climb and time to climb; cruise and descent performance.
Aerodynamic module
Calculates the aerodynamic performance of the aircraft for the given flight conditions. The module elaborates the information regarding the mission profile, the aircraft and aerodynamics properties in order to compute the drag characteristics in form of drag polar profile and drag coefficients.
The drag polar can be always expressed using two main components of drag; one is dependent on lift and the other independent on lift. Therefore, the total drag coefficient can be expressed using the following equation:
CD = CD0 + CD1
The term CDO is the zero lift drag coefficient and is a constant while CD1 is the lift dependent drag or induced drag coefficient and it can be expressed as follows:
CDI = K . CL2
Where K is called lift dependent factor. Combining the previous two expressions it is possible to write the well-known drag coefficient expression:
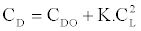
The calculation of the zero lift drag coefficient is performed using the component build-up method, which has the following general expression [5]:
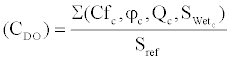
The flat-plate skin friction coefficient Cf and the form factor φ, which estimates the pressure drag due to viscous effects, are used to assess the subsonic profile drag of a particular component. The factor is Q used in order to take into account the effects of the interference drag on the component. As highlight in the previous equation, the product of the wetted surface of the component, SWet and Cf, φ and Q allows to calculate the total drag on the component, c. Using this method it is possible to calculate the drag arising from several components such as fuselage, tail plane, fins, nacelle, outer wings and engine pylons. It also allows the estimation of miscellaneous drag arising from deployed flaps, landing gear and trim conditions. The coefficient CDO is then calculated dividing the total drag by the reference area Sref, which is the plan wing area.
The lift induced drag is estimated using the following equation [8]:
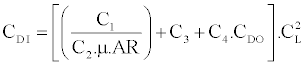
Where the coefficients C1 and C2 are a function of the wing aspect ratio and taper ratio and are used to take into account the wing plan form geometry. The coefficient C3 and C4 are used to account the non-optimum wing twist and viscous effect respectively.
Aircraft performance module
Information from the other modules is passed to the aircraft performance module. In turn, the aircraft performance module computes the overall performance of the aircraft for each segment in which the entire mission is divided.
Typical outputs include: fuel consumption, distance covered, mission duration, engine thrust and SFC for the whole, mission and for each flight segment.
The calculations of the climb rely on the rate of climb, which is defined as the ratio between the change in height and the time assuming zero wind velocity:
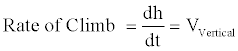
During the calculation of the rate of climb appropriate acceleration factors are included in order to take into account the following cases:
• When the aircraft is climbing in the stratosphere, the ambient temperature reduces, thus at constant Mach number the airspeed decreases because the speed of sound drops.
• During a climb at constant equivalent air speed the true air speed is increasing because the air density drops with altitude.
Therefore, the time required to flight from an altitude h1 to an altitude h2 is given by the following expression:
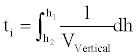
The flight distance, the time and the fuel consumed (thus aircraft weight) at the end of each segment are a function of the rate of limb. In turn the rate of climb relies on thrust, drag and mass of the aircraft. The integration of the previous equation is therefore complicated to compute because of numerous interrelationships regarding the variables involved. For this reason the model used an iterative procedure with the estimation of the weight and the time at the end of each segment, which are then used to compute the correct values.
The total time of the climb phase is given by the sum of the time of each segment:
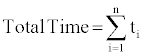
Using the climb speed and gradient it is possible to work out the horizontal distance covered by the aircraft:
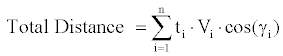
Similarly, the total fuel is computed by summing the fuel burnt in each interval.
The calculation of the flight range is a function of the engine and aircraft parameters and the available quantity of fuel. In order to derive the equations implemented in the aircraft performance module it is necessary to define some fundamental variables that are involved.
Firstly, for an aircraft in horizontal, steady state flight at constant true airspeed V, the engine thrust has to be equal so the aerodynamic drag. Therefore it is possible to write:
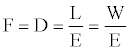
Where F is the engines thrust, D and L are the drag and lift of the aircraft respectively W is the aircraft weight and E is the aerodynamic efficiency, which is defined as the ratio between the lift and the drag. Considering the definition of lift and the drag forces, the aerodynamic efficiency can be expressed as follows:
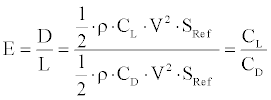
Where ρ is the density of the air and SRef is the wing plan area. The specific fuel consumption, SFC, of an aircraft powered by a turbojet or turbofan engine is defined as the ratio of fuel flow (Q) per specific thrust (FS):
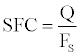
The specific range ra is defined as the flight distance dR per unit of fuel consumed so:
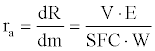
The integration of the above equation leads to compute the total cruise range:
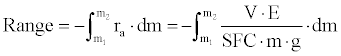
Where m1 and m2 are the initial and final mass of the aircraft during the cruise. In order to be able to integrate the range equation it is necessary to express the variables V, E and SFC as a function of the aircraft mass (m).
Three different flight schedules can be chosen which lead to three different sets of assumptions for the variables:
• Cruise at constant altitude, SFC and lift coefficient;
• Cruise at constant airspeed, SFC and lift coefficient;
• Cruise at constant altitude, airspeed and SFC
Usually the second option is used. Therefore the lift coefficient, expressed as following:
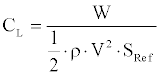
Has to remain constant. This allows concluding that the ratio of the aircraft weight to the air density has to remain constant. During the cruise the fuel is consumed thus the weight of the aircraft decreases and the density has to decrease accordingly. This can be achieved allowing the aircraft to climb. At the same time, with the decrement in air density the thrust will decrease and it can be assumed that the true air speed is constant.
In practice the aircraft are not allowed to climb during cruise by the air traffic control so airlines adopt a stepped climb procedure. For each segment at constant altitude, it is possible rewrite the range equation considering constant SFC airspeed and lift coefficient:
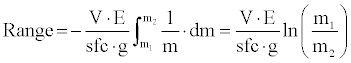
This equation of range is known as Brequet equation. A variant to solve the basic range equation is using a numerical integration dividing the mass variation in intervals:
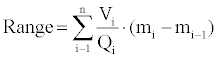
In HERMES a similar approach of the integrated range method has been implemented. However, instead of dividing the mass into intervals and then calculating fuel consumed and range, the cruise is split into intervals of time.
Weight variation during the time for an aircraft flying horizontally is given by the following equation:
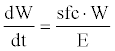
and integrating the previous equation respect to the time:
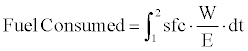
onsidering n intervals the total fuel consumed can be worked out as follows:
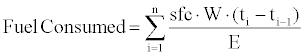
At each interval the range is equal to:
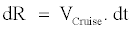
The total range is the sum of the flight range for each interval. As pointed out above, in order to improve the overall efficiency of the aircraft the airliners allow performing what it is known as step climb cruise. Similarly, the user can subdivide the cruise into intervals and specify for each interval different flight Mach numbers and altitudes.
During the descent phase the drag of the aircraft is greater than the thrust produced by the engine leading the aircraft to glide. The descent starts at cruise Mach number and it reduced till the 250 knots at sea level. The calculation of the descent phase is similar to the climb calculation presented above (Figure 10). The user has to set up in the mission profile input file the different intervals of the descent phase. Using an iterative method the flight time, rate of descent and horizontal distance covered are assessed.
The aircraft model developed in this project is designated as LRACM (Long Range Aircraft Model). The LRACM model is based on the performance data of a typical twin-engined turbofan long range civil aircraft LRACPD (Long Range Aircraft Public Domain) available in public domain. As mentioned before, in order to configure the aircraft model it is required to setup an input file with several parameters, including, aircraft geometry, configuration, mission profile and weight breakdown.
Table 3 reports the main performance parameters regarding the LRACPD available from the public domain.
| PARAMETER | VALUE | UNIT |
|---|---|---|
| PAASENGERS | 301 | |
| ENGINES | Trent 895 | |
| MAXIMUM TAXI WEIGHT | 298,460 | Kg |
| MAXIMUM TAKE-OFF WEIGHT | 297,550 | Kg |
| MAXIMUM PAYLOAD WEIGHT | 59,430 | Kg |
| MAXIMUM LANDING WEIGHT | 213,180 | Kg |
| MAXIMUM ZERO FUEL WEIGHT | 199,580 | Kg |
| OPERATING EMPTY WEIGHT | 141,880 | Kg |
| FUEL CAPACITY | 171,170 | Kg |
| Cruise Mach Number | 0.84 |
Table 3: Performance Summary of Lracpd.
Regarding the geometry of the aircraft and the engine in some of the required information is listed. Some of the parameters are not available in the literature therefore they have been assumed.
The accuracy of the aircraft model has been verified against published data using the payload-range diagram. In this diagram the aircraft range is plotted against the payload (Table 4). There are usually three-baseline aircraft configurations, including:
| PARAMETERS | VALUE | UNIT | |
|---|---|---|---|
| FUELSAGE | LENGTH | 63 | M |
| DIAMETER | 6 | M | |
| WING | AREA | 428 | M2 |
| ASPECT RATIO | 9 | ||
| TAIL PLANE | AREA | 101 | M2 |
| ASPECT RATIO | 5 | ||
| TAPER RATIO | 0.3 | ||
| FIN | AREA | 53 | M2 |
| ASPECT RATIO | 5 | ||
| TAPER RATIO | 46 | ||
| ENGINE | DIAMETER | 3 | M |
| LENGTH | 7 | M |
Table 4: Aircraft and Engine Model Geometry.
• Maximum Payload range;
• Maximum economic range;
• Ferry range.
In the maximum payload range the aircraft take-off with both maximum take-off weight and maximum payload weight. Therefore, the amount of fuel is given by the following equation:
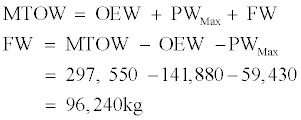
In the maximum economic range, similarly to the previous case aircraft take-off with its maximum take-off weight, but this time with the maximum amount of fuel. Therefore the range will increase. The amount of carried payload is given by:
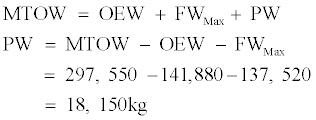
Regarding the ferry range, the aircraft take-off with no payload and with the maximum amount of fuel. The ferry range is the maximum range of the aircraft. The take-off weight is given by the following equation:
TOW=OEW+PWMax=297,550+141,880=493,350 kg
Considering that the initial amount of fuel was known for each mission using HERMES the flight range has been calculated and compared with published data.
Figure 11 shows the comparison between the payload range diagram of LRACPD and the aircraft model. Due to the lack of more information a step cruise from 10,000 to 11,000 meters was assumed.
In Table 5 shows the values of the payload and fuel weight are reported for each mission along with the difference between the range of the real aircraft and the model.
| Maxim Payload | Economy | Ferry | Unit | |
|---|---|---|---|---|
| Payload Weight | 59,430 | 18,150 | 0 | Kg |
| Fuel Weight | 96,240 | 137,520 | 137,520 | Kg |
| LRACM | 10,200 | 15,890 | 17,060 | Km |
| LRACPD | 10,010 | 15,870 | 17,190 | Km |
| Difference | 1.82 | 0.15 | -0.74 | % |
Table 5: Aircraft Model Validation.
The emission prediction model used in this work is the P3T3 empirical correlation model which has been integrated as part of Cranfield University HEPHASTUS emission prediction tool. This model estimates the level of emissions at altitude using a correlation with the emissions measured at ground level. This methodology is straightforward. Firstly, during the certification test of the engine the emission indices are measured. These indices are subsequently corrected to take into account the variation of altitude and flight speed. In order to do that, it is necessary to know the combustion parameters for the operating conditions at both ground level and altitude. These parameters are: burner inlet pressure and temperature, fuel and air ratio and fuel flow. In addition the model takes into account the variation of humidity from the sea level to altitude. The model is capable of predicting all the emissions and in this paper main focus given to the NOx emissions only. Detailed model layout shown is shown in Figure 12.
The engine tests results published by ICAO the level of emissions and other main parameters are measured for different engine operating conditions. These conditions are:
1. Take-off: full power (maximum level of thrust);
2. Climb out: 85% of take-off thrust;
3. Approach: 30% of Take-off thrust;
4. Idle: 7% of Take-off thrust.
EINOX measurements at ground level are plotted for different combustor inlet temperatures. Moreover, as explained above, in order to calculate the emissions at certain flight altitude and speed, the combustor inlet temperature, inlet pressure and air mass flow have to be known. Even if these values are not measured during the ICAO tests they can be assessed using gas turbine performance simulation software. At this point, similarly to EINOX, burner inlet pressure and FAR are plotted for different burner inlet temperatures. Then, using the combustor inlet temperature at altitude it is possible to obtain the respective value of EINOX at ground level from the specific plot. This value of EINOX is then corrected for taking into account the differences in FAR and inlet combustor pressure between ground level and altitude. The values of exponent and establish the severity of EINOX correction. Finally, a correction for the humidity influence is also taken into account. Having calculated the value of EINOX, the emitted NOX in kilograms is given by:
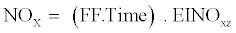
Where FF, is the fuel flow in [kg/s], and the time in seconds.
The variation of humidity change with the altitude relative to ISA sea level is taken into consideration. The correction increases with increasing altitude. If the measurement of EINOX at sea level has been done in a day with a high level of relative humidity, say 60%, the correction with the altitude will increase EINOX by around 12.5%. At typical cruise altitude the error by choosing different curves of relative humidity is small because the air is dry. ICAO suggests using 60% of relative humidity for calculations [9]. Engine manufactures during the years have gathered a large amount of data from engine testing, which have facilitated in defining the pressure coefficient to be set in the model. In the rig tests the combustor inlet conditions are varied independently in order to establish their relative effect on NOX formation. The value of pressure exponent is commonly in the range between 0.3 and 0.5 in typical cruise condition [10]. This value varies as a function of the combustor type, operating conditions and measurement variability. An average value of 0.4 is normally used for all civil aircraft engines. Regarding the FAR, the data from the engine manufacturers shows that during the cruise the FAR is 10% richer than at ground level with constant combustor inlet temperature.
The main advantage of using the P3T3 model relative to other emissions models such as the physics based stirred reactor model is the low computational time required because it is based on empirical correlations. The required computational time is a key feature for a model that has to be used in aircraft multi-objectives trajectory optimization study considering the large amount of calculations involved.
The file used to setup the engine emission model requires information about engine emissions, the combustor inlet pressure and temperature, the fuel flow and the fuel/air ratio for the four operating conditions at ground level.
In the ICAO database it is possible to find only data regarding the emissions indices. Therefore, the values of combustor inlet temperature and pressure, fuel flow and fuel/air ratio have to be assessed using an engine simulation tool. TURBOMATCH has been used for this work. Table 6 indicates the relevant data available from the ICAO engine database:
| Mode | Power Setting [% TOT] | Fuel Flow [Kg/S] | EIHC [G/Kg] | CO [G/Kg] | Nox [G/Kg] |
|---|---|---|---|---|---|
| Take-Off | 100 | 4.03 | 0.02 | 0.27 | 47.79 |
| Climb Out | 75 | 3.19 | 0 | 0.19 | 34.29 |
| Approach | 30 | 1.05 | 0 | 0.54 | 11.39 |
| Idle | 7 | 0.33 | 0.89 | 14.71 | 5.11 |
Table 6: Icao Engine Emmisions Data Bank.
As it is possible to notice from the Table 5 only the fuel flow and the emissions indices are available along with the power setting of each mission phase, a series of off-design simulations has been carried out using TURBOMATCH in order to find the other necessary performance data of the engine. In the OD section of the engine model input file the value TET for each phase of the mission will be taken to match the values of the fuel flow with ICAO database. In Table 7 compare the fuel flows of the engine model under different flight phases with the public domain data available in ICAO. Then, the values of pressure and temperature at the burner inlet and the fuel/air ratio have been set in the emission model input file.
| Mode | ICAO Fuel Flow [Kg/S] | CUHBR Fuel Flow [Kg/S] | Difference [%] |
|---|---|---|---|
| Idle | 0.33 | 0.33 | 0.27 |
| Approach | 1.05 | 1.03 | -1.63 |
| Climb Out | 3.19 | 3.10 | -2.84 |
| Take-Off | 4.03 | 3.86 | -4.17 |
Table 7: Emmision Model Setup–Sea Level Isa Condition.
In this study the entire flight profile has been divided in to three main phases: climb, cruise and descent. Three parameters have been used to define the flight trajectory: aircraft speed (M, TAS and EAS), flight altitude and mission range. The mission range has been kept constant for the all optimization studies. Therefore the study has been mainly focused on the trajectory optimization between two-fixed destinations. The climb and cruise phases are simply defined using 18 points and the cruise Mach number.
However, in the optimization process only six design variables have been considered in order to reduce the required computational time. These design variables are: five values of altitude and the cruise Mach number. The first four values of altitude are used to define the climb trajectory whilst the last altitude point defines the cruise altitude, which is constant for the entire cruise. The other points are computed by interpolation between two consecutive design variables maintaining constant increment in altitude.
For each design variable a boundary has been set to ensure that the resulting optimized trajectories were both feasible and with constant rising climb altitude. These boundaries can be considered as explicit constraints since they are directly applied to the design variables. Table 8 shows the limitation values for each design variable. A gap in altitude between two consecutive variables has been considered in order to guarantee a constant increment in altitude.
| Design Variable | Min Value | Max Value | Unit |
| Climb Altitude 1 | 1,000 | 2,400 | M |
| Climb Altitude 2 | 2,700 | 4,400 | M |
| Climb Altitude 3 | 4,800 | 6,400 | M |
| Climb Altitude 4 | 7,000 | 8,400 | M |
| Climb Altitude 5 | 9,000 | 11,000 | M |
| Cruise Mach Number | 0.75 | 0.85 |
Table 8: Trajectory Designs Variables and Their Boundaries.
Speed (EAS) during climb was fixed with the aircraft performance input file to 250 knots for the first two climb segment and 320 knots for the three subsequent climb segments. Moreover, climb and descent phases are flown at fixed power setting. For both phases maximum power setting is selected, i.e. maximum thrust at maximum TET permitted in the given flight phase. According to Laskaridis et al. [8] a common method to climb is at constant EAS.
As it is shown in Table 8 the maximum allowable altitude has been limited to 11,000 meters. This limitation is related to the fact that, as altitude increases, the Reynolds number falls because the ratio density to absolute viscosity drops. At certain altitude, the Reynolds number will fall below a critical value of 105 and the flows about the blades of compressors and turbines will start to separate. This situation leads to two main consequences: (a) The flow is not deflected as much as before thus the compressors and turbines power drops leading a reduction of thrust; (b) SFC increases because of the increment in losses associated with the turbulent wakes that, in turn, cause a reduction of compressors and turbines efficiencies.
According to Pilidis [6] at an altitude of 11,000 meters, for a large turbofan, the effect due to the drop of Reynolds number lead a reduction about 2 % of thrust. In the engine performance model adopted in this work the effect of Reynolds number is not taken into account. Therefore a limitation of 11,000 meters has been considered in order to obtain more realistic results.
The descent trajectory starts at cruise altitude and speed and it has been divided into 10 segments. For each segment the flight speed has been chosen as it is stated in Table 9.
| Power Setting During Descent | TAS | Unit |
|---|---|---|
| Idle | 223 | Knots |
| Idle | 221 | Knots |
| Idle | 202 | Knots |
| Idle | 195 | Knots |
| Idle | 183 | Knots |
| Idle | 164 | Knots |
| Idle | 150 | Knots |
| Approach | 140 | Knots |
| Approach | 135 | Knots |
| Approach | 135 | Knots |
Table 9: Descent Phase Power Setting and Tas.
The overall optimization running sequence is shown in Figure 13. At the start of the optimization process the optimizer (GATAC) generates the first set of design variables. In this work the design variables are five altitude points and the cruise Mach number. The first four altitude points describe the climb trajectory whilst the last point corresponds to the altitude of the cruise.
The design variables are written in the input file of the aircraft model along with all the other required parameters. The following step consists in the execution of the aircraft model. As already explained, the aircraft model also requires the specifications about the aircraft and engine performance data.
The execution of the aircraft model generates two output files. The first file regards the aircraft performance. The results include mission duration, fuel consumption and distance covered for the whole mission and for each flight segment. The second file contains the performance of the engine for each phase of the mission. SFC, thrust, shaft speed as well as engine temperatures and pressures can be found in this file.
Information regarding the mission profile, fuel consumed and engine performances during the mission are used to generate the input file for the emission model. In addition, the emission model required other data regarding combustion specification and engine emission. These data are read from a specific input file. The emission prediction model computes the values of NOX, CO, UHC emitted during the mission in kilograms. Then, the output data are read by GATAC and, based on these values; a new generation of design variables are created. This process is repeated till the integrated optimisation criteria are satisfied.
A number of assumptions have been required in the present study, including:
1. A procedure is implemented in the aircraft model to ensure that each point, which defines the climb trajectory, has a higher altitude of the previous one.
2. The cruise phase is flown at constant altitude and constant flight Mach number;
3. The climb phase is flown at constant power setting. This means that the profile generated for every range and altitude selected is nearly the same;
4. The descent phase not taken for the optimization process.
5. The user cannot choose arbitrary descent profile and it is automatically calculated by the HERMES code by interpolation between the cruise altitude and the landing altitude. Therefore, the descent profile is a function of the cruise altitude only;
6. The continuity of the flight speed has not been guaranteed between the cruise and the descent phase. This could be cause variation of flight speed between cruise and descent phase;
7. For simplicity, taxi phases, take-off and landing have not been included in the mission profile and hence in the overall calculation and optimization. The consequence is that the total flight range considered by the optimizer comprises only climb, cruise and descent. The climb phase starts at 475 meters of altitude whilst the descent phase terminates at sea level altitude;
8. Although in HERMES it is possible to take into account the flight diversion mission, it has not been considered in this work;
9. A deviation of +3 degrees has been assumed respect ISA conditions for the entire mission.
Following section presents the different optimization studies carried out in the GATAC framework. In each the aircraft flight trajectory which has been optimized keeping the aircraft and engine configurations unchanged including the payload equivalent to 301 passengers. As stated in the above section the design variables utilized are associated with flight altitude during the climb and cruise phases and aircraft flight Mach number during cruise. The trade-offs of conflicting objectives such as flight time, fuel burnt and NOX emitted have been considered under each case study (Table 10).
| Parameter | Minimum Fuel | Minimum Time | Unit |
|---|---|---|---|
| Altitude 1 | 2,200 | 2,200 | M |
| Altitude 2 | 2,700 | 2,700 | M |
| Altitude 3 | 4,802 | 4,800 | M |
| Altitude 4 | 7,000 | 8,220 | M |
| Altitude 5 | 11,000 | 9,000 | M |
| Mach Number | 0.804 | 0.85 |
Table 10: Variables Corresponding To Optimum Fuel and Time Trajectories.
Case 1: fuel burnt vs flight time
This optimization study has been carried out for two conflicting objectives: minimum fuel burnt and minimum flight time. No other constrains were applied. Figure 14 illustrates the Pareto front obtained with the GATAC NSGAMO optimizer [11]. The mission range was set equal to 14,195 kilometers.
The Pareto curves were generated from 100 and 300 generations with series of points, where each point represents a trajectory, with its combination of design variables (altitudes and Mach number). For each point of the Pareto curve it is impossible to minimize further any objective from points given in the Pareto front. In Figure 14 the point A corresponds to the trajectory of minimum fuel consumed and the point B refers to the minimum flight time trajectories. The remaining points are other intermediate solutions. In the case of a trade-off between two conflicting objectives there is no a unique optimum solution or trajectory but the solution consists of a series of optimum trajectories with their unique combinations of time and fuel.
The two trajectories lead to important differences in terms of flight time, fuel burnt and emissions. This was expected considering the trade-off between minimum fuel and minimum flight time. The two trajectories differ of 8.63% (79 min) in flight time and about 12.27% (14,790 kg) in fuel burnt. Less fuel burnt means less emission of NOX and CO2. While the emission of CO2 is directly related with fuel burnt, the relation between NOX and fuel is different, as it will be described in the following sections. However, the fuel-optimized trajectory leads to higher emissions during the descent phase than the time-optimized trajectory. Considering that the aircraft is flying at higher altitude in the fuel-optimized trajectory the descent phase will be longer. Moreover, differently from the climb phase, the descent phase is fixed and it is not part of the optimization process. The two trajectories are shown in Figure 15 based on the selected design variables in Table 11.
| Parameter | Unit | Min Nox | Min Time | Diff [%] |
|---|---|---|---|---|
| Flight Time | Min | 1,065 | 916 | 13.96 |
| Fuel Burnt | Tons | 106.74 | 120.53 | -12.91 |
| Total Nox | Tons | 1.46 | 1.97 | -35.07 |
| Nox Climb | Tons | 0.14 | 0.16 | -9.50 |
| Nox Cruise | Tons | 1.31 | 1.81 | -38.11 |
| Nox Descent | Tons | 6.6 | 5.7 | 13.89 |
| Total CO2 | Tons | 337.44 | 380.69 | -12.82 |
| CO2 Climb | Tons | 16.94 | 18.33 | -8.16 |
| CO2 Cruise | Tons | 318.46 | 360.68 | -13.26 |
| CO2 Descent | Tons | 2.03 | 1.69 | 17.15 |
Table 11: Results Comparison-Time Vs Nox.
| Parameter | Minimum Nox | Minimum Time | Unit |
|---|---|---|---|
| Altitude 1 | 2,200 | 2,200 | M |
| Altitude 2 | 2,700 | 2,700 | M |
| Altitude 3 | 5,105 | 5,167 | M |
| Altitude 4 | 7,000 | 8,400 | M |
| Altitude 5 | 11,000 | 9,000 | M |
| Mach Number | 0.75 | 0.85 |
Table 12: Variables Corresponding To Optimum Nox and Time Trajectories.
In order to minimize the fuel burnt the optimizer suggests a solution where the aircraft flies the cruise phase at highest possible altitude 11,000 meters and Mach number equal to 0.804.
Generally, decreasing the speed and increasing the altitude lead to a decrement in drag and therefore in required thrust. This lower thrust requirement, in turn, means lower engine power setting along with lower fuel burnt. However, other important aspects have to be considered. A reduction in flight speed means more flight time with a negative effect on the fuel burnt. Therefore the optimizer has to assess the best compromise. In this case the resulting cruise Mach number for minimum fuel burnt trajectory is 0.804, which is higher than the minimum allowed value that was set to 0.75.
Moreover, in order to reach as quickly as possible the highest allowable altitude an increment of engine thrust and power setting is also required. It is interesting to notice in Figure 16 how the optimizer for the fuel-optimized trajectory proposes segment 17 affording a much greater fuel consumption respect to the time-optimized trajectory. This is done in order to gain height as quickly as possible, which leads to lower fuel consumption for the following segments. In Figure 16 it is worth noting that the climb phase comprises the first 18 segments and the following segments represent the cruise phase.
The minimum flight time means maximum TAS. Therefore in order to minimize the time during the cruise the aircraft flies at the highest Mach number permitted, which is 0.85. The optimizer suggests also flying at lowest altitude. This is correct since the speed of sound is highest at sea level along with TAS. Moreover, as already explained, the thrust increases with the decreasing in altitude because of the air density. The altitude profile of the two climb trajectories is shown in Figure 17
Again, it is possible to notice that the climb gradient of the fuel-optimized trajectory is greater than the time-optimized one. The aircraft has to accelerate as faster as possible in order to gain height. The acceleration to gain height for the fuel-optimized trajectory is well shown in Figure 18. The step in the flight Mach number is due to the passage from 250 knots to 320 knots of EAS during the climb phase as described above.
Case 2: minimum flight time vs minimum nox emitted
The next study that has been carried out regards the optimization of two conflicting objectives: minimum flight time and minimum NOX emitted. It is important bearing in mind that optimizing for fuel consumption is different from optimizing for NOX emissions. Similarly to the previous case, the trade-off of the two objectives leads to the characteristic of the Pareto curve shown in Figure 19.
The point C and D represent the minimum flight time and minimum NOx trajectories respectively. A comparison of the results considering Time and NOX optimized trajectories is shown in Table 11.
The minimum flight time trajectory has exactly the same values of flight time, fuel burnt and emissions already calculated in Case1. Regarding the NOX-optimized trajectory, the total NOX emitted is about 1,457 kilograms and the reduction is up to 35.07% compared with the time-optimized trajectory. In the fuel optimized trajectory the total NOX emitted is 1,519 kilograms. The flight time, for the NOX-optimized trajectory is 1,065 minutes while for the fuel-optimized trajectory is 995 minutes. Considering that the two cruise altitudes are the same for minimum NOX and fuel, in order to reduce the NOX emission the optimizer suggests flying at a lower speed than the fuel-optimized trajectory with an increment in the flight time. Figure 20 shows the flight path for the two optimized trajectories.
Considering that the time-optimized trajectory is exactly the same trajectory described in case one further consideration is required at this point. Regarding the NOX-optimized trajectory, it is interesting to notice that the optimizer suggests a solution where the aircraft flies at lowest and highest allowable Mach number and cruise altitude respectively. Highest altitude and lowest speed lead to minimize the engine thrust requirement. In turn, low thrust requirement means low TET, which results in low NOX emission.
In Figure 21 and Figure 22 shows the altitudes Mach number variation of the two climb trajectories against the flight distance.
It is evident how, similarly to the fuel-optimized trajectory, in order to minimize the NOX emission the optimizer suggests to reach the highest admissible altitude as faster as possible.
It is important to consider the fact that large amount of NOX is produced at TET values in the region of 1700 ~ 1800 K and it increases exponentially with TET. In this respect, the trajectory optimized for flight time produced a large amount of NOX. One of the main reasons for that, besides the fuel burnt, is the high value of TET required for the thrust. Considering only the cruise phase, the time-optimized trajectory emitted about 409 kilograms of more NOX respect to the NOX-optimized trajectory.
The multi-disciplinary optimization framework has been implemented in order to investigate the potential of greener trajectories as future possible solutions for the reduction of aircraft environmental impact. The optimization framework comprises three different simulation models: engine model, aircraft model and emissions prediction model and a GA based NSGAMO optimizer.
The multi-objectives optimization studies have been carried out in GATAC frame work focusing on minimization of conflicting objectives, such as fuel burnt versus flight time and NOX versus flight time for long range trajectories.
In the first optimization study a long-range mission of 14,195 kilometers has been considered. The results show a difference of 8.63% (79 min) in flight time and about 12.27% (14,790 kg) in fuel burnt between the fuel-optimized and time-optimized trajectories. In order to minimize the flight time the optimizer suggests a solution where the aircraft has to fly at minimum allowable altitude and maximum flight Mach number. On the other hand, the flight trajectory that minimized the fuel burnt is one in which the aircraft has to fly at maximum permissible altitude. The cruise Mach number that minimizes the fuel consumed does not correspond to the minimum allowed Mach number but it is a result of a compromise between fuel flow (power setting) and flight time.
Regarding the minimization of NOX emissions the results show that the aircraft has to fly at the highest allowable altitude and optimization is the minimization of NOX emissions the optimizer tends to reduce the power setting (TET) and all other aspects become secondary.
This preliminary application clearly shows the capabilities of GATAC framework as an optimization tool in obtaining optimum solutions at multidisciplinary level. However, more research efforts needed in enhancing the spectrum of the capability of the tool, for an example, use different optimizers with different objective functions; integration of different models such as
Noise, Lifing, & engine degradation etc. introducing practical ATM constrains and changing the current 2-D optimization to 3-D and 4-D.
In order to achieve the ACARE 2020 targets by reducing the impact of aviation on the environment in the short term, introduction of changes in aircraft operational procedures and rules under optimum trajectories is a promising solution. In conclusion, the implemented framework proved to be a valuable tool for identifying the characteristic features of aircraft trajectories with a minimum environmental impact and other operational consequences.
The research project has received funding from the European Union’s Seventh Framework Program (FP7/2007-2013) for the Clean Sky Joint Technology Initiative under grant agreement n0 CJSU-GAMSGO-2008-001. The authors are also grateful to EADS Innovation Works, Thales Avionics, Airbus France and the GSAF (Green Systems for Aircraft Foundation) members of the Technical University Delft (Faculty of Aeronautical Engineering), National Aerospace Laboratory NLR, and particularly Matthew Xuereb, Matthew Sammut and Kenneth Chircop of The University of Malta.