Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2016) Volume 5, Issue 4
New dry gas seal “DGS” groove geometry has been developed, using a verified three dimensional simulations. The effect of the various groove profiles; standard spiral, tapered-spiral, spiral with an annulus and tapered-spiral with an annulus were studied at wide range of operating speed. The results indicate that, tapered type spiral groove causes a reduction in opening force and in the leakage rate. In addition, increasing the taper angle reduces the temperature distribution inside the gas film and reduces the thermal stresses on the seal mating rings. The combined use of annuals and taper spiral groove decrease the leakage rate for spiral DGS with annular groove only. The final optimized spiral tapered seal with annuals reduces the leakage rate by 18.5% from standard seal, ensures uniform pressure distribution and hydrostatic lift at low speeds, resulting in low torque and reliable operating at start-up condition.
<Keywords: Spiral; Groove; Tapered; Annular; DGS; Performance
Dry Gas Seal (DGS) is considered one of non-contacting dynamic seal, which used for sealing leakage around rotating machines shafts. It has a lot of applications in natural gas and chemicals industry, it can be found in gas compressors and gas turbines as it has high operating stability and low maintenance cost [1]. The DGS is located on the compressor shaft sealing the flow inside the compressor from the external atmosphere. The seals are fed with a clean, heated, if necessary, and dry gas usually taken at the discharge of the compressor.
Many researchers have been working to understand the film flow dynamics inside DGS. Bing, et al. [2], presented a computational study for the effect of turbulence model on flow simulation in DGS. The effect of turbulence model has been ignored by DGS industrial designers. The velocity and pressure fields in the gas film and groove depth were predicted with direct numerical simulation (DNS) and Reynolds averaged Navier Stokes (RANS) methods. DNS method gives more accurate results than that predicted by RANS, which underestimated the calculated seal performance. Jing, et al. [3], developed a threedimensional numerical study for the micro-scale flow field in spiral groove DGS. The gas flow regime and film thickness were studied to explore their effect on the gas seal performance. Bing and Huiqiang [4] discussed the effect of micro scale flow field on spiral groove DGS performance in a numerical simulation based on corrected Reynolds equation. The results showed that the average pressure distribution in the gas film and the leakage rate are increased due to micro scale effects, which caused an increase in the seal opening force and significantly reduce the stiffness of the gas film.
Miller and Green [5] developed two new methods for calculating the flow properties between gas lubricated seal faces. The first method is mainly based on the step jump method; while the second one calculates the gas film frequency response using direct unsteady simulation of the pressure field for harmonic motion of the stator. The results from both methods agreed well with previously published results computed using the perturbation method. Peng et al. [6] developed empirical formulae for calculating the convection heat transfer coefficient of a stationary ring. However, Brunetiere and Modolo [7] reported that the range of validity of those empirical formulae was too small, especially when compared to Reynolds numbers observed during different mechanical face seal operations. Moreover, some parameters, such as material property and geometry of the face seal, were not considered in those empirical formulae.
Numerical simulation was conducted by Heshun, and Cichang [8], Five geometric parameters were investigated emphatically including groove depth, spiral angle, the ratio of groove width to the land width (circumferential), the ratio of dam length to the groove length (radial), and number of groove. To obtain more details about the fluid field and high stability of dry gas seal, Weibing, et al. [9] developed a simulation with Reynolds equation of compressible perfect gas, on isothermal condition, for T shape grooved dry seal. They investigated the effect of T shape geometrical parameters such as: groove depth, and balance clearance on the seal performance.
Kowalskik and Basu [10] described the analysis, design and testing of a spiral groove seal with reverse rotation capability. The spiral groove geometries were optimized for good forward rotational stiffness at design pressure and speed and acceptable reverse rotation capability at lower speed levels. The optimized parameters included number of grooves, groove angle, groove depth and land-to-groove width ratio. A comprehensive analysis method of simulating the complex thermo-flow in a dry gas seal was described by Hong, et al. [11] which was carried out by using the commercial computational fluid dynamics (CFD) software CFX [12]. The three-dimensional velocity and pressure fields in the gas film flow and the temperature distribution within the sealing rings were investigated for three kinds of film thickness. Thermohydrodynamic characteristics of the dry gas seal was studied for both air and helium as sealing gases. Qiu and Khonsari [13] developed a three-dimensional thermo hydrodynamic CFD model to study the characteristics of an inward pumping spiral groove mechanical seal pair. Based on their CFD model, a parametric study was conducted to evaluate the performance of the seal. They found that thermal behavior played an important role in the overall performance of a seal. Shahin, et al. [14] conducted a computational study on the reverse rotation effects on the spiral unidirectional dry gas seal performance and pressure distribution inside the gas film, also an investigation of using a different herringbone shape grooves configurations were performed to enhance the pumping action of the spiral grooves for DGS reverse rotation. The effect of tapering the spiral grooves in different directions was studied also by Shahin, et al. [15]. Three taper spiral grooves were studied each with three different angles, including taper grooves in the radial, circumferential and combined radial-circumferential directions. The results show that using taper grooves not only reduces the leakage rate but also reducing the seal opening force.
The above brief review reveals common shortcomings in existing studies in the literature. The studies were done for the standard design of the spiral groove dry gas seal with little attention to the thermo-flow analysis of the internal film at low speed and start up conditions. Little studies were performed to enhance the seal performance at these critical conditions. Ma et al. [16] investigated the thermo-hydrodynamic behaviors of standard spiral groove gas face seals. The thermal distortion on seal performance was analyzed. Only different operating conditions were studied such as working pressure and rotational speed, with no attention to the effect of seal face geometry. Experiments were conducted by Ding, et al. [17] to measure the temperature distribution in a dry gas seal. The tests were performed on spiral groove gas seal at different operating conditions such as, rotating speeds and pressures. A theoretical model was used to explore the temperature distribution in the gas film. The results obtained showed that isothermal model is compared with the thermal model but the sealing opening force and leakage flow were over predicted.
Furthermore, these studies did not consider adapting DGS to wide variety of rotational speed operating conditions; most of the modifications done are related to the spiral groove basic parameters. It is also noted that little studies are conducted to improve DRS start up conditions. Ochiai, et al. [18] optimized dry gas seal design for high speed and low minimum leakage. Different seal grooves were studied. The dynamic properties of a modified mechanical non-contacting seals were studied by Blasiak and Zahorulko [19]. Several seal face modifications such as micro-channels, compartments, micro-pores, texturing were studied numerically.
In the current study, a comprehensive analysis is proposed to resolve the effect of modifying the seal grooves geometry. Firstly, standard spiral groove DGS is modeled at different fluid state conditions and different rotation directions. Secondly, spiral groove DGS is modified by tapering the grooves, using annular grooves and tapered-spiral grooves with annular. For all studied cases, the internal flow and performance of the seal are analyzed and compared with the standard DGS.
Governing equations
All the numerical results presented in this paper were obtained by solving the three-dimensional; steady Reynolds-averaged Navier- Stokes equations. For absolute velocity formulation, the governing equations of fluid flow for a steadily moving frame may be written as follows [20]:
Mass conservation equation:
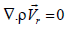 (1)
(1)
Momentum conservation equation (2):
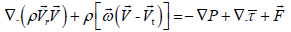 (2)
(2)
Energy conservation equation (3):
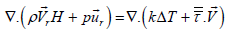 (3)
(3)
The numerical simulation has been performed with different fluid states, including laminar and turbulent states. The flow Reynolds number in the dry gas seal flow is calculated from eq. (4) as defined by [12]:
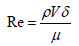 (4)
(4)
Under the flow conditions and dimensions indicated in Table 1, The Reynolds number is 1147 for δ=5μm, therefor the gas film flow is still laminar. However, many references show the importance of turbulence while simulating the flow in DGS. In the current study different turbulence models were investigated. The turbulent model is treated with non-equilibrium near wall treatments, with 2% turbulence intensity at flow inlet, which is compared with Large Eddy Simulation (LES). Second order discretization scheme is chosen for better accuracy. The solution residuals for continuity, momentum and energy equations have been set to be less than 10e-4. The seal performance parameters including leakage rate are monitored during solution to confirm its convergence (Table 1).
| Geometrical Parameter | Value | Operating Parameter | Value |
|---|---|---|---|
| Inner radius mm | 58.42 | Film depth (μm) | 3.05 |
| Outer radius mm | 77.78 | Sealing medium pressure (bar) | 45.852 |
| Groove root radius mm | 69 | Environmental medium pressure (bar) | 1.013 |
| Spiral angel (°) | 15 | Spin speed (rpm) | 10 380 |
| Ratio of groove to land | 1 | Inlet Temperature (K) | 300 |
| Grooves number | 12 | Dynamics viscosity kg/ (m. s) | 1.95 E–5 |
| Film Fluid | Ideal Air | ||
| Density ρ1 (kg/m3) | 54.1 | ||
| Specific heat Cp (J/kg. K) | 1072 |
Table 1: Calculation conditions of [11] for validation of the numerical method.
The fluid is treated as an ideal gas [4], the equation of state [5] is:
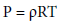 (5)
(5)
The Knudsen number is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale; it is commonly used to distinguish the flow micro effect and calculated from eq. [6]:
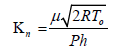 (6)
(6)
According to Ruan [21] the flow in the present study can be treated as a continuous medium because Kn = 0.002 which is less than 0.01 in the gas film, even for the smallest film thickness h=2 μm.
A uniform temperature of 300 K is assumed on the inflow boundary. Adiabatic wall boundary conditions are used for rotating and stationary walls, by specifying a zero heat flux at seal faces. The heat transfer through the seal rings and housing are neglected as performed by [3] and [8]. As we are modeling a problem that involves heat transfer, the viscosity is defined as a function of temperature. Sutherland’s viscosity law is used, in which the viscosity resulted from a kinetic theory by Sutherland [22-25] using an idealized intermolecular-force potential. The formula is specified using two coefficients as in eq. [7]:
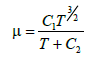 (7)
(7)
Convergence criteria
In order to ensure the solution convergence, the calculated residuals of the continuity equation, the three momentum equations, and the turbulence model equations are decreased to be 1e-4. In addition, the mass flow rate and static pressure at film fluid inlet and outlet were monitored during the calculation, by which we will be sure that it numerical errors reached a stable value. Four thousand iterations were developed for each case and it was found to be sufficient to satisfy the convergence criteria in the majority of cases.
Numerical boundary conditions
The sealing gas static pressure and turbulence properties were used at the domain inlet. The static pressure was used to set the outlet boundary condition. The single rotating reference frame model is used to model the fluid rotation. The model is used to simulate the fluid between the rotating and stationary faces of the dry gas seal. Figure 1 shows the basic geometrical parameters of the simulated domain and the spiral groove profile used. The computational domain and the hexahedral generated mesh are shown in Figure 2 in which the fluid domain is magnified by 1000 times in the groove depth direction for geometry and grid detail clarity only. The calculations are done without any scaling to capture the actual gas film properties between the seal faces. The sealing medium pressure is used at the inlet for the fluid as inlet boundary condition, the environmental medium pressure is used at the domain outlet as outlet boundary conditions, the rotating periodicity boundary condition is used and the wall boundary conditions with no slip velocity are employed at the stationary and rotating seal faces Ruan [21] (Figures 1 and 2).
To illustrate the effect of rotating ring groove geometry on the hydrodynamics and performance of spiral groove DGS, four groove types are studied as shown in Figure 3. The standard spiral groove, tapered spiral grooves, spiral groove with annular and tapered spiral groove with annular are all studied at the same film thickness and operating conditions. To examine the effect of using radial taper groove on the gas seal performance, the simulation is conducted for the gas seal with the same geometrical parameters except that the groove depth is decreased in the radial direction by taper ratio “TR=hr/h”. Four cases are studied with ratios TR=hr/h= 1, 0.75, 0.5 and 0.25. Smaller ratios of the groove depth ratio decrease the groove height at the gross. Annular groove is introduced in between the groove and land regions of the seal ring. Also taper spiral grooves with annular are also examined with ratios TR=hr/h= 1, 0.75, 0.5 and 0.25. The computational domains for annular and tapered annular cases are also shown in Figure 4. The simulation is also conducted at rotational speed rang from zero to 10380 rpm in the normal and reverse rotation directions (Figures 3 and 4).
The model is validated with results of [21,22] for which the geometric and operating conditions are shown in Table 1. These geometrical parameters are used for the present study, and then modified according to the studied parameters. In order to ensure the accuracy of numerical solution, a careful check for grid independence is conducted. Three; 1.17, 1.8 and 2.173 million computational nodes are used. The average processing time for different mesh is presented in Table 2. The pressure along the radial direction is plotted in Figure 5a. For present simulation with the three mesh densities and the results of [22]. The present results with 1.17 million agree well with data from [17], which agrees also with the spiral groove DGS pumping theory. No significant change is noticed by using thee higher mesh densities, so the grid with 1.17 million cells is used for all cases conducted in the present simulation. The present CFD results is also compared with Hong et al [11] for the same seal geometry and operating conditions as shown in Figure 5b. A good agreement between our present CFD results and CFD results of [11], but his model is slightly under estimate the pressure distribution especially near the groove step and at the begin of the land region (Figure 5 and Table 2).
| Mesh | Number of nodes | Average processing time Hours |
|---|---|---|
| Mesh 1 | 1.17 × 106 | 22 |
| Mesh 2 | 1.8 × 106 | 36 |
| Mesh 3 | 2.17 3 × 106 | 43 |
Table 2: Average processing time for different mesh.
Standard spiral groove gas seal
The influence of fluid regime is done by simulating the flow as a laminar flow and as turbulent flow using different turbulence model. The pressure along the radial direction is plotted in Figure 6 for laminar and turbulent flow calculations. The Laminar flow results agree well with data from literature [22], whereas the solutions of the turbulent flow using K-ε turbulence model or large eddy simulation are less accurate. The gas film pressure from turbulent calculations are over estimated, this is clear especially at the spiral groove gross. This is because that by using turbulence models, medium gas will be a viscous fluid, and in fact, gas is sticky and this is agreed with [3]. Which will make the calculated pressure at turbulent state is inevitable higher than the calculated pressure at laminar state. Based on this result, the laminar flow calculations are considered for all the studies conducted in the later sections (Figure 6).
The internal flow analysis is conducted and shown in Figure 7 for the static pressure, velocity and temperature at four angular positions shown in Figure 4a; 3.75°, 11.25°, 18.75° and 26.25°. The relation between the dimensionless static pressure, with respect to inlet gas pressure, and the dimensionless radial direction position is shown in Figure 7a; the static pressure is increased at the inner dam, which indicates the effect of the pumping action of the spiral groove. Static pressure maximum values are observed for the angular positions through the spiral groove θ=11.25°, near the dam, but with values lower than that at θ=3.75°, slightly after the groove boundaries. The pressure is developed through the spiral groove area with the direction of rotation. The pressure distribution over the land region at θ=26.25°, which located before of the groove, is quietly uniform when compared with other circumferential positions, the pressure change is minimal as compared with that plotted at the land region after the groove (Figure 7).
Figure 7b illustrates how the velocity magnitude normalized by rotating face speed at outer diameter, by rotating face tip speed is varied in the radial direction. The flow is decelerated through the groove circumferential positions and the highest velocity is predicted at the mid groove. The severe increase in velocity observed for positions θ=11.25°, θ=18.75° near the groove end occurs near the pressure peak at which the film fluid is accelerated rapidly to get out from the spiral groove. The land regions circumferential positions θ=3.75°and θ=26.25°, have more uniform velocity distribution. The gas exit at the seal inner diameter expanded quickly and reaches the atmospheric pressure, which results in a rapid acceleration of the flow in this region and a rapid increase in flow velocity moving away from the seal inner diameter. Many studies from literature [23] indicate the possibility of choked flow in DGS. The Flow inside DGS become supercritical flow, when the exit velocity is sonic and the pressure at the throat of the seal zone discharge is greater than the downstream pressure, which is normally atmospheric. To check the possibility of choked flow, the Mach number at the seal exit is monitored while simulation. At all the operating points in this study, the flow does not choke and the highest calculated velocity at the discharge did not reach the sonic condition. The normalized temperature distribution, by the inlet temperature, along the radial direction is shown in Figure 7c. Generally, a temperature increase is noticed with the flow from the outer to inner diameter at all circumferential positions. This temperature increase has its highest value in the dam area after the groove for positions at θ=11.25°, and θ=18.75°. As the flow enters the groove, a large amount of heat is transferred through heat convection resulting in low fluid temperature. However, at the inner portion of the groove, there is only a small amount of fluid exchange between the groove and the fluid film reducing heat transfer due to convection which results in a higher temperature at the end of the groove [24-26].
Influence of tapering the spiral groove
For evaluating the influence of tapering the spiral groove, the static pressure in the radial direction is plotted for different taper ratio as shown in Figure 8a, the radial taper groove has an effect on the pressure distribution in radial direction, as the taper angle increase the pressure distribution decreases and the pressure peak decreases. The pressure peak decreases as the inner dam height is reduced for lower taper ratios, which cause the pumping action of the spiral groove to be even smaller. Figure 8b shows the velocity distribution at θ=11.25° for the different taper ratios. The trend of the velocity distribution is the same for all taper ratios, but the sudden increase in the velocity at the dam inlet diameter is decreased as the tapper angle increased, which indicating that the flow will be more smooth for lower taper ratio (Figure 8).
Figure 8c shows the effect of radial taper groove angle on the temperature distribution. It is clear that the temperature decreases with increasing the taper angle especially at the groove end and seal dam area. This is due to the fluid exchange between the groove and the fluid film on top of the grooves. At higher groove tapered angle, the area of the groove contact with the gas system is larger, and the fluid exchange between the groove and the fluid film becomes greater, consequently heat is then transferred due to convection. Also the heat generated due to friction is reduced as the flow moves smoothly in the tapered grooves especially at the grooves end resulting in a lower fluid and seal temperatures. Figure 9a illustrates the effect of the groove taper angle and speed on the seal opening force. At lower groove taper angle, the opening force is higher and as the groove taper angle increases, the opening force decreases rapidly. The leakage rate also decreases with increasing the taper groove angle as shown in Figure 9b. This indicates that low leakage rate and low seal temperature are achievable, with high angle taper groove. On the other hand, if low wear is preferred, then groove without taper or small tapper grooves should be applied (Figure 9).
Influence of using spiral grooves with annular and tapered spiral groove with annular groove
In order to enhance the opening force of tapered DGS, an inner annular groove is presented at the end of the spiral groove. Peng Xudong et al. [26] studied numerically the effect of using an inner annular groove on the DGS performance. Different taper ratios are studied for the case with annular. The performance parameters for annular– taper DGS are shown in Figure 10, the use of annular seal increases the opening force with 5.6% at the design speed, and it gives also the maximum opening force at static conditions with an increase of 6.5% from the standard DGS. However, using annular seal will increase the leakage rate by 22.5% for the standard spiral seal. The increase of leakage rate results from the reduction of the dam extent, which increases the average clearance of the face seal as the seal dam covers less of the face area as noted by Zirkelback [24]. For decreasing the leakage rate, the grooves are tapered in the radial direction with ratios hr/h= 1, 0.75, 0.5 and 0.25. It is noticed that by decreasing the taper ratio, the leakage rate is decreased from 22.5% from the standard spiral seal to be 12% at full speed, but also the opening force will be decreased with the decreasing of the taper ratio. The annular-taper spiral groove DGS has high opening force at lowers speeds and low-pressure hydrostatic lift. Under static conditions, the annular taper spiral groove allows the film fluid pressure to break through the seal face. A uniform pressure distribution is resulted from the circumferential annular groove after the dam. The combination of these design features provides extra hydrostatic lift at static conditions, resulting in low start up torque (Figure 10).
In the following sections, the flow physics in the mid film are presented to indicate the performance properties discussed previously. The static pressure distribution on mid film plane is shown in Figure 11. For standard spiral, spiral with taper, spiral with annular and spiral with tapered annular grooves. The pumping action of the standard spiral is maximum for all cases, but the annular-taper groove reduces the pumping action of the spiral groove as revealed by the pressure increase near the inner dam. Although the annular taper spiral groove gives lower pumping effect, but it gives higher opening force more than that generated by standard spiral groove, this results from the increase in high pressure “43 to 46 bar” for annular and annular tapered spiral grooves. The average static pressure along the radial direction “Mid film” is shown at Figure 12a; the pressure peaks are located at the inner dam for the standard and taper grooves. The Annular and annular taper grooves generate lower pressure than standard one, but bigger area with high pressure is generated on the seal faces. The Average radial velocity along a mid-film plan is drawn in Figure 12b; higher radial velocities are predicted for the annular and annular taper cases with a noticed increase just after the annular ring. This also indicates the cause of increased leakage rate for seal face with annular grooves. The average static temperature along the radial direction is also shown in Figure 12c. The temperature is increased from the outer diameter till the dam inlet radius, resulting from the increase in static pressure due to the pumping action of the spiral groove. It is also noticed that the annular grooves have decreased the temperature distribution especially at the land after the spiral groove. Surface average temperature decreased from 335 K to 315 K, is expected to improve the working stability of seal to some extent. In order to evaluate the effect of groove geometry on the film fluid behavior, the velocity stream lines with vectors are drawn at mid film and mid of the groove depth is shown in Figures 13a and 13b respectively. However, a spiral groove seal develops some hydrostatic stiffness due to the step effect of the grooves in the radial direction. The hydrodynamic film stiffness has two components. The first one is due to the inward pumping action; the second component is due to the step slider bearing effect because of the presence of the alternate land and groove in the circumferential direction [24].
The velocity vectors indicate the effect of groove step on the flow direction. For the standard design, the flow on the groove area is directed to the circumferential direction and higher hydrostatic pressure is developed from the same case but with tapered groove, which resulting from the decrease in step height. The impact of the fluid particles with the groove step is increased by using annular groove, and more flow is directed in the circumferential direction, and consequently a high pressure is developed on an area larger than the standard design, which results in a higher opening force. The use of annular –taper groove causes a reduction on the effect of the groove step and lower hydrostatic pressure is developed and a reduction on the opening force is resulted from the case with annular groove only (Figures 11-13).
Optimized spiral tapered groove seal with annuals
In this section the optimized spiral tapered groove seal with annuals is compared with the standard seal for the same dam length ratio “DLR”. DLR is defined as the ratio between the dam length and the dam length for the standard seal. The annular tapper groove seal “TR 0.75” with DLR=0.63 and 1are compared with the standard seal in Figure 14, for normal and reverse operation direction. The seal open force is increased for seal with tapper annular grooves, with higher increase in the open force for DLR=1. The leakage rate for annular taper seal with TR=0.75 and DLR=1 is decreased by average 18.5% from the standard seal, the improvement in leakage rate detected over all the examined speed range and rotation direction. The increase of DLR from 0.63 to 1causes higher resistance for film fluid in the dam region and lower leakage rate is resulted (Figure 14).
In order to enhance the performance of spiral groove DGS, a three dimensional CFD model is developed to study the complex thermo flow in a DGS with different seal rotating face geometries. Standard spiral groove, spiral groove with radial taper, spiral groove with annular ring and finally a spiral groove with combined annular and taper groove are all studied at a constant film thickness. The model is validated with different number of computational nodes. The internal flow field and performance parameters for standard and modified seal face geometries are presented and discussed. The following conclusions can be made:
1. The numerical model based on Laminar flow simulation can predict the DGS performance and internal flow reasonably. The turbulent flow model over predict the developed static pressure along the seal faces.
2. The taper spiral groove will cause a reduction in the seal open force and leakage rate, the leakage rate is decreased as the taper angle decreased. Higher taper ratio as the groove taper angle increases the pressure. However, increase the taper angle causes significant decrease in the temperature distribution inside the seal.
3. The spiral groove with annuals causes a reduction in the pumping action of the spiral groove and increases the leakage rate resulting from the decrease in the dam extent.
4. The combined use of tapered spiral groove and annuals will enhance the seal performance especially for TR=0.75 and provide higher opening force at extremely low speeds. The leakage rate for the final optimized seal face is reduced by 18.5% from the standard seal along wide range of rotational speed.