Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2013) Volume 2, Issue 3
An analysis of a frequency measurement by rational approximations principle application in Aerospace Industry is introduced. The results obtained from a circuit simulation that implements the novel method previously mentioned for measurement are presented. Also, it is shown that the method can be implemented in affordable hardware.
<Keywords: Aerospace industry; Frequency measurement; Frequency domain sensors (FDS)
The measurement process for many physical variables is based on its conversion to frequency. Frequency Domain Sensors (FDS) are able to accomplish this task. If a physical parameter is converted to frequency, it can achieve a faster and more accurate measurement. Embedded in automobiles, robotic systems, aerospace crafts, and many other modern devices, FDS are increasing the quality of the measurement while they still needing better frequency measurement and registration methods. Many frequency measurement techniques have been proposed [1], most of them are based on the counting of the number of complete cycles that exists during a fixed time interval, the time is determined by the counter’s time base. This technique can be named as the classical method.
Other techniques are based on reciprocal counting and continuous time stamping. Another technique is one based on frequency measurement by pulse coincidence principle [2], it has been widely proved in the literature and shows to have a very good performance at high frequencies, according to the fundamental laws of Number Theory, it is accepted that this measurement method is insensitive to jitter [3].
There are many industrial applications of frequency measurement techniques and frequency domain analysis of electromechanical systems, for instance, Montmeat developed a quartz-crystal microbalance based on mass conversion into frequency of a quartz-crystal self-oscillation [4]. A wireless sensor interrogator that is capable to wireless detection and tracking of the resonant frequency of a passive inductor-capacitor circuit was proposed by Peterson et al. [5].
In Kulahet al. [6] shows that generator up-converts low-frequency environmental vibration to higher frequency through a mechanical frequency up-converter for most applications is used. As it is shown, there is a lot previous work using FDS, however there is no enough special research of the novel methods which permits fast and accurate at the same time frequency measurement.
Currently, most FDS are using DFT (discrete Fourier transform) of the signal spectrum, or even more classic methods, i.e. events per second count. The main advantages of resonant sensors over other kind of sensors are their stability, high resolution and quasi-digital output, among others; also they require a counter to measure frequency. In [7,8] get focused in Surface Acoustic Wave (SAW) sensors, in present work will experiment with another principle of FDS.
Our method [1] has good properties that lead us to the conclusion: method of rational approximations by mediants based on coincidences principle is the strongest tool for fast and exact measurements in short time intervals.
In the principle of rational approximation, a desired frequency is measured by comparing it with a standard frequency. The zero crossings of both frequencies are detected, and a narrow pulse is generated at each crossing [2]. As shown on Figure 1, the comparison for coincidence of both narrow pulses trains (yellow and blue tracks of screenshot) generates irregular independent narrow pulse train (Figure 1). This comparison is made using an AND-gate.
In Figure 1 Sx and S0 are the unknown and standard trains of narrow pulses, with frequencies fx and f0, and periods 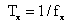 and
and 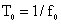 respectively.
respectively.  and
and  are integer numbers and represent the amount of whole periods between start and stop events. The pulses widths in both trains are t. The first, complete coincidece will be designated with zero indexes. This pair of pulses works as a trigger to start the frequency measurment. Pn y Qn are the numbers of counted pulses from Sx and S0 sequences that occur between adjacent coincidences. In [1,9] using
are integer numbers and represent the amount of whole periods between start and stop events. The pulses widths in both trains are t. The first, complete coincidece will be designated with zero indexes. This pair of pulses works as a trigger to start the frequency measurment. Pn y Qn are the numbers of counted pulses from Sx and S0 sequences that occur between adjacent coincidences. In [1,9] using
number theory is proved that the frequency can be determined by 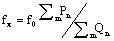 From Figure 1 if
From Figure 1 if 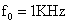 it can be calculated
it can be calculated 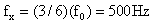 this can be corroborated by the oscilloscope’s medition (standard reference) parameters. Coincidence detector works as follows: pulsed signals with frequencies fx and f0 inputs into three &-gates. After first coincidence in gate &1 the trigger Tr prevents gate &2 and &3 from being active. The counters P y Q keep a count of the pulses of both frequencies until counter P recieves a results in the form of
this can be corroborated by the oscilloscope’s medition (standard reference) parameters. Coincidence detector works as follows: pulsed signals with frequencies fx and f0 inputs into three &-gates. After first coincidence in gate &1 the trigger Tr prevents gate &2 and &3 from being active. The counters P y Q keep a count of the pulses of both frequencies until counter P recieves a results in the form of 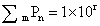
A block diagram of a frequency measurement device is shown on Figure 2 (more detailed design of circuit in [6]); based on this circuit was designed for simulation in the software Proteus Design Suite Release 8.0 SP1. The circuit was designed to be able to obtain fast and accurate frequency measurements with affordable cuircuits. The coincidence detector is based on a S-R Flip-Flop build with TTL Logic-Gates, the counters blocks are based on the 4 bit digital counter 74F393, the memory contains the circuits 62256 that are 32,768-word × 8-bit High Speed CMOS Static RAM and the procesor (MP) is build on Atmel’s SAM3X8E ARM Cortex-M3 CPU.
The standard and desired pulse trains are applied to circuit inputs for their count, and the measurement of the desired frequency is obtained by multipliyng the known standard frequency by the ratio between the desired count and the standard count obtained by two ditigal counters Q (counting number of 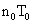 events) and P (the same for
events) and P (the same for 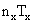 ).
).
In aerospace industry it is critical for many control and security systems to get fast and accurate physical variables measurements. Sensors as the ones provided by Digiquartz Pressure Transducers (Figure 3) have been used for decades in Flight Applications [10] including air data computers, missile testing, engine pressure ratio transmitters, and digital electronic engine control systems. Ground applications uses such sensors in wind tunnel instrumentation, air data test sets, and Altimeter Setting Indicators. These high resolution transducers are NIST Traceable-ISO 9001:2000 Quality System, also are the key sensors in an extremely accurate fuel measurement gauging system on geosynchronous communication satellites. The Model 760- 16B is the standard field calibrator used by the FAA to test airport altimeter systems.
The outputs from Digiquartz pressure transducers are two square wave signals whose period is proportional to applied pressure and internal transducer temperature. The Intelligent electronics measures these signals using a technique similar to that of a common laboratory frequency counter. Frequency output transducers can be connected to an intelligent electronic card to make a system capable of RS-232 and RS-485 operation.
The minimum time required to obtain a measurement is about 0.001 seconds, this implies that according to Table 1 this measurement device requires at least 30 cycles of the sensor’s frequency output to be able to measure 0 PSI and 41 cycles to determine 15 PSI. So, due to the necessity of averaging, this device finally can’t utilize all fastness of sensible part (last column of Table 1) due to non-optimal way of internal data processing.
| Input (PSI) | Output (kHz) | Output (s) | |
|---|---|---|---|
| Min | 0 | 30 | 0.000033 |
| Max | 15 | 42 | 0.000024 |
Table 1: Series 2000 Digiquartz pressure sensor´s parameters.
In order to register value of the sensor output it is needed to apply a signal conditioning. In this process the sensor’s output must be adjusted in a more convenient way for the measuring device functioning, the objective is to obtain a pulse width in the measured signal near (approximately equal) to the pulse width in the known frequency. It is shown on Figure 4 the simulation of our method functioning performed at the low and top boundary frequencies (3rd column of Table 1) of the considered sensor of Figure 3. In Figure 4a the comparison trough an AND-gate of the sensor’s output signal Sx and a signal with a known frequency S0 at 50 kHz is observed.
Also it is shown on Figure 4a the sensor’s output is at 0 PSI and in 4b the sensor’s output is at 15 PSI. The pulses widths in both trains are 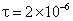 seconds. The pulse coincidence train is shown (rose track). The aim of such simulation is to prove the efficiency of our method for this real commercial sensor and an improvement in the measurement parameters can be obtained. From Figure 4a it can be easily calculated
seconds. The pulse coincidence train is shown (rose track). The aim of such simulation is to prove the efficiency of our method for this real commercial sensor and an improvement in the measurement parameters can be obtained. From Figure 4a it can be easily calculated  the same calculation is done for Figure 4b where
the same calculation is done for Figure 4b where  In the first case is possible to obtain the value of fx in 3 of its cycles or 1×10-4 seconds and in the second case the unknown frequency calculation lasts 5 of its cycles or 1.19×10-4 seconds.
In the first case is possible to obtain the value of fx in 3 of its cycles or 1×10-4 seconds and in the second case the unknown frequency calculation lasts 5 of its cycles or 1.19×10-4 seconds.
The required time to obtain a measurement (MT) of the physical parameter is given by the following expression:
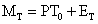 (1)
(1)
Where P is the number of cycles of S0 that exists before of the next coincidence, ET is the execution time in the microcontroller required to calculate the minimum operations, such as the P/Q division and its multiplication by the known frequency, also it is needed the conversion of the obtained frequency value to the measured physical parameter. For the proposed microcontroller it requires 633 and 12 clock cycles to calculate a division and a multiplication respectively, ET=0.000015351 seconds. For this particular sensor it requires 0.000075351 seconds to obtain a measurement when the sensor’s frequency output is 30 KHz and 0.00001153551 seconds when the sensor’s output is at 41.6 KHz
In any of the mentioned cases it is possible to obtain the physical variable measurement in a faster and accurate way than the commercial devices that are sold with the sensor, where the shortest measurement period is 0.001 seconds with a low measurement quality. As it is clear evident, the worst time of measurement using our method 0.000075351 s is still 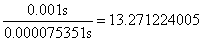 times faster than the time of parameter measurement of original commercial sensor.
times faster than the time of parameter measurement of original commercial sensor.
It was shown a frequency measurement process based on a functional circuit simulation, using commercial and affordable electronic components. This circuit allows obtaining a measurement with better quality (speed, accuracy) than the one provided by the sensor’s manufacturer. This optimized measurement is able to improve the control and security systems in the aerospace industry (i.e. airplanes).