Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2013) Volume 2, Issue 4
The present work aims at studying a new concept of a vertical tailless aircraft provided with a morphing tail solution with the purpose of eliminating the drag and weight created by the vertical tail structure. The solution consists on a rotary horizontal tail with independent left and right halves to serve as control surfaces. Different static scenarios are studied for different tail configurations. The proposed morphing configurations are analyzed in terms of static and dynamic stability and compared with a conventional configuration. The stability derivatives defining the limits of static stability are calculated for the whole range of tail rotation angles. The aircraft’s dynamic model is developed and feedback control systems are implemented. A sideslip suppression system, a heading control system and a speed and altitude hold system are studied for three different configurations, MC1, MC2 and MC3 configurations. Static results show that the aircraft is longitudinally stable for a wide range of tail rotation angles. Variation of tail dihedral and rotation angles are two mechanisms able to maintain directional and lateral stability but only the last is able to produce lateral force and yawing moment. Dynamic stability results demonstrate no spiral nor Dutch-roll modes due to the absence of the vertical stabilizer. The increase in tail rotation produces an appearance of the spiral mode and an unstable Dutch-roll mode that quickly degenerates into two unstable real roots with the increase in tail rotation. The addition of dihedral to the tail increases the stability of the overall modes while decreasing their variation amplitude with the tail rotation. The morphing tail configuration proved to be a feasible control solution to implement in an aircraft such as a small UAV, with the MC1 configuration being the most simple of the three morphing configurations and also the most reliable one.
<Keywords: Morphing aircraft; Vertical tailless aircraft; Tail rotation mechanism; Tail dihedral change mechanism; Automatic flight control system
In the field of aeronautics, shape morphing has been used to identify those aircraft that undergo substantial geometrical changes in their external shape to enhance or adapt to their mission profiles during flight. This creates superior system capabilities not possible without morphing shape changes. The objective of morphing concepts is to develop high performance aircraft with lifting surfaces designed to change shape and performance substantially during flight to create a multiple-regime, aerodynamically efficient, and shape-changing aircraft. Compared to conventional aircraft, morphing aircraft become more competitive as the demand for improved cost efficient aircraft increases.
The concept of implementing shape morphing in aircraft isn’t new. In fact, the use of retractable flaps or slats for increased lift during takeoff and landing, retractable landing gear for reduced drag during flight, variable sweep wings in fighters to reduce shock waves in transition from subsonic to supersonic speeds and variable incidence noses, as used in the Concorde for better pilot visibility during take-off and landing, are just a few examples of morphing solutions that aircraft have been using in the past [1]. However, recent research in smart materials and adaptive structures led to the development of new flexible skins and improved structural mechanization allowing substantial shape changes, particularly in wing area and twist and in airfoil camber, directly benefiting the airplane efficiency in each mission while expanding its overall flight envelope [2,3].
There are many challenges in the design of morphing aircraft: the integrity of structures needs to be ensured, the system should be designed so the required actuation force is realizable, the skin has to be designed to give a smooth aerodynamic surface while supporting the aerodynamic loads, the design process should be extended to encompass multiple flight regimes, engines need to be designed for efficient low and high speed operation, and control systems have to be designed with highly coupled control effects in mind. While many questions remain unanswered regarding the utility of morphing air vehicles, enough evidence of improved performance and new abilities has been established to warrant further consideration of the prospects of morphing aircraft, both for multiple flight regimes and for flight control [4].
The most common configuration of an aircraft used nowadays is built upon an empennage, or tail assembly, structure. Most aircraft feature empennage incorporating vertical and horizontal stabilizing surfaces which stabilize pitch and yaw, as well as housing control surfaces. Aircraft empennage designs vary with the number of tailplanes (stabilizers) and fins used and their location. Tailplanes can either have movable elevator surfaces or be single combined (stabilator or flying tail). There can also be alternative approaches as V and X tails and the case of tailless aircraft (flying wing) having all its horizontal and vertical control surfaces on its main wing surface.
Despite these different tail configurations, they all serve the purpose of providing an aircraft with pitch and yaw stability and control. The purpose of such a component in an aircraft mimics the one of a tail in birds. In fact, birds seem to adjust their tail to optimize their flight rather than just using them uniquely as a stabilizing and control surface [5]. Thomas studied the influence of bird tails on profile and induced drag. He concluded that by using the tail to generate lift, birds can have the small wings needed for fast flight (with the tail closed) and still have good performance in slow flight (with the tail spread), during turns, or when accelerating [5,6]. Evans et al. conducted wind tunnel tests on barn swallows and compared the results with deltawing theory (slender-wing theory). He observed that at low speeds, the tail was spred and held at a high angle of attack, and wingspan was maximized. At high airspeeds, the tail was furled; held parallel to the airflow and wingspan was reduced [7]. However, their empirical observations failed to provide robust support for the variable-geometry application of delta-wing theory.
Birds don’t have a vertical tail stabilizer and yet they are capable of controlling yaw motion. A study carried by Sachs revealed that, on one hand, bodies of birds are aerodynamically well integrated in the wing. The integration of the body is supported by its smaller size relative to the wing. As a consequence, the effect of the integrated body on the tendency to sideslip when yawing may be reduced when compared with a case where the body is considered alone without a wing. On the other hand, birds have a fast restoring capability in the yaw axis in terms of dynamic stiffness. This is due to the fact that the yawing moment of inertia is more reduced with a size decrease than the restoring aerodynamic moment, leading to a reduction in the required aerodynamic yawing moment in birds. This suggests that in such a case birds do not need a vertical tail as the wing alone can provide the required aerodynamic yawing moment [8].
A later study carried out by the same author regarding the specific tail effects on yaw stability in birds with different tail shapes revealed that elongated delta shaped tails can produce yawing moment in case of sideslip. This is due to the asymmetry in the airflow at the tail, because of the delta shape. This asymmetry leads to an asymmetrical lift distribution which also causes a correspondingly asymmetrical induced drag distribution forming a couple that yields a yawing moment [9]. The case of birds with forked tails was also studied and such tails showed drag forces at the elongated elements. By controlling the spread angle of each half tail, birds with such tails are able to control yaw due to the drag forces with different lever arms, forming a couple and hence a yawing moment. A further ability for producing stabilizing yawing moments is due to the legs and feet, according to Sachs. Depending on their length, they can stretch out in rearward direction to a considerably larger extent than the tail to control the couple produced by the asymmetry in drag produced by both feet. Sachs also suggests that as what happens with an aircraft flying at low speeds (take-off and landing situations), where flaps are used to increase drag, birds also lower their feet so that they are exposed to the airflow and generate drag for low speed flight conditions, while keeping them in a streamlined position for high speed flight, producing little drag.
The present work focuses on a new concept of morphing applied to the aircraft horizontal stabilizer with the purpose of eliminating the vertical component of the aircraft tail hence reducing weight and parasitic drag caused by the vertical stabilizer, while still maintaining the aircraft’s ability to control yaw. This is achieved by means of a rotary horizontal stabilizer that can generate horizontal forces when needed.
Starting from simple flight mechanics theory, the static aircraft body equations are assembled considering the aerodynamic loading of the wing and tail. The equations are kept non-linear for the tail angles as the tail rotation amplitude needed to provide trim and control is unknown. Different static scenarios are studied and the static stability of the aircraft is determined for different tail rotation and dihedral angles.
The chosen aircraft model is a Subsonic Business Jet Model (SBJ) from reference [10] that contains the majority of the aerodynamic derivatives needed, with the remaining ones being estimated. As the static model is built considering each one of the aircraft’s components, the aerodynamic derivatives that refer to the whole aircraft are not needed as they can easily be obtained from the assembled equations. Introducing dynamic stability and control theory, the aircraft’s dynamic model is developed followed by the implementation of the feedback control system that provides control for the aircraft’s tail. The dynamic model was also kept non-linearized but linear control techniques were used. Three different configurations are studied: the MC1 configuration, whith both halfs of the tail rotating together collinearly; the MC2 configuration with only one half rotating at a time, with the other one steady and the MC3 configuration with both halfs free to move independently.
The aerodynamic model of forces and moments acting on the aircraft, disregarding dynamic effects of the aircraft, was built by taking advantage of flight mechanics theory [11]. Four coordinate reference frames were defined: the Earth, wind, stability and body coordinate frames. Both Earth- Centered Inertial (ECI) and Aircraft-Body Coordinate (ABC) frames were of particular interest as they were used to write the aircraft equations of motion. These reference lines are depicted in Figure 1. To study the particular problem of a rotary horizontal tail, another coordinate system was introduced that has its x axis aligned with the aircraft body x axis and its y axis aligned with the horizontal tail span direction so it can rotate along with the tail, the Aircraft- Horizontal tail Coordinate (AHC) frame (Figure 1). The aerodynamic forces applied to the aircraft by each lifting surface, specified in the wind axes frame, were calculated and transferred to the aircraft-body reference frame.
Assembly of equations
The aircraft wind, stability and body axes are related with the wind velocity components by the aircraft’s angle of attack α and sideslip β. Following the rules for finding rotation matrices, the transformation from body to stability axes of the velocity vector Vbody specified in the body axes is
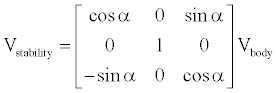 (1)
(1)
and the rotation from stability axes to wind axes is
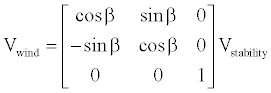 (2)
(2)
With these rotations defined by Sα and Sβ, respectively.
The rotation from wind to body axes can be calculated by inverting the rotation matrix as follows
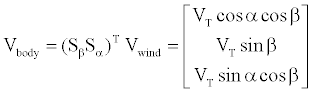 (3)
(3)
Considering the angle of incidence of the aircraft’s wing, the wing angle of attack is
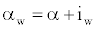 (4)
(4)
where iw is the aircraft’s wing angle of incidence.
The wing velocity vector can be determined by applying a rotation about the aircraft’s y axis to account for its incidence
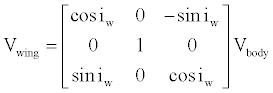 (5)
(5)
where the rotation matrix is defined as Sih.
The relation II.3 is now rewritten for the conventional horizontal tail as
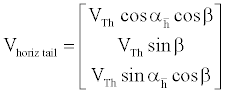 (6)
(6)
where 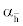 is the angle of attack of a conventional horizontal tail with no incidence angle.
is the angle of attack of a conventional horizontal tail with no incidence angle.
It’s now necessary to represent the velocity vector at the horizontal tail in the rotated tail surface by applying the same rotation rules as applied before. As the tail is usually built into the aircraft with an incidence angle we must also apply a second rotation to take this into consideration.
Figure 2 shows the rotations applied to transform from horizontal tail axes to a rotated tail axes as well as the rotation needed to account for the incidence angles of both wing and tail.
The transformation from the horizontal tail axes to rotated tail axes is
 (7)
(7)
And the rotation to account for the tail incidence is
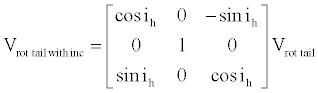 (8)
(8)
with these rotations defined by Sδh and Sih, respectively.
The complete rotation from horizontal tail to rotated tail axes including the tail incidence is
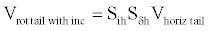 (9)
(9)
where δh is replaced by δhl for the left half horizontal tail and by δhr for the right half.
Considering small angles of attack and sidelip, the angles of attack for both left and right half tails are given by
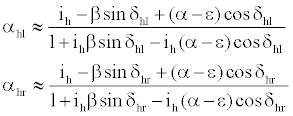 (10)
(10)
Having defined the wing and tail angles of attack, the aircraft body equations can be assembled. Trigonometric functions are written abbreviated.
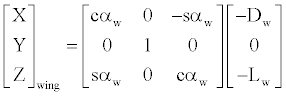 (11)
(11)
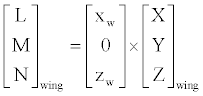 (12)
(12)
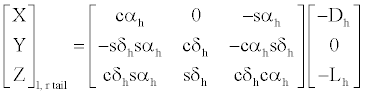 (13)
(13)
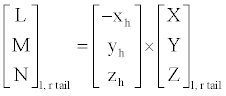 (14)
(14)
where the subscript h is replaced by hl for the left half tail and by hr for the right half, accordingly.
Angles of attack and elevators deflection angles to trim
For the case of zero tail dihedral and rotation angles, a trimmed longitudinal flight is obtained for αtrim=2.42 deg and δetrim=1.99 deg. As the tail rotates, the angle of attack to trim keeps constant and the elevators angle varies (Figure 3). The elevator behavior reverses with the increase in tail dihedral. As the dihedral angle increases the elevator angle to trim shows a larger variation throughout the entire range of tail rotation. The variation in dihedral angle also doesn’t change the angle of attack to trim. For a dihedral angle of about 30 deg the variation in elevators angle with the tail rotation angle is minimum for the range −45 deg 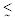 δh
δh 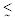 45 deg.
45 deg.
Variation of static stability with tail rotation and dihedral
The variation of the Cmα stability derivative was studied with both tail rotation and dihedral variation for a longitudinally trimmed flight. For each angle of tail rotation, the necessary elevator deflection was calculated.
It’s possible to observe in Figure 3b that although a longitudinally trimmed flight was always present for each tail rotation angle, the aircraft could only be static longitudinal stable for tail rotation angles in the range −67 deg 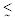 δh
δh 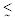 67 deg for the case of a tail with no dihedral. The addition of an initial dihedral angle greater than 30 deg maintains static longitudinal stability for the whole range of tail rotation angles.
67 deg for the case of a tail with no dihedral. The addition of an initial dihedral angle greater than 30 deg maintains static longitudinal stability for the whole range of tail rotation angles.
It is possible to observe from Figure 3c two mechanisms of increasing the value of Cβn: variation of tail rotation and variation of tail dihedral. Both mechanisms have the same purpose of increasing the aircraft wet and hence increasing its directional stability. The addition of an initial dihedral to the tail reduces the amplitude variation of Cβn: when using the tail rotation as a directional stability mechanism. The increase in tail dihedral angle produced an increase, in magnitude, in the value of Cβ1 (Figure 3d). Also, the variation of the tail rotation angle for a tail with no initial tail dihedral maintained a zero value of Cβ1. The addition of an initial dihedral to the tail contributed to the variation of Cβ1 with the tail rotation and hence the lateral stability was increased. However, the tail rotation mechanism was much less effective in producing lateral stability than the tail dihedral variation. When the tail was considered to be above the c.g. the value of Cβ1 proved to vary using the tail rotation mechanism with no initial dihedral and its effectiveness became similar to the dihedral variation mechanism.
Yawing moment produced by the tail rotation
Although the tail dihedral change mechanism was able to create the necessary directional and lateral stability, it was not able to to produce lateral force and yawing moment because when dihedral is changed the aircraft maintained its symmetry in the xz plane. However, the tail rotation mechanism, besides being able to produce directional and lateral stability, was also able to produce lateral force and yawing moment because when the tail rotated, asymmetries arise in aircraft’s xz plane.
Figure 4 depicts the variation of Cn with the tail rotation, for different tail dihedral angles, and also a comparison with a conventional configuration of horizontal and vertical tail with rudder. The yawing moment generated by a deflection of rudder was much more effective than a tail rotation. This happened because a longitudinal trim condition was being maintained by the elevators as the tail rotated and their deflection decreased the tail effectiveness.
The linear state-space model was built with the tail rotation nonlinearites included in the aircraft stability derivatives, as follows
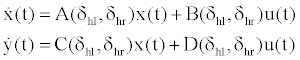 (15)
(15)
and the system eigenvalues were calculated as a function of the tail rotation angles.
Complete state-space roots
For the case of the rotary tail configuration, the system roots were calculated as a function of the tail rotation and dihedral angles. Figure 5 represents the roots calculated for the whole range of tail rotation for different tail dihedral configurations. Looking at the case of a tail with no dihedral (Figure 5a) the short-period roots became less stable as the tail increased its rotation angle. The phugoid poles kept stable for the whole range of rotation angles and eventually degenerated into two stable real roots with the increase in the tail rotation. As for the roll pole, it appeared to become more stable with the increase in tail rotation angle. No spiral nor Dutch-roll poles were present for zero tail rotation due to the absence of a vertical tail surface. The addition of tail rotation produced an appearance of an unstable spiral pole and two unstable complex poles, the Dutch-roll poles that quickly degenerated into two unstable real roots with the increase in tail rotation.
For the case of a tail with 10 deg of initial dihedral angle (Figure 5b), it is possible to observe that the two complex Dutch-roll roots exist, due to the presence of a vertical surface, but are unstable. These roots tended to stabilize for small rotation angles and destabilize for higher rotation angles and eventually degenerated into two unstable real poles. Again, the phugoid kept stable for the whole range of tail rotation and eventually degenerated into two stable real roots. As for the shortperiod and roll roots, their behavior was also the same as for the tail with no dihedral. The spiral pole was present and tended to destabilize with the increase of the tail rotation.
When a dihedral of 20 deg was initially added to the tail, the Dutchroll roots tended to stabilize whereas the phugoid ones became unstable very quickly, and were only stable for small angles of tail rotation, degeneration into two unstable real roots. Also, an interference with the Dutch-roll roots and the roll ones seemed to happen but both kept stable.
The addition of 30 deg of dihedral to the tail increased the overall stability of the modes while decreasing their variation amplitude with the tail rotation (Figures 5d to 5f). All the roots but the spiral kept stable for the whole range of tail rotation angles. The same happened when 45 deg of dihedral was initially added to the tail. The stability of the roll mode increased with the tail rotation for initial dihedral angles up to 30 deg. For higher initial dihedral values it decresead with the tail rotation, but its variation amplitude was also reduced. Nevertheless, it always kept stable.
Having determined the system stability characteristics, the possible control mechanisms using the tail were established and the feedback control laws for the closed-loop system were built.
The aircraft was considered to be in a steady cruise flight with no sideslip angle. The initial flight conditions used in the simulations are given in Table 1.
| Parameter | Variable | Value |
|---|---|---|
| Altitude | h0 | 9744m |
| Aircraft Speed |  |
[182 0 7.6] m/s |
| Components | ||
| Angle of attack | α0 | 2.42 deg |
| Pitch angle | θ0 | 2.42 deg |
| Elevators angle | δ0 | 1.99 deg |
| Thrust coefficient | CTo | 0.0295 deg |
Table 1: Initial flight conditions used for the simulations.
Stability augmentation
To understand the effect of the tail actuation on the augmentation of the system’s stability, the root-locus method was used to calculate the new system poles with the augmentation system added [12,13]. To be able to do that the system was linearized.
Furthermore, the contribution of the fuselage to the aircraft stability derivatives was added at this point. This was not done previously because the aircraft poles obtained from reference [10] did not include the fuselage contribution on the aircraft stability derivatives and so, for comparison purposes, this contribution was not taken into account. However, the absence of vertical wet area on the morphed aircraft configuration led to the disappearance of the Dutch- Roll and Spiral modes. This proved to be problematic when using the rootlocus method. Also, the fuselage contribution is of great importance to account for the effects of wind on the aircraft and to implement the necessary control, as described in section IV-E.
For the case of the longitudinal motion, the root-locus was evaluated for different feedback relations. The best solution proved to be the simultaneous feedback of the pitch rate q and the pitch angle θ to the elevators δe with feedback gains of kq=kθ=0.147. These values guaranteed level 1 flying qualities to both the short-period and phugoid modes (Table 2).
| Mode | Eigenvalue | ωn[rad/s] | ζ | Level |
|---|---|---|---|---|
| Short-period | -2.16 ± 3.67i | 4.260 | 0.507 | 1 |
| Phugoid | -0.057 ± 0.037i | 0.068 | 0.843 | 1 |
Table 2: Dynamic characteristics and flying qualities of the closed-loop linear longitudinal modes of both conventional and morphing configuration, for the SBJ aircraft.
For the case of the lateral motion, the best feedback solution proved to be the feedback of the yaw rate r to the rudder δr, for the case of the conventional configuration, and to the tail rotation δh, for the case of the morphing configuration, with feedback gains of kr=1.2 for the conventional configuration and kr=42.4 for the morphing configuration. These values guaranteed level 1 flying qualities to the Dutch-roll and roll modes. Despite the unstable spiral mode, its large time constant still guaranteed level 1 flying qualities (Table 3).
| Mode | Eigenvalue | ωn[rad/s] | T[s] | ζ | Level |
| Spiral | 0.003 | 0.003 | 336 | -1 | 1 |
| Dutch-roll | -3.7 ± 3.6i | 5.17 | - | 0.717 | 1 |
| Roll | -1.090 | 1.092 | 0.92 | 1 | 1 |
| (a) Conventional Configuration | |||||
| Mode | Eigenvalue | ωn[rad/s] | T[s] | ζ | Level |
| Spiral | 0.002 | 0.002 | 412 | -1 | 1 |
| Dutch-roll | -3.0 ± 2.7i | 4.010 | - | 0.749 | 1 |
| Roll | -1.090 | 1.092 | 0.92 | 1 | 1 |
| (b) Morphing tail configuration | |||||
Table 3: Dynamic characteristics and flying qualities of the closed-loop linear longitudinal modes of both conventional and morphing configuration, for the SBJ aircraft.
The foregoing results demonstrated that the rotary tail configuration was effective as a lateral augmentation system. The results are only valid for small rotation angles and don’t take into account the effect of the tail rotation in the elevators effectiveness. Also, the actuators dynamics are not taken into account and, for the case of the rotary tail configuration, the tail size is of great importance on the tail actuation time since rapid rotations of the tail may compromise its structural integrity.
The foregoing results demonstrated that the rotary tail configuration was effective as a lateral augmentation system. The results are only valid for small rotation angles and don’t take into account the effect of the tail rotation in the elevators effectiveness. Also, the actuators dynamics are not taken into account and, for the case of the rotary tail configuration, the tail size is of great importance on the tail actuation time since rapid rotations of the tail may compromise its structural integrity.
Control configurations
The attitude control systems tested consisted on a pitch and roll control and sideslip suppression systems while the flight path control systems tested consisted on a height and speed hold systems and also a heading and direction control systems [12].
The first morphing configuration considered (MC1) consisted on an aircraft with a rotary tail that can have a fixed dihedral angle. In this way, the control systems affecting pitch, altitude and speed were controlled using the elevators that rotate with the tail and the roll is controlled using the ailerons. The sideslip suppression and heading control systems were controlled using the tail rotation.
The second morphing configuration (MC2) consisted on an aircraft with independently rotary half tails that could also have a fixed initial dihedral angle between them. In this way, the roll was also controlled using the ailerons while the control systems affecting pitch, altitude and speed were controlled using one elevator from one half tail that doesn’t rotate. The other half tail rotated to provide the control needed for sideslip suppression and heading control systems. The half tail that rotated was chosen by the signal of the rate of yaw variable.
The third morphing configuration (MC3) also consisted on an aircraft with independently rotary half tails that could also have a fixed initial dihedral angle between them. The roll was again controlled using the ailerons but the control systems affecting pitch, altitude and speed were controlled using tail dihedral change. The sideslip suppression and heading control systems were controlled using the tail rotation.
These configurations were compared with the Conventional Configuration (CC) where pitch, altitude and speed were controlled using both elevators, roll was controlled using the ailerons and the sideslip suppression and heading control systems were controlled using the rudder deflection.
Figure 6 illustrates the different control configurations tested.
Sideslip suppression during a banked turn with pitch controller system
The direction control system used consisted on a roll control using the ailerons and a simultaneously sideslip suppression using the rudder, for the conventional configuration, and tail rotation, for the morphing configurations.
All configurations revealed similar times to complete the turn but the CC configuration was slightly faster than the remaining two and the MC2 slightly slower than the MC1 configuration. The pitch variation during the turn was minimal but again the CC configuration performed slightly better in controlling pitch than the remaining ones. The sideslip was effectively controlled by the rotary tail for either the MC1 or MC2 configurations but its maximum variation was higher than the CC configuration. This variation was only observable when the aircraft was entering and leaving the turn. Table 4 presents the maximum amplitude variation values of pitch and sideslip as well as the time to complete the turn for the two bank angles and different initial tail dihedral angles.
| Configuration | Maximum pitch θ variation | Maximum sideslip β variation | Time t to complete turn | ||||
|---|---|---|---|---|---|---|---|
| Γh | Фsat=30deg | Фsat=60deg | Фsat=30deg | Фsat=60deg | Фsat=30deg | Фsat=60deg | |
| MC1 | 0 deg | 0.22 deg | 0.87 deg | 2.13 deg | 4.26 deg | 273.7 s | 169.6 s |
| 15 deg | 0.12 deg | 0.46 deg | 1.51 deg | 2.93 deg | 272.1 s | 166.9 s | |
| 30 deg | 0.05 deg | 0.17 deg | 1.10 deg | 2.08 deg | 271.4 s | 167.0 s | |
| 45 deg | 0.01 deg | 0.03 deg | 0.84 deg | 1.55 deg | 271.4 s | 167.0 s | |
| MC2 | 0 deg | 0.25 deg | 0.74 deg | 2.56 deg | 4.17 deg | 276.2 s | 169.5 s |
| 15 deg | 0.09 deg | 0.39 deg | 1.38 deg | 3.07 deg | 272.8 s | 168.1 s | |
| 30 deg | 0.09 deg | 0.85 deg | 1.20 deg | 1.65 deg | 271.6 s | 167.1 s | |
| 45 deg | 0.10 deg | 0.19 deg | 0.92 deg | 1.71 deg | 271.4 s | 167.0 s | |
| CC | 0.00 deg | 0.00 deg | 0.36 deg | 0.67 deg | 270.9 s | 166.8 s | |
Table 4: Results of maximum pitch and sideslip variation values during a banked turn as well as the time to complete the turn, using sideslip suppression and pitch controller systems for MC1, MC2 and CC configurations.
The increase in the initial tail dihedral demonstrated an overall benefit in the aircraft during the turn: lower pitch and sideslip variation, shorter time to complete the turn and fewer requests to tail rotation (Figure 7).
The trajectory plot of Figure 8 shows no significant differences in the trajectory of the three different configurations with Γh=0 deg. It is evident the increase of approximately 200 m in altitude during the turn with фsat=30 deg and approximately 400 m for the turn with фsat=60 deg. The trajectory plots for the configurations with different initial dihedral angles are not illustrated but the results show no significant variation. The next control system discussed attempts to eliminate this altitude variation during the turn.
Sideslip suppression during a banked turn with altitude hold system
The second set of control systems tested was similar to the previous one but in this case the pitch control system was replaced by an altitude hold system. The altitude control using the MC2 configuration was difficult to implement due to the fact that the system was more oscillatory and so the yaw rate signal. As this signal served as the trigger to the half tail rotation, as described previously, the tail became prone to oscillations and eventually the system became uncontrollable. To overcome this problem, the MC2 configuration was modified so that the right half tail was left fixed and the left half provided the necessary rotation to control the sideslip, independently on the yaw rate signal. This modified configuration, described as MC2* configuration, was also used for heading control. All configurations revealed similar times to complete the turn. The altitude variation during the turn was minimal for the banked turn with фsat=30 deg and the CC configuration performed better than the remaining configurations. The altitude variation for the case of the banked turn with фsat=60 deg was slightly higher but also minimal, except for the MC3 configuration with initial tail dihedral angles of 30 deg and 45 deg. This happened because of the high initial tail dihedral angles which eventually caused the tail to reach its saturation limits and hence unable to keep the altitude within a reasonable range. Despite this, the MC3 configuration performed well with the remaining initial tail dihedral angles.
As what happened with the the previous set of control systems, the increase in the initial tail dihedral demonstrated an overall benefit in the aircraft during the turn, mainly in pitch and sideslip variations, diminishing their oscillation amplitudes.
Pitch and sideslip variations were also small for the MC3 configuration, performing better than the MC1 and MC2* configurations.
Despite the small variations in pitch and sideslip, the controller for the MC3 configurations was harder to tune and eventually the request to the tail was high and very oscillatory for the initial request. The MC1 and MC2* configurations were easier to control and demonstrated lower oscillation amplitudes. These results are depicted in Figure 9.
Table 5 presents the maximum amplitude variation values of altitude and sideslip as well as the time to complete the turn for the two bank angles and different initial tail dihedral angles.
| Configuration | Maximum altitude h variation | Maximum sideslip β variation | Time t to complete turn | ||||
|---|---|---|---|---|---|---|---|
| Γh | Фsat=30deg | Фsat=60deg | Фsat=30deg | Фsat=60deg | Фsat=30deg | Фsat=60deg | |
| MC1 | 0 deg | 3.78 m | 13.10 m | 2.28 deg | 5.91 deg | 273.3 s | 169.1 s |
| 15 deg | 2.38 m | 5.67 m | 1.46 deg | 2.97 deg | 271.6 s | 167.2 s | |
| 30 deg | 1.48 m | 5.21 m | 0.74 deg | 1.75 deg | 271.4 s | 167.0 s | |
| 45 deg | 0.63 m | 6.00 m | 0.58 deg | 1.53 deg | 271.0 s | 167.0 s | |
| MC2* | 0 deg | 4.95 m | 11.47 m | 3.86 deg | 7.30 deg | 280.1 s | 162.1 s |
| 15 deg | 2.20 m | 7.42 m | 0.69 deg | 1.10 deg | 268.7 s | 162.0 s | |
| 30 deg | 2.14 m | 5.46 m | 0.90 deg | 1.83 deg | 267.5 s | 161.8 s | |
| 45 deg | 1.47 m | 5.92 m | 0.72 deg | 1.21 deg | 269.6 s | 164.7 s | |
| MC3 | 0 deg | 7.28 m | 28.25 m | 1.57 deg | 2.28 deg | 271.5 s | 167.0 s |
| 15 deg | 8.70 m | 16.39 m | 1.34 deg | 2.06 deg | 271.4 s | 167.0 s | |
| 30 deg | 5.12 m | 98.45 m | 0.80 deg | 1.66 deg | 271.4 s | 167.0 s | |
| 45 deg | 4.87 m | 246.7 m | 0.83 deg | 1.46 deg | 271.4 s | 167.0 s | |
| CC | 0.44 m | 1.32 m | 0.39 deg | 0.66 deg | 271.5 s | 167.1 s | |
Table 5: Results of maximum altitude and sideslip variation values during a banked turn as well as the time to complete the turn, using sideslip suppression and pitch controller systems for the MC1, MC3 and CC configurations.
The trajectory plot of Figure 10 shows no significant differences in the trajectory of the four different configurations with Γh=0 deg. It is possible to observe that the altitude is maintained within reasonable limits for all four configurations. It is also evident that the aircraft does not maintain a constant radius of curvature because of the slight variation of sideslip during the turn.
Heading control system
A different kind of flight path controller tested was a heading controller together with a pitch and roll controllers. This system was tested under two different situations: first, the aircraft was set to follow a desired heading of 20 deg, controlling it with either the ruder (CC configuration) and tail rotation (MC1, MC2* and MC3 configurations); second, a lateral wind component of 10 m/s (19.4 knots) was introduced and the aircraft was forced to maintain the initial heading. The rudder and tail rotation were used, for the conventional and morphing configurations, respectively, to give the aircraft the required sideslip to overcome the lateral wind.
The results of both situations tested are displayed in Table 6. Regarding the results of the MC2* configuration some remarks must be pointed out. For the first situation of heading request, the addition of initial dihedral to the tail caused an increase in the sideslip value, as opposed to what happened so far. This was mainly due to the high saturation limits of the tail which created some negative dihedral values during some periods. These negative values of dihedral contributed to the increase of the sideslip variations. Also, an increase in the static error of the heading angle was observed for initial tail dihedral angles of 30 deg and 45 deg that could not be eliminated by tuning the controller gains. This is reflected in the time required to reach a constant heading which diminishes with the increase of initial tail dihedral.
| Configuration | Maximum sideslip β variation | Time t to reach constant heading | |||
|---|---|---|---|---|---|
| Γh | λ= 20 deg | λ = 0 deg hold with wind | λ =20 deg | λ = 0 deg hold with wind | |
| MC1 | 0 deg | 1.83 deg | 6.18 deg | 279.5 s | 108.9 s |
| 15 deg | 0.78 deg | 6.11 deg | 556.5 s | 180.3 s | |
| 30 deg | 0.21 deg | 6.03 deg | > 1000 s | 783.8 s | |
| 45 deg | 0.01 deg | 5.85 deg | > 1000 s | 903.7 s | |
| MC2* | 0 deg | 0.18 deg | 6.13 deg | 869.2 s | 498.2 s |
| 15 deg | 0.32 deg | 6.04 deg | 848.3 s | > 1000 s | |
| 30 deg | 0.40 deg | - | 580.4 s | - | |
| 45 deg | 0.46 deg | - | 407.5 s | - | |
| CC | 7.14 deg | 10.29 deg | 172.3 s | 103.3 s | |
Table 6: Results of maximum sideslip variation values for a heading request of 20 deg and a heading hold with lateral wind as well as the time to reach a constant heading value, using heading and pitch controllers for the MC1, MC2* and CC configurations.
For the second situation of heading hold with lateral wind, the MC2* tests were only possible to obtain with lower tail saturation limits of ± 30 deg so that only the first two MC2* configurations with lower initial tail dihedral values were possible to test. It was observed that the maximum sideslip variation values were similar to the ones of the MC1 configuration but the time to reach a constant heading value was much higher, approximately 500 s for Γh=0 deg and greater than 1000 s for Γh=15 deg.
The control input responses for the MC1, MC2*and CC configurations for both situations tested are plotted in Figures 11 and 12. A trajectory plot of both situations tested is illustrated in Figure 13 for the MC1 with Γh=0 deg, 15 deg and 30 deg and CC configurations.
Speed hold system
The last flight path control system tested was a speed hold system for the MC3 configuration, i.e. using the tail dihedral as a control of the longitudinal speed, for different initial tail dihedral angles. Two situations were tested, one with a tailwind component of 10 m/s and another with a headwind component of -10 m/s.
It is possible to observe from Table 7 that for the case of positive wind component (tailwind), the tail was only able to control the longitudinal speed when an initial dihedral angle of 45 deg was present. This happened because in order to be able to produce positive and negative variations in longitudinal velocity using dihedral change, one has to provide some initial dihedral to the tail.
| Configuration | Maximum speed u variation | Time t to reach constant speed | |||
|---|---|---|---|---|---|
| Γh | Tailwind of 10 m/s | Headwind of -10 m/s | Tailwind of 10 m/s | Headwind of -10 m/s | |
| MC1 | 0 deg | 5.75 m/s | - | > 200 s | |
| 15 deg | 3.49 m/s | - | 193.0 s | ||
| 30 deg | 2.43 m/s | - | > 200 s | ||
| 45 deg | 2.17 m/s | 1.39 m/s | 191.1 s | 121.8 s | |
| CC | 0.38 m/s | 0.42 m/s | 25.4 s | 25.5 s | |
Table 7: Results of maximum longitudinal speed variation values as well as the time to reach a constant speed for the MC3 configuration with a speed hold system.
Regarding the case of negative wind component (headwind), the tail was able to control the longitudinal speed regardless of the initial tail dihedral angle. The addition of dihedral proved to minimize the maximum speed variations and also reduced the time needed to reach a constant speed value. Nevertheless, these times were much higher than the one obtained with the conventional configuration.
Figure 14 depicts the tail input response for both cases of headwind and tailwind components. It is possible to observe that the dihedral request amplitude decreases with the increase in the initial tail dihedral but is much higher when compared with the request to the elevators.
The static results showed that the aircraft was longitudinal stable for tail rotation angles in the range −67 deg 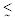 δh
δh 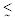 67 deg. Variation of tail dihedral angle and tail rotation angle are two mechanisms that were able to maintain directional and lateral stability but only the last was able to produce lateral force and yawing moment and its effectiveness was affected by the coupling with the elevators deflection.
67 deg. Variation of tail dihedral angle and tail rotation angle are two mechanisms that were able to maintain directional and lateral stability but only the last was able to produce lateral force and yawing moment and its effectiveness was affected by the coupling with the elevators deflection.
The dynamic stability results demonstrated no spiral nor Dutch-roll modes due to the absence of the vertical stabilizer. The increase in tail rotation produced an appearance of the spiral mode and an unstable Dutch-roll mode that quickly degenerated into two unstable real roots with the increase in tail rotation. The addition of dihedral to the tail increased the stability of the overall modes while decreasing their variation amplitude with the tail rotation.
A Stability Augmentation System (SAS) was implemented in a linearized model of the morphing aircraft so that the root-locus method could be used. Both longitudinal modes guaranteed level 1 flying qualities. The Dutch-roll and roll modes of the both configurations were stabilized and were level 1 in terms of flying qualities. Although the spiral kept unstable, its large time constant also guaranteed level 1 flying qualities.
From the control analysis results, the morphing tail configuration proved to be a feasible solution to implement in an aircraft such as a small UAV. The MC2 configuration proved to be problematic when used for heading control. The MC3 configuration demonstrated good results in all situations but the MC1 configuration was the most simple of the three morphing configurations and also the most reliable one. The addition of a dihedral component helped controlling sideslip and heading but increased the time needed to reach a steady state so that the choice of a tail dihedral angle must be a trade-off solution between the required maximum amplitude variation of the controlled variables and the desired time to reach a steady state in a given situation.
Future work will focus on implementing a non-linear control system, improve the model and redefine it to account for a bendable and torsional tail instead of a rigid one.