Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2022)
In order to study the possible occurrence of the ferroelectric-paraelectric phase transition in the monoclinic LiVO3, which remains experimentally ambiguous, we performed first-principles computations of the structural, dielectric and dynamical properties of LiVO3 in its high-temperature paraelectric structure of C2/c symmetry. The results show that LiVO3 exhibits three unstable phonon modes, which, after their condensation, lead to more stable phases of low symmetry. The obtained ground state phase is not ferroelectric, it is a non-polar phase of P21/c symmetry. However, the condensation of a low frequency mode obtained at 14 cm-1 leads to the ferroelectric phase of Cc symmetry, which confirms that the ferroelectric- paraelectric phase transition is possible for monoclinic LiVO3, which can then be controlled by applying an external parameter.
Pyroxene; DFT; Phonons; Phase transition; Oxide
LIBs: Lithium-Ion Batteries; EV: Electric Vehicles; HEV: Hybrid Electric Vehicles; DFT: Density Functional Theory; GGA: Generalized Gradient Approximation; ONCV: Optimized Norm- Conserving Vanderbilt pseudopotentials; DFPT: Density-Functional Perturbation Theory
The switchable macroscopic polarization characteristic of ABO3 type ferroelectric materials makes them good candidates for modern devices such as pyroelectric detectors, binary memories and electro-optic modulators for communication systems [1- 4]. The Lithium Vanadium (LiVO3) is one of these materials, widely used in the manufacturing of modern devices. It has been qualified to be used as solid electrolyte material as well as composite cathode for rechargeable Lithium-Ion Batteries (LIBs) used for Electric Vehicles (EV) and Hybrid Electric Vehicles (HEV) [5,6].
Due to the high mobility of Li+ cation, the unidimensionnal character of its structure and its electrochemical characteristics, LiVO3 appears as an important ferroelectric material which has been studied intensively in the past years [7-11]. LiVO3 belongs to the class of metavanadate pyroxenes family of the type MVO3 (M=Li, Na, K, Rb and Cs), in which infinite chains of corner shared VO4 tetrahedra, interconnected through MO6 octahedra. The experimental studies showed that LiVO3 must undergoes a ferroelectric-paraelectric phase transition at about 410°C from the Cc polar phase to the C2/c centrosymmetric phase [12,13].
By mean of high-resolution Neutron Powder Diffraction method, Muller, et al. [13], have associated this kind of phase transition to the reorientation of the anisotropic displacement ellipsoids of the lithium atoms around their average sites. This slight modification in structure introduced a symmetry problem in several experimental studies. Therefore, a detailed knowledge of ferroelectricity and phase transition mechanisms in LiVO3 is still remains obscure.
In the present work, we investigate the structural, dielectric and dynamical properties of monoclinic LiVO3, using first-principles methods. We study and discuss the possible occurrence of the C2/c-Cc ferroelectric phase transition. The condensation of the obtained phonon instabilities reveal that the P21/c phase, obtained from the condensation of the unstable Y2+ mode into the paraelectric C2/c phase, is the ground state phase. In addition, the condensation of the stable polar mode Γ2− into the paraelectric C2/c phase leads to the ferroelectric phase of Cc symmetry. This means that the ferroelectric phase transition remains possible for monoclinic LiVO3. Finely, the spontaneous polarization of such a ferroelectric phase is then calculated using two methods: The Berry phase formalism and from the knowledge of the born effective charge and the dielectric tensor.
Computational details
Our calculations were performed in the general framework of the Density Functional Theory (DFT) [14,15]. Using planewave pseudopotentials method as implemented in the ABINIT software package [16,17]. We chose the Generalized Gradient Approximation (GGA) [18], as exchange-correlation functional. Optimized Norm-Conserving Vanderbilt pseudopotentials (ONCV) were used to represent the core region of lithium, vanadium and oxygen atoms [19]. The V (3s 3p 3d), Li (2s) and O (2s 2p) levels, were considered as valence states in the generation of the pseudopotentials. Wave functions were extended in plane waves up to a kinetic energy cutoff of 45 Ha. The Brillouin zone was sampled with a 4 × 5 × 6 Monkhorst- Pack k-point grid converges the results very well [20]. We relaxed the structure until the remaining forces on the atoms are less than 10-5 Hartree/Bohr and the stresses on the unit cell are smaller than 10-7. Phonons frequencies, Born effective charges and dielectric tensors were computed using Density-Functional Perturbation Theory (DFPT) [21,22].
Structure
We first determined the structural parameters of the experimentally observed High-temperature paraelectric C2/c phase of LiVO3 by relaxing simultaneously the unit cell shape and the atomic positions. The C2/c structure has 40 atoms per conventional unit cell-or 20 atoms in the primitive unit cell. The crystal structure, as shown on Figure 1, exhibits the altering chains of VO4 tetrahedra (gray) and distorted LiO6 octahedra (blue). This structure consists of bands of V-O corner-shared tetrahedra run parallel to c-axis and is interconnected through edge-shared LiO6 octahedra which also run parallel to this axis. Our results after full structural optimization are listed on Table 1. Except of the typical error of the GGA method that is known to overestimate the lattice parameters, the results are in good agreement with the experiment.
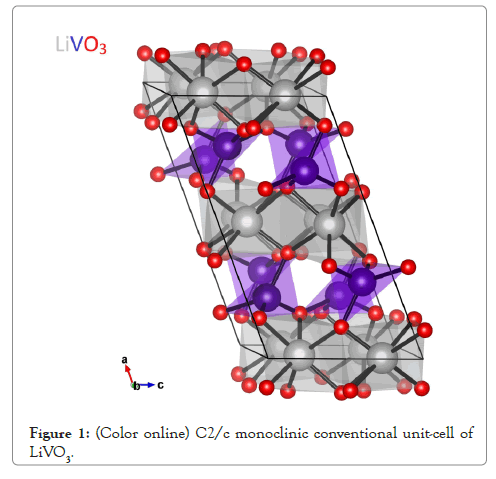
Figure 1: (Color online) C2/c monoclinic conventional unit-cell of LiVO3.
| Atom | Wyckoff | x | y | z |
|---|---|---|---|---|
| Li1 | 4e | 0 | 0.9148 | 0.25 |
| 0 | 0.9267 | 0.25 | ||
| Li2 | 4e | 0 | 0.2673 | 0.25 |
| 0 | 0.2831 | 0.25 | ||
| V | 8f | 0.2887 | 0.0933 | 0.2739 |
| 0.287 | 0.084 | 0.265 | ||
| O1 | 8f | 0.1159 | 0.1084 | 0.1689 |
| 0.1141 | 0.1112 | 0.166 | ||
| O2 | 8f | 0.352 | 0.2346 | 0.2894 |
| 0.3563 | 0.2723 | 0.2819 | ||
| O3 | 8f | 0.3582 | -0.0291 | 0.0857 |
| 0.3548 | -0.0276 | 0.0762 | ||
| a = 10.3348 Å b = 8.6362 Å c = 5.8897 Å β = 111.1900 (10.1616) (8.4281) (5.8863) (110.4660) |
||||
Table 1: Calculated lattice parameters and atomic positions of LiVO3 in the C2/c monoclinic phase. In parentheses are the experimental values reported here from [13].
Dielectric properties
The born effective charge (Z*) and the optical dielectric tensor (ε∞) are important and central for the parameterization of the LO-TO splitting that is considered as the contribution of the long range coulomb interactions to the lattice dynamics. These two quantities have been computed using linear-response techniques [22]. The elements of the calculated ε∞tensor are reported in Cartesian coordinates with the x and y axes aligned along the a and b directions of C2/c structure, respectively, and the z axis makes an angle of (β-π/2) with the c direction. Within this choice of Cartesian axes, the ε∞tensor is blocking diagonal in y and xz subspaces;
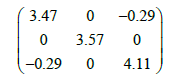
Neither experimental nor theoretical values to compare our results. It is well known that, for the dielectric tensor, the calculated values always overestimate the experimental one.
Table 2 shows the calculated Z* tensors for non-equivalents atoms. The Z* tensors are reported in Cartesian coordinates using the same set of axes as used for the dielectric tensor. The C2/c symmetry of LiVO3 requires that the Z* tensor should be anisotropic on each atom, so that the charge transfer takes place in different directions. Moreover, all the calculated Z* values are close to their corresponding nominal charges, which, contrast with what is observed for the class of ferroelectric perovskites that exhibit anomalous Z* [23].
| Atom | Z*xx | Z*xy | Z*xz | Z*yx | Z*yy | Z*yz | Z*zx | Z*zy | Z*zz |
|---|---|---|---|---|---|---|---|---|---|
| Li1 | 1.64 | 0 | 0.15 | 0 | 1.41 | 0 | 0.22 | 0 | 1.17 |
| Li2 | 1.5 | 0 | 0.26 | 0 | 1.17 | 0 | 0.22 | 0 | 1.06 |
| V | 3.14 | 0.2 | -0.72 | -0.09 | 3.4 | -0.64 | -0.76 | 0.26 | 4.71 |
| O1 | -1.23 | 0.59 | 1.09 | 0.77 | -1.5 | -1.68 | 1.03 | -1.23 | -3.82 |
| O2 | -2.4 | 0.32 | -0.53 | 0.14 | -0.94 | -0.02 | -0.48 | 0.24 | -1.08 |
| O3 | -1.08 | 0.73 | -0.03 | 0.83 | -2.23 | 0.21 | 0 | 0.03 | -0.93 |
Note: * Born effective charge.
Table 2: Born effective charges calculated for monoclinic LiVO3. The nominal charges of Li, V and O are +1, +5 and -2, respectively.
Dynamical properties
To study the structural instabilities in the monoclinic C2/c configuration of LiVO3, we performed zone-center phonon calculations in the conventional cell of 40 atoms (Figure 1). In this configuration the Brillouin zone is folding, and so gives access to phonons at Γ (0, 0, 0) and Y=(0, 1, 0) points. We obtained three unstable modes. The strongest unstable mode is at 61i cm-1 and corresponding to the irreductible representation . Γ2+ The two remaining unstable modes are at 57i cm-1 and 24i cm-1 and corresponding to the irreductible representation Y2+ and Y2− , respectively (Table 3).
| Γ2+ (61i) | Y2+(57i) | |||||
|---|---|---|---|---|---|---|
| Atom | x | y | z | X | y | z |
| Li1 | 0.0043 | 0 | 0.0367 | 0.0052 | 0 | -0.0263 |
| Li2 | -0.0314 | 0 | -0.1173 | 0.0043 | 0 | 0.1031 |
| V | -0.0058 | -0.0185 | 0.0003 | 0.0096 | 0.0206 | 0.0017 |
| O1 | -0.0072 | 0.0151 | -0.0015 | 0 | 0.0313 | -0.0041 |
| O2 | -0.0118 | -0.0122 | 0.0133 | 0.0124 | -0.0074 | 0.0021 |
| O3 | -0.0247 | -0.0267 | -0.0326 | 0.0275 | 0.027 | 0.0315 |
| Y2+ (24i) | Γ2-(14i) | |||||
| Atom | x | y | z | x | y | z |
| Li1 | 0.0179 | 0 | 0.0254 | 0.0027 | 0 | 0.088 |
| Li2 | 0.0087 | 0 | 0.0871 | 0.0396 | 0 | 0.1359 |
| V | -0.0056 | -0.0106 | -0.0096 | 0.0096 | -0.0011 | -0.0042 |
| O1 | 0.0051 | -0.0364 | 0.0247 | 0.0061 | -0.0048 | -0.0016 |
| O2 | -0.0019 | 0.0313 | -0.0058 | 0.0057 | 0.006 | -0.006 |
| O3 | 0.0031 | 0.0074 | 0.0483 | -0.002 | -0.0053 | -0.0352 |
Table 3: Calculated eigendisplacements (in a.u.) of unstable TO modes. Atomic displacements corresponding to polar mode Γ2- are also reported. The values in brackets present the frequencies of different modes in cm-1.
In order to study the symmetry-breaking behavior of C2/c
monoclinic LiVO3, we first individually condensed the three
unstable modes into the C2/c parent phase and then we
fully optimized the aroused distorted phases. We ported on Table 4 the low-symmetry phases with their corresponding
cell parameters obtained after full relaxation and their energy
differences (ΔEm) calculated with respect to the C2/c parent
structure. The condensation of mode
Γ2+ leads to a triclinic
structure of space group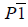 . While, the condensation of the
nonpolar modes
Y2+ and
Y2− lead to a monoclinic structure of space group P21/c. Also, the calculated ΔEm show that the
P21/c phase arising from the condensation of
Y2+ mode is the
most stable phase because it exhibits the lowest ΔEm, with an
important energy gain of about 150 meV/f.u. Significantly, as
shown on Table 4, the condensation of the stable polar mode
Γ2− into the C2/c paraelectric phase leads to a ferroelectric
phase of Cc symmetry. Despite numerous experimental efforts,
this phase transition is still ambiguously stated. This is probably
due to the very small structural changes between Cc and C2/c
phases [13].
. While, the condensation of the
nonpolar modes
Y2+ and
Y2− lead to a monoclinic structure of space group P21/c. Also, the calculated ΔEm show that the
P21/c phase arising from the condensation of
Y2+ mode is the
most stable phase because it exhibits the lowest ΔEm, with an
important energy gain of about 150 meV/f.u. Significantly, as
shown on Table 4, the condensation of the stable polar mode
Γ2− into the C2/c paraelectric phase leads to a ferroelectric
phase of Cc symmetry. Despite numerous experimental efforts,
this phase transition is still ambiguously stated. This is probably
due to the very small structural changes between Cc and C2/c
phases [13].
| Mode | Symmetry | Cell parameters | ΔEm |
|---|---|---|---|
| Γ2+ | 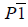 |
a=10.72, b=9.12, c =5.80 α=94, β=144, γ=81 |
-57.43 |
| Y2+ | P21/c | a=10.34, b=8.83, c=5.83 α=γ=90, β=114 |
-20.65 |
| Y2− | P21/c | a=11.12, b=11.76, c=5.64 α=γ=90, β=120 |
-20.65 |
| Γ2− | Cc | a=10.33, b=8.76, c=5.89 α=γ=90, β=110 |
-0.5 |
Table 4: Cell parameters (lengths in Å and angles in C°), energy differences ΔEm (in meV/f.u) and space groups of different phases obtained after condensation of unstable modes.
Spontaneous polarization
According to the modern theory of polarization [24], the spontaneous polarization of bulk LiVO3 is well attributed to a formal transformation from a paraelectric C2/c structure to a polar Cc structure. The Cc symmetry of LiVO3 allows a development of a spontaneous polarization along the x and z axes. To calculate this fundamental quantity we used both the Berry Phase approach (BP) [24], and from the knowledge of the born effective charges and atomic displacements as;
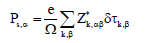
where Z*κ,αβ is the born effective charge tensor of atom k and δτκ,β presents the displacement of such atom along the direction β during the phase transition from the paraelectric C2/c phase to the ferroelectric Cc phase. This estimation gives 3.19 μC/cm2 along the x direction and 7.28 μC/cm2 along the z direction. From BF formalism, the computed spontaneous polarization is of 5.80 μC/cm2 and 7.56 μC/cm2 along the x and z directions, respectively. Finely, we observe that the Ps(Z*) underestimates Ps(BP) along the a direction, while along the c direction Ps(Z*) is in closer agreement with Ps(BF).
We have performed a systematical study of structural, dielectric and dynamical properties of LiVO3 in its high-temperature paraelectric structure of C2/c symmetry using density functional theory and density functional perturbation theory. We characterized the C2/c high-temperature structure. Dielectric properties and phonon frequencies were calculated. Unlike typical perovskites, the computed Z* are not anomalous and are close to their nominal values. A phonons calculation reveals three structural instabilities that lead after their condensation to more stable phases of monoclinic and triclinic symmetries. The ground state phase is monoclinic of P21/c symmetry. Finely, the condensation of the polar mode at 14 cm-1 leads to the polar phase of Cc symmetry, which confirms the possible occurrence of the ferroelectric-paraelectric phase transition.
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
Citation: Khedidji M (2022) First-Principles Study of Pyroxene Structure LiVO3. J Phys Chem Biophys. S1:003.
Received: 11-Feb-2022, Manuscript No. JPCB-22-15748; Editor assigned: 14-Feb-2022, Pre QC No. JPCB-22-15748 (PQ); Reviewed: 28-Feb-2022, QC No. JPCB-22-15748; Revised: 07-Mar-2022, Manuscript No. JPCB-22-15748 (R); Published: 14-Mar-2022 , DOI: 10.35248/2161-0398-22.S1.003
Copyright: © 2022 Khedidji M. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.