Journal of Osteoporosis and Physical Activity
Open Access
ISSN: 2329-9509
ISSN: 2329-9509
Research Article - (2016) Volume 4, Issue 4
Femoral osteochondroplasty is the most common treatment for femoroacetabular impingement (FAI). The risk of femoral neck fracture is increased following surgery and increases further when the bone is osteoporotic. The current requirement to undertake osteochondroplasty on patients with osteoporosis is forecast to increase; however, the effect of osteoporosis on the risk of post operative fracture is currently unknown.
We developed three three-dimensional (3D) finite element models using computerised tomography (CT) scan data for a hip with cam-type impingement and used them to investigate the association between osteoporosis and the increased possibility of femoral neck fracture after femoral osteochondroplasty.
Femoral osteochondroplasty was performed “virtually” on the intact hip model to two different resection depths, a ‘standard’ (6 mm) and a ‘critical’ resection (12 mm) depth, corresponding to 18% and 36% of the overall femoral neck diameter, respectively. Cortical and trabecular bone were included in the intact and resection hip models, and material properties representing both non-osteoporotic and osteoporotic cases employed, overall, 18 scenarios were analysed. Loading corresponding to “descending stairs” and “stumbling” activities were applied in the models enabling fracture propensity to be estimated.
Our model predicted that fracture propagation can occur in the bone of osteoporotic patients following osteochondroplasty during typical daily activities, such as descending stairs.
The level of damage increases significantly when patients are subjected to high load conditions and activities, even in non-osteoporotic patients, indicating an increased likelihood of fracture occurring. In the “stumbling activity” simulation, osteoporotic trabecular bone damage volume approached 50% for the 6 mm resection, rising to 70% at a resection depth of 12 mm. The corresponding rise in osteoporotic cortical bone volume damage was from 6% to 10%.
Our findings support the recommendation for protected weight-bearing in patients in the postoperative phase and suggest an extended period of protected weight-bearing in osteoporotic patients could be considered.
<Keywords: Femoroacetabular impingement; Osteoporosis; Osteochondroplasty; Finite element
FAI: Femoroacetabular Impingement; 3D: Three-Dimensional; CT: Computerised Tomography
Femoral osteochondroplasty is frequently performed as the surgical treatment for cam-type femoroacetabular impingement [1–4]. Postoperative femoral neck fracture is one of the recognized complications of this surgery [5–12] with incidence of rates between 0.8-1.0% [8,11,12]. Although femoral neck fracture is recognized as a potential post-operative complication of osteochondroplasty for FAI, little information is available as to what constitutes a safe depth of resection. To date, only two studies have attempted to provide some insight and guidance to this problem. An experimental cadaveric study [3] reported that at resection depths of 30% of the diameter of the femoral neck and greater, the energy required to produce fracture reduced significantly, causing a modification to the failure pattern. The results from a recent finite element study [5] suggested that resection depth should be kept to less than 1/3 of the diameter of the neck in order to ensure integrity of the femoral head and neck.
Hip fracture is considered to be one of the most serious potential consequences of osteoporosis [13–16]. Whilst it is acknowledged that bone quality is an important factor in addition to resection depth and the degree of post-operative weight bearing in femoral neck fractures following hip osteochondroplasty [7,10], the effect of osteoporosis on the risk of postoperative fracture is currently unknown. Since the older population are undertaking recreational and sporting activities with more physical requirements, the symptoms of cam FAI in older patients is likely to become more frequent [16–18]. Even though it is relatively uncommon to perform osteochondroplasty for FAI on older patients, it is sometimes appropriate and in addition, osteoporosis is being found increasingly in younger patients [17–20]. Recently, recommendations have suggested that bone mineral density scans should be considered in cases where osteopenia or osteoporosis is suspected in patients undergoing this type of surgery [10].
We developed three 3D finite element model using CT scan data from a patient with a cam-type femoroacetabular impingement and used these models to investigate the association between osteoporosis and both the mechanism and risk of femoral neck fracture after femoral osteochondroplasty. A quasi-brittle damage plasticity material formulation was employed in the Abaqus 6.10-1® FE analysis software (Abaqus, Inc., Dassault Systemes Simulia Corp, Providence, RI) to provide an in-depth evaluation of fracture risk.
In order to investigate the percentage of bone damage in osteoporotic bone following FAI and potential consequences for fracture, three 3D FE models were developed. An intact hip and 6 mm (18%) and 12 mm (36%) virtual resection models were created which enabled a study to be performed into cortical and trabecular bone damage when the models were subject to loading conditions corresponding to descending stairs” and “stumbling” activities. The study design for this work, which considered 18 scenarios, is illustrated in Figure 1.
A three dimensional finite element model was created using CT scan data from a patient with a prominent cam-type femoroacetabular impingement. The volumetric 3D CT scan data were imported into ScanIP® (Simpleware Ltd., Exeter, UK) enabling visualisation and segmentation of the bone geometries. The surface information available from ScanIP® was then exported to PowerSHAPE Pro (Delcam Plc, Birmingham, UK) enabling a solid model to be produced. The solid model was read into the Abaqus 6.10-1® FE analysis software (Abaqus, Inc., Dassault Systemes Simulia Corp, Providence, RI) for assembly, mesh generation and subsequent analysis. Further details of the geometric model generation process are available in Alonso-Rasgado et al. [5].
Two virtual resections were performed on the model, in the area identified by a surgeon (TB). The maximum impingement zone defined by the CT scans was considered to define the outer limits of the resection in both cases. One was a “normal” case of resection, considering only the sculpting of excess bone on the femoral headneck junction, resulting in a resection depth of 6 mm or 18% of the overall femoral neck diameter. The second resection was considered a “critical” case, performed to a depth of 12 mm or 36% of the neck diameter. Figure 2 illustrates the sequential process used to perform the virtual osteochondroplasty, beginning with the information obtained from the CT scans, the subsequent construction of the hip model and finally, the execution of the virtual resection.
Geometry
Three 3D finite element models of the proximal third of the femur were developed to analyze the two resection cases and the nonresection (intact) case. A solid model of the intact femoral head neck was created first. The shape of the resection area as defined by a surgeon (TB) was considered as the maximum extent of the impingement zone. The defined resection area identified was imported into Delcam PowerSHAPE Pro® (Delcam Plc, Birmingham, UK) where a “resection tool” was created to facilitate the creation of smooth resections and thus avoid the formation of irregular edges which can cause mesh irregularities and result in unrealistic stress concentrations when a structure is analysed. The resection area was extruded to create a solid model which was then imported into the Abaqus 6.10-1® FE analysis software where Boolean subtraction/intersection operations were performed on the intact femoral head-neck model to generate virtual resections to the required depths. Linear 4-noded tetrahedral elements were used to mesh the geometries [5].
Materials
It is widely recognized that the material properties of bone change with age. The elastic modulus of human femoral cortical bone has been reported to reduce by 1-2% per decade after 35 years of [21,22]. Similarly, trabecular bone mass starts to decrease between the ages of 20 and 40 by around 6-8% per decade [23]. A common approach used by researchers to simulate the effects of osteoporosis in numerical models of the femoral head neck is to reduce the elastic modulus of both the cortical and trabecular bone by a percentage compared to ‘normal’ values [24–26]. Dickenson et al. [27] obtained the mechanical properties of femoral cortical bone from normal subjects and subjects with osteoporosis. For the osteoporotic patients (average age 81 years) the average modulus of elasticity was determined to be around 32% less than the ‘normal’ value for a young adult. As a result of this, some researchers have reduced the elastic modulus by this percentage when simulating osteoporosis in the femur [24–26]. In order to simulate osteoporotic trabecular bone, a common approach has been to reduce the elastic modulus by 66% compared with non-osteoporotic, healthy bone [24-26]. This figure is arrived at by considering the loss of bone mass with age [23] and the empirical relationship established between apparent density and elastic modulus [28].
The model described in this paper assumes both cortical and trabecular bone to be brittle materials that exhibit isotropic, elasticplastic behaviour. The material formulation employed assumes a nonlinear stress-strain relation and considers the evaluation of fracture by employing the theory of isotropic damaged elasticity combined with isotropic tensile and compressive plasticity, to define a failure envelope that encompasses cracking in tension and crushing in compression.
The material damage plasticity for quasi-brittle materials such as bone, assumes tensile cracking and compressive crushing as the main failure mechanisms. These variables direct the propagation of yielded material and the decrement of the elastic stiffness [29]. The damage plasticity model represents the inelastic behaviour of the bone by combining isotropic damaged elasticity with isotropic tensile and compressive plasticity. It is used to describe irreversible damage that occurs during the fracture process and it assumes that the main two failure mechanisms are tensile cracking and compressive crushing. The evolution of the fracture is defined by the tensile and compressive plastic strains which define how the yielded material is spread after the ultimate strength is reached. Values for the density and elastic modulus for healthy, non-osteoporotic cortical and trabecular bone were taken from the literature [25,27,30–32]. Young’s modulus for osteoporotic bone was calculated by reducing the corresponding values of Young’s modulus for healthy cortical and trabecular bone by 32% and 66%, respectively. Densities were calculated using the following relationships, E = 2065 ρ 3.09 and E =1904 ρ1.64which have been determined for cortical and trabecular bone respectively [31]. Table 1 shows the values employed for the elastic material properties of cortical and trabecular bone for the healthy and osteoporotic cases [25,27,30,32]. Plastic properties were defined following a damage plasticity model based on the stress-strain curves for cortical and trabecular bone [33,34]. The stress-strain curves for healthy, nonosteoprotic bone were taken from the literature and osteoporotic bone curves were obtained by reducing the corresponding stress values by 32% for cortical and 66% for trabecular bone (Figure 3).
| Cortical bone | Trabecular bone | |||
|---|---|---|---|---|
| Healthy | Osteoporotic | Healthy | Osteoporotic | |
| Density, ρ [tonne/mm3] | 1.98e-9 | 1.75e-9 | 4.3e-10 | 2.2e-10 |
| Young’s modulus, E [MPa] | 17,000 | 11,560 | 477 | 162 |
| Poisson’s ratio | 0.3 | 0.3 | 0.3 | 0.3 |
Table 1: Elastic material properties for cortical and trabecular bones used in the model.
Cartilage was included in the model and assumed to exhibit elastic-plastic isotropic behaviour with property values taken from the literature [5,35].
Loading and boundary conditions
A section of the hemi-pelvis including the acetabulum was generated and inserted in the models to transmit the joint loads to the femoral head. A “Tie” constraint in Abaqus 6.10-1® was used to define the interaction between the femoral head and acetabulum, ensuring that adjacent nodes underwent the same displacement. In order to enable the effective transfer of the load to the femoral head whilst avoiding local stress concentrations, a “Rigid body” constraint was established on the hemi-pelvic bone [5]. The distal section of the proximal femoral segment was fixed in all directions for displacements and rotations.
Three loading scenarios were modelled. The “average peak load” and “high peak load” derived from the “descending stairs” activity were applied [36]. The “average peak load” corresponds to the forces acting in a subject of body weight of 750 N. The “high peak load” acts in a subject of body weight of 1000 N. The forces applied in the third loading case corresponded to those derived from the “stumbling” activity, calculated under the assumptions of the “high peak loading” scenario. Table 2 shows the component and resultant forces corresponding to the three loading cases considered in the models [36]. The loads were applied incrementally up to 100% of the resultant forces shown in Table 2.
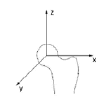 |
Peak contact forces | |||
| Activity | Resultant Force F [N] | Fx [N] | Fy [N] | Fz [N] |
| Descending stairs (Average) | 2000 | 370 | 292 | -1944 |
| Descending stairs (High) | 4200 | 776 | 613 | -1082 |
| Stumbling | 11000 | 2462 | 1523 | -10607 |
Table 2: Forces considered in the models.
Mesh sensitivity analysis and physical corroboration of the model
A mesh convergence analysis was undertaken in order to ensure accurate results could be obtained without requiring excessive computational resources. The analysis consisted of taking the intact, non-resection model and comparing the average von Mises stress in the femoral neck for three mesh densities: coarse, medium, and fine meshes, consisting of 79,000, 138,000 and 928,000 elements, respectively. The medium density mesh was chosen since the results changed by <0.5% between this and the fine mesh. Table 3 shows the number of elements employed in the three models, the intact (non– resection) and 6 and 12 mm resection models.
| Tetrahedral Elements | |||
|---|---|---|---|
| Model/Resection depth [mm] | Cortical | Trabecular | Total |
| 0 | 45,207 | 137,945 | 183,152 |
| 6 | 77,201 | 132,056 | 209,257 |
| 12 | 74,846 | 129,442 | 204,288 |
Table 3: Number of elements employed in the models.
Corroboration of the model was performed by comparing predictions with the experimental results from a cadaveric investigation that involved testing to fracture 15 pairs of human femurs [3]. The mean age of the cadaveric specimens was 79 years. We subjected our osteoporotic intact, non-resection model to loading and boundary conditions representative of those used in the cadaveric study and compared the neck stiffness with the mean neck stiffness of the control group from the experimental study [3]. Our model predicted a neck stiffness of 604 N/mm which compares favourably with that obtained from the cadaver study, which was 686 N/mm.
Measurements
The tensile and compressive damage output variables from the model refer to specific material degradation at the micromechanical level indicating that the bone has undergone permanent damage. Permanent material damage was taken as indicating the initiation of fracture in the models. The volume of bone damaged in tension and in compression was calculated for both cortical and trabecular bone in the femoral head-neck shaft region. In the results we concentrate on analysing the volume of bone damaged in tension as it is recognized that bone is weaker in tension than in compression [34,36–38].
Volume of bone damaged is the volume that exhibited stresses over the yield point of the material after being subjected to the loading conditions. Once the yield point is reached any deformation is irreversible and consequently, a failure in the material is immediate. An element is considered damaged once its stress value exceeds the ultimate strength for the material after being subjected to the loading conditions. The sum of the volume of the damaged elements corresponds to the volume of bone damaged. The results from the model indicate that no permanent material damage occurs at any resection depth in the trabecular and cortical bone in both the nonosteoporotic and osteoporotic cases for the “descending stairs” activity when subjected to “average peak loading (Table 4). However, when subjected to “high peak loading”, although no material damage was indicated in the cortical bone at any resection depth, material damage was registered at resection depths of 6 and 12 mm in the osteoporotic bone and at 12 mm in the non-osteoporotic trabecular bone indicating an increased likelihood of fracture occurring.
| % Bone Damaged | ||||
|---|---|---|---|---|
| DESCENDING STAIRS (AVERAGE LOAD 75 Kg) | ||||
| CORTICAL | TRABECULAR | |||
| HEALTHY | OSTEOPOROTIC | HEALTHY | OSTEOPOROTIC | |
| 00_RES (NON RESECTION) | 0% | 0% | 0% | 0% |
| 06_RES (6mm DEPTH) | 0% | 0% | 0% | 0% |
| 12_RES (12mm DEPTH) | 0% | 0% | 0% | 0% |
| % Bone Damaged | ||||
| DESCENDING STAIRS (HIGH PEAK LOAD 100 Kg) | ||||
| CORTICAL | TRABECULAR | |||
| HEALTHY | OSTEOPOROTIC | HEALTHY | OSTEOPOROTIC | |
| 00_RES (NON RESECTION) | 0% | 0% | 0% | 0% |
| 06_RES (6mm DEPTH) | 0% | 0% | 0% | 10% |
| 12_RES (12mm DEPTH) | 0% | 0% | 4% | 54% |
| % Bone Damaged | ||||
| STUMBLING (HIGH PEAK 100 Kg) | ||||
| CORTICAL | TRABECULAR | |||
| HEALTHY | OSTEOPOROTIC | HEALTHY | OSTEOPOROTIC | |
| 00_RES (NON RESECTION) | 0% | 5% | 6% | 34% |
| 06_RES (6mmDEPTH) | 0% | 6% | 44% | 49% |
| 12_RES (12mm DEPTH) | 0% | 10% | 70% | 71% |
Table 4: Percentage of bone damage for all the scenarios after full loading.
Figure 4 shows the damage volume in tension in non-osteoporotic and osteoporotic trabecular bone for the different resection depths in the “descending stairs” scenario for the “high peak loading” case. The results are shown at loading increments up to 100% of the applied load. It can be seen upon inspection of this figure that no material damage is present in the non-resection cases. In the case of the “normal” resection depth (6 mm), damage occurs in 10% of the osteoporotic trabecular bone volume at 100% of the “high peak load” but not in the non-osteoporotic, healthy trabecular bone. For the “critical” resection depth (12 mm), a level of material damage is recorded for both nonosteoporotic and osteoporotic trabecular bone. Damage occurs in approximately 4% of the non-osteoporotic trabecular bone when 100% of the “high peak load” is applied. In the osteoporotic case, 15% of the trabecular bone volume shows damage at around 60% of the “high peak load” rising sharply to 54% at full load. In the “stumbling” scenario damage was registered in both trabecular and cortical bone types. Figure 5a shows the volume damage in the cortical bone for the “stumbling” scenario. No material damage is indicated in the healthy, non-osteoporotic bone for all resection depths considered. However, a level of damage is present in the osteoporotic cortical bone at all resection depths, including the non-resection case. The volume of cortical bone damage is 5% at 100% loading for the non-resection scenario, rising to 6% and 10% for the “normal” and “critical” resection depths, respectively. Damage is initiated at around 82% of the full load in both resection cases and at approximately 92% load in the nonresection simulation.
In the trabecular bone for the “stumbling” scenario, damage was observed in both healthy and osteoporotic bone at all resection depths including the non-resection case, as can be seen in Figure 5b. In the non-resection scenario, 6% of the non-osteoporotic trabecular bone volume indicated material damage at 100% load compared to 34% for the osteoporotic bone case. The percentage of bone damage then increased with resection depth in both the non osteoprotic and osteoporotic trabecular bone scenarios. At a resection depth of 6 mm, the bone damage volume was 44% and 49% in healthy and osteoporotic trabecular bone respectively. The bone damage percentage at a resection depth of 12 mm was 70% for both non osteoporotic and osteoporotic trabecular bone. Figure 5b also indicates that damage starts to occur in the osteoporotic trabecular bone at lower loads than in the corresponding healthy, non-osteoporotic bone cases.
Analysis of the damage distribution pattern in the cortical osteoporotic bone of the proximal femur at a resection depth of 12 mm for the “stumbling” activity simulation suggests that damage will initiate in the resection area at around 80% of the loading (Figure 6).
As load increases further, damage expands over the resection area and transversely through to the posterior area of the femoral neck. A similar analysis in the trabecular bone indicates that damage initiates here in the inferior-medial area of the resection at 25% of the loading. Damage on the posterior surface of the neck is confined to a few small areas which start to appear at 90% load.
The results of the finite element analysis suggest that there is a risk of fracture in osteoporotic patients after femoral osteochondroplasty as indicated by the relatively large volumes of trabecular and cortical bone that our model predicts will undergo damage in the osteoporotic case. This risk extends to non-osteoporotic patients also when they are subjected to abnormally high loading.
The model predicted that no damage was present as a result of the “descending stairs” activity at any resection depth under “average peak loading”. However, under “high peak loading”, the model indicated that damage occurred, initiating in the trabecular bone of the femoral head-neck following osteochondroplasty. This damage was present in the 12 mm resection case in healthy, non-osteoporotic trabecular bone and in both the 6 mm and 12 mm cases for osteoporotic bone. At 6 mm resection depth, 10% of the osteoporotic trabecular bone volume has undergone permanent damage, indicating the possibility of microfractures in the internal structure of the bone. At 12 mm resection depth, the damage in the trabecular bone exceeds 50% signalling that internal fractures have become more significant.
The critical scenario occurred when osteoporotic bone was subjected to the loads developed in the “stumbling“ scenario, as the model predicted damage, suggesting the initiation of fracture, in both trabecular and cortical bone at all resection depths and also in the nonresection case. The volume of osteoporotic trabecular bone damage exceeded 30% in the non-resection case, rising to 70% at a resection depth of 12 mm. The corresponding rise in osteoporotic cortical bone volume damage was from 5% to 10%, which although a small percentage, is very significant since cortical bone is the outer most bone of the femur structure and has a higher stiffness, suggesting that once this bone is damaged, the risk of fracture is significantly increased.
The FE model developed in this study has several limitations which typically apply to all numerical analyses of this type [4]; in particular, we did not consider possible variations in the elastic modulus of trabecular bone due to loading direction, trabecular orientation, and anisotropy [39]. In addition the reduction in the thickness of the cortical bone as a result of osteoporosis was not considered [40].
However, research suggests that the error introduced by such assumptions should be relatively small when considering bone from a single anatomical site [39]. In addition, we did not investigate the effects of repeated or cyclic loading which may occur when a patient undertakes typical daily activities such as descending a flight of stairs, in which case fracture may occur at lower loading levels due to fatigue; or the reduction of bodyweight (loading conditions) as consequence of the decrease in the bone density.
In conclusion, our model predicts that damage can occur in the bone of osteoporotic patients following osteochondroplasty for camtype impingement during typical daily activities, such as descending stairs. The model predicted that the extent of bone damage was significantly greater for the osteoporotic scenario, for example osteoporotic trabecular bone damage volume was 34% for the intact hip scenario in the “stumbling activity”, compared to 6% for the healthy trabecular bone case; for cortical bone, damage was 8% in the osteoporotic case compared to 0% in the healthy case. For the 12 mm resection, osteoporotic bone damage volume increased to 71% and 10% for trabecular and cortical bone, respectively. These results suggest that it is important that the weight bearing in the post-operative phase should be strictly protected. Furthermore, the level of damage increases significantly when patients are subjected to high load conditions and activities suggesting that even greater protection is required for heavier patients and that great care should be taken to avoid the adverse loading conditions modelled. The methodology presented in this study is general and can be used to investigate the potential effect on bone integrity of ostechondroplasty.
The authors would like to thank the Consejo Nacional de Ciencia y Tecnologia (México) for supporting the postgraduate student involved in this work.