Advances in Automobile Engineering
Open Access
ISSN: 2167-7670
ISSN: 2167-7670
Research Article - (2016) Volume 5, Issue 2
A Multiple Model Adaptive Estimation (MMAE) based approach of fault diagnosis for Li-Ion battery is illustrated in this paper. Electrochemical modelling approach is integrated with MMAE for fault diagnosis. This real physics based model of Li-ion battery (with Li-Co-O2 cathode chemistry) with nominal model parameters is considered as the healthy battery model. Battery fault conditions such as aging, overcharge and over discharge causes significant variations of parameters from nominal values and can be considered as separate models. Output error injection based Partial Differential Algebraic Equation (PDAE) observers are used to generate the residual voltage signals. These residuals are then used in MMAE algorithm to detect the ongoing fault conditions of the battery. Simulation results show that the fault conditions can be detected and identified accurately which indicates the effectiveness of the proposed battery fault detection method.
<Keywords: Electrochemical model; Lithium-ion batteries; Particle swarm optimization; Parameter identification; Battery management system
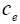 : Lithium ion concentration in the electrolyte phase.
: Lithium ion concentration in the electrolyte phase.
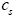 : Lithium ion concentration in the active materials in both electrodes.
: Lithium ion concentration in the active materials in both electrodes.
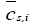 : Volume-averaged concentration of a single particle.
: Volume-averaged concentration of a single particle.
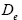 : Diffusivity at electrolyte phase.
: Diffusivity at electrolyte phase.
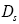 : Diffusivity at solid phase.
: Diffusivity at solid phase.
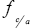 : Mean molar activity coefficient
: Mean molar activity coefficient
F : Faraday constant.
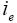 : Current in the electrolyte phase.
: Current in the electrolyte phase.
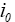 : Exchange current density.
: Exchange current density.
I : Load current.
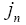 : Molar ion fluxes between the active materials in electrodes and the electrolyte.
: Molar ion fluxes between the active materials in electrodes and the electrolyte.
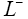 : Length of negative electrode.
: Length of negative electrode.
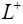 : Length of positive electrode.
: Length of positive electrode.
n : Number of active materials.
R : Universal gas constant.
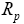 : Radius of the spherical particles.
: Radius of the spherical particles.
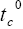 : Transference number.
: Transference number.
T : Average internal temperature.
U : Open circuit potential.
V : Cell voltage.
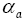 : Charge transfer coefficient in anode.
: Charge transfer coefficient in anode.
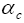 : Charge transfer coefficient in cathode.
: Charge transfer coefficient in cathode.
γ : Observer gain constant.
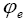 : Potential at electrolyte phase.
: Potential at electrolyte phase.
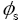 : Potential at solid phase.
: Potential at solid phase.
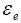 : Volume fraction at electrolyte phase.
: Volume fraction at electrolyte phase.
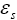 : Volume fraction at solid phase.
: Volume fraction at solid phase.
η : Over-potential for the reactions.
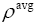 : Average density.
: Average density.
κ : Rate constant for the electrochemical reaction.
Amongst all the secondary (alternative) energy sources available for various applications such as Plug-In Hybrid Electric Vehicle (PHEV), Hybrid Electric Vehicle (HEV), Electric Vehicle (EV) and portable electronic devices such as smartphone and laptops, lithium-ion (Liion) battery is considered to be the most promising [1]. Compared to the other alternative options for energy sources (such as Nickel-metal hydride and Lithium iron phosphate etc.) lithium-ion batteries have some unique advantages including: these batteries have higher specific energy, have minimum memory effect, provide best energy- to-weight ratio, and have low self-discharge when idle [2,3]. Based on these stated advantages, Li-ion batteries is the leading candidate for the upcoming generation of aerospace, automotive, and other applications.
PHEV, EV and HEV have been gaining more acceptances in recent years due to their low emissions and better fuel efficiency [4]. Performance of these transportation options are significantly dependent on the electrochemical energy sources e.g. installed battery modules integrated with the vehicle powertrain. Depending on the user driving habit and the road conditions, battery undergoes through different operating conditions as the battery load demand changes. The safe operation of the entire battery module is always expected, as it is one of the most vital components of the stated vehicle configurations. But in reality, it is not always possible to maintain the desired safe and healthy operating conditions of the battery system for a number of reasons. For instance, battery can be overcharged during operation, can be over-discharged at different rates. Moreover, battery aging is another potential situation due to long time cycling of the battery.
For HEV, the on board Battery Management System (BMS) is responsible for managing the rechargeable battery system by monitoring its state of operation, protecting the battery from unsafe operating zone, and reporting the diagnostic data to the operator while managing the battery operation. To ensure the optimal operation of Li- Ion battery without sacrificing the stated advantageous features, fault condition monitoring is of critical importance. These fault conditions can cause serious negative impact on the battery operation and life if they are not detected and managed quickly.
Based on the usage of the battery and type of operations involved, a number of Fault Detection and Diagnosis (FDD) methodologies have been developed. All the model based FDD techniques make use of two major types of model, namely the equivalent circuit based models and true physics based models. In equivalent circuit based models, the battery is modelled by assuming that the true behaviour of the battery is attainable using a combination of voltage source, capacitors, resistors, and Warburg impedances. The circuit parameters of the stated components are experimentally determined, in which the insight into the real physics of the battery is ignored. This approach does not deal with the real dynamics of the battery chemistry.
On the other hand, the real physics based models, such as the one presented by Doyle, Fuller, and Newman [5] are primarily based on partial differential equations which contains all the required information regarding the true battery chemistry. This electrochemical model is based on the concentrated solution theory [6]. However this model is too complex to be used in a real time application. Model reduction via realistic simplifying assumption is used to overcome this issue. The work presented in this paper is based on the reduced order partial differential equation [1], representing the electrochemical battery model.
A large body of work exists that aims at the fault detection and diagnosis of rechargeable batteries. Adaptive estimation technique has been used in [7], which is based on equivalent circuit model. Extended Kalman Filter (EKF) was utilized to estimate the state variables of the non- linear battery model that was used in this paper. EKF is based on an approximation of Taylor series, which cannot deal with highly non-linear systems. Another shortcoming of this work is that, it did not consider one of the major variables in the battery system, i.e. temperature. An Adaptive Recurrent Neural Network (ARNN) for prediction of remaining useful life (RUL) was used in [8], which is also modelled based on equivalent circuits. Synthesized design of Luenberger Observer (LO) was adopted in [9], along with equivalent circuit model for fault isolation and estimation. The used observer works well with minimum or no measurement noise in the system. But this methodology does not perform well when significant measurement nose is present in the system.
Other major studies related to State of Health (SOH) and Remaining Useful Life (RUL) of Li Ion battery is based on data-driven methods. In [10], the data-driven method is presented on the diagnosis and prognosis of the battery health in an alternative powertrain. For estimation purposes, the authors used a Support Vector Machine (SVM) type machine learning technique. A similar methodology is adopted a conditional three-parameter capacity degradation model in [11]. Kozlowski [12] presented a battery parameter identification, estimation and prognosis methodology presented using several techniques, e.g. Neural Network (NN), Auto Regressive Moving Average (ARMA), Fuzzy Logic (FL) and Impedance Spectroscopy (IS) etc. Since the data- driven method is based on the relationship between input and output, the real physics of the battery model is ignored in this approach as is in ECM.
Multiple Model Adaptive Estimation (MMAE) is used in this work to detect the faults in a Li-ion battery. This adaptive estimation method requires representation of different fault scenarios, generate the residual signals and then to isolate the faults of different kinds using the algorithm. The generation of residuals and evaluation of them plays a vital role on the performance of the diagnosis [13]. In this work, the residuals are generated by comparing the simulated outputs of the fault models with the simulated output of the true plant model.
The work presented here aims at detecting several faults, i.e. aging, Over-Discharge (OD), and Over- Charge (OC) along with the detection of the healthy model. Among the stated fault scenarios in a Li-ion battery, OD and OC are critical for maintaining the health of the battery. While over-charging can lead to overheating that can lead to the vaporization of active material and explosion, over-discharge can short circuit the battery cell [14]. However, if these faults can be detected quickly according to the described methodology, steps can be taken to solve the issues before the faults can go to their extreme conditions.
This paper is organized as follows. Section 3 illustrates the battery electrochemical model used in this work. It is followed by the presentation of the reduced order model and PDAE observer equations. Section 5 describes the multiple model adaptive estimation technique. Section 6 discusses fault diagnosis method used in this work. Finally the findings are summarized in the conclusion section.
The electrochemical battery model captures the spatiotemporal dynamics of li-ion concentration, electrode potential in each phase, and the Butler-Volmer kinetics which governs the intercalation reactions [15]. A schematic of the model is provided in Figure 1.
In the provided geometry, the model considers the dynamics of Liion cell only in X -direction. Therefore, the model considered in this work is a 1- D spatial model where variations of the dynamics in Y and Z directions are assumed to be small. It is also assumed that Li-Ion particles are considered to be of spherical shapes with mean radius of Rp situated along X-axis [15].
In Figure 1, the main regions of the li-ion battery model are shown. The entire spatial length is divided into three regions, namely, negative electrode (ranges from 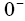 to
to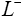 ), separator (ranges from L− to L+ ) and the positive electrode (ranges from L+ to L+ ). Two electrodes are separated by the thin and porous separator region through which only lithium ions ( Li+ ) can pass, i.e. the electrons must flow through the circuit outside the battery [16].
), separator (ranges from L− to L+ ) and the positive electrode (ranges from L+ to L+ ). Two electrodes are separated by the thin and porous separator region through which only lithium ions ( Li+ ) can pass, i.e. the electrons must flow through the circuit outside the battery [16].
The governing equations of the electrochemical model of the Li-ion battery are given by the following set of Partial Differential Algebraic Equations (PDAE) [1,3,5,6,15,17,18]:
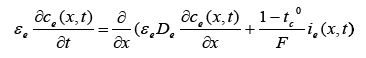 (1)
(1)
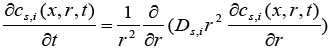 (2)
(2)
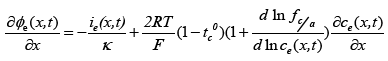 (3)
(3)
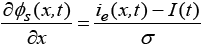 (4)
(4)
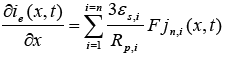 (5)
(5)
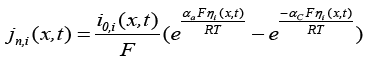 (6)
(6)
Here 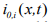 is the exchange current density and
is the exchange current density and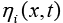 is the over-potential for the reactions, equations of which are [1]:
is the over-potential for the reactions, equations of which are [1]:
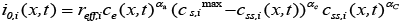 (7)
(7)
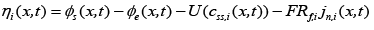 (8)
(8)
Here 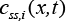 is the ith concentration at solid phase evaluated at
is the ith concentration at solid phase evaluated at 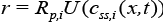 is the open circuit Potential of the ith active material in the solid phase and
is the open circuit Potential of the ith active material in the solid phase and 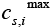 is the maximum possible concentration in the solid phase of the ith active material and this is a constant.
is the maximum possible concentration in the solid phase of the ith active material and this is a constant.
The cell temperature is considered to be lumped and was modeled based on the following equation [1]:
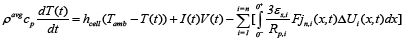 (9)
(9)
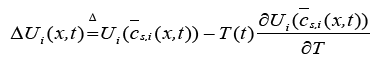 (10)
(10)
Here, 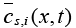 is the volume-averaged concentration of a single particle, which is again defined as:
is the volume-averaged concentration of a single particle, which is again defined as:
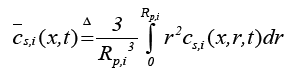 (11)
(11)
In the above equations 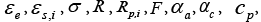
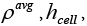 and
and 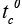 are all constant parameters while
are all constant parameters while 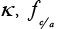 and
and 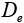 are dependent on electrolyte concentration and temperature and
are dependent on electrolyte concentration and temperature and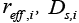 and
and 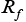 are Arrhenius-like parameters which follows the equation [1]:
are Arrhenius-like parameters which follows the equation [1]:
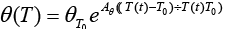 (12)
(12)
The open circuit potential for the positive electrode (cathode) is given by the following empirical equation [19]:
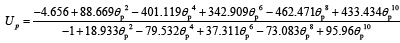 (13)
(13)
Where, 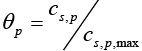 is a dimensionless number ranges from 0 to 1.
is a dimensionless number ranges from 0 to 1.
Similarly, the open circuit potential for the negative electrode (anode) is given by [19]:
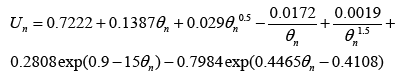 (14)
(14)
Where, 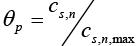 is also a dimensionless number ranges from 0 to 1.
is also a dimensionless number ranges from 0 to 1.
Output voltage of the battery model is then given by [1],
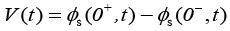
Due to the complexity of the stated PDAE model, the electrochemical model is reduced based on a few simplifying assumptions [1]. The intention of reduction is to build a model from the simulation point of view while maintaining the ability to capture all the cell dynamics [1]. The key assumption made here is that the electrolyte concentration is constant, i.e. 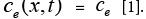 Another assumption is the introduction of an approximate solution of the diffusion equations in the solid active materials in each electrode as presented in [20]. Using these two assumptions, the reduced order PDAE equations can be presented as follows [1]:
Another assumption is the introduction of an approximate solution of the diffusion equations in the solid active materials in each electrode as presented in [20]. Using these two assumptions, the reduced order PDAE equations can be presented as follows [1]:
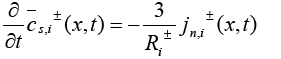 (16)
(16)
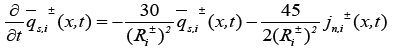 (17)
(17)
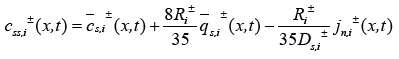 (18)
(18)
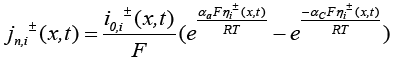 (19)
(19)
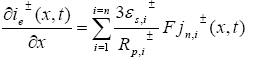 (20)
(20)
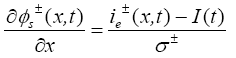 (21)
(21)
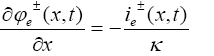 (22)
(22)
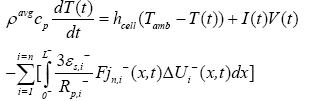 (23)
(23)
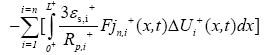
Boundary conditions for the above reduced order model are given by:
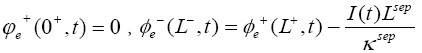
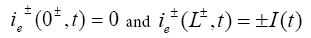
The initial conditions of this model are:
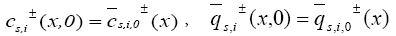 and
and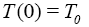
The output equation for this reduced order model remains the same as previously mentioned, i.e.
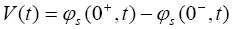 (24)
(24)
In PDAE observer equations, a feedback of error between the measured outputs and the calculated outputs [1] was introduced. This feedback was maintained in such a way that all the variables being estimated converges to their true values [17]. The PDAE observer gain are linear corrective terms via output injection only for the volume averaged concentrations in the individual electrodes and the internal average temperature [1]. The gain values were determined by trial and error method during the simulation for which the error value is the minimum one.
The PDAE observer equations are the followings:
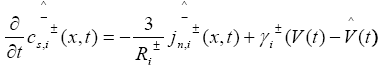 (25)
(25)
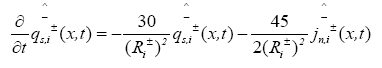 (26)
(26)
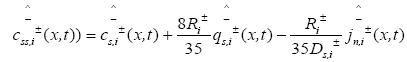 (27)
(27)
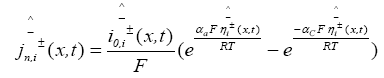 (28)
(28)
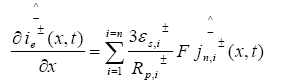 (29)
(29)
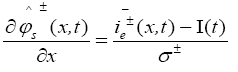 (30)
(30)
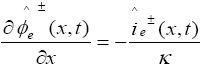 (31)
(31)
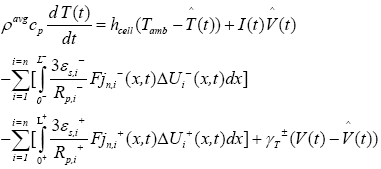 (32)
(32)
The output equation of the observer is:
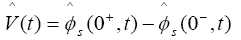 (33)
(33)
The equation of the observer gain in the two electrodes are given by
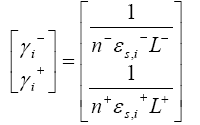
Where n, denotes number of active materials which is assumed one in this works. One important point to be noted in case of PDAE observer is that, the temperature was assumed to be constant at room temperature, i.e. 298.15K. Therefore, even though the temperature equation is provided in battery modeling part, the observer gain for temperature is not considered for this work, i.e. 
This adaptive estimation technique which is a special type of fault detection method is adopted in this work with the electrochemical model of Li-ion battery. In this estimation (MMAE) technique [7, 21- 25], as shown in Figure 2, various models run simultaneously while all the models are excited by a same input signal. MMAE in our work uses PDAE observer outputs of different models (coming from due to parameter variations). If there are total “n” models, there will be (n-1) outputs represents the faults or unhealthy scenarios [7], the remaining one is the actual plant model.
The distinguishing feature of MMAE technique is that, it provides a scope of fault detection based on possible fault scenarios along with the actual model. Main advantage of using MMAE as compared with other possible ways of fault detection (fuzzy logic, SVM etc.) is that, it provides a probabilistic approach of condition monitoring [7] based on the differences of outputs between the actual model and all other individual fault models which is more reliable in case of fault detection.
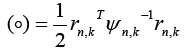
Here,
The conditional probabilities require a priori samples to compute the current values and are normalized over a complete sum of conditional probabilities of all systems. The probability for the nth model at time sample is given by [7,23,25,26]:
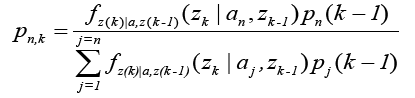
Where, 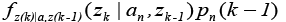 is the conditional probability density function of the nth model considering the history of the measurements.
is the conditional probability density function of the nth model considering the history of the measurements.
The conditional probability function is expressed as [23,25,26]:
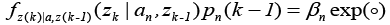
Where, 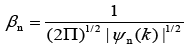
Where, l is the measurement dimension and equal to 1 and then:
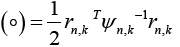
Where, 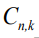 is the residual signal for the
is the residual signal for the  model at time sample k . When the output of any of the available models matches with the output of the actual model which simultaneously make the mean value of that residual signal to zero and the covariance of that particular signal is given by [23,25,26]:
model at time sample k . When the output of any of the available models matches with the output of the actual model which simultaneously make the mean value of that residual signal to zero and the covariance of that particular signal is given by [23,25,26]:
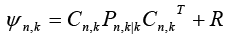
Where 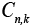 is the output vector for
is the output vector for 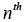 system at any time sample k . Moreover,
system at any time sample k . Moreover,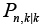 represents the state covariance matrix while R is covariance matrix of measurement noise.
represents the state covariance matrix while R is covariance matrix of measurement noise.
System Identification Toolbox in MATLAB was used to have matrices for all the scenarios. Using all possible residuals the conditional probabilities are evaluated. The largest conditional probability among all may be used as an indication of ongoing fault condition related to the involved specific residual [7].
Among all the electrochemical model parameters of the battery dynamics, there are some parameters which depend on the battery physics and on the other hand another type of parameters exist, which depend on the chemistry of the battery. Stated two types of parameters are adopted in this fault diagnosis work. In addition to these two type of parameters, there are some parameters, which were adopted from the manufacturer provided values.
Faults of the battery arises mainly due to the variation in some of the parameters in the battery electrochemical model. These variation differs from one possible model of the battery to others.
The parameters which are common to all possible scenarios of the battery, i.e. general parameters are provide in Table 1 [27]. Apart from these general parameters, the model specific parameters, which yields different possible battery operating scenarios are provided in Table 2 [27]. For the fault diagnosis purpose, the input current to the battery possible models is the scaled battery output current from a HEV simulation using a plug-n-play vehicle simulator, Autonomie [28], developed by Argonne National Laboratory.
| Symbol | Unit | Cathode | Separator | Anode |
|---|---|---|---|---|
| σi | S/m | 100 | 100 | |
| €f, i | 0.025 | 0.0326 | ||
| €i | 0.385 | 0.724 | 0.485 | |
| Cs, i, max | mol/m3 | 51554 | 30555 | |
| Cs,i,0 | mol/m3 | 0.4955×51554 | 0.8551×30555 | |
| C0 | mol/m3 | 1000 | ||
| C0 | m | 2×10-6 | 2×10-6 | |
| Li | m | 80×10-6 | 25×10-6 | 88×10-6 |
| RSEI | Ωm2 | 0 | 0 | 0 |
| F | C/mol | 96487 | 96487 | 96487 |
| R | J/(mol K) | 8.314 | 8.314 | 8.314 |
| T | K | 298.15 | 298.15 | 298.15 |
Table 1: Electrochemical model parameters for licoo2 cathode chemistry.
| Parameter | Healthy | Aged | OD | OC |
|---|---|---|---|---|
| D n (m2/s) | 3.9×10-14 | 4.875×10-15 | 7.8× 10-15 |
4.875×10-15 |
| D p(m2/s) | 1.0×10-14 | 1.5×10-14 | 5.0× 10-15 |
5.0× 10-15 |
| K n(mol/(sm2)/(mol/ m3) | 5.0307×10-11 | 6.288410-12 | 1.0061× 10-11 |
8.38× 10-12 |
| K n (mol/(sm2)/(mol/ m3) | 2.334× 10-11 |
2.334× 10-11 |
1.17× 10-11 |
1.17× 10-11 |
Table 2: Model Specific Parameters.
For this purpose, a portion of the UDDS cycle simulated battery output current profile is provided in Figure 3. Considering this current profile as input to the electrochemical model, all four of the battery models were simulated and the PDAE observer was used to observe the same output. In this work, voltage is the only state under consideration. In this work, the tuned value of observer gain is 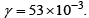
For healthy battery, the simulated and the observed voltage responses of the battery is provided in Figure 4. Similarly, the voltage comparison for the aged battery is provided in Figure 5. For Overdischarged battery, the voltage comparison is provided in Figure 6. In addition to those three models, for over-charged battery, the voltage comparison is provided in Figure 7. If the MMAE algorithm is observed carefully, it is clear that, the decision on the occurring faults are taken using the residual voltage signals. To have the residuals, a plant model voltage profile is taken as the reference, which is build following the following procedure shown in Figure 8.
Among 50 sec of battery operation, first 10 sec and last 5 sec is dominated by the healthy battery operation, after the first 10 sec of operation, next 15 sec is dominated by the aged battery chemistry, next 10 sec is dominated by OD battery operation and next 10 sec is from OC battery operation.
Using the above sequence of operations, the built plant model voltage profile is provided in Figure 8.
After comparing the PDAE observer voltage responses with this plant voltage profile, respective model voltage residuals are generated, which are used in fault diagnosis, i.e. used in conditional probability generation equation. Voltage residual for heathy battery operation during the overall operation of the battery is provided in Figure 9. Similarly, the voltage residual for the aged battery is provided in Figure 10. Voltage residual for the over-discharged battery is provided in Figure 11. Finally, the voltage residual for over-charged battery is provided in Figure 12.
To have the covariance of the particular signal updated state covariance matrix, is the significant one along with the measurement noise covariance matrix, . Using the system identification toolbox in MATLAB was used to generate the discrete time state space model using the UDDS current signal as input and respective model voltage as output and taking 0.001s as sample time. Having the discrete time state-space model, using the Kalman-gain generation loop, the updated state covariance matrices are generated for all four models.
Initialized values of the state covariance matrices are taken as the identity matrix of order two, i.e.
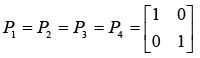
After evaluating the Kalman-gain generation loop, the updated state covariance matrices are provided below:
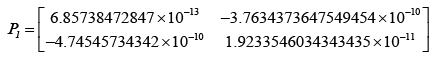
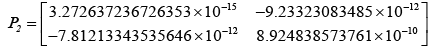
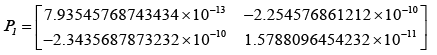
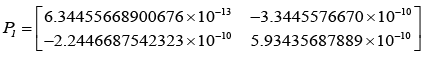
Adopting the updated state covariance matrices, probabilities were obtained for different values of measurement covariance matrices, R.
If the voltage residuals are observed, it is clear that, the maximum value of the residual is of the order of 10-3. Therefore, the values of R cannot exceed the maximum value of the residual. Hence, for different values of R, lower than the maximum residual values, the probabilities are obtained.
For R =1×10−5 the obtained probabilities for the fault diagnosis is provided in Figure 13.
This fault diagnosis is not the exact one to be used in the BMS. Therefore, value of was changed to and the obtained probabilities for this is provided in Figure 14.
Fault diagnosis of Li-Ion battery was implemented for a real time operation mode for HEV. An effective fault diagnosis technique, multiple model adaptive estimation (MMAE) was implemented for some crucial operation mode of Li-Ion battery. Some possible abusive operating conditions, i.e. over-discharged, over-charged and aged mode of operation was adopted along with the healthy operation of Li-Ion battery. The obtained probability of faults was correct enough to use in real time BMS of a HEV. Obtained results of fault diagnosis is based on the electrochemical model of the battery dynamics, therefore, the obtained fault diagnosis is more reliable and it can be thought for a potential real time application for HEV battery, where the BMS would be a reliable one because of the adopted fault diagnosis technique.