Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2022)
Earth’s well-known energy budget scheme is subjected to variations representing changes of insolation and atmospheric absorption. The Charney Report variability cases of doubled atmospheric CO2 concentration and insolation increase by 2% are found reproducible. The planetary emissivity is revealed linear to surface temperature, conformant with measurements. Atmospheric water vapor with its characteristic concentration-temperature dependency appears as a major component in earth’s energy balancing mechanisms. As part of this, rising temperatures bear the probability increase for rainfall shifts towards fewer and stronger events.
Climate forcing; Climate sensitivity; Earth energy budget; Planetary emissivity; Rainfall temperature dependency
A major aim of the present studies is the search for reproducibility on the results from sophisticated scientific research. Inherently, nature and climate are complex systems. Their understanding requires consideration of numerous aspects, each bound to coherently reflect the same system.
Earth’s energy budget sorts the underlying processes by a rather transparent set of rules. The master rule is given by the observation that at any condition through history, earth has managed to establish an energy-equilibrated state, thus avoiding runaway paths. Climate equilibrium states are characterized by balanced energy budgets, the entering energy flux equaling the emerging flux. This applies to the planetary earth-space system (shortwave insolation entering, longwave radiation emerging to space) as well as to the subsystems of atmosphere and surface.
The energy budget appears like an accounting scheme.
• The energy flux received on earth (mainly) originates from the shortwave insolation at the Top of the Atmosphere (TOA), reduced by the reflections from the planetary albedo. The emitted (longwave) energy flux is composed of the radiation from clouds, the (cloud-free) atmosphere, and the surface in the atmospheric window.
• The atmosphere receives energy from insolation (shortwave) absorption and from the surface via longwave absorption, evapotranspiration, and sensible heat; it emits radiation to the surface and into space from clouds and at clear sky.
• The surface absorbs a fraction of the (TOA) insolation and receives radiation from the atmosphere; it loses energy by radiation into space (in the atmospheric window) and into the atmosphere as well as by evapotranspiration and sensible heat. In addition, the surface (in this definition) exchanges energy with the oceans; in an equilibrium state, the exchange is balanced, i.e., the ocean heat uptake is zero. Earth surface emissivity is less than 1. For simplicity when translating between radiation and temperature, ideal black-body with emissivity equal 1 is assumed throughout the present study.
Earth’s energy budget-variability studies
The first three columns of Table 1 summarize the current energy budget [1]. Based on this reference data set, three variations are explored. In this procedure, three parameters are treated as fit variables: The longwave radiation from the atmosphere to the surface, the evapotranspiration and sensible heat component, and the longwave emittance to space from the clouds.
| Energy budget item | Notation | Reference data set | Variability case | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| I+2% | A+3°C | EC | |||
| SW (insolation) TOA | SWTOA, I | 341 | 347.8 | 341 | 341 |
| Planetary albedo | αR=(79+23)/SWTOA | 0,299 | |||
| SW absorption system | SWAbs=SWTOA∙(1-αR) | 239 | 244 | 239 | 239 |
| SW absorption atmosphere | SWAbsA=SWAbsA,R∙SWTOA/SWTOA,R | 78 | 80 | 78 | 78 |
| SW absorption surface | SWAbsS=SWAbs-SWAbsA | 161 | 164 | 161 | 161 |
| LW radiation atmosphere to surface | LWAS (free variable) | 333 | 347.5 | 350 | 346.5 |
| Evapotranspiration and sensible heat | ES (free variable) | 97 | 98 | 97 | 97 |
| Surface in | SRFin=SWAbsS+LWAS | 494 | 512 | 511 | 508 |
| Temperature surface (K) | TS=((SRFin-ES)/σ)1/4 | 289.3 | 292.3 | 292.3 | 291.7 |
| Atmospheric window fraction | Fwindow,R=LWwindow/(SRFin-ES)=40/396 | 10.10% | |||
| LW radiation atm. wind. | LWwindow= Fwindow,R∙(SRFin-ES) | 40 | 42 | 42 | 41 |
| LW radiation from surface to atmosphere | LWSA=SRFin-ES-LWwindow | 357 | 372 | 372 | 372 |
| Surface out | SRFout=ES+LWSA+LWwindow | 494 | 512 | 511 | 511 |
| Surface equilibrium | SRFout-SRFin=0! | ✔ | ✔ | ✔ | 3,2 |
| Atmosphere in | ATMin=SWAbsA+LWSA+ES | 532 | 549 | 547 | 547 |
| Clouds radiation fraction | Fcloud (free variable, 5.65% in [1]) | 5.60% | 5.80% | 5.20% | 5.80% |
| LW radiation clouds | LWcloud=Fcloud∙ATMin | 30 | 32 | 28 | 32 |
| LW radiation | LWatm | 169 | 170 | 169 | 169 |
| Atmosphere out | ATMout=LWAS+LWcloud+LWatm | 532 | 549 | 547 | 547 |
| Atmosphere equilibrium | ATMout-ATMin=0! | ✔ | ✔ | ✔ | ✔ |
| LW emissions to space | LWspace=LWwindow+LWcloud+LWatm | 239 | 244 | 239 | 242 |
| System equilibrium | LWspace-SWAbs=0! | ✔ | ✔ | ✔ | 3,2 |
| Planetary emissivity (pl. em.) | εp=LWspace/(SRFin-ES) | 0.602 | 0.589 | 0.578 | 0.59 |
| Temperature pl. em. (K) | Tp=(LWspace/σ)1/4 | 254.8 | 256.1 | 254.8 | 255.7 |
Note: Column 1: Budget item; SW: Shortwave; LW: Longwave. Column 2: Item abbreviation and relationship; subscript R: Value related to 3rd column; σ: Stefan-Boltzmann constant; surface emissivity =1. Column 3: data from [1], next columns with variations relative to column 3. Column 4: Variability case 1, insolation (TOA) +2%. Column 5: Variability case 2, longwave absorption in the atmosphere such that surface temperature +3°C. Column 6: Variability case 3, extra radiation from the surface with 3.2 W/m2.
Table 1: Earth energy budget: units W/m2, if not explicitly noted; bottom row: Black body temperature related to planetary emittance.
In variability case 1, the insolation at the top of the atmosphere is raised by 2%. In case 2, the longwave atmospheric absorption is increased such that the surface temperature is raised by 3°C. In case 3, an additional longwave radiation of 3.2 W/m2 is assumed to enter the atmosphere from below. The first two cases relate to variabilities studied earlier e.g., [2] with further references:The first case addressing an insolation increase, the second case an increase in atmospheric CO2 concentration. The third case relates to the anthropogenic energy consumption. The energy budget values of the three variability cases are computed from the reference data set as described in column 2 of Table 1.
The solutions for the free parameter values (Table 1) are nonunique. At first, their choice follows rather intuitive perception. At second, they may be adapted for consistency reasons, particularly related to the separately elaborated absorber density dependency [3] with water vapor as the dominant player. In this density dependency scheme, the absorber particle densities are related to the longwave absorption in the atmosphere and in turn, to the surface temperature. Results from the density scheme will subsequently be addressed, though without detailed description for conciseness reasons.
Discussion on the variability cases: Variability case 1, insolation increase by 2%. The surface temperature increase as given by the energy budget values is 3°C, the same as in [2] when applying a Sensitivity (S) of 0.75°C/(W/m2). Here, the sensitivity is defined as the ratio of surface temperature change (ΔTS) to TOA (longwave) emittance change (ΔLWspace), the latter equal to the change in planetary shortwave absorption (ΔSWAbs) between equilibrium states, hence S=ΔTS/ΔLWspace=ΔTS/ ΔSWAbs. The energy budget values of case 1 in Table 1 reveal a sensitivity of S=0.63°C/(W/m2) (case 1 versus reference data set, non-rounded). The emissivity is decreased and the planetary emittance temperature slightly increased relative to the reference case. The energy budget values are conformant with the mentioned density scheme of [3]: There, a temperature increase of 2.7°C is obtained as compared to the present 3°C from the energy budget, with a longwave radiation absorption rise of 14.7 W/m2 comparing to the increase of atmosphere-tosurface longwave radiation (LWAS) by 14.5 W/m2 in the energy budget scheme of Table 1.
Variability case 2, atmospheric longwave absorption increase leading to a 3°C-surface temperature rise. For the two states (lower and higher surface temperatures) in equilibrium to first order, the system (i.e., planetary) emerging radiation (LWspace) must remain constant, since the temperature-effective incoming radiation (SWAbs) is constant, with LWspace=SWAbs. As of Table 1, the emissivity is further decreased, to be explained by the absorber concentrations: The lowest concentrations relate to the reference case, mostly water vapor is added in case 1 due to surface temperature increase, then CO2 is primarily added in case 2. The energy budget consideration of Table 1 reveals an atmosphere-to-surface radiation gain (LWAS) of 17 W/m2 (case 2 vs. reference) in comparison to an absorption increase of 16 W/m2 in the mentioned density scheme, there with a 2.9°C-rise corresponding to the present 3°C from the energy budget. In the density scheme, the 2.9°C-16 W/m2-rise is reached at a CO2 level of 440 ppmv as opposed to 570 ppmv in [2], or 4°C with 510 ppmv in comparison to 570 ppmv as more recently referred [4].
Variability case 3, additional longwave emissions from the surface by 3.2 W/m2. Division of the 2.4°C-temperature increase (column 6 vs. column 3 for temperature in Table 1) by the extra radiation of 3.2 W/m2 reveals a sensitivity of 0.75°C/(W/m2). The equilibrium condition of Table 1 needs to be fulfilled for the atmosphere (see ‘✔’-sign). For the surface and the planetary system, the outgoing radiation must equal the incoming ones plus the additional radiation of 3.2 W/m2 to retain energy balance. The density scheme [3] delivers 2.35°C as compared to the 2.4°C from the energy budget consideration.
Further variability cases. Additional energy budget estimates have been performed on the zonal (polar vs. tropical) conditions, on the glacial-interglacial conditions [5], on atmospheric absorption increases effecting the surface temperature to rise by 10 and 20°C (as further variations of case 2), changing of the insolation by -4% and +5.5% (as further variations of case 1), changing of the insolation by +4% and simultaneously of the absorption with an additional 6°C-effect (coupling cases 1 and 2), and representing the faint young Sun conditions (low insolation, high surface temperature, high pCO2, low pO2, partly low continental coverage). The energy budget estimates are again well reflected by the absorbing particle densities in the density scheme (i.e. to first order of H2O and CO2, the former significantly dominating).
For all variability cases, variations to the algorithms of Table 1-specifically, altering albedo and atmospheric shortwave absorption in dependence on surface temperature-leave the described results unchanged (details not shown).
Conclusion: The Charney Report variabilities, i.e., insolation and CO2 concentration change, can be reproduced within the energy budget. Equilibrium requires TOA longwave emittance to change with absorbed shortwave irradiation in case of insolation change, and TOA longwave emittance to remain constant in case of absorber change (e.g., of CO2 concentration). Already inferring from case 1, emissivity is decreasing with insolation increase and entailed surface temperature increase. This indicates that water vapor is predominantly regulating emissivity in response to temperature-with two characteristics acting in concert, water vapor as the major longwave absorber and its concentration relatively strongly dependent on temperature.
Planetary emissivity from the variability studies
In view of all variability cases, the planetary emissivity (εp) appears to linearly correlate with the surface temperature (Ts) as summarized in Figure 1, the relationship for the energy-balanced cases represented by Ts=(-161∙ εp+386) K within ± 2% deviation from the energy budget values. The zonal conditions (orange diamonds, dotted line) exhibit energy flux imbalances, while balance is given in all other cases. The linear relationship appears independent of the driving force (atmospheric longwave absorption and insolation examined here) and applies to a wide range of climate conditions (between-10 and +20°C from today’s temperature). The relationship is comprehended as an intrinsic property of the energy balancing mechanisms, largely originating from the atmospheric water vapor which is temperature-dependent in amount, itself significantly determining the surface temperature, and leaving the emittance to space rather slowly varying. Also, clear-sky measurements reveal a linear relationship between Outgoing Longwave Radiation (OLR) and near-surface temperature [6]. This is consistent with the present linear emissivity-temperature relationship if clouds contribute positively to OLR at cold and negatively at warm surface temperatures, of the order +25 and -55 W/m2 at 200 and 300 K, respectively. This translates to a cloud feedback parameter of 0.8 W/m2/K.
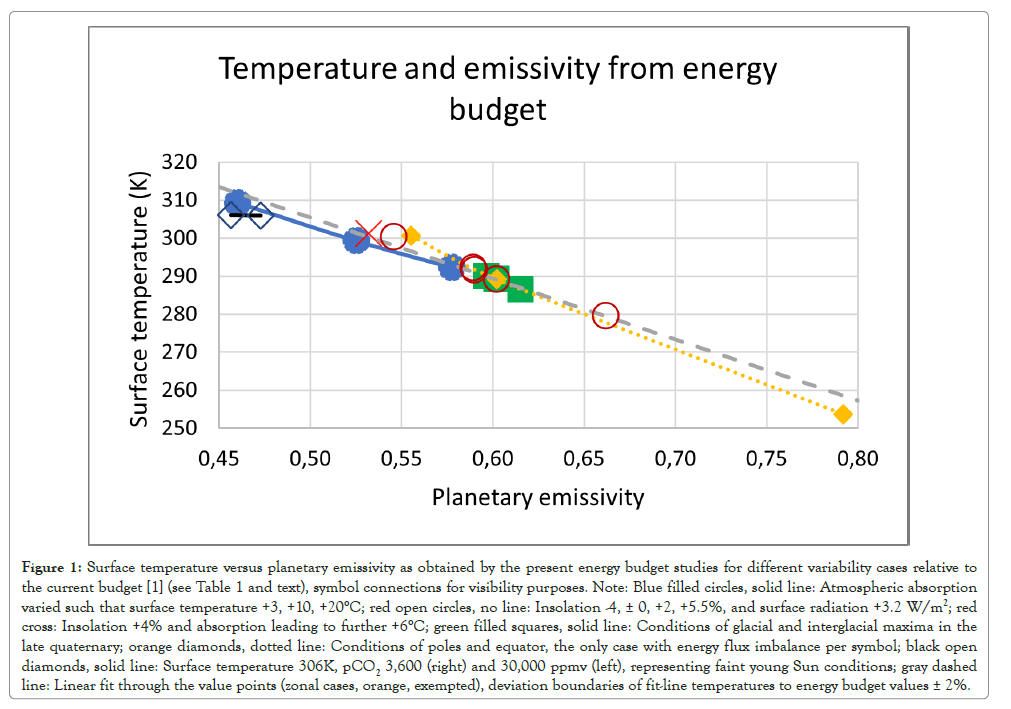
Figure 1: Surface temperature versus planetary emissivity as obtained by the present energy budget studies for different variability cases relative to the current budget [1] (see Table 1 and text), symbol connections for visibility purposes. Note: Blue filled circles, solid line: Atmospheric absorption varied such that surface temperature +3, +10, +20°C; red open circles, no line: Insolation -4, ± 0, +2, +5.5%, and surface radiation +3.2 W/m2; red cross: Insolation +4% and absorption leading to further +6°C; green filled squares, solid line: Conditions of glacial and interglacial maxima in the late quaternary; orange diamonds, dotted line: Conditions of poles and equator, the only case with energy flux imbalance per symbol; black open diamonds, solid line: Surface temperature 306K, pCO2 3,600 (right) and 30,000 ppmv (left), representing faint young Sun conditions; gray dashed line: Linear fit through the value points (zonal cases, orange, exempted), deviation boundaries of fit-line temperatures to energy budget values ± 2%.
For equilibrium states, the predominant role of water vapor demands its atmospheric residence time to roughly scale with the concentration dependence on the surface temperature. This is necessary to bring the relatively high concentration variability (exponential dependency on temperature according to the Clausius-Clapeyron relation) in line with the relatively stable evapotranspiration and precipitation energy contributions (amounting to ca. 83% of ES in Table 1; changing by the order of 0.5%/°C in the energy budget estimates, details not shown). As a result, mean precipitation remains rather constant. On the other hand, a simultaneous increase of water vapor concentration and residence time lays the foundation for frequency decrease of high-intensity rainfall with rising intensity per event.
It appears interesting that the simple energy budget consideration reveals important intrinsic characteristics of nature: Emissivity to inverse-linearly follow surface temperature, this independent of the temperature-driving agent; water vapor as a dominant component in earth’s energy balancing mechanisms, controlled by the characteristic temperature dependency of its concentration; the strongly varying water vapor concentration in combination with the weakly varying evapotranspiration laying the foundation for rainfall pattern changes with temperature. The prominent role of water vapor, with CO2 in conjunction, is confirmed by a density-based description [3].
The energy budget study is viewed complementary to the radiative forcing-concept. For completed transitions between equilibrium states, it avoids situations where the feedback parameter (in its typical definition) is predetermined to zero (in case of longwave absorber change: TOA radiation constant while surface temperature changing), which is equivalent to infinite sensitivity and undefined temperature change in the frequently presented formalism [7]. Within the transitions between equilibrium states (transient climates), potential (TOA) radiation imbalance is generally comprehended to be dominated by ocean heat uptake [8].
The forcing concept’s starting point of TOA longwave radiation changing with surface temperature by T3 (Planck feedback) is put into perspective. For equilibrium states, the energy budget reveals an intrinsic linear behaviour, i.e., planetary emissivity changing via a constant instead of T3, in line with observations. This is fundamentally attributed to atmospheric water vapor with its absorption and concentration-temperature properties. For the transient regime, a first look is to be directed at the atmosphere-ocean interplay.
The energy budget scheme may serve as a shortcut to cumbersome regression analysis of sophisticated simulation results. A handy tool is provided for quick insight in equilibrium cases.
All data and code are available: https://www.dropbox.com/scl/fi/ypxndn86aikv225u4kldj/Energy-budgets-in-balanced-climates-Data-and-code.xlsx?dl=0&rlkey=13fgx24wf91qfy88y486jlsdq
No conflict of interest is to be declared.
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
Citation: Anderl T (2022) Earth's Balanced Climates in View of their Energy Budgets. J Phys Chem Biophys. S1:001.
Received: 11-Feb-2022, Manuscript No. JPCB-22-16070; Editor assigned: 14-Feb-2022, Pre QC No. JPCB-22-16070 (PQ); Reviewed: 28-Feb-2022, QC No. JPCB-22-16070; Revised: 07-Mar-2022, Manuscript No. JPCB-22-16070 (R); Published: 14-Mar-2022 , DOI: 10.35248/2161-0398-22.S1.001
Copyright: © 2022 Anderl T. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.