Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2016) Volume 5, Issue 2
Rocket motors are widely used to generate thrust or impulsive force to impart a desired velocity to flight vehicle to transport its payload to the intended destination. The working principle of Rocket motor is mainly Newton’s 2nd and 3rd laws. Rocket motors are non-air breathing propulsion class i.e., won’t require oxygen from the atmosphere for combustion of the fuel which is stored in the rocket motor. During the operating conditions of the motor hardware, it will be subjected to high temperatures and pressure loads. Structural and thermal design has to carried out for a given input parameters and analysis to be carried out to check the stress levels and temperatures on the hardware. The present paper deals with structural design of motor hardware. The main input parameters considered are the maximum operating pressure and maximum diameter of the Motor hardware. The material properties considered are up to 100°C. Structural analysis and fracture analysis are to carry out after the design of each component of the rocket motor hardware. For design, the motor hardware is considered as a pressure vessel. To compute parameters like thickness some initial assumptions were made. 2D drawing is developed using Auto Cad software and structural analysis is carried out in ANSYS. This software employs finite element analysis techniques to generate the solution. Hence the displacement magnitude, von mises stress and strain developed within the motor is pictorially visualized. Fracture analysis is also carried out on the material.
<Keywords: Ansys; Finite element analysis; Fracture analysis; Motor casing; Solid rocket motor; Stress; Strains; Structural analysis
Rocket motors are non-air breathing propulsion class i.e., won’t require oxygen from the atmosphere for combustion of the fuel which is stored in the rocket motor [1]. A rocket motor is a typical energy transfer system. The chemical energy inside the fuel is converted to the thermal energy by a combustion process. High pressure and high temperature combustion product gases are expanded through a converging-diverging nozzle. By this process “internal energy of the gas is converted into kinetic energy of the exhaust flow and the thrust is produced by the gas pressure on the surfaces exposed to the gas” [2].
Solid propellant rocket motor is the most commonly used compared to other rocket motors due to its relatively simple design, high reliability, ease of manufacture and ready to use on demand etc. Since solid-fuel rockets can remain in storage for long periods, and then reliably launch on short notice, they have been frequently used in military applications such as missiles. Solids are, however, frequently used as strap-on boosters to increase payload capacity or as spin-stabilized add-on upper stages when higher-than-normal velocities are required. Solid Rocket Motor can be used for a wide variety of applications requiring wide range of magnitude of thrust [3].
The design and the construction of the solid rocket motor hardware involve consideration of various stresses acting on the motor hardware due to pressure and thermal loads. For this analysis to be done, selection of material and their properties, motor hardware performance and operating conditions, a few design considerations, etc.., are the parameters required to be studied to obtain the solution.
Solid rockets were invented by the Chinese; the earliest versions were recorded in the 13th century. Hyder Ali, king of Mysore, developed war rockets with an important change: the use of metal cylinders to contain the combustion powder [4]. Rocket propulsion system is a non-air breathing system, in which the propulsive effort or thrust is obtained by variation of the momentum of the system itself. They do not depend on the atmospheric air, either as oxidizer. As its name implies, the propellant of the motor is in the solid state. The oxidizer and the fuel is premixed and is contained and stored directly in the combustion chamber [5]. Since the solid propellant both includes fuel and oxidizer, solid propellant rocket motors can operate in all environmental conditions. In comparison to other types of rockets, solid propellant rocket motors have simple design, are easy to apply and require little or no maintenance. Rocket motor propulsion can be classified based on the type of propellant of rocket propulsion units used in a given vehicle and type of construction, the number by the method of producing thrust. Even though there are many rocket propulsion types only chemical rocket propulsion is widely used [6]. Other rocket propulsions have their drawbacks in the weight consideration and thrust produced. Further advancements in technologies may lead to usage of other rocket propulsion systems in future.
A simple solid rocket motor consists of a Motor casing, Nozzle, propellant grain and igniter (Figure 1).
Motor case
The combustion takes place in the motor case; therefore, sometimes it is referred to as combustion chamber. The case must be capable of withstanding the internal pressure resulting from the motor operation, approximately 3-30 MPa, with a sufficient safety factor. Therefore motor case is usually made either from metal (high-resistance steels or high strength aluminum alloys) or from composite materials (Glass, Kevlar and Carbon).
Insulation
High temperature of the combustion gases, ranging from approximately 2000 to3500 K, requires the protection of the motor case or other structural subcomponents of the rocket motor. Typical insulator materials have low thermal conductivity, high heat capacity and usually they are capable of ablative cooling. Most commonly used insulation materials are EPDM (Ethylene Propylene Diene Monomer) with addition of reinforcing materials.
Igniter
The ignition system gives the energy to the propellant surface necessary to initiate combustion. Ignition usually starts with an electrical signal. The ignition charge have a high specific energy, they are designed to release either gases or solid particles. Conventional heat releasing compounds are usually pyrotechnic materials, black powder, metal-oxidant formulations and conventional solid rocket propellant.
Nozzle
High temperature, high pressure combustion gases are discharged through the converging-diverging nozzle. By this way, chemical energy of the propellant is converted to kinetic energy and thrust is obtained. The geometry of the nozzle directly determines how much of the total energy is converted to kinetic energy. Therefore nozzle design has a very important role on the performance of a rocket motor.
The grain behaves like a solid mass, burning in a predictable fashion and producing exhaust gases. The nozzle dimensions are calculated to maintain a design chamber pressure, while producing thrust from the exhaust gases. Once ignited, a simple solid rocket motor cannot be shut off, because it contains all the ingredients necessary for combustion within the chamber in which they are burned. More advanced solid rocket motors can not only be throttled but also be extinguished and then re-ignited by controlling the nozzle geometry or through the use of vent ports.
Design inputs
Maximum Expected Operating Pressure (MEOP) considered is 150 ksc which normally can be obtained from the ballistic design. The motor maximum diameter considered is 200 mm. Motor hardware design is carried out using pressure vessel code.
Solid rocket motor or pressure vessel consists of the following components
i) Cylindrical Motor casing
ii) Head end and nozzle end domes
iii) Head end and nozzle end flange
iv) Convergent divergent nozzle
v) Head end cover
vi) Bolted Joint between motor- nozzle and motor –head end cover
Material selection criteria
Maraging steel -250 grades (MDN-250) is chosen to minimize the hardware weight due to its high specific strength. Moreover, it is easily available and fabrication technology is well established. This material has been widely being used in space and defense programs.
The detailed data on the chemical composition and mechanical properties are as given below.
Chemical Composition (Wt. %):
C: 0.03 Max.
Mn: 0.1 Max.
Si: 0.1 Max.
Ni: 17 - 19
Mo: 4.6 - 5.2
Co: 7 - 8.5
Ti: 0.3 - 0.5
Mechanical Properties of maraging steel:
UTS (MPa) : 1750 MPa
Y.S. (MPa) : 1680 MPa
Elongation(%) : 15
KIC fracture toughness: 80 MPa-m½
Young's modulus : 210 GPa
Factor of safety selection criteria: As per AVP –32 and MIL standards, the following safety factors have been chosen.
On Ultimate tensile Strength (UTS) : 1.5
On Yield Strength : 1.33
Allowable Ultimate tensile stress: 175/1.5 = 116.6 kgf/mm2
Allowable Yield stress : 126 kgf/mm2
Lowest of above two allowable stresses is on UTS (116.6 N/mm2) is taken for design.
Design inputs
In brief, the following inputs have been taken for motors hardware design.
i) Material = Maraging steel (250 grade)
ii) Motor outer diameter (D) = 200 mm
iii) MEOP (P) = 150 kgf/cm2
iv) UTS = 175kgf/mm2
v) Yield strength = 168kgf/mm2
vi) Factor of safety (F.S.) = 1.5 on UTS
vii) Weld efficiency (E) = 90%
viii) Biaxial gain = 1.1(10%)
vii) Mismatch factor = 1.15 (5%)
Thickness of motor casing:
The cylindrical shell thickness is calculated by using conventional formula from ASME Pressure vessel code. It is given by
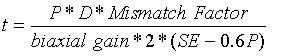
The Cylindrical shell is assumed to be made from the sheet which is rolled and weld method. In this case, both mismatch factor and weld efficiency (E) have to consider.
Allowable strength(S) : UTS/F.S.
Calculated thickness (t) : 1.506 mm
Head end and nozzle end dome:
Various domes shapes viz. ellipsoidal, hemispherical, tori spherical etc are used in pressure vessel. The shape of the dome considered is Tori-spherical type because of easy fabrication compared to other shapes. This is assumed to fabricate from the forged rod of 200 mm diameter. After iterations, the following parameters are chosen to get optimum parameters
Crown Radius (L) = 150 mm
Knuckle radius (r) = 15% of ‘L’ = 22.5 mm
L/r = 6.6 mm
M = 0.25*(3+ √(L/r)
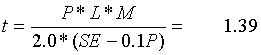
Thickness (t) = 1.347 mm
Head end flange design and bolted joint between motor–head end cover
Schneider’s approach is used to calculate the flange thickness and to finalize the size and number of bolts 12.9 grade Socket head bolts are considered for design.
Head end opening diameter: 333 mm
MEOP : 1.5 kg/mm2
Factor of safety considered: 1.5
No. of studs assumed : 24 No. s
Bolt size and class : M6 x 1.0, 12.9 class
N = No. of bolts/mm of stud circle circumference = 24/468.1 = 0.0512
Circumferential pitch (d) = π x 149/(24 x 10) = 2.43
A = Minimum required area/bolt
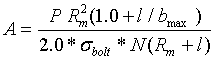 = 35.9 mm2
= 35.9 mm2
Where
σbolt = yield strength of the bolt = 108 kg/mm2
M6 x 1.0 bolt having cross sectional area 36.6 mm2
Thickness of flange can be calculated by
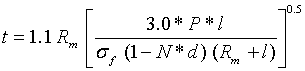
t = 7.22 mm
Thickness chosen: 8.0 mm;
Max. stress on each bolt due to pressure load and preload
Stress due to pre load on each bolt = 0.4 σyield_bolt = 36.0 kg/mm2
Stress due to pressure load on each bolt = 11.3 kg/mm2
Total stress on each bolt = 36.0+11.3 = 47.3 kg/mm2
Factor of safety available on each bolt: 1.90 on yield strength
Head end cover
Head end cover thickness can be same as flange but it is a flat plate, the thickness has to be calculated by using flat plate closure with bolted joint formula and higher one has to be finalized. Flat plate with bolted joint formula given in pressure vessel code is
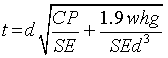
Where d = Diameter up to the centre of ‘O’ ring = 156 mm
C = 0.3
P = 1.5 kgf/ mm2
E = 1
W = π/4 d2p = 35668 kgf
hg = 10.5 mm
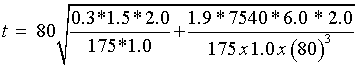 t = 11.09 mm
t = 11.09 mm
Nozzle end flange design and bolted joint between motor – nozzle
Schneider’s approach is used to calculate the flange thickness and to finalize the size and number of bolts 12.9 grade Socket head bolts are considered for design.
Head end opening diameter: 667 mm
MEOP: 1.5 kg/mm2
Factor of safety considered: 1.5
No. of studs assumed: 24 No. s
Bolt size and class: M6 x 1.0, 12.9 class
N = No. of bolts/mm of stud circle circumference
= 24/468.1 = 0.0512
Circumferential pitch (d) = π x 149/(24 x 10) = 2.43
A = Minimum required area/bolt
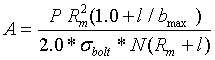 = 35.9 mm2
= 35.9 mm2
Where
σbolt = yield strength of the bolt = 108 kg/mm2
M6 x 1.0 bolt having cross sectional area 36.6 mm2
Thickness of flange can be calculated by
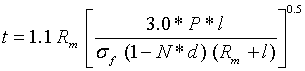
t = 7.22 mm
Thickness chosen: 8.0 mm;
Max. Stress on each bolt due to pressure load and preload
Stress due to pre load on each bolt=0.4yield_bolt = 36.0 kg/mm2
Stress due to pressure load on each bolt = 11.3 kg/mm2
Total stress on each bolt = 36.0+11.3 = 47.3 kg/mm2
Factor of safety available on each bolt: 1.90 on yield strength
Nozzle design
Nozzle is a convergent – divergent conical nozzle. It is designed with an area ratio of 9. This is planned to fabricate from the forged rod of 200mm diameter.
Nozzle throat diameter: 35 mm
Nozzle exit diameter: 105 mm
Convergent diameter: 200 mm
Area of the divergent ratio: 9
Nozzle Convergent Thickness: Convergent thickness is designed by using conical shell formula
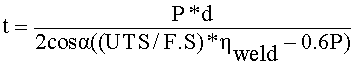
α = half of the included angle of the cone = 55°
By formula thickness (t): 1.511 mm
Nozzle throat metal backup thickness: The pressure at nozzle throat section will be approximately 0.54Pc. Therefore, at the throat metal back up
Pt = 0.54Pc
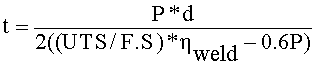
Where
Throat back up diameter : 35 mm
Pressure at throat : 81 ksc
Thickness by formula : 0.32 mm
Thickness chosen : 1.0 mm (from fabrication point of view)
Nozzle divergent thickness: Nozzle divergent thickness is with conical shell formula
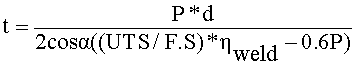
α = half of the included angle of the cone = 14°
Thickness obtained is 0.7 mm. The thickness obtained is very small; however from the manufacturing point of view a minimum thickness of 1.0 mm is selected (Figures 2 and 3).
Structural analysis of solid rocket motor hardware
The operating maximum internal pressure of motor is 150 ksc. Finite Element analysis of above motor is done for internal pressure.
Material properties:
Following material properties are considered in this analysis
Material: Maraging steel (MDN-250)
UTS: 175 Kgf/mm2
YS: 168 Kgf/mm2
E: 19000 Kg/mm2
ν : 0.3
Weld zone properties:
Weld efficiency: 90%
UTS: 120 Kg/mm2
YS: 108 Kg/mm2
Allowable stress:
Factor of safety on UTS is 1.5 and factor of safety on YS is 1.33
σall = minimum of (σuts/1.5, σy.s/ı.3)
= min (116.6, 126.3)
In Parent material = 116.6 Kg/mm2
In weld zone = 80 Kg/mm2
Axisymmetric Finite Element model of motor casing is prepared by using 8-nodded axisymmetric element, (plane 183). Stress analysis of model is carried out for internal pressure of 150KSc by fixing upper bulkhead portion. FE model with boundary condition is shown in the Figures. Stresses at different location are given in Table 1 and locations are shown in Figures. Stress pattern is also shown in Figures 4-10.
| Location | Von misses | F.S. on UTS |
|---|---|---|
| Von misses | ||
| A | 44.77 | 1.95 |
| B | 94.23 | 0.93 |
| C | 132.77 | 0.66 |
| D | 80.32 | 1.1 |
| E | 77.73 | 1.13 |
| F | 77.73 | 1.13 |
| G | 164.87 | 0.53 |
| H | 121.3 | 0.72 |
| I | 78.12 | 1.12 |
Table 1: Stresses at different locations.
Flange joint is modeled by arresting relative nodal displacement in appropriate direction. This will not give accurate result for bolt stresses, but our aim is to find out the stresses in casing only and this model will fulfill our requirements.
The traditional design approach of rocket motor case is generally based on thin shell theory wherein the ultimate or yield strength of the material enters the design along with the chosen safety factors. However, it is well known that the strength-based design carries with it an inherent assumption that the material is free from flaws and perfect fabrication [7]. But in practice, the material may contain voids, cracks or some induced cracks in weldment and during weld repair process. These flaws can act on sites for crack initiation under certain conditions of operation and leads to catastrophic failure of the motor case.
Fracture analysis makes it possible to determine the critical crack size dimensions in selected motor case thickness for known fracture toughness of the material, which leads to failure. Based on analysis, the designer can specify the critical flaw sizes to take care in the raw material and inspection stage and selection of the material based on its fracture toughness value. For the present analysis, the following design inputs have been considered Figure 11.
Design inputs
Material: Maraging steel-250 grade
Yield strength of the material (σys ) : 168 kgf/mm2
Plane strain fracture toughness on parent metal (KIC ) : 90 MPa√m
Plane strain fracture toughness on weldment (KIC ) : 75 MPa√m
: 241.5 kg/mm3/2
Plane stress fracture toughness on parent metal (KC) : 120-140MPa√m
The thickness of the motor case hardware (t) : 1.5 mm.
MEOP (P): 150 ksc
Motor outer diameter (D): 200 mm
The state of stress exists in thin shells is plane stress condition, whereas in thick shells it is a plane strain condition. The minimum thickness to achieve the plane strain conditions is given by
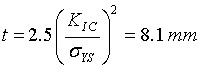
The present motor case thickness is 1.5 mm. So, the plane stress fracture toughness (Kc-max) is relevant rather than the plane-strain fracture toughness. However, the plain strain condition is considered for this analysis due to the following reasons.
i) The plain strain fracture toughness(KIC) is a material property like UTS, yield strength etc. and it is independent of thickness of material and flaw geometry for high strength materials. Whereas
ii) The plane stress fracture toughness (KC) is not independent of material property but it depends on thickness of material, flaw geometry and its dimensions.
iii) “KIC” of the given material will be lower than “KC”. Consideration of KIC for design is more conservative and the number of allowable crack sizes also can be reduced. The present motor case is having number of weld joints. The welded motor case fracture toughness will be lower than parent metal fracture toughness.
Hence, the plane strain fracture toughness of weld ment of 75 MPa √m (assumed) is taken for analysis. The next assumption is that the flaw present is in such an orientation that it would tend to open up under the tangential stress. Elliptical surface flaws have been considered, as they tend to propagate at a faster rate than the embedded flaws. The stress intensity factor is more in elliptical surface flaws.
The general relation among KIC , applied membrane stress(σ ) and flaw size (a) for elliptical surface flaws is given by
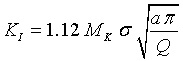
Where
KI= Stress intensity for a given flaw size and stress ratio (σ/σys )
Q = Flaw shape parameter which is a function flaw aspect ratio (a/2c) and stress ratio
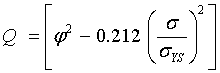
φ = elliptical integral of the second kind which is given by
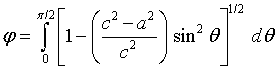

Mk = Back correction factor based on flaws depth to thickness ratio
Constant 1.12 = Front free surface correction factor, this value equal to 1.0 for embedded cracks.
σ = Operating stress (hoop stress in the present case)
a = Crack depth (half of minor axis of ellipse)
c = Semi-crack length (semi major axis of ellipse)
Any meaningful fracture analysis is possible when industry data on minimum detectable flaw size with a specified degree of reliability and confidence levels is available. The minimum detectable flaw size invariably has to be validated at shop floor level and is a function of many factors viz, material properties, thickness in question, NDT methods used vis-à-vis state of art, NDT inspector`s skill etc. For the sake of present analysis a set of flaw sizes have been assumed based on past industry experience on maraging steel plates and forgings.
Analysis:
Hoop stress due to internal pressure (σ) = PD/2t
= (1.5*178)/(2.0*1.5)
=100 kg/mm2
Stress ratio (σ/σYS) = 0.69
Comments:
Fracture analysis has been carried out for different flaw depths ranging from 0.5 mm to 1.2 mm and flaw length of 2 mm to 5 mm. It is seen from the results that up to crack depth of 1.2 mm and crack width of 2.5 mm for all the cases, the stress intensity levels are within limits and the factor of safety available is fairly good.
From the crack depth 1.5and crack width 3, the flaws detected are critical where stress intensity levels are high and FOS is not satisfied. However, these critical cracks can be detected through F_notch and G_notch NDT methods.
On observing all the results we got from ANSYS it is clear that the design can withstand the stresses produced because of the pressure of 150 Kg-f/cm2. Since the stresses developed are lower than the UTS of the material i.e., 175 Kg-f/mm2 = 1716.164 N/mm2 and the factor of safety FOS obtained higher than the design FOS value. The deformations of the casing are also known and plotted in the analysis portion. The maximum deformation occurred in the casing is at divergent portion of the nozzle and its value is 1.087 mm.
We have also found the various allowable crack lengths which can be withstand by casing and also the critical crack lengths which cannot be withstand by the material. By knowing these critical crack lengths we can estimate the allowable crack lengths in imperfections during the manufacturing process.
After structural analysis of the Rocket motor casing it is clear that the stress developed at various locations of the casing are within allowable limit and a factor of safety of (FOS) 1.5 is obtained by designing the casing using ASME codes.
The deformation of the casing is also known using ANSYS and the maximum deformation value is given by 1.08 mm. And the maximum deformation occurred is located at the end portion of the divergent section of the nozzle.
It is seen that all crack sizes (and aspect ratios) considered, the corresponding critical crack sizes are well above the NDT detectable methods. The thickness of 1.5 mm motor casing with less than critical crack sizes will not affect based on fracture.