In situations where protein X-ray structure or related structures for template-based homology modeling are unavailable for structure based virtual screening, computational methods for drug design rely principally on ligand-based approaches. Ligand-based approach depends on at least one known active compound; which serves as the query for searching library of compounds using predefined molecular descriptor parameters [1,2]. Three categories of chemical descriptors have been characterized till date; physical properties descriptors (1D-descriptor), molecular topology and pharmacophore descriptors (2D-descriptors) and geometrical descriptors (3D-descriptors, often requires prior knowledge of target protein binding-pocket) [3-5]. When there are multiple bioactive compounds for a given target, quantitative structure activity relationships (QSARs) method is more beneficial. QSAR method provides predictive mathematical model for biological activities using statistical clustering of multiple descriptors variables [6,7]. We sought to derive a mathematical equation from minimal set of ligand descriptors for set of Lysophosphatidic acid receptor (LPA1) inhibitors. With this equation, we hope to accurately predict the activity of a test set and hopefully used in ligand-based virtual screening for new high-affinity LPA1 antagonists.

Here, using Molecular Operating Environment (MOE) [8], multiple descriptors (SlogP (SlogP_VSA0-6), SMR (SMR_VSA0-4), a_acc, ASA, E_stb, a_hyd, and Kier (Kier1-2, KierA1-2)) [8] have been generated for training set of compounds (CHEMBL3819) in order to establish a mathematical equation to model LPA1 inhibition (antagonism). PCA analysis was also conducted to determine the principle components of the equation using scientific vector language (SVL) programming built into the MOE.

First, The IC-50 values of 134 unique entries (LPA1 inhibitors) from ChemBL database (CHEMBL3819) were converted to Gibb’s free energy of binding using Cheng-Prusoff equation [9] {Equation1} at S<<

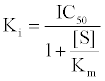                                                                                                                                                 (1)

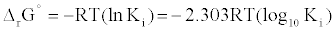                                                                     (2)

The library was randomly and unbiasedly grouped OCHEM server [10] into the training (120 compounds, Supplementary Figure 1) and test (14 compounds) sets. The training set was initially fitted using partial least square (PLS) method into all Chemical descriptors implemented in MOE [8]. The descriptors were pruned in order of their relative importance until a mathematical model (Equation 3) was obtained.

dGExpt = -3.0345 -0.39537 x a_acc -0.02183 x ASA -0.36027 x a_hyd -0.01028 x E_stb +0.64979 x Kier1 +0.21026 x Kier2 +0.08358 x KierA1 -0.47849 x KierA2 +0.03617 x SlogP_VSA0 +0.01945 x SlogP_ VSA1 +0.00494 x SlogP_VSA2 -0.00339 x SlogP_ VSA3 +0.01846 x SlogP_VSA4 +0.05076 x SlogP_VSA6 -0.06603 x SMR_VSA0 -0.05469 x SMR_VSA1 -0.03451 x SMR_VSA2 +0.00294 x SMR_VSA3 -0.01021 x SMR_VSA4 (Equation 3)

This model gives a high probabilistic (r²=0.79168 with RMSE of 0.61459 dGexpt) Gibb’s free energy prediction using minimal set of descriptors (Figure 1). A cross-validated correlation coefficient value of 0.70939 (RMSE = 0.72938) was also obtained for the model.

Figure 1: Scatter plot showing the predicted and experimental free energy of LPA1 inhibitors.

These results suggest that the set of descriptors chosen can effectively cluster the minimal structural and molecular parameters required for the predicting relatively small differences in the ligand activity of structurally diverse compounds typifying the training set.

Due to the relatively good mathematical correlation between the descriptors and the estimated free energy of ligand binding, we sought to further study the dataset descriptors long the principle components through the reduction of the dimensionality and linear transformation of the raw data (Principal component analysis (PCA)) [11]. Given the initial 120 compounds (represented as m) and for one of the compounds say ‘i’ its descriptors are represented by n-vector of real numbers xi=(xi1,..,xin, where n=1-17). Assuming that each molecule ‘i’ has an associated importance weight ‘wi’, (non-negative, real number) and that the weights is relative probability that the associated molecule ‘xi’ will be encountered (adding up to 1); If ‘W’ denotes the sum of all the weights then, the eigenvalues and eigenvectors for the final data are estimable from the raw data using equation (4) where S is a symmetric, semi-definite sample covariance matrix. S can be diagonalized such that S =Q^TDDQ (Q is orthogonal, D is diagonal-sorted in descending order from top left to bottom right) [12].

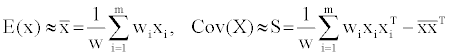                                         (4)

The effect of the each of the principal components (eigenvectors) on the condition and the variance (Supplementary Table 1) shows that nine (9) principal components sufficiently accounts for more than 98% of the variance in the dataset with a fitting mathematical equation (Equation 5). The 3D-scatter plot of the last three principal components (PCA7, PCA8 and PCA9) with respect to free energy is shown in Figure 2; each point in the plot corresponds to a molecule colored according to free energy values.

Figure 2: 3D PCA plot of each test compound. Colours represent experimental free energy.

PCA9 = 5.53218413e-001 -1.47174139e-003 X ASA -5.28867555e- 004 X E_stb - 9.64502253e-003 X Kier1 +2.92612997e-002 X Kier2 -9.05227786e-004 X KierA1+2.57936088e-002 X KierA2 +4.04361621e- 002 X SMR_VSA0-2.37125484e-002 X SMR_VSA1 +5.03998977e-002 X SMR_VSA2 +8.13078695e-003 X SlogP_VSA0 - 1.03630885e-002 X SlogP_VSA1 -5.72337043e-002 X SlogP_VSA2 -1.64177905e-003 X SlogP_VSA3 -7.55989243e-002 X SlogP_VSA4 -1.02026342e-002 X SlogP_VSA6 +1.79553609e-001 X a_acc -3.68295238e-002 X a_hydPCA9 = 5.53218413e-001 -1.47174139e-003 X ASA -5.28867555e- 004 X E_stb - 9.64502253e-003 X Kier1 +2.92612997e-002 X Kier2 -9.05227786e-004 X KierA1+2.57936088e-002 X KierA2 +4.04361621e- 002 X SMR_VSA0-2.37125484e-002 X SMR_VSA1 +5.03998977e-002 X SMR_VSA2 +8.13078695e-003 X SlogP_VSA0 - 1.03630885e-002 X SlogP_VSA1 -5.72337043e-002 X SlogP_VSA2 -1.64177905e-003 X SlogP_VSA3 -7.55989243e-002 X SlogP_VSA4 -1.02026342e-002 X SlogP_VSA6 +1.79553609e-001 X a_acc -3.68295238e-002 X a_hyd (Equation 5)

When equation 3 was used to predict the Gibb’s free energy of the test set, it predicted accurately (residual free energy > +1.0) ~86% of the compounds regardless of their structural diversities (Figure 3).

Figure 3: Structures of test compounds showing the experimental and predicted free energies (dG) of binding and residual values (dG_expt --- dG_ predicted).

Given the predictive finesse of this mathematical model, there is a question to be answered and two areas of potential applications to be exploited. Will this model sufficiently predict more chemically diverse compounds? If the yes, then we can predict a more robust interrelationship between statistics and Computer-Aided Drug Discovery in the future. Also, descriptor-based mathematical model screening may be piped as confirmatory steps following structurebased screening for more successful hit-compound identification.

This work was supported by Platform for Drug Discovery, Informatics, and structural life Science from the ministry of Education, Culture, Sports, Science and Technology, Japan.