Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Review Article - (2023)Volume 13, Issue 2
Different values of the Hubble constant for extragalactic objects are not considered here. We give a number of examples of the extreme accordance of expansion rates of different fields of knowledge with the cosmological expansion rate. The coincidence of the expansion rates means that a common cause is almost inevitable. All these examples are gravitationally bound in themselves and in this case are subject to cosmological expansion. According to standard theory, this should not happen. We therefore question the common boundary of gravity and expansion for both theoretical and observational reasons and conclude that all gravitationally dominated objects participate in cosmological expansion or scale drift, contrary to general doctrine. The space expands with its contents while numerically maintaining distance, radius, rotation time and density. What is generally interpreted as an expansion is obviously a scale drift with a drift rate that corresponds to the size of the Hubble constant. The earth is subject to expansion and scale drift. This results in numerically constant measured values. This drift apparently also applies to distant galaxies and other objects. The cosmological red shift is not interpreted here as a Doppler effect and numerical increase in distances, but in accordance with standard theory as an expansion or drift of the space-time scale. The expansion of the radii of galaxies makes the assumption of dark matter superfluous. The continents and our everyday environment are not subject to expansion or scale drift.
Cosmological expansion; Earth expansion; Common expansion rates; Recession velocity; Relative velocity
A number of accordances with the Hubble relation or expansion rate of the universe (72 km× s−1 ×Mpc−1 ≅ 2.4×10−18 s−1 ) were found in areas connected by gravity. A causal connection was already ruled out by Einstein, et al. [1]. This was certainly a reason to ignore the counter-arguments, some of which lay in areas of knowledge other than astrophysics. However, there are reasons not to do so. Therefore, some relevant terms will be explained in particular. These terms are described in more detail in sections 2-4. Section 5 briefly describes the origin and nature of counter-arguments and section 6 contains some resulting conclusions. Basic conclusions on which others build are: Cosmological expansion is also present in areas dominated or defined by gravity. Cosmological expansion does not correspond to a relative velocity according to Special Relativity (STR). We therefore assume that cosmological expansion does not lead to a relative velocity and therefore to no change in the number of distance units. However, there is an expansion of these units, i.e. a scale drift. These expanding units include spatial as well as temporal units. Today’s SI second was smaller in the past and identical to the UT-1 second. With this drift, any distance defined by gravity expands.
In the spectra of extragalactic objects, redshift values occur which correspond to a recession velocity greater than the speed of light (c).The cosmological recession velocity cannot therefore be a relative velocity in the sense of Special Relativity (STR) [2]. Numerical changes in distances (relative velocities) are therefore different from cosmological recession velocities. The numerical distance only changes if there is a relative velocity. Relative velocities between light source and observer corresponding to the STR are therefore ruled out as the cause of the cosmological redshift, provided peculiar velocities are neglected.
The expansion of the universe or space is therefore not a numerical increase in the growing distances in space. The distances and radii expand with space, so they do not expand into space. This leads to the unusual situation that the distances increase but not the number of distance units. The distance units are subject to the same rate of expansion as the distances. We therefore assume: Not the number of distance units, but their scale value expands or drifts. The space expands with its objects while numerically maintaining distance, radius, rotation time and density. A numerical increase of the distance or relative velocity according to STR therefore does not exist due to cosmological expansion. With the expansion of space, the numerical distance does not change, but space with its dimensions expands (Mpc, light year, AU, kilometre, second etc.). The expansion of space with the Hubble parameter means that 1 Mpc has grown about 72 km after one second [3]. An object at a distance of 1 Mpc does not move away with a relative velocity of 72 km/s, but with this recession velocity. The numerical distance of an object after any time remains constant 1 Mpc and the expansion corresponds to an enlargement (drift) of the unit of measurement Mpc.
The lower limit of cosmological expansion or scale drift
The lower limit of cosmological expansion postulated by Einstein, et al. [1], is found today by comparing (differenceformation) the respective potential of a gravitating mass with the potential of cosmological expansion. Here, a substantial incorrectness is committed: The potential of a gravitational mass leads to a change in the relative velocities of objects in the area of influence. In contrast, cosmological expansion does not result in a relative velocity according to STR but something else. So two different phenomena are being compared. Such a comparison is inadmissible. Through this inadmissible comparison, one comes to the assumption: Gravitationally bound objects are not subject to cosmological expansion. We consider this assumption to be incorrect. With a few exceptions [4-7], it is widely agreed that gravitationally bound objects do not expand cosmologically. On the other hand, despite the redshift of the Virgo cluster, i.e., cosmological recession, the so-called Virgo infall exists [8]. Besides this obvious contradiction, expansion effects of the size of the Hubble constant are repeatedly found in much smaller areas. As a result of different assumptions about the lower limit of cosmological expansion, we hold our own view.
The lower limit is not formed by the Einstein, et al. [1], relationship, nor by comparing the potentials of gravitation and expansion. We assume that the lower limit of the cosmological expansion is found by comparing the effects of the gravitational potential with the effects of the electromagnetic potential. If one compares the shape of planets with the shape of small planetoids or even smaller objects, it becomes apparent that the shapes are differently shaped or dominated. Low-mass objects, such as small asteroids, are obviously not influenced in their expansion behaviour and shape by their own gravity. The inner binding is not primarily due to gravity, as is the case with the earth, moon and planets, but due to other forces (electromagnetism). We conclude that the lower expansion limit is in the transition region. With increasing mass, the shapes become rounder and more shaped by gravity. Smaller and lower-mass objects show crystalline and molecular shapes. The shape-forming properties are less or not dominated by gravity. For example, overhanging parts of a construction (bridges, jibs on cranes) do not obey gravity. A 1 m slab of rock does not become a sphere in free space due to its own gravity. The internal electromagnetic forces are stronger than the gravitational forces. Although gravity determines the structure of space, this plays a subordinate role in this case. Consequently, monolithic rigid blocks expand less or not unless they exceed a limiting size/mass ratio. Molecular/ crystalline forces dominate the shape of the rock slab. However, debris piles of the same size can expand. The inner spatial properties determined by gravity are subordinate to the inner electromagnetic properties when the mass is small. Cosmological expansion or scale drift is a property of gravitationally dominated space. This property is not relevant for low mass. Due to this subordination, objects of our daily environment and smaller ones (e.g. small asteroids, seconds pendulums and caesium atoms) do not participate in the cosmological expansion or scale drift. The relation (1) used below loses its meaning. Although the earth as a whole is subject to cosmological scale drift (expansion) according to Wu, et al. [9], this does not apply to continents of a few kilometres in thickness (thickness) (Table 1) [10]. Even small asteroids obviously do not expand. The acceleration of rotation for small asteroids can therefore occur not only through a change in mass or YORP effect, but also through shrinkage with numerically constant radius and angular momentum. The seconds pendulum does not expand like the earth’s radius, the moon’s orbit or the distance and size of extragalactic objects. The spatial and temporal size of the light-second (299,792.458 km) therefore gradually becomes smaller (shorter) compared to these “units of measurement”, despite numerical constancy. Because small objects are not gravitationally dominated, they shrink compared to gravitationally dominated objects at constant angular momentum. The system of measurement with the SI second shrinks compared to the UT second [11]. The distance between the earth and the Moon is determined by gravity and is subject to expansion. The expansion concerns-as with the earth’s radius-the size of the units of measurement, not their number.
| Row | Example | Rate | Possible other causes | References |
|---|---|---|---|---|
| 1 | Expansion-rate of the universe | 2.33 ± 0.26 × 10-18 s-1 | - | [3] |
| 2 | Expansion of galaxies | 2.37 × 10-18 s-1 | ? | [12,13] |
| 3 | Pioneer anomaly | 2.91 ± 0.44 × 10-18 s-1 | Thermal radiation pressure | [19,20] |
| 4 | Expansion of moon’s orbit (LLR-technology) | 3.15 ± 0.06 × 10-18 s-1 | Tidal friction | [15] |
| 5 | Expansion of moon’s orbit ( Eclipse ) | 2.32 × 10-18 s-1 | Tidal friction | [14,16] |
| 6 | Delay of the earth’s rotation | 2.93 × 10-18 s-1 | Tidal friction | [11] |
| 7 | Distribution of rotational delay of pulsars | 2.7 ± 0.4 × 10-18 s-1 | ? | [18] |
| 8 | Surface relation oceans/continents | 3.3 × 10-18 s-1 | ? | [10] |
| 9 | 5-dimensional field theory | 3.6 × 10-18 s-1 | Scale effect | [19] |
| 10 | Polar diameter of earth | 2.5 ± 0.95 × 10-18 s-1 | Post glacial uplift | [16] |
| 11 | Inner earth’s core | 3.0 × 10-18 s-1 | Growth by phase-conversion | [17] |
| 12 | Expansion of the orbit of Saturn’s moon titan | 2.93 ± 0,52 × 10-18 s-1 | Tidal friction on Saturn | [21] |
| 13 | Origin drift CM ITRF2008+GRACE+OMCT | 2.5 ± 1.0 × 10-18 s-1 | Network sparseness | [9] |
| 14 | Expansion of galaxies | 2.33 ± 0.26 × 10-18 s-1 | DM in Bose-Einstein condensate | [13] |
Table 1: Table represents the rate and other possible causes.
Objects or phenomena bound by their own gravity are listed in Table 1. According to standard theory, these should not show any cosmological expansion.
Coincidences
Random numerical equality of two different phenomena in 1810 and the same dimension are very rare coincidences. The occurrence of such a rare coincidence becomes even rarer when another phenomenon of the same size and dimension is added. The probability or better improbability is then to be exponentiated. The coincident rates from terrestrial tidal friction (rotational deceleration) and cosmological expansion rate are a coincidence of two different phenomena. A coincidental coincidence of this coincidence with the delay rate from the Pioneer anomaly is already an almost impossible coincidence. As other phenomena (Table 1) are added, we exclude coincidental accordance and assume causal accordance. The phenomena mentioned have a common rate because they have a common cause. This cannot be tidal friction. Causal accordance cannot be based in the earth’s sphere because, for example, even the most distant galaxies are obviously subject to this rate of expansion (Table 1) [12,13]. As the cause of this common rate we see the still unknown cause of cosmological expansion or scale drift. However, their lower limit then lies in the area in which gravity is dominant over other basic forces, i.e., in the area of gravitationally bound objects.
Measured values versus standard theory
The occurrence of the rate ̴ 3 × 10-18 s-1 in all ranges mentioned in Table 1 from the earth’s radius to the astronomical horizon is remarkable. In these two extreme cases, relative velocities are excluded as the cause of the existing rate. For the earth’s radius, the exclusion is due to measurement results by Wu, et al. [9], and for the universe because recession velocities at large distances are greater than the speed of light (v>c). If there is a common cause, the relative velocities are also to be rejected for intermediate values. This is true for lunar orbit and solar orbit in the galaxy, among others. If no relative velocities occur as a result of cosmological expansion, the corresponding distances are numerically constant despite this expansion. The cosmological expansion manifests itself as recession speed or scale drift. For the distance of the earth’s radius it is approx. 0.05 cm/a [10]. For the lunar orbit, the result is approx. 2.9 cm to 3.9 cm/a, depending on the type of measurement [14-16]. The distance of the solar orbit in the galaxy results in a recession velocity of about 4 × 1015 km/orbit (̴ 420 Ly/orbit) or 18 × 106 km/a and for the Andromeda Nebula it is about 50 km/s. However, the recession velocity of the Andromeda Nebula is superimposed by a larger, opposite relative velocity. The values given are obtained by using the rate α=2.5 × 10-18 s-1 and relation (1). The values obtained from this agree with the measured values (if measurable).
α=Δr/(t × r) ……………. (1)
(α=expansion rate ≡ recession rate, Δr=distance difference or recession value, t=period, r=distance)
The value α ≅ 2.5 × 10-18 s-1 is found several times in the solar system, but also in other gravity-bound systems. α should not be confused with the cosmological scaling factor α. Below are some examples of the occurrence of the cosmological expansion rate in gravitationally bound objects. Further examples are partly included in Table 1.
Inner core of the earth: In 1962, Runcorn [17], gave a growth rate of 243 km/109 years for the inner core of the earth. That is 0.0125 cm per year and radius of the earth’s inner core. With relation (1), this results in an expansion rate or drift rate of ̴ 3 × 10-18 s-1 and thus approximately the cosmological expansion rate or Hubble constant. The “surface” of the inner core of the earth moves away from the centre of the earth proportionally to the surface of the earth, the distance to the Moon and the extragalactic objects because the same rate is present for all of them. More recent publications mostly also assume an expanding inner core of the earth of the same order of magnitude.
Earth radius: Wu, et al. [9], investigate the expansion behaviour of the earth. Among other things, the relative velocity between the centre of mass and the earth’s surface was measured. It was concluded that there was serious evidence of expansion of the earth’s radius. However, the measurements using ITRF 2008+Grace+OMCT+ECCO showed maximum values ̴ 0.1 mm/a or smaller, i.e., insignificant or non-existent at present. Here the found scale drift or origin drift is of interest. Their size is not particularly certain due to insufficient data and, depending on the parameters used, amounts to approx. 0.5 mm/year for the earth’s radius. We set the corresponding values equal and get : 0.05 cm/(31.56 × 106 s × 6370 × 105 cm)=2.5 × 10-18 s-1.
The cosmological expansion rate and the scale drift rate of the earth have the same value.
The deceleration rate of the earth’s rotation is of approximately the same value. According to section 6, other authors [6,18], and we assume tidal friction to be only part of the cause of the rotational lag. The rotational deceleration should lead to the pirouette effect if the earth mass is approximately constant and the moment of inertia is valid. The earth’s radius should expand according to the rotational deceleration. The radius difference (Δr) results as (2).
Δr=r[(1+Δt/t)0.5-1] ……………. (2)
(Δr=radius difference (cm), r=earth radius (cm), t=rotation time (s), Δt=Length of Day (LoD) change(s/100 a)
Δr=6371 × 105[(1+0.0016/86400 )0.5-1 ]=5.9 cm/cy=0.059 cm/a.
The value 0.0016/86400 refers to the lengthening of the day per 100 years.
The value of the radius difference corresponds to the cosmological expansion rate. An expansion of the numerical earth radius is therefore not present according to section 2. This fact was confirmed in 2011 [9]. The increase of the value by 0.059 cm/ (a × r) results from the scale drift at numerically constant earth radius published in 2011 [9]. The value of scale drift of approx. 0.5 mm/year given by Wu, et al. [9], is therefore acceptable. If it is a continuous drift, smaller drift values are obtained for smaller distances and periods and larger drift values for larger distances and periods. The expansion of the lunar orbit and other distances can also be explained by scale drift.
Area ratio continents/oceans: Including the continental shelves in oceanic shelf areas down to a depth of ̴ 200 m, the total continental area on earth is approx. 177 × 106 km2. This area would cover a globe of 3750 km radius almost without a gap. With a radius of r=6370 km, 333 × 106 km2 remain for the oceanic crust. The difference in the radii is Δr=2620 km. The age of the oceanic crust is less than 200 × 106 years, while the age of the continents is about 4 × 109 years (t=1.26 × 1017 s). Using relation (1) with the above values for r, t and Δr, the result for the earth is an expansion rate of α=3.265 × 10-18 s-1.
For comparison: If we assume the age of the continental crust to be 4 × 109 years and the age of the world to be 13.7 × 109 years, this is 29.2%. Since a relatively constant expansion rate of the universe can be expected for 4 ×109 years, a cosmological expansion of 29.2% has occurred during this period. If this is true for the earth according to section 5.2, the earth was 29.2% smaller when continental crust was formed than it is today. The earth’s radius was 1860 km smaller at that time. According to today’s scale, r=6370-1860=4510 km. Relation (1) yields an expansion rate or drift rate of α=2.313 × 10-18 s-1. The difference to the value of α=3.265 × 10-18 s-1 determined above may be due to incorrect crust age or area ratio but also to scale drift. The expansion rate obtained is close to the cosmological expansion rate for both methods.
Lunar distance: The distance to the moon is about 60 times greater than the radius of the earth. The drift value or recession value is 60 times greater than expected for the earth’s radius. The scale drift is then ≈ 3 cm per year and orbital radius of the moon. With relation (1) and the cosmological expansion rate α (2.4 × 10-18 s-1) one obtains the recession value or drift value Δr ≈ 2.9 cm/a. This is in agreement with the drift value of the earth’s radius and the values measured during solar eclipses [9]. Sediment data also indicate an expansion or drift of 2.9 ± 0.6 cm/year [14]. Measurements with LLR give the larger value 3.82 ± 0.07 cm/a (3.15 × 10-18 s-1). However, it is likely that a relative velocity (e.g. from tidal friction) and the recession velocity or scale drift complement each other because the moon still exists (section 6). This assumption is now supported by various authors [7]. In the case of the Andromeda Nebula, a (negative) relative velocity must also be added to the recessional velocity.
Pioneer anomaly: The Pioneer anomaly describes an anomalous delay of the Pioneer X and XI space probes. The delay value is 8.74 × 10-8 cm/s2 [19]. It results from a frequency shift of the radio signals assuming the Doppler effect. Dividing the deceleration value by the speed of light yields a deceleration rate of 2.91 × 10-18 s-1. This value agrees exactly with the earth’s rotational deceleration and corresponds approximately to the Hubble parameter. Shortly after the discovery of the pioneer anomaly, cosmological expansion was considered a possible cause. This possibility was rejected by cosmology [20]. The argumentation: Cosmological expansion only leads to redshift and also only outside gravitationally bound systems. We contradict these assumptions in sections 2 and 3. If, contrary to standard theory, the universe is also expanding in the solar system, the units of measurement of space (metre, light year, second etc.) were smaller at the time of the probe launches than they are today. Due to the expanded units of measurement since the launch of the probes, the current measured distance is numerically smaller than expected. This manifests itself as a delay and a blue shift. With a numerically constant speed of light, the second was also shorter in the past. The time scale corresponds to the course of UT time defined by gravity. This deviates secularly from the electromagnetically defined SI time at a rate of 2.91 × 10-18 s-1.
Orbital expansion of Saturn’s moon titan: Measurements by the Cassini spacecraft show that the orbit of Saturn’s moon Titan is expanding (or drifting) by 11.3 ± 2.0 cm/year. This value could be caused by tidal friction. However, without additional assumptions as described by Lainey, et al. [21], this value is clearly too large for normal tidal friction. However, according to Stephenson, et al. [18], the orbital expansion of our earth’s moon and other Saturnian moons measured by LLR is also too large to be caused by tidal friction. Taking into account the measured value and titan’s orbital radius of 1.22 × 1011 cm, the expansion rate is α=11.3 cm × (31.56 × 106 s × 1.22 × 1011 cm)-1=2.93 × 10- 18 s-1. It should be noted that the closeness to the cosmological expansion rate has already caused discussion [5].
Size evolution of galaxies: The effective radius of large galaxies decreases with increasing distance and the inner density and dynamics increase. There are a number of studies on this subject [12,13,22]. Dokkum, et al. [12], describe galaxies located at a distance of z ̴ 2.2 (̴ 10.7 × 109 Ly). We see these galaxies as they were after 20% of the present world age. The radii are apparently about 0.9 kpc, i.e., 20% of the usual radius of galaxies of the same type and mass today. Such galaxies do not exist in today’s nearby universe. An explanation other than expansion does not seem possible. Let us assume that today’s galaxies began at this size and density. In this case, the expansion rate results from the difference of the radius per radius and the expansion time (1).
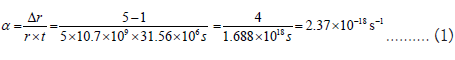
α=required expansion rate, Δr=difference between present radius (5) and emission radius (1), r=adequate present radius (5), t=distance in light time (SI-s).
This expansion rate corresponds to a Hubble constant of 73.2 (km/s)/Mpc. The objects are gravitationally bound objects. They expand according to the cosmological expansion. This contradicts standard cosmology. Trujillo, [22], makes a similar observation when he writes: “Consequently, the very dense nature of our objects at high z could reflect the much denser state of the universe at the time of their formation”. We see that these studied objects exhibit the same effect and rate of expansion as observed today as scale drift on earth (earth radius).
1. According to paragraph 2, a relative velocity does not exist due to cosmological recession. Orbiting objects thus maintain their numerical distance from the centre of gravity despite this recession. The orbital speed and orbital radius of the earth remain numerically constant despite the expansion (recession) of about 11 m × a-1 × AU-1, as does the length of the year. With the numerically constant orbital radius, the orbital velocity also remains numerically constant despite recession. This is true for lunar and planetary orbits as well as for stars in galaxies. In the diagram (orbital radius versus orbital velocity), the level of the orbital velocity is approximately flat towards the outside. The flat course of the orbital velocities in galaxies [23] does not require dark matter. Modified Newtonian Dynamics (MOND) is also not required.
2. The earth and the orbits of other gravitationally bound objects expand according to scale drift rate. However, the numerical radii remain constant, since relative velocities according to section 2 do not exist [9].
3. The Moon moves away from the earth at approximately the same recession rate as by Hubble constant. We conclude that the measured recession is primarily not a relative velocity. The measured value of the lunar recessions is about 3.8 cm/a. 2.9 cm/a of this obviously refers to the cosmological expansion or scale drift of the units of measurement. A relative velocity of 2.9 cm/a, i.e., a change in the numerical distance, therefore does not exist (analogous to the earth’s radius) [9]. Only the difference of 3.8-2.9=0.9 cm/a can be a relative velocity. This value corresponds better than the other two values to the expected tidal friction and requires no destruction of the moon by the earth’s Roche limit at early times.
4. According to section 5.7 it can be assumed that radii and distances of spiral galaxies used to be smaller during cosmic expansion, but were numerically constant according to section 2. In the process, the outer regions of the galaxies move away from their centre faster than the regions near the centre. We observe an analogous situation with distance measurements of the earth’s radius and the moon’s orbit in relation to the earth’s centre of inertia at different times.
5. The continents and our everyday environment do not participate in the expansion or scale drift. These objects as well as e.g. small moons and planetoids are obviously dominated and shaped by electromagnetic forces and not by gravity (section 3).
6. The lower limit of the cosmic expansion is not removed. However, it is at a smaller distance than in the standard theory. The size of this distance is interesting for space travel (pioneer anomaly), geophysics (LoD), time determination (leap seconds) and other fields. This makes this value interesting for space travel (pioneer anomaly), geophysics (LoD), time determination (leap seconds) and other fields.
Using the brightness of supernovae, it was found that the Hubble constant was smaller at great distances (in space or time) than it is today. The cosmological recession velocity or scale drift has increased less per Mpc at great distances than in the near universe (there<70 km × s-1 × Mpc-1). According to section 2, gravitationally defined dimensions (radii, distances, time periods) are subject to expansion or scale drift. The Hubble constant relates a recession velocity (km × s-1) to a distance (Mpc). This also applies to long distances. The lower recession speed per Mpc there refers to the smaller Mpc there. The expansion rates thus remain approximately the same here as there (≅ 2.4 × 10-18 s-1). This contradicts the increase in the Hubble constant due to dark energy.
The deceleration rate of the earth’s rotation is of close size to the expansion rate of the universe. The delay corresponds to a drift of the (SI) time scale. Since time and space have approximately the same scale drift rate (≅ 2.5 × 10-18 s-1), the numerical constancy of the speed of light is ensured. The galaxies mentioned in section 5.7 have a distance of about 10.7 × 109 Ly according to the current scale value. Since this distance is numerically constant according to section 2 and had smaller scale values at the beginning, the number of spatial and temporal distance units results in (3).
∑=0.5n(x1+xn) ……………. (3)
(∑=Sum of the past distance units since emission, n=number of distance units defined today, x1=scale value of the first unit after emission (=1), xn=scale value of the unit in the observation (=5)).
The light that reached us was therefore not 10.7 × 109 years but 32.1 × 109 years on the way. If one observes objects whose distance is close to the world age, the light travel time is close to ∞.
The value of the cosmological recession can be calculated with relation (1). For the distance earth-sun (AU), this results in a recession value of approx. 11 m × a-1 × AU-1. According to section 2, this recession velocity is not a relative velocity and as such does not exist in the sense of the STR. Wu, et al. [9], find that a relevant relative velocity of the distance earth centre-surface (earth radius) does not exist either. However, a scale drift corresponding to the expected recession speed was measured for the earth ( ̴ 0.5 mm × a-1 × r-1). This drift rate corresponds to the cosmological expansion rate.
The recession value of the AU of 0.15 m × a-1 × AU-1, determined is obviously a recession value of the AU of 0.15 m × a-1 × AU-1 is obviously a relative velocity with a cause other than cosmological expansion. A decrease in the mass of the sun, for example, results in a low relative velocity of the increasing distance earth-sun (AU).
Objects bound by their own gravity are subject to cosmological expansion (scale drift), contrary to standard theory. This is not the case for other objects. The former include massive objects such as fixed stars, pulsars, earth, galaxy clusters. Other objects include, for example, smaller, low-mass planetoids and moons (<200 km), continents and objects in our environment.
Hilgenberg, Carey, Scalera and many others assume that the earth is expanding. It seems that this assumption is partially justified. NASA confirm this assumption by stating: The measured number of units of the earth’s radius remains almost constant. However, the size of these units expands according to scale drift rate.
[Crossref] [Google Scholar] [PubMed]
Citation: Müller V (2023) Cosmological Expansion Rate-Various Measurement Results and Interpretation. J Phys Chem Biophys. 13:345.
Received: 14-Mar-2023, Manuscript No. JPCB-23-22180; Editor assigned: 17-Mar-2023, Pre QC No. JPCB-23-22180 (PQ); Reviewed: 31-Mar-2023, QC No. JPCB-23-22180; Revised: 07-Apr-2023, Manuscript No. JPCB-23-22180 (R); Published: 14-Apr-2023 , DOI: 10.35248/2161-0398.23.13.345
Copyright: © 2023 Müller V. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.