Shock wave-vortex interaction that is generated in external flows and internal flows (inlets, nozzles, and combustors) is a complex and often unsteady phenomenon. For analyzing external flow around supersonic aircraft with wings of large sweep and small aspect ratio this classical problem in theoretical gas dynamics is very important. Generation of a vortex sheet near the leading edge of the wing and its subsequent rolling into two isolated vortices is the important feature of such flows. These vortices interact with shock waves formed on the aircraft surface elements. Two isolated vortices are usually formed in the flow around a delta wing at subsonic speeds at some incidence angles [1,2]. These vortex structures can enter the engine inlet of a supersonic aircraft. The flow-rate, drag, and other parameters of this propulsion element significantly depend on the interaction mode of the vortex and the shock wave that always formed ahead of a supersonic inlet engine. Such situations can lead to problems for a supersonic aircraft. The vortex can interacts with the aircraft surface in supersonic external flow, which significantly alters the lifting and moment characteristics of wings and other aircraft elements. Loss of stability and controllability of the aircraft is the result of changes in the force characteristics.

One of the usages of interaction of a vortex with a shock wave can also arise in the study of fuel and oxidizer mixing in combustion chambers of hypersonic flying vehicles with air-breathing engines [3]. In such vehicles, there is supersonic flow regime in the combustor causing complications in fuel and oxidizer mixing.

The experimental and numerical works on shock-vortex interactions are extensively presented by a number of researchers. Gnani et al. [4] have studied shock diffraction around sharp and curved splitters at Mach speeds of 1.31 and 1.59 using Schlieren photography. Their study suggests that the flow field evolves more rapidly with stronger structures for the higher incoming Mach number. Quinn et al. [5] have made some measurements of global pressure filed generated by shock wave diffraction using paints for their CFD validations at two Mach numbers of 1.28 and 1.55. They concluded that the strong interaction at Mach number 1.55 observed numerically may not supported by their experimental observations. Sun and Takayama [6] have made a numerical simulation of laminar flows of vortical structures in shock diffraction and explained factors responsible for the deviation of laminar solutions from experimental results. Chatterjee [7] has numerically studied shock wave deformation in shock-vortex interaction. He has introduced a simple model to explain shock structure formation and its dependence on the strengths of the interacting vortex and shock wave. Ellzey et al. [8] have performed a computational study based on a High Resolution Shock Capturing scheme of the interaction of a planar shock wave with a cylindrical vortex. They observed a severe reorganization of the flow field and acoustic levels in the downstream region reflected mainly due to the strength of shock wave. Abate and Shyy [9] have studied the dynamic of a normal shock wave within a tube leading to vortical flows. Their calculations identified a multiple physical mechanisms included shock–strain rate interaction, baroclinic effect, vorticity generation, and different aspects of viscous dissipation as observed experimentally. Zare-Behtash and Kontis [10] have conducted experimental study to examine the interaction of shocks and vortices with a two-dimensional ejector. The incident shock Mach numbers of 1.34, 1.54, and 1.66, were studied. They concluded that the induced flow is unsteady and dependent on the degree of compressibility of the initial shock wave.

The aim of present study is to model high Mach number shockvortex interactions and to assess robustness of the developed finitevolume TVD scheme for solving compressible flow equations for such complex problems. The other goal is to assess the levels of acoustic pressure at high supersonic Mach numbers of 2.5 and 2.9.

The action of a strong external disturbance on the vortex propagating in the flow results in the so-called vortex explosion or vortex breakdown, as was shown in the experimental works of [11,12]. This phenomenon was observed both in incompressible flows containing vortices and in compressible subsonic and supersonic flows. The meaning of term “vortex explosion” is formation of a point (or a surface) of total stagnation of the flow in the region of interaction of the vortex and the strong disturbance also the formation of a reverse flow region near the vortex centerline. The problem of vortex explosion has not been ultimately solved, even in the case of an incompressible fluid [11]. Various experiments for determining vortex-breakdown conditions were done for an incompressible fluid. Zatoloka et al. [13] were obtained important results in the experiments for supersonic velocities. They assumed that the mechanisms of vortex explosion and boundary-layer separation are similar. This idea was developed by Glotov [14]. Origination of unsteady oscillatory regimes in the region of interaction of the vortex and the shock wave was observed in [14,15]. Quantitative experimental results were obtained in [12,16]. Vortex-core radius, intensity of vortex and free-stream Mach number was used as parameters determining the interaction mode, and data on the structure of interaction regimes were obtained. In addition to the information given above, investigations [1] show formation of supersonic vortices on the back side of a delta wing and in the wake behind a complex-shaped body. Supersonic circular components of velocity and a wake-type vortex were studied experimentally [12,16].

If the vortex intersects the shock wave, two interactions types are possible: 1) interaction of the vortex with the shock wave perpendicular to the vortex axis; 2) interaction of the vortex with the shock wave inclined to the vortex axis. The first type of interaction was experimentally studied in [12,15,16], and the second type was considered in [14,17]. It was shown in these works that, in the first case of interaction, the vortex break down, and a reverse flow region with flow unsteadiness appears. There are a few numerical works in high supersonic where the interaction of the vortex and the shock wave is very strong causing numerical instabilities. Some vortex-shock wave interaction regimes with vortex explosion were observed in some works [18,19], whereas no vortex breakdown was obtained in other works [20]. Therefore, it is necessary to develop a mathematical model for predicting experimentally generated vortices in a complex (often unsteady) flow types such as interaction of a vortex with an oblique shock wave. There is little works to study on interaction of a vortex with an oblique shock wave and its reflection. Zhang et al. [21] has studied an oblique shock wave interaction with two vortices at sonic to slightly supersonic flows. Mahesh [22] has also reported an analytical model on the onset of vortex breakdown for several cases.

The objective of the present work is numerical simulation of various types of interaction of a vortex with an oblique shock wave (and its reflection from surface) by means of unsteady two-dimensional Euler equations. A mathematical model of the vortex is developed. Calculation results of interaction of the vortex with oblique shock waves are presented.

A supersonic perfect-gas flow is considered with a vortex entering to the flow at some upstream position. The velocities in the vortex core and in the cocurrent flow are assumed to be supersonic. An oblique shock wave is inclined at a certain angle to the path of the vortex. This shock hits a flat surface representing a flyer surface at supersonic flows and reflects so as to generate a weaker reflected shock wave. To simplify problem formulation, we assume that the shock-wave generator is outside the computational domain (Figure 1). Direction of the vortex is parallel to the direction of horizontal inflow. The intensity of the vortex is characterized by vortex circulation Γ₀ and the vortex-core radius R_C are the vortex governing parameters. The values of Γ₀ and R_C are prescribed to the flow and then left to interact with the flow and the oblique shock waves. In determining properties on the shock wave, it is assumed that the angle of the wedge generating the shock wave is prescribed, and thus, the angle of inclination of the shock wave generated is known. The flow properties at the upper boundary are specified from the property relations for oblique shock wave. A reflective wall boundary condition and an outflow boundary condition implemented [23].

Figure 1: Schematic of an oblique shock wave and a vortex.

Glotov [14] has shown that the beginning of vortex-core breakdown on the shock wave is independent of viscosity and is mainly determined by the relative component of velocity in the vortex core and by the angle of inclination of the shock wave. Therefore, the inviscid ideal-gas flow is assumed and the unsteady Euler equations are solved numerically in this work. The effects of viscosity is little on the interaction zone and the main features of the flow structure can be obtained by implementing a more proper vortex model which is introduced in this study.

Vortex model

It is necessary to construct a mathematical model of the vortex to investigate interaction of the vortex and shock waves. It is desirable to have a vortex insulated from the external cocurrent flow (at least in the initial step). The structure of a vortex formed behind a diamondshaped body exposed to a supersonic flow was experimentally studied in [15,16]. The results showed that the structure of the vortex being formed is close to the structure of the Burgers vortex. In the present work, the Burgers vortex model is used that satisfy experimental dependences of the velocity in the vortex center on the vortex radius and flow velocity at infinity [12]. The distribution of quantities across the vortex is similar to the distribution of properties in the classical Burgers vortex; a linear distribution of velocity is set in the vortex core and velocity decreases exponentially with distance from the vortex core. The tangential velocity V_θ in the Burgers vortex is written as

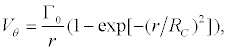(1)

where Γ₀ is the vortex circulation and R_C is the vortex-core radius. The velocity components u and v in Cartesian coordinate system (x,y) may be expressed as

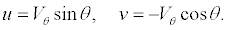(2)

The pressure distribution in the vortex is calculated from the conservation of momentum in radial direction expressed by

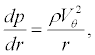(3)

where the radial component of velocity is assumed to be zero. In calculating density in the vortex, it was assumed that the total temperatures in the vortex and in the cocurrent flow are identical. This assumption is confirmed by the experimental data of [12], which show that the ratio of total temperatures in the vortex and in the cocurrent flow is within 0.95-1.05. The differential equation (3) for the pressure across the vortex is then simplified using equation (1) and assuming H₀ = H_0∞ = constant , i.e. the total enthalpy to be constant, leads to [23]

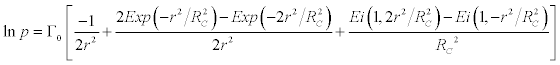(4)

where Ei(a, z) is the Exponential integral of the arguments inside and it can be expressed by

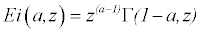(5)

where Γ is the Gamma function.

Figure 2 shows the distributions of pressure and tangential velocity along the radius of the vortex modeled by the differential equation derived above. The calculations were performed with the following parameters: 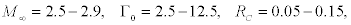and ratio of specific heats γ =1.4.

Figure 2: Distributions of (a) pressure and (b) tangential component of velocity across the vortex.

In Figure 2, the pressure is normalized to γM²_∞ , the velocity V_e to the velocity of sound in the flow at infinity, and r to the size of the computational domain along the y axis (equal to 1.0 m). It follows from Figure 2 that the tangential component of velocity increases with increasing radius, reaches a maximum at the vortex-core boundary, and then exponentially decreases. The static pressure in the vortex core changes significantly weaker and is approximately 10% lower than the pressure in the ambient flow.

Table 1 summarizes and compares experimentally generated vortices with the present analytical results with the maximum error bound of 6.9% for the maximum angular Mach number.

Property	Experiment [12]	Present	Error (%)
	5.5	5.5	0.0
	1.64	1.643	0.183
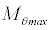	0.58	0.62	6.9
	0.41	0.411	0.24

Table 1: The characteristics of experimental vortex compared with present analytical solution.

The governing euler equations

The equations of fluid flow without viscous forces, body forces, heat conduction or energy sources are referred to as the Euler equations. The Euler equations in two-dimensional Cartesian coordinates and in conservation-law form can be written as

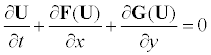(6)

where

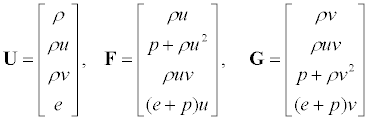(7)

The primitive variables are the density ρ, the velocity components u and v, and the pressure p. The total energy per unit volume e, is related to p by,

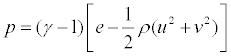(8)

where γ is the ratio of specific heats (γ =1.4 for air).

Acoustic field

For spherical sonic waves, the sound intensity is given by:

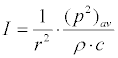(9)

where ρ is the density of the medium, c is the sound speed, and ( p² )_av is the square of mean sonic pressure for r=1. Sound intensity level (SIL) is generally used to express acoustic filed in decibel as

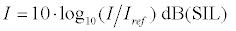(10)

Numerical TVD algorithm

A total variation diminishing (TVD) method was introduced by Harten [24,25] and later generalized by Yee [26-28] for solving compressible fluid flows. This is a class of finite-difference high resolution shock capturing technique for discretising and solving the governing fluid flow equations in conservation law forms.

The TVD approach is then modified to be of finite-volume type by Sedaghat [29,30]. In this approach, the governing equation (6) is integrated over a finite-volume ABCD as follows:

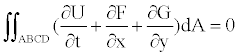(11)

By implementing the Green theorem, one may arrive at:

(12)

Where s is a unit vector along any faces of a control volume ABCD and n is a unit vector normal to the faces, as shown in Figure 3.

Figure 3: Schematic of a finite-volume (ABCD) in two dimensions.

The vector H= (F,G) represents the fluxes in (8) and is expressed in two dimensional flows by

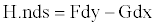(13)

The governing fluid flow equation (12) then can be approximated as

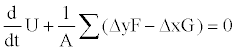(14)

where is discretized as

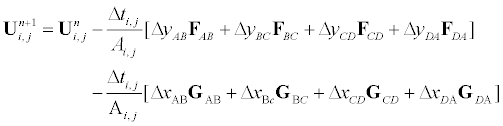(15)

Where A_i,j is the area of the quadrilateral ABCD, and expressions for some of terms in (15) may be given as

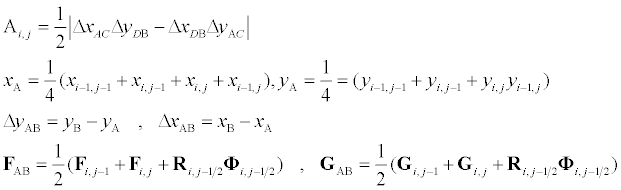(16)

More expressions can be obtained similarly for the rest of terms in equation (16). The TVD terms associated with represents numerical nonlinear artificial viscosity terms to maintain numerical stability when solving Euler equations. Derivation of this term and the corresponding symmetric and upwind limiter functions are expressed in detail in Sedaghat [29,30].

Numerical simulation of the flow structure in the case of interaction of a vortex with an oblique shock wave was performed for a range of free-stream Mach numbers M_∞= 2.5 − 2.9 . It was assumed that the stream wise direction of the vortex axis is parallel to the direction of the x axis. It was also assumed that the direction of the flow velocity vector ahead of the shock-wave front coincides with the direction of the x axis. The variable properties were the circulation Γ₀ and vortexcore radius R_C . The computations were performed for the following geometric dimensions of the domain: length of 4.1 m and width of 1.0 m. The geometric definition of the incoming vortex was also assumed to be unchanged. The experimental and numerical investigations of vortex-shock wave interaction show that a drastic increase along the vortex (vortex breakdown) in the region of its interaction with the shock wave depends mainly on velocity deficit. Depending on velocity deficit, the interaction structure was essentially different. Our computational results revealed two modes of interaction of the vortex with shock waves (weak and strong) depending on the combination of the governing properties M_∞, Γ₀ , R_C.

Weak interaction

Figure 4 shows a typical example of the weak mode of interaction of the vortex and an oblique shock wave. The flow structure is shown in this figure. The computation was performed for the following flow parameters: 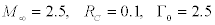. The angle of the wedge generating the shock wave is 10.94°. It follows from Figure 4 that the vortex passes through the shock wave and, interacting with the reflected one from the wall surface, turns at a certain angle; the axis of symmetry of the vortex becomes parallel to the velocity vector behind the shock wave (actually, the vortex propagates along the wedge generating the shock wave). It is found that the vortex remains almost undistorted when passing through the shock wave. The vortex shape behind the shock-wave front changes weakly and is close to a circle. The shockwave shape does not change significantly either. The slope of the shock wave also remains almost unchanged. As a result of weak interaction, the flow in the entire computational domain remains supersonic. Thus, weak interaction is characterized by weak distortion of the shock-wave front, minimum change in the vortex structure, and supersonic velocity in the entire flow region. The flow structure is unchanged in time. This agrees with the experimental data of [12], which also show that the flow structure in the case of weak interaction remains unchanged in time.

Figure 4: Isolines of pressure in the case of weak interaction

Strong interaction

In this case, extreme changes in the shock-wave shape and properties of the incoming vortex ahead of the shock wave, especially behind the reflected shock are observed. Because of the low values of the total pressure, Mach number in the vortex core, and angle of inclination of the velocity vector to the shock wave, the shock-wave front and the flow structure in the interaction region ahead of the front become substantially different. Figure 5 shows the flow structure in the case of strong interaction of the vortex with the shock wave for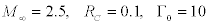

Figure 5: Contours of pressure in the case of strong interaction

In this case, the vortex breakdown does not occur but the vortex oscillates and constitutes two counter rotating vortices which again combined to make a single vortex as shown in Figure 6. This was also experimentally observed [12].

Figure 6: Core vortex division into two counter rotating vortices in the case of strong interaction

Figure 7 shows the flow structure in the case of strong interaction of the vortex with the shock wave leading to vortex breakdown for the case 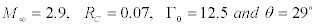. In this case, extreme changes in the shock-wave shape and properties of the incoming vortex ahead of the shock wave, especially behind the reflected shock are observed. Because of the low values of the total pressure, Mach number in the vortex core, and angle of inclination of the velocity vector to the shock wave, the shock-wave front and the flow structure in the interaction region ahead of the front become substantially different as sketched in Figure 8. In the case of strong interaction, the shape of the shock-wave front in the interference region differs from the straight line. A local zone of subsonic recirculation flow is formed, which is located upstream of the initial position of the shock-wave front at a certain distance depending on the governing properties.

Figure 7: Contours of pressure in the case of strong interaction

Figure 8: Shock wave-vortex flow structure in the interaction region in the case of strong interaction

Recirculation flow regions are visible ahead of the main shock wave and its reflection in Figure 9. It follows from the computation results that the flow in these regions is subsonic. A shock wave is formed around the recirculation region. In the case of interaction of the vortex and the shock wave, there is a closed subsonic recirculation flow region near the centerline of vortex. Between the normal shock and recirculation region, there is a point with zero flow velocity at the vortex centerline. The angle of inclination of the shock wave formed around the recirculation flow region to the vortex axis is variable, since the Mach number in the vortex core increases significantly in the direction away from its axis (at the centerline, the shock-wave front is perpendicular to the vortex axis). With distance from the centerline, the slope of the shock-wave front decreases.

Figure 9: Recirculation subsonic region ahead of shock wave during strong interaction.

Thus, in the case of strong interaction, there arises a subsonic reverse flow region ahead of the front of the main shock wave. In its structure, this region is similar to the separated flow region arising, for instance, in the viscous supersonic flow around a compression corner. The emergence of the reverse flow region leads to significant expansion of the vortex cross section. In all examined regimes of strong interaction, a subsonic reverse flow region was observed, which was separated from the supersonic flow region by a slip surface over the entire perimeter. The size of the reverse flow region depends on the shock-wave strength, i.e., on the angle of the wedge generating the shock wave. The length of the local subsonic flow region can serve, to a certain extent, as a characteristic of the strong interaction mode. Similar to weak interaction, rarefaction regions appear behind the shock wave in the case of strong interaction. This leads to a decrease in pressure on the wedge surface as compared to the pressure arising in a uniform supersonic flow around the wedge; this decrease is more significant in the case of strong interaction. Thus, the pressure on the wedge in the case of strong interaction is lower than that in the case of weak interaction.

The following features of the flow structure behind the recirculation flow region can be noted. One can see the forming of the Mach structure and Mach and Regular reflection structure in Figure 9. The presence of two vortices is confirmed by a significant decrease in density in them and by the change in the direction of the velocity vector over the vortex perimeter. The vortices rotate in the opposite directions. With increasing x coordinate (i.e., with distance from the shock-wave front), the area occupied by the subsonic flow in the vortex decreases.

The results of the weak shock wave–vortex interaction (M=2.5) and the strong interaction (M=2.9) are compared in terms of Sound Intensity Level (SIL) in decibel in Figure 10 for different values of vortex strength (Γ) which shows higher acoustic strength at higher Mach number.

Figure 10: Sound intensity levels for the two cases of weak and strong interaction.

In Figure 10, we see the effect of vortex strength Γ₀ and the Mach number on the acoustic field of a vortex interaction with an oblique shock wave. The computational results show that vortex strength become less effective compared with Mach number at higher vortex strength. At higher vortex intensities, the sound intensity levels remain nearly unchanged.

The numerical result of the interaction of a vortex with an oblique shock wave is presented here. A mathematical model of the vortex is introduced which describes vortices generated experimentally. Two types of interaction, namely weak and strong are identified. It is shown that vortex breakdown is possible in the case of strong interaction. The effect of vortex breakdown is characterized by a significant change in its structure: a subsonic recirculation region appears and the vortex diameter substantially increases. It is also demonstrated that the intensity and the size of vortex may be responsible for destabilizing effects when is hit by an oblique shock wave. It is observed that at smaller vortex intensities, the free stream Mach number may play a crucial role on the sound intensity levels.