International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2018) Volume 9, Issue 1
Quarter-circle Break Water (QBW) is a modified semi-circular breakwater, which are similar to caisson consists of a quarter circular surface facing incident waves, with horizontal bottom and a rear vertical wall and are generally placed on a rubble mound foundation. QBW may be constructed as emerged with and without perforations that may be one side or on either sides. By these perforations, the energy is dissipated owing to the formation of eddies and turbulence is created inside the hollow chamber. In this paper, the data collected from the experimental work carried out at National Institute of Technology, Surathkal is analysed by plotting the non-dimensional graphs of reflection coefficient, reflected wave height and incident wave height for various values of wave steepness. These values are used for prediction of QBW adopting Artificial Neural Network (ANN) and Regression (REG) approaches. In ANN, Multi-Layer Perceptron (MLP) and Radial Basis Function networks are considered for training the network data. Goodness-of-Fit (GoF) test viz., Kolmogorov-Smirnov test statistic and Model Performance Analysis (MPA) viz., correlation coefficient, mean absolute error and model efficiency are applied for checking the adequacy of ANN and REG approaches to the observed data. The results of GoF test and MPA indicates the MLP is better suited for evaluation of hydrodynamic performance of QBW.
<Keywords: Auto-regression; Correlation coefficient; Kolmogorov-Smirnov test; Model efficiency; Multi-Layer perceptron; Radial basis function; Mean absolute error
Breakwater is a structure generally, used in coastal protection works and also for creating tranquillity in basin in harbours. Over the year’s breakwater were of rubble mound weighing in tons. In the latter part of 19th century innovative structures like tetrapods, tripods and other interlocking blocks are also evolved. Considering the huge quantity of rock material required, in the beginning of 21st century caisson type of breakwater were thought off. One such breakwater is Quarter-circular Break Water (QBW), a new-type breakwater first proposed by Xie et al. [1] on the basis of Semi-circular Break Water (SBW). The QBW is usually placed on rubble mound foundation and its superstructure consists of a quarter circular surface facing sea sides, a horizontal bottom and a rear vertical wall. The QBW structure is hollow, hence, the weight and materials required are less and it is more suitable where the foundation is relatively weak. The QBW is a prefabricated caisson, which can be properly designed for handling stresses and can be transported and placed with more precision at the desired location. Depending upon the purpose the QBW may be fabricated as emerged type structure, with and without perforation to dissipate the incident wave energy.
Jiang et al. studied the performance of QBW by comparing the hydraulic performances of QBW and SBW under similar hydraulic conditions [2]. They conducted 2-dimensional (2D) vertical wave numerical model and physical model studies, and found that wave reflection of both QBW and SBW are closer to each other. They stated that the wave reflection coefficient (Kr) remains almost same with values less than 1.0 even when free board (hc) value becomes 2 to 3 times incident wave height (Hi) for both types of breakwaters. During wave overtopping in submerged condition, they found high flow velocity and vortexes near the rear walls of QBW, which may be due to top sharp corner and sudden expansion of flow around QBW. They described that the flow fields in front of both QBW and SBW are similar in both in submerged as well as emerged conditions and this explains the closeness of reflection coefficient (Kr) values for both breakwaters.
Shi et al. studied the hydrodynamic performance of QBW under both regular and irregular wave conditions [3]. Regular waves were generated by reciprocating wave paddle at constant speed whereas irregular waves were generated by frequency spectrum simulation with target spectrum of JONSWAP type. For analysing the wave reflection, two types of wave reflection coefficients were described by Shao viz., (i) Kr that describes the whole effect of wave reflection by breakwater and (ii) Circular-surface reflection coefficient (Krc) that describes the reflective effect by circular surface on the adjacent flow field in front of the breakwater [4]. He found that at the same relative freeboard height (hc/Hi), the value of Kr was higher than Krc that indicates the entire reflective effect of QBW is stronger than that by circular surface on the adjacent flow field. To estimate the energy dissipation as the wave passes over the breakwater wave energy loss parameter (KEloss) was described. KEloss is the ratio of dissipated wave energy to the original gross wave energy within the process of wave structure interaction. Based on the results obtained from the study, it was found that the loss of wave energy for emerged breakwater is larger than that for submerged breakwater.
Hegde and Ravikiran conducted experiments on physical model of QBW in 2D wave flumes to evaluate the reflection characteristics of QBW of different radii in different submergence conditions [5]. The models were made of galvanized iron sheets and coated with cement slurry to simulate concrete surface. For finding the variation of Kr different graphs were plotted with the incident wave steepness (Hi/gT2) (where, g is the gravitation and T is the wave period) for various submergence ratios (d/hc) and different ranges of (R/Hi) (where, d is the depth of water and R is the breakwater radius). For all values of d/hc and R/Hi, they found that Kr increases logarithmically (best-fit) as incident wave steepness increases. The study revealed that whatever may be the depth, caisson radius, height of structure crest (from sea bed) steeper the waves the more will be the reflection from breakwater. Hafeeda conducted experiments in a 2D monochromatic wave flume on a seaside perforated QBW model [6]. He analyzed the experimental data by plotting the non-dimensional graphs of Kr (i.e., Hr/Hi) (where, Hr is the reflected wave height) for various values of R/Hi. He observed that the value of Kr increased with increase in wave steepness and when the free board (hc) increased then the value of Kr also increased. He found that when height of the structure (hs) increases, smaller height of the QBW portion of the caisson is exposed to waves, which is effect of the curvature is less pronounced that tend to lesser dissipation and more reflection.
Binumol et al. conducted physical model studies of QBW with three different radii and S/D (spacing to diameter of perforations) ratio [7]. Dimensional analysis was carried out to find the non-dimensional parameters such as incident wave steepness, depth parameter (d/gT2), height of structure, depth of water, wave run up (Ru/Hi), wave rundown (Rd/Hi), etc., using Buckingham’s π-theorem. The experimental data collected was analyzed by plotting the graph of dimensionless wave run up and dimensionless wave rundown for various values of wave steepness and different height of structure to the depth of water. They observed that the value of Ru/Hi increases with increase in wave steepness for all values of hs/d and d/gT2. This was because as wave height increases there is increase in wave energy and hence run up increases with increase in wave steepness. For all values of hs/d and d/gT2, the dimensionless wave rundown was found to decrease with increase in wave steepness for all values of hs/d and d/gT2 because as wave height increases there is increase in wave energy resulting in more run up and hence less rundown. Rd/Hi was also found to increase with the increase in the depth parameter (d/gT2) because at higher water depths, effect of curvature is more pronounced resulting in lower run up and hence more wave rundown.
Balakrishna and Hegde investigated reflection coefficient (Kr) and dissipation (or loss) coefficient (KL) for physical models of quarter circle caisson breakwater for different radii with constant S/D ratio [8]. They observed that reflection coefficient was found to increase with wave steepness, which was similar to all earlier studies. Dissipation coefficient (KL) decreased with increase in wave steepness. The study revealed that as wave period decreases the value of loss coefficient decreases. The study also revealed that as hs/d increases, dissipation increases which is a reverse trend in the case of reflection, this trend is found to be true for all values of d/gT2 values.
Generally, computational intelligence techniques viz., Artificial Neural Network (ANN), adoptive neuro fuzzy interface system, support vector machine regression, genetic algorithm, etc., have been efficaciously proposed as an efficient tool for modelling and predictions in coastal engineering problems [9]. In the present study, ANN and Regression (REG) approaches are used for prediction of the variables considered for evaluation of hydrodynamic performance of QBW. In ANN, Multi-Layer Perceptron (MLP) and Radial Basis Function (RBF) networks are adopted for training the network data. Goodnessof- Fit (GoF) test viz., Kolmogorov-Smirnov test statistic and Model Performance Analysis (MPA) viz., correlation coefficient, mean absolute error and model efficiency are applied for checking the adequacy of ANN and REG approaches to the observed (or experimental) data. This paper presents the study on evaluation of hydrodynamic performance of QBW using ANN and REG approaches with illustrative example.
ANN modelling procedures adapt to complexity of input-output patterns and accuracy goes on increasing as more and more data become available. Figure 1 shows the architecture of ANN that consists of input layer, hidden layer, and output layer [10].
From ANN structure, it can be easily understood that input units receive data from external sources to the network and send them to the hidden units, in turn, the hidden units send and receive data only from other units in the network, and output units receive and produce data generated by the network, which goes out of the system. In this process, a typical problem is to estimate the output as a function of the input. This unknown function may be approximated by a superposition of certain activation functions such as tangent, sigmoid, polynomial, and sinusoid in ANN. A common threshold function used in ANN is the sigmoid function (f(S)) expressed by Eq. (1), which provides an output in the range of 0 ≤ f(S) ≤ 1.
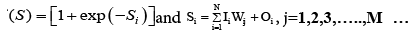 (1)
(1)
Where, Si is the characteristic function of ith layer, Ii is the input (I) value of ith layer, Oi is the output (O) value of ith layer, Wij is the synaptic weights between input layer (i) and hidden layer (j), N is the number of observations and M is the number of neurons (or units) of hidden layer [11].
Theoretical description of MLP network
MLP network is based on architecture with single hidden layer as shown in Figure 1. Gradient descent is the most commonly used training algorithm in MLP in which each input unit of the training data set is passed through the network from the input layer to output layer [12]. The network output is compared with the target output and output error (E) is computed using Eq. (2).
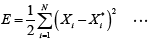 (2)
(2)
Where, Xi is the observed value of ith sample and 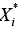 is the predicted value for ith sample.
is the predicted value for ith sample.
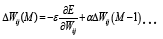 (3)
(3)
Where, ΔWij(M) is the weight increments between ith and jth layers during M neurons (or units) and ΔWij(M-1) is the weight increments between ith and jth layers during M-1 neurons (or units). In MLP, momentum factor (α) is used to speed up training in very flat region of the error surface to prevent oscillation in the weight and learning rate (ε) is used to increase the chance of avoiding the training process being trapped in local minima instead of global minima.
Theoretical description of RBF network
RBF network is supervised and three-layered feed forward neural network. The hidden layer of RBF network consists of a number of nodes and a parameter vector called a ‘centre’, which can be considered the weight vector. In RBF, the standard Euclidean distance is used to measure the distance of an input vector from the centre. The design of neural networks is a curve-fitting problem in a high dimensional space in RBF [11]. Training the RBF network implies finding the set of basis nodes and weights. Therefore, the learning process is to find the best fit to the training data. The transfer function of the nodes is governed by nonlinear functions that is assumed to be an approximation of the influence that data points have at the centre. The transfer function of a RBF is mostly built up of Gaussian rather than sigmoid. The Gaussian function decrease with distance from the centre. The transfer function of the nodes is governed by nonlinear functions that is assumed to be an approximation of the influence that data points have at the centre. The Euclidean length is represented by rj that measures the radial distance between the datum vector 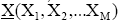 and the radial centre
and the radial centre 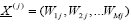 can be written as:
can be written as:
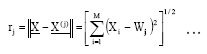 (4)
(4)
Where, 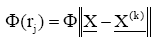 is the Euclidean norm and Φ( ) is the activation function. A suitable transfer function is then applied to rj to give
is the Euclidean norm and Φ( ) is the activation function. A suitable transfer function is then applied to rj to give 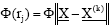 . Finally, the output layer (k-1) receives a weighted linear combination of Φ(rj).
. Finally, the output layer (k-1) receives a weighted linear combination of Φ(rj).
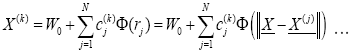 (5)
(5)
Where cj is the centre (c) of the neuron in the hidden layer (j) and Φ (rj) is the response of rj and W0 is the bias term [13].
Theoretical description of regression approach
Number of regression models such as linear regression, auto regressive moving average and auto regressive integrated moving average are generally adopted for evaluation stationary data. In the present study, as the available data is stationary, the basic requirement to develop the regression (REG) model is satisfied and hence used for prediction of the variables. The REG models for prediction of dependant variables (KL, Kr and Kt) using various independent variables are presented in Table 1.
| Sl.No. | Dependant variable | Independentvariable | REG Model |
|---|---|---|---|
| 1 | KL | T, Hi, HT,Hr, Kr, Kt, Hi/d, L, Hc/Hi, Hi/gT2,Hi/gT2 (2) | φ1T+φ2Hi+φ3HT+φ4Hr+φ5Kr+φ6Kt+φ7Hi/d+φ8L+φ9Hc/Hi+φ10Hi/gT2+φ11Hi/gT2(2)+C1 |
| 2 | Kr | T, Hi, HT,Hr, KL, Kt, Hi/d, L, Hc/Hi, Hi/gT2,Hi/gT2 (2) | φ1T+φ2Hi+φ3HT+φ4Hr+φ5KL+φ6Kt+φ7Hi/d+φ8L+φ9Hc/Hi+φ10Hi/gT2+φ11Hi/gT2(2)+C2 |
| 3 | Kt | T, Hi, HT,Hr, KL, Kr, Hi/d, L, Hc/Hi, Hi/gT2,Hi/gT2 (2) | φ1T+φ2Hi+φ3HT+φ4Hr+φ5KL+φ6Kr+φ7Hi/d+φ8L+φ9Hc/Hi+φ10Hi/gT2+φ11Hi/gT2(2)+C3 |
Table 1: Description of REG Model.
In Table 1, the terms Φi (i=1, 2, 3…., 11) are regression coefficients and C1, C2 and C3 are constants.
Goodness-of-Fit test
GoF test involving viz., Kolmogorov-Smirnov (KS) test statistic is applied for checking the adequacy of applying ANN and REG approaches to the series of observed data [14]. Theoretical description of the KS test statistic is as follows:
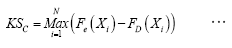 (6)
(6)
Where, Fe(Xi)=(i-0.35)/N is the empirical Cumulative Distribution Function (CDF) of Xi and FD(Xi) is the computed CDF of Xi by ANN and REG approaches.
Model performance analysis
The performance of ANN and REG approaches adopted in prediction of the variables (KL, Kt and Kr) is evaluated by Model Performance Indicators (MPIs) viz., Correlation Coefficient (CC), Mean Absolute Error (MAE) and Model Efficiency (MEF), and are given below:
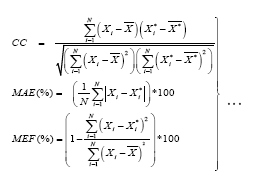 (7)
(7)
Where, 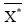 is the average value of observed (or experimental) data and
is the average value of observed (or experimental) data and 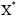 is the average value of predicted data [15]. The model with high CC, less MAE and better MEF is considered as best suited amongst ANN and REG approaches adopted in prediction of the variables used for evaluation of hydrodynamic performance of QBW.
is the average value of predicted data [15]. The model with high CC, less MAE and better MEF is considered as best suited amongst ANN and REG approaches adopted in prediction of the variables used for evaluation of hydrodynamic performance of QBW.
In this paper, a study on comparison of hydrodynamic performance of QBW was carried out. The experimental data viz., depth of water (d), wave period (T), incident wave height (Hi), transmitted wave height (Ht), reflected wave height (Hr), transmission coefficient (Kt), loss coefficient (KL), wave length (L), reflection coefficient (Kr), incident wave steepness (Hi/gT2), relative freeboard (hc/Hi) and relative wave height (Hi/d) collected at National Institute of Technology, Surathkal, is analysed by plotting the non-dimensional graphs of reflection coefficient, reflected wave height and incident wave height for various values of wave steepness. The values were used for prediction of QBW adopting ANN and REG approaches.
Description of experimental setup
The study was conducted in the regular wave flume available in the marine structures laboratory of the Department of Applied Mechanics and Hydraulics, National Institute of Technology Karnataka, Surathkal. The experiments were performed in wave flume with dimensions of 50 m long, 0.74 m wide and 1.1 m deep. Out of 50 m, 42 m length has smooth concrete bed. It has a 6.3 m long, 1.5 m wide and 1.4 m deep chamber at one end, where, wave flap is hinged at the bottom generates waves. The flap is controlled by an induction motor of 11 kw, 1450 rpm and is regulated by an inverter drive, 0 to 50 Hz rotating with a speed range of, 0 to 1550 rpm. This facility is able to generate regular waves of 0.08 to 0.24 m of periods 0.8 to 4 s.
A series of vertical asbestos sheets are spaced at about 10 cm distance from each other and kept parallel to the length of the flume to dissipate the generated waves by damping the disturbance caused by successive reflection and to smoothen them. The QBW model is placed in the flume 28 m away from the wave flap, above the rubble mound foundation (Figure 2). The slope used for the rubble foundation is 1:2. Three capacitance type wave probes were used for measuring the incident and reflected wave heights. The wave probes were placed at a distance of 4 m from the centre of the model.
The determined optimum network architecture with model parameters obtained from MLP and RBF networks, and regression models was used for prediction of QBW. In ANN (using MLP and RBF networks), 75% of data was used for training (TRG) and 25% of data used for testing (TES) the experimental data. Similarly, in REG, 75% of data was used for calibration (CAL) and 25% of data used for validation (VAL) while developing the REG equations. Statistical software, namely, SPSS (Statistical Package for the Social Sciences) is used to predict the hydrodynamic characteristics viz., KL, Kr and Kt of QBW using ANN and REG approaches. The experimental data was trained with MLP and RBF networks to determine the Optimum Network Architecture (ONA) for the variables viz., KL, Kr and Kt. The determined ONAs with model parameters obtained from MLP and RBF networks, and REG equations were used for prediction of QBW. The results obtained from ANN (using MLP and RBF networks) and REG approaches were presented in Sections 5.1 to 5.3.
Prediction of KL, Kr and Kt using MLP
The momentum factor (α) and learning rate (ε) were fixed as 0.6 and 0.05 while optimizing the network architecture of MLP for KL, Kr and Kt. The network data was trained with ONA (i.e., 11-21-1) with one input layer with 11 units, one hidden layer with 21 hidden units and one output layer with one unit. The network was tested with model parameters for prediction of the variables (KL, Kr and Kt) to evaluate the hydrodynamic performance of QBW.
Prediction of KL, Kr and Kt using RBF
By using the procedures of RBF, as described in Section 3.2, the experimental data was trained with model parameters to determine the ONAs of KL, Kr and Kt. The ONAs were determined as 12-7-1 for KL whereas 12-10-1 for Kr and 12-4-1 for Kt. The ONAs were further used to test the network data of the variables viz., KL, Kr and Kt.
Prediction of KL, Kr and Kt using REG
By using the procedures of REG approach, as described in Sec 3.3, the REG equations for the dependant variable (s) in terms of the independent variables were developed and given as:
KL = (-0.625)T+(-0.022)Hi+(0.021)HT+(0.031)Hr+(-0.690)Kr+(-1.829)Kt+(0.153)Hi/d+(0.266)L+(0.011)Hc/Hi+(-0.022)Hi/gT2+(0.016)Hi/gT2 (2)+2.291
Kr = (-0.396)T+(-0.007)Hi+(0.001)HT+(0.062)Hr+(-0.469)KL+(- 0.767)Kt+(-0.275)Hi/d (0.196)L+(-0.002)Hc/Hi+(0.009)Hi/gT2+(0.081)Hi/gT2 (2) +1.070
Kt = (-0.185)T+(-0.028)Hi+(0.025)HT+(0.011)Hr+(-0.431)KL+(- 0.266)Kr+(0.393)Hi/d (0.076)L+(0.008)Hc/Hi+(0.104)Hi/gT2+(0.104)Hi/gT2 (2) +1.120
Analysis based on GoF test
The KS test statistic values of ANN (using MLP and RBF networks) and REG approaches for the variables KL, Kr and Kt were computed and found to be varied between 0.125 and 0.210. These values were noted to be less than of its theoretical value of 0.221 at 5% level, and at this level, both ANN and REG approaches are found to be acceptable for prediction of the desired variables (KL, Kr and Kt). The predicted variables were used for evaluation of hydrodynamic performance of QBW.
Performance analysis based on MPIs
The model performance of ANN and REG approaches used in prediction of the variables (KL, Kr and Kt) was evaluated by MPIs and the results are presented in Tables 2 and 3.
| Vari-ables | Computed values of MEF and MAE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MEF (%) | MAE (%) | |||||||||||
| MLP | RBF | REG | MLP | RBF | REG | |||||||
| TRG | TES | TRG | TES | CAL | VAL | TRG | TES | TRG | TES | CAL | VAL | |
| KL | 96.3 | 98.8 | 58.8 | 89.9 | 92.6 | 95.8 | 1.6 | 1.2 | 6.8 | 3.5 | 2.6 | 2.3 |
| Kr | 90.9 | 97.7 | 71.7 | 78.7 | 92.0 | 94.6 | 1.6 | 0.9 | 3.0 | 2.7 | 1.7 | 1.5 |
| Kt | 97.3 | 99.5 | 66.7 | 86.2 | 96.5 | 96.7 | 0.9 | 0.5 | 3.7 | 2.7 | 1.2 | 1.5 |
Table 2: Values of MPIs for KL, Kr and Kt given by MLP, RBF and REG.
| Variables | Computed values of CC | |||||
|---|---|---|---|---|---|---|
| MLP | RBF | REG | ||||
| TRG | TES | TRG | TES | CAL | VAL | |
| KL | 0.981 | 0.994 | 0.769 | 0.956 | 0.962 | 0.980 |
| Kr | 0.950 | 0.968 | 0.836 | 0.677 | 0.956 | 0.945 |
| Kt | 0.986 | 0.998 | 0.825 | 0.959 | 0.982 | 0.983 |
Table 3: Values of CC for KL, Kr and Kt given by MLP, RBF and REG.
From Table 2, it could be noticed that the MEF obtained from MLP is relatively higher when compared with the corresponding values of RBF and REG. Also, from Table 2, it could be noticed that the percentage of MAE obtained from MLP is less than the corresponding values of RBF and REG. From Table 3, it may be noted that the CC values obtained from MLP for the predicted variables vary between 0.950 and 0.998. The time series plots of predicted values of the variables (KL, Kr and Kt) using MLP and REG together with observed data are presented in Figures 3-5. The scatter plots of observed and predicted values of the variables with model fit and R2 (coefficient of determination) values are presented in Figures 6-8.
From Figures 3-5, it can be seen that the predicted values of the variables (KL, Kr and Kt) using mlp network gives better performance than rbf and reg during testing period. from Figures 6-8 it can be seen that the r2 values obtained from fitted model using mlp for KL, Kr and Kt variables are 0.970, 0.926 and 0.980, which indicates that there is a perfect fit between the observed and predicted variables.
Analysis based on descriptive statistics
In addition to MPIs, the performance of ANN (using MLP and RBF) and REG approaches adopted in prediction of the variables (KL, Kr and Kt) was analyzed through the descriptive statistics (i.e., Average, Standard Deviation (SD), Coefficient of Variation (CV), Coefficient of Skewness (CS) and Coefficient of Kurtosis (CK)) and the results are presented in Table 4. Based on the GoF test results using KS test statistic and MPA using MPIs, the study suggested that MLP is better suited amongst MLP, RBF and REG models adopted for prediction of the variables viz., KL, Kr and Kt, which are used for evaluation of hydrodynamic performance of QBW.
By using the values of the descriptive statistics of the KL, as given in Table 4, the percentage of variation on the average of predicted value using MLP, with reference to average of observed value, is computed as 0.6% and 0.2% during TRG and TES respectively. For Kr, the values obtained from MLP during TRG and TES are found to be 1.9% and 1.3% respectively. Likewise, for Kt, it may be noted that the percentage of variation on the average of predicted value using MLP, with reference to average of observed value is computed as 0.2% and 0.1% during training and testing.
| Descriptive statistics | Observed | MLP | RBF | REG | ||||
|---|---|---|---|---|---|---|---|---|
| Datapoints (1 to 27) | Datapoints (28 to 36) | TRG | TES | TRG | TES | CAL | VAL | |
| Dissipation (or loss) coefficient (KL) | ||||||||
| Average | 0.519 | 0.609 | 0.516 | 0.608 | 0.515 | 0.611 | 0.522 | 0.596 |
| SD | 0.134 | 0.128 | 0.129 | 0.135 | 0.119 | 0.095 | 0.129 | 0.133 |
| CV (%) | 25.8 | 21.0 | 25.0 | 22.2 | 23.0 | 15.5 | 24.8 | 22.2 |
| CS | -0.205 | -0.789 | -0.033 | -0.651 | -0.113 | -0.852 | 0.068 | -0.918 |
| CK | -1.139 | -1.112 | -1.386 | -1.501 | -1.108 | -1.714 | -1.760 | -1.381 |
| Reflection coefficient (Kr) | ||||||||
| Average | 0.154 | 0.079 | 0.151 | 0.078 | 0.154 | 0.081 | 0.153 | 0.085 |
| SD | 0.070 | 0.046 | 0.066 | 0.045 | 0.054 | 0.023 | 0.064 | 0.050 |
| CV (%) | 45.3 | 57.9 | 43.7 | 57.7 | 34.9 | 28.4 | 41.9 | 58.1 |
| CS | -0.110 | 0.537 | 0.491 | 0.666 | 0.535 | 1.166 | 0.138 | 0.349 |
| CK | 0.049 | -0.430 | -0.297 | 0.693 | -0.104 | 2.177 | -0.284 | 0.017 |
| Transmission coefficient (Kt) | ||||||||
| Average | 0.823 | 0.771 | 0.821 | 0.770 | 0.814 | 0.767 | 0.823 | 0.778 |
| SD | 0.076 | 0.089 | 0.076 | 0.085 | 0.070 | 0.060 | 0.077 | 0.083 |
| CV (%) | 9.3 | 11.5 | 9.3 | 11.0 | 8.6 | 7.8 | 9.4 | 10.7 |
| CS | -0.329 | 0.602 | -0.287 | 0.635 | 0.100 | 0.649 | -0.355 | 0.608 |
| CK | -1.249 | -1.238 | -1.154 | -0.949 | -1.663 | -1.836 | -1.438 | -1.687 |
Table 4: Descriptive statistics of predicated variables (KL, Kr and Kt) by MLP, RBF and REG.
The paper described the procedures involved in prediction of the variables viz., KL, Kr and Kt adopting ANN (using MLP and RBF) and REG approaches. These variables were used for evaluation of hydrodynamic performance of QBW. From the results of data analysis, the following conclusions were drawn from the study:
• Optimum MLP network architecture viz., 11-21-1 was used for training the network. The ONA of MLP with model parameters was used for testing the network data and prediction of variables.
• Regression equations developed through REG approach was used for prediction of the variables.
• KS test results supported the use of ANN and REG approaches used in determining the hydrodynamic characteristics parameters.
• GoF test results using KS test statistic and MPA using MPIs confirmed that the MLP is better suited amongst MLP, RBF and REG models adopted for prediction of the variables viz., KL, Kr and Kt.
• The percentage of MAE obtained from MLP is less than the corresponding values of RBF and REG during training (or calibration) and testing (or validation) for all three predicted variables. While testing the network (i.e, experimental) data, the MAE using MLP for the predicted variables KL, Kr and Kt were computed as 1.2%, 0.9% and 0.5% respectively.
• For KL, the values of CC and MEF given by MLP were computed as 0.994 and 98.8% respectively during testing period. Similarly, the values of CC and MEF were computed as 0.968 and 97.7% for Kr whereas 0.998 and 99.5% for Kt.
• The percentage of variation on the average of predicted value using MLP, with reference to average of observed value, was computed as 0.2% for KL, 1.3% for Kr and 0.1% for Kt while testing the network data.
The author is grateful to Dr. (Mrs.) V.V. Bhosekar, Additional Director and Director In-charge, Central Water and Power Research Station, Pune, for providing research facilities to carry out the study. The author is thankful to Shri N. Ramesh, Research Scholar, National Institute of Technology, Surathkal, for the supply of experimental data used in the study.